充气式再入减速器动态气动载荷与结构特性研究

吴 杰，张 章，侯安平，王立武，王 洁，曹 旭

(1. 北京航空航天大学能源与动力工程学院，北京 100191；2. 北京空间机电研究所中国空间技术研究院航天器无损着陆技术核心专业实验室，北京 100094)

0 引 言

随着航天技术的不断发展，空天往返运输活动也更加频繁，然而传统刚性返回器的装载能力容易受到结构尺寸的限制，导致有效载荷的局限性越来越突出[1-3]。针对这一缺陷，充气式返回技术应运而生，其在发射过程中折叠以占有尽可能小的体积，返回时通过充气使气囊展开并形成气动外形[4-5]。然而区别于刚性结构，柔性结构型面的气动变形问题更加突出：高超声速气动力会导致薄膜结构的大变形，甚至产生结构断裂与解体[6-7]；气动热载荷会使内充压气体剧烈膨胀并超过气囊缝合强度，从而造成柔性结构破坏。因此研究再入过程中气动载荷与结构特性的变化规律，校核危险点并提出优化方案，在充气式再入减速器的设计过程中愈加重要。

针对充气式再入减速器在气动力与气动热作用下的结构特性，国内外学者已开展了一定的研究工作。现有研究中，在气动力的求解上主要通过CFD计算个别高度工况下的气动压力，并采取单向压力加载的方式求解结构应力[8-11]。然而，由于其通过插值来获取其余高度的气动结果，无法获得更为连续的气动载荷与结构特性变化历程，并且单向耦合无法计入结构变形对于下一时刻流场分布的影响。另一方面，现有研究在求解气动热上主要依靠工程算法或CFD得到表面热流分布，再通过热传导方程得到各功能层温度分布[12-15]，然而其未能考虑内充压气体的热膨胀这一重要因素对于热应力的影响。

针对现有研究方法的不足，本文提出了将动态飞行参数加载至CFD边界条件的技术手段，并且在CFD中通过数次迭代求解更为精确的阻力系数，实现飞行动力学与空气动力学之间的双向耦合。同时基于ANSYS建立了考虑内充压气体热效应的流固双向耦合模型，既考虑了结构变形对下一时刻流场的影响，又考虑了内充压气体温度变化对热应力的影响。利用此模型研究了气动力与气动热分别作用下的结构变化规律，并通过改变半锥角和气囊数目，研究结构参数对气动载荷与结构特性的影响。

1 数值方法及验证

1.1 分析流程

为对比气动力与气动热对结构特性的影响，本文将两者进行分层求解，如图1所示。气动力的分析中，将动态飞行参数作为CFD的边界条件，并结合流固双向耦合模型进行求解。其中，通过CFD求出的阻力系数能够对面元积分法得到的初始阻力系数进行反馈修正。

在气动热分析中，将CFD计算得到的气动热作为边界条件依次加载至热力学及动力学模型中，并且将薄膜热变形以及内充压气体的热膨胀都计入热应力的影响因素中。

1.2 几何模型

充气式再入减速器的几何模型选取美国IRVE飞行器[10]，结构如图2所示。七层气囊独立充气以提供刚性，气囊之间通过隔层连接以增加结构强度，蒙皮包裹在气囊外部以形成稳定的气动外形。柔性薄膜材料选择凯夫拉(Kevlar)纤维膜，该材料密度为1440 kg/m3，杨氏模量131 GPa，泊松比0.35。

图2 IRVE结构示意图Fig.2 Schematic diagram of IRVE system

图3展示了充气式再入减速器的结构有限元模型，采用shell 181四节点面单元，网格数10万。图4是流体域网格模型的剖面图，采用混合网格进行划分，总网格800万。

图3 有限元模型Fig.3 Finite element model

图4 CFD模型Fig.4 CFD model

充气式再入减速器通过热防护系统(Thermal protection system, TPS)抵御巨大的热载荷，从外到内分为防热层、绝热层和气密层，分别用以承受热流、隔绝热流和防止气体泄漏，如图5所示。本文采用solid 45单元建立各功能层的热力学模型。

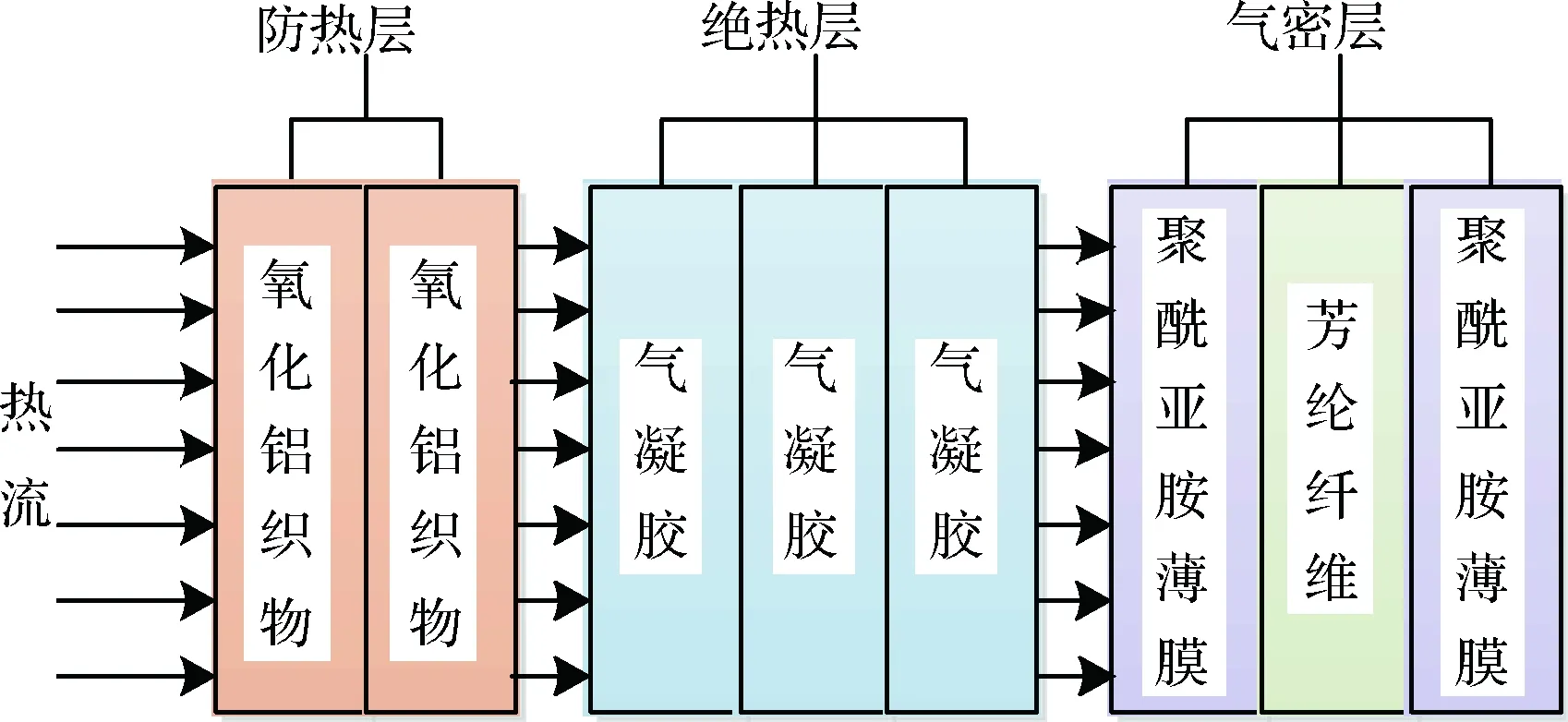
图5 TPS结构示意图Fig.5 Diagram of the thermal protection system

1.3 气动力与气动热计算方法

流体域和固体域通过耦合交界面将位移及压力依据协调条件进行转换。采用基于有限体积法的雷诺平均N-S方程求解气动力，并采用SST湍流模型。在求解气动热时需考虑边界层内高焓气流与结构之间的对流换热，以及壁面产生的辐射。设σ为黑体辐射系数，给定结构发射率ε为0.89，其热辐射方程为：

(1)

利用文献[16]中的CFD结果进行了验证，如图6所示。驻点动压和热流密度的最大偏差均发生在各自峰值处，分别为5.8%和5.1%，均较为合理。

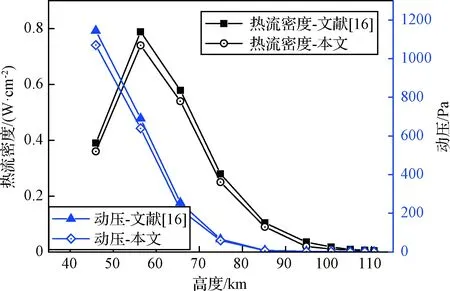
图6 气动力及气动热方法验证Fig.6 Verification of aerodynamic and aeroheating methods

1.4 结构动力学方程

设薄膜厚度为h，其上作用有均匀压力p，此时薄膜将产生横向位移z以及由变形引起的内部张力Tx和Ty。给定弹性模量为E，则静力学控制方程为：

(2)

考虑振动效应，设薄膜单位面积的质量为ms，承受横向压力载荷为f(x,y,t)，则受迫振动方程为：

(3)

文献[17]给出了气囊和隔层上最大应力的理论公式，将本文有限元计算结果和其进行对比，如图7所示。两种方法得到的最大应力都随内压线性增加，但有限元得到的斜率稍大，其偏差均在4%左右。

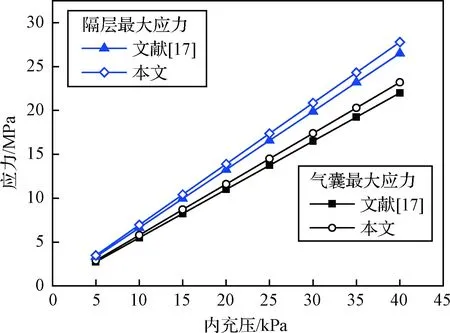
图7 静力学方法验证Fig.7 Verification of static stress method

本文依托北京空间机电研究所回收着陆实验室进行了IRVE试验件的模态振动试验。试验件根据IRVE的结构进行了简化，采取三层气囊的形式，如图8所示。通过锤击法测量试验件在不同充气压力下的模态振型及固有频率。

图8 模态试验件结构Fig.8 Structure of modal test

将试验结果和本文所用方法进行对比，如图9所示，两种方法得到的结果趋势一致。摇摆和横向伸缩频率随内压变化很小，偏差均在9%左右；纵向伸缩频率随内压呈近似线性变化，偏差在7%左右。由于试验件存在销钉、充气阀等连接装置，增加了附加质量，在一定程度上降低了固有频率，因此该偏差在合理范围内。

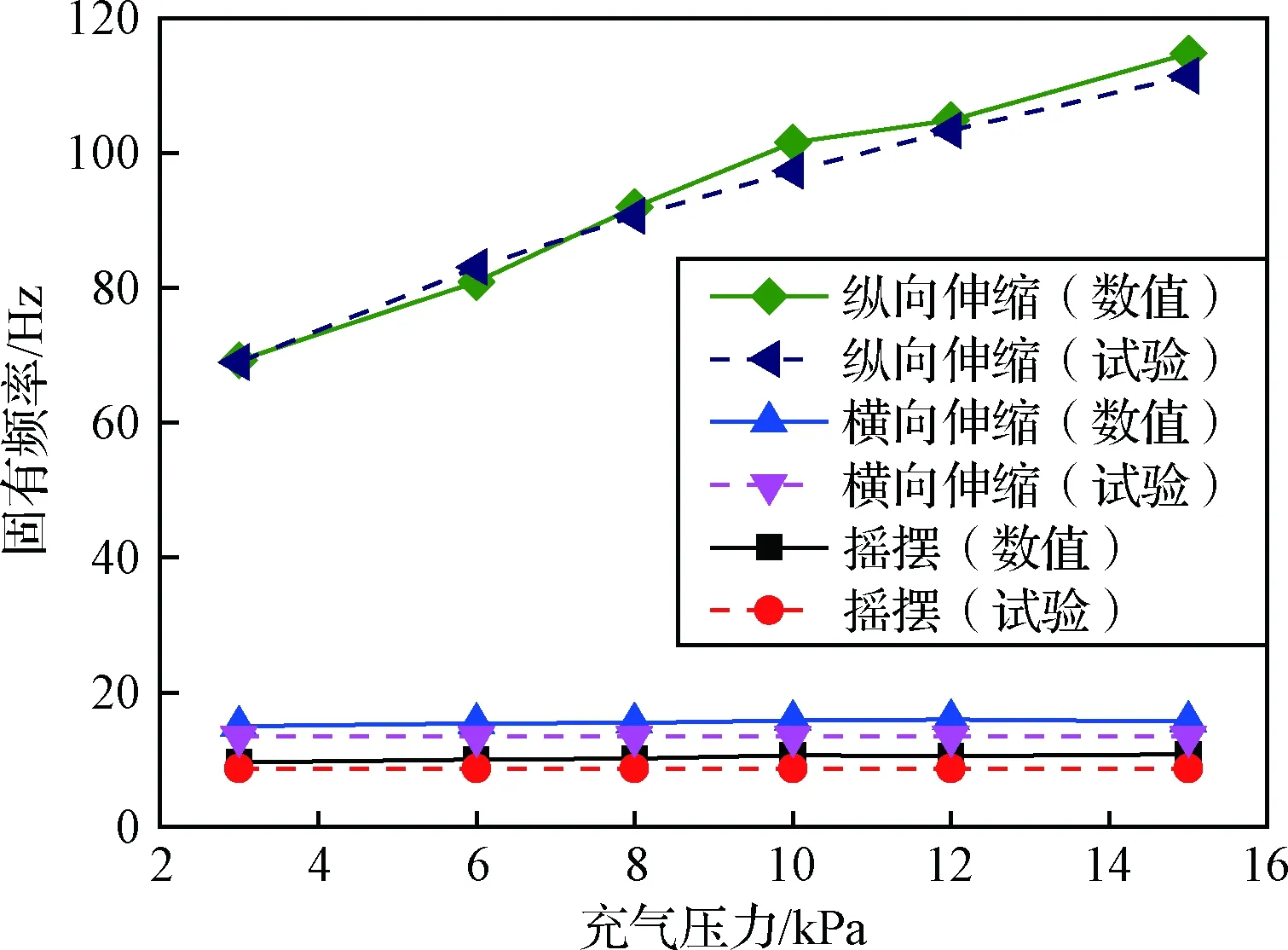
图9 模态方法验证Fig.9 Verification of modal method

1.5 热力学方程

TPS热传导分析的微分方程如下：

(4)

其中,T是温度，c是比热容，λ是热传导率，φ是内热源。对于内充压气体热膨胀，设摩尔质量M，气体常数R，则可通过理想气体状态方程进行描述：

pM=ρRT

(5)

本文根据文献[18]中的参数建立了相应的模型，并和文献结果进行了对比，如图10所示。两者温度曲线基本一致，验证了本文热力学方法的可靠性。

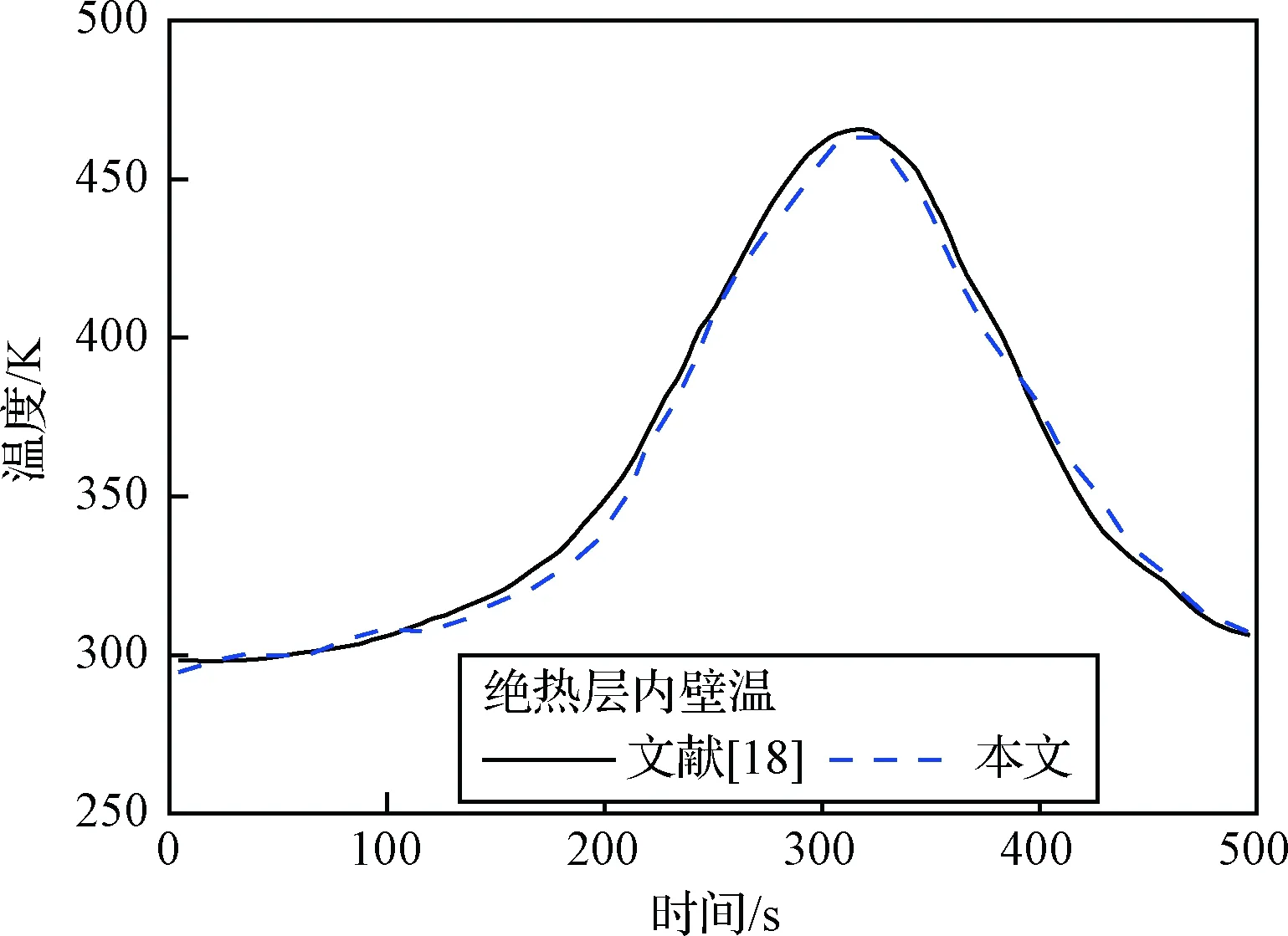
图10 热传导方法验证Fig.10 Verification of heat conduction method

1.6 飞行动力学方程

假设充气式再入减速器以稳定的姿态飞行，无攻角无侧滑，则描述其飞行状态需要六个参数：速度大小v，地心距r，纬度φ，经度θ，弹道倾角γ和飞行方向角Ψ。考虑地球自转，设角速度为w，其三自由度质心运动方程如下所示：

(6)

编写MATLAB程序并和文献[19]给出的算例进行了对比。图11给出了对比结果，由于选用的大气模型存在差异，在再入后半段存在一定偏差，但总体基本吻合，验证了本程序的准确性。

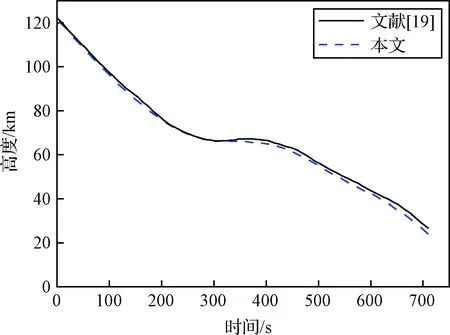
图11 飞行动力学程序验证Fig.11 Verification of flight dynamics program

2 飞行动力学与流场分析

2.1 飞行动力学分析

表1展示了再入过程的初始参数，编写飞行动力学程序并设定时间步长为0.1 s进行迭代求解。

表1 飞行任务相关参数Table 1 Flight parameters

图12展示了高度、速度随时间的变化关系。再入总时间为712 s，其中前180 s为高超声速区，在244 s时进入亚声速区，此时高度降低至32 km。

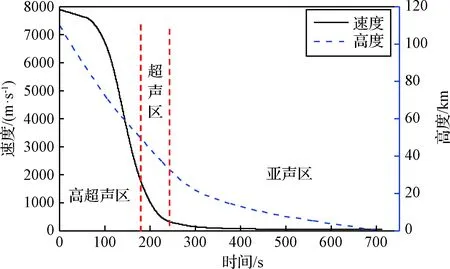
图12 高度及速度曲线图Fig.12 Height and velocity curves

2.2 流场分析

由于亚声速时过载及热流密度都较低，因此本文只针对超声速及高超声速区进行流固耦合分析，结果如图13所示。驻点压力峰值位于60 km高度，大小为5033 Pa；驻点温度峰值位置有所区别，位于66 km高度处，大小为1942 K。

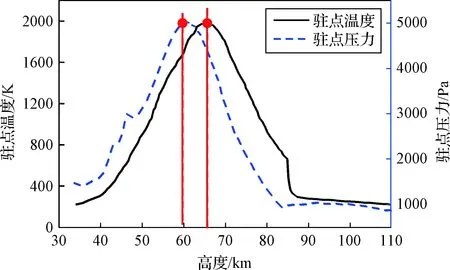
图13 驻点压力与温度曲线图Fig.13 Pressure and temperature curves on stagnation point

选取有代表性的Ma5和Ma1.2进行流场对比，图14是子午面温度云图。Ma5飞行时结构前缘形成一道强烈的弓形激波，到达驻点时温度从240 K升高至730 K，除前缘处气动温度较高外，在飞行器尾部凹陷区亦会产生严重的气动加热。相比而言，Ma1.2飞行时激波曲率更小，脱体距离更大，到达驻点时温度仅升高至326 K。但气流经过迎风面两侧时产生更明显的膨胀波，温度迅速降低至200 K。

图14 流场温度云图对比Fig.14 Temperature comparison of flow field

图15是流场子午面速度云图,Ma5时前缘来流速度从1602 m/s起迅速降低，动能转化为气动热，飞行器尾部凹陷处产生了明显的低速区。相比而言，Ma1.2时由于迎风面两侧产生了更明显的膨胀波，速度升高明显并迅速超过来流速度，达到500 m/s。

图15 流场速度云图对比Fig.15 Velocity comparison of flow field

图16分别展示了表面压力和温度在各自峰值处(60 km与66 km)的分布，图17是两者沿子午线的变化。发现从驻点向周围变化的过程中，温度和压力的下降速度逐渐增加。到达迎风面边缘时，温度从1942 K下降至1169 K，压力从5033 Pa下降至2518 Pa。从背风面来看，温度仍然保持在较高的水平，最大达到1390 K，而压力却仅有230 Pa左右，因此背风面上的气动压力作用可忽略不计。

图16 迎风面压力与温度分布Fig.16 Pressure and temperature distribution on upward

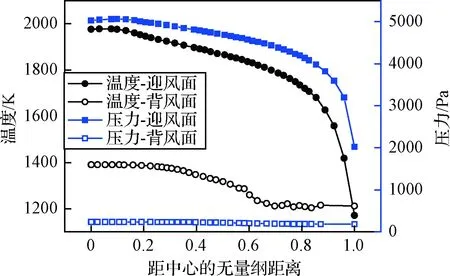
图17 子午线压力及温度分布Fig.17 Distribution of meridian pressure and temperature

3 考虑气动力作用的结构动力学分析

图18展示了气动力作用下的最大应力变化，此时不考虑气动热的影响。其规律和驻点压力相似，在60 km处存在峰值，大小为39.6 MPa。和再入初期相比，最大应力值提升了1.84倍。下文着重选取应力峰值点A研究气动力对应力的影响。

图19对比了无气动力和气动力最大状态(A点)的应力云图。图19(a)中应力完全由20 kPa内充压产生，此时气囊应力普遍高于蒙皮，最大应力位于最内层气囊与隔层连接处，大小为13.9 MPa，超过内压三个数量级。图19(b)中在气动力的作用下，最大应力位于迎风面靠近内层的一圈蒙皮上，大小为39.6 MPa。

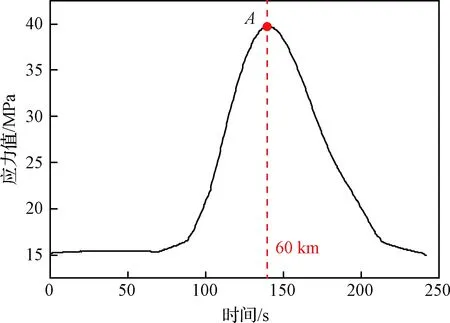
图18 气动力作用下结构最大应力变化Fig.18 Maximal stress variation under aerodynamic

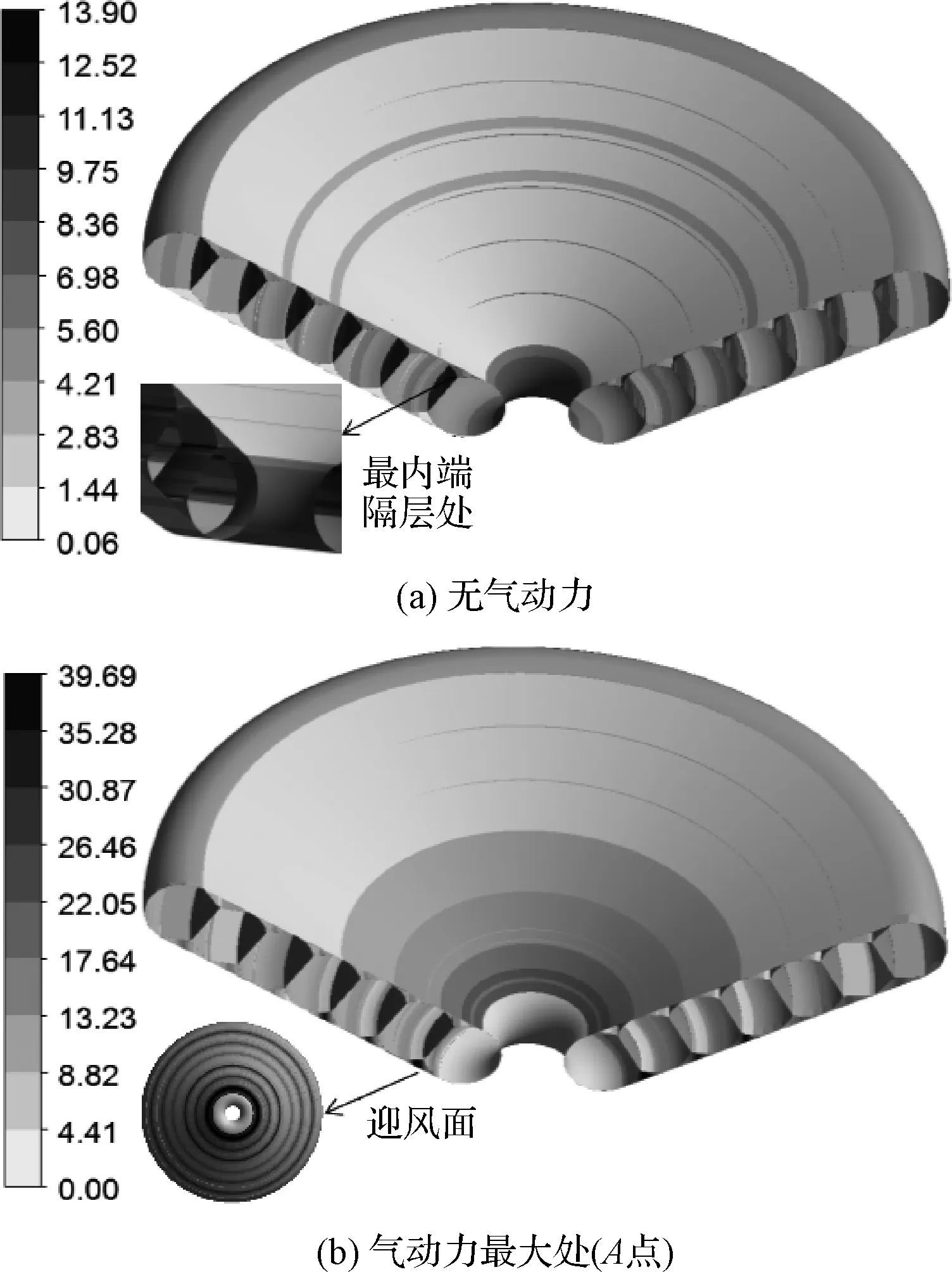
图19 结构应力分布对比Fig.19 Comparison of stress distribution

图20为结构子午面变形云图的对比。图20(a)中结构最大变形发生在各气囊处，其幅值为4.9 mm。

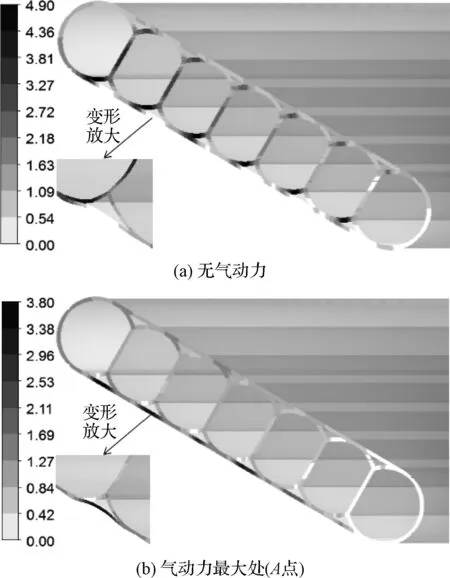
图20 结构子午面变形Fig.20 Meridian deformation of structure

气囊在蒙皮束缚位置会将部分力传递给蒙皮，从而改善自身受力效果。图20(b)中蒙皮受气动力向内部凹陷，最大变形为3.8 mm，在束缚位置会将部分压力传递给气囊，从而改善蒙皮受力。

为比较结构中各位置应力的大小，将蒙皮、气囊和隔层划分成30个部分，如图21所示，通过提取各个面上最大应力，研究不同工况下应力的分布。

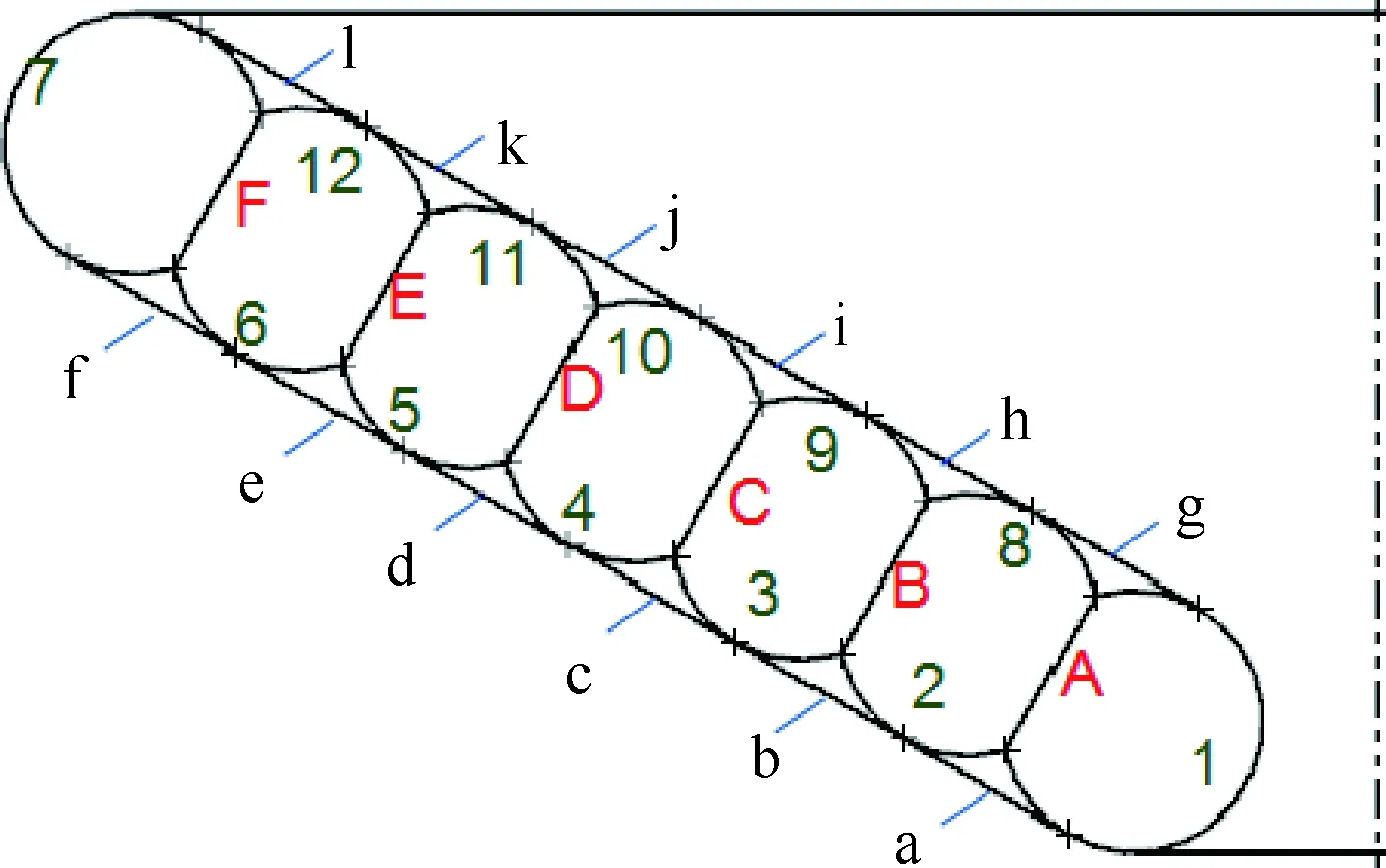
图21 结构标注示意图Fig.21 Structural labeling sketch

图22是气动力作用前后各位置应力的对比，图22(a)中隔层应力最高，气囊次之，蒙皮应力最低。图22(b)中蒙皮最大应力由3.6 MPa突增至39.6 MPa，气囊最大应力也有小幅提升，由11.6 MPa提升至16.8 MPa，仅隔层最大应力有所下降，但幅度很小，从13.9 MPa下降至12.8 MPa。因此内充压对隔层应力的影响最大，而气动力对蒙皮上的应力影响最大。

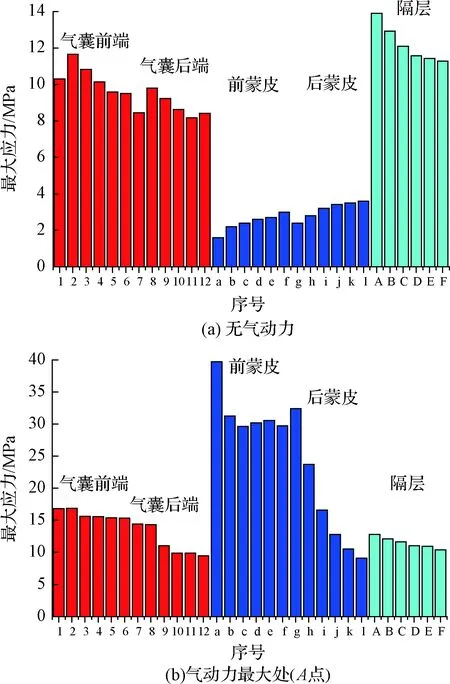
图22 结构各部分应力幅值对比Fig.22 Comparison of stress in different parts

研究内充压作用下的固有振动特性，如图23和表2所示。可以看出，前两阶固有频率一致，为17.132 Hz，对应摇摆振型，表明此振型在X和Y两个方向都有体现；第三阶为伸缩振型，频率为56.488 Hz。

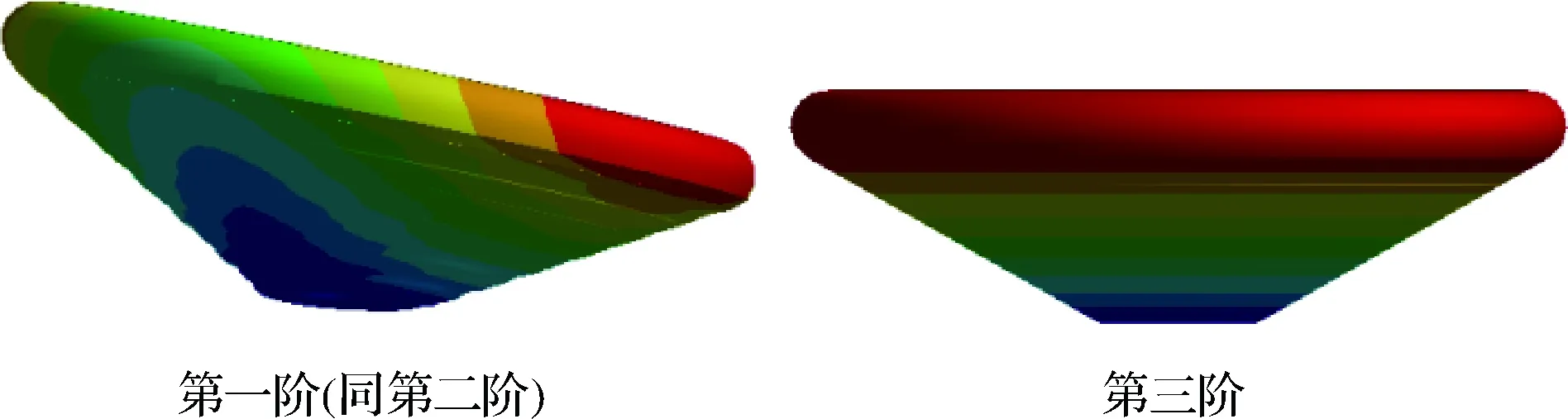
图23 前三阶模态振型Fig.23 The first three modes

表2 前三阶固有频率Table 2 The first three natural frequencies

图24展示了考虑气动力时一阶固频的变化。飞行前半段气动力不断增大，一阶固频逐渐从17.5 Hz下降至14.1 Hz。分析该现象的原因，气动力会削弱内充压气体的作用，从而减小了隔层的拉应力和结构的刚度，进而减小了固有频率。

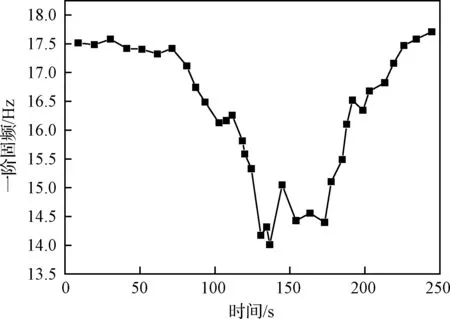
图24 气动力作用下一阶固频变化Fig.24 First order frequency variation under aerodynamic

4 考虑气动热作用的热力学及结构动力学分析

图25展示了各功能层的温度变化，尽管驻点温度最高达到1976 K，但TPS结构使热流传导减慢，最内部气密层的温度在有限时间内仅达到488 K，为驻点温度的1/4，从而满足了材料许用温度值。

图25 TPS各功能层温度变化Fig.25 Temperature variation of TPS functional layers

图26对比了气动热和气动力各自对结构应力的影响。热应力的变化存在两个峰值，分别由于结构热变形和内充压气体热膨胀占主导所致，如图中B点和C点所示，其应力幅值分别为33.5 MPa和31.1 MPa，分别发生在67 km 和45 km处。

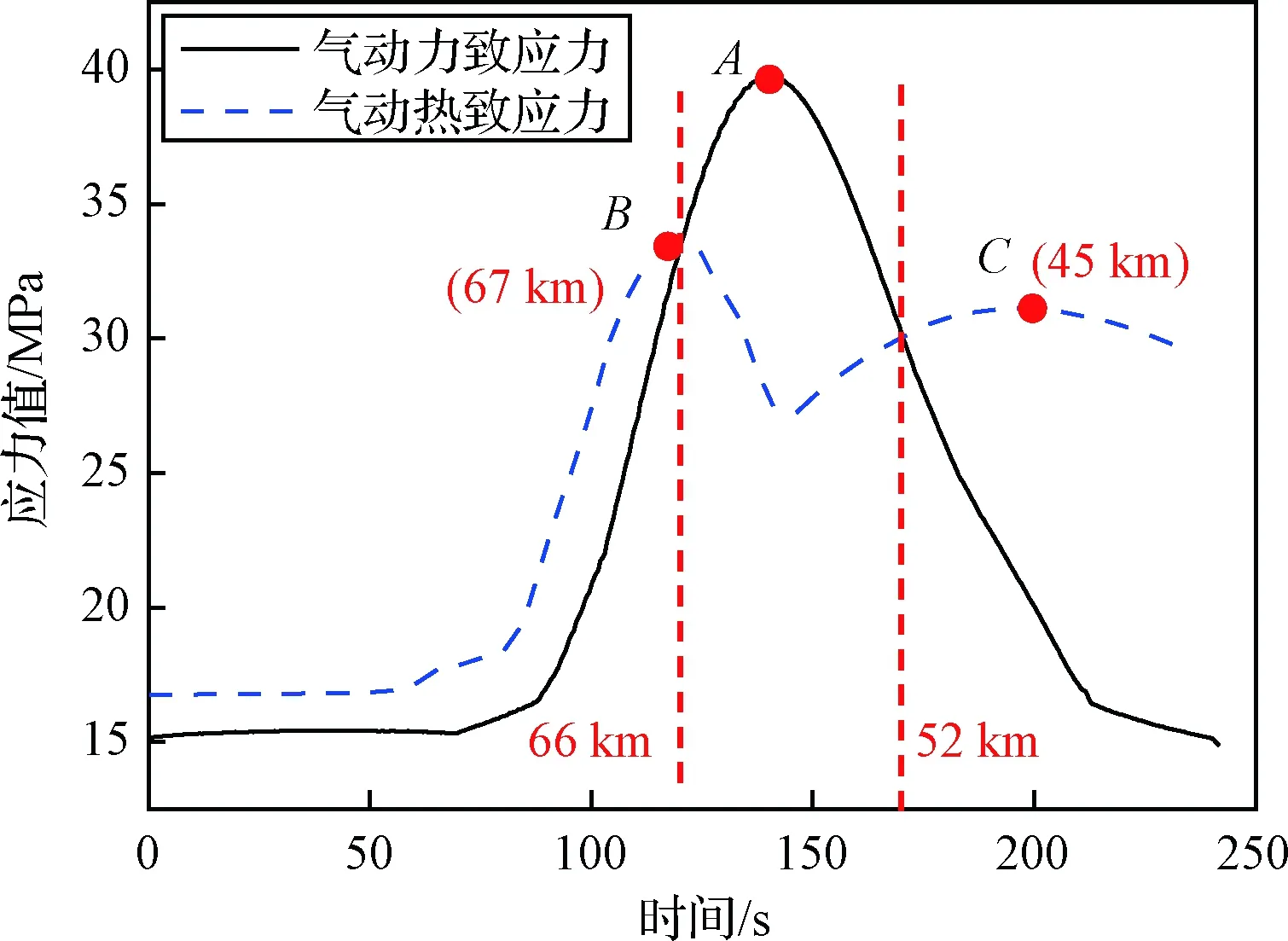
图26 气动热与气动力对结构应力的影响对比Fig.26 Comparison of aeroheating and aerodynamic on stress

图27着重选取B点和C点分析热变形和热膨胀对结构应力的影响规律。图27(a)中结构最大应力发生在后蒙皮上靠近内端位置，而蒙皮越靠外，应力下降越明显。图27(b)中应力分布和只考虑内充压时的应力相似，最大应力都位于最内层气囊与隔层连接处。

图27 结构热应力分布对比Fig.27 Comparison of thermal stress distribution

图28展示了B点和C点子午面变形图。图28(a)中最大变形位于最外层气囊处，为4.3 mm。将变形放大10倍后可知此时结构相对形状不发生变化，仅以内层为中心进行放大。图28(b)中最大变形发生在气囊处，大小为6.9 mm，而蒙皮上变形很小。

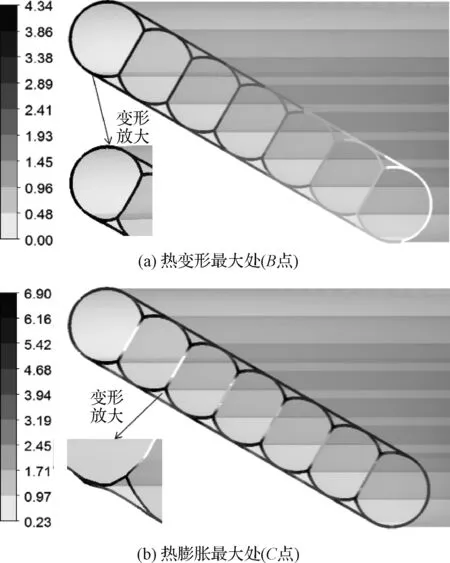
图28 结构子午面热变形Fig.28 Meridian thermal deformation of structure

图29对比了B状态和C状态各部分应力。图29(a)中蒙皮、气囊和隔层最大应力分别为33.5 MPa、25.5 MPa和23.3 MPa，且各部分靠近内层的应力增加明显，说明热变形对最内层结构的影响最大。图29(b)中蒙皮、气囊和隔层最大应力分别为8.2 MPa、21.4 MPa和31.1 MPa，隔层应力最为显著，而蒙皮应力很低。

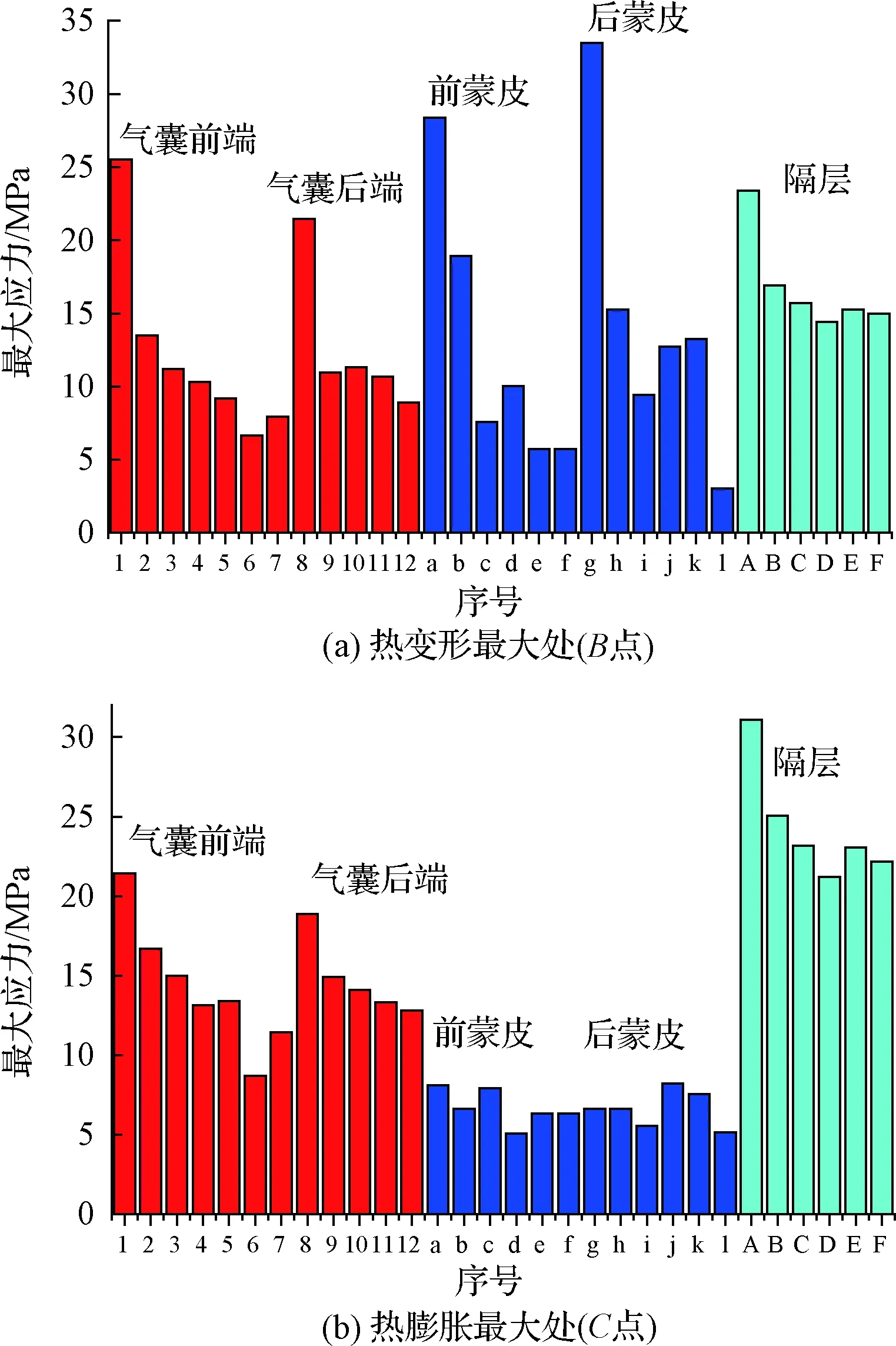
图29 结构各部分热应力幅值对比Fig.29 Comparison of thermal stress in different parts

图30展示了气动热作用下一阶固频的变化。其影响主要分为三部分：结构热变形、内充压气体热膨胀、材料弹性模量下降。在飞行前半段，温度升高带来的弹性模量下降占主导，固有频率从16.1 Hz下降至9.6 Hz；在飞行后半段，气体热膨胀占主导，使固有频率升高至24.8 Hz。

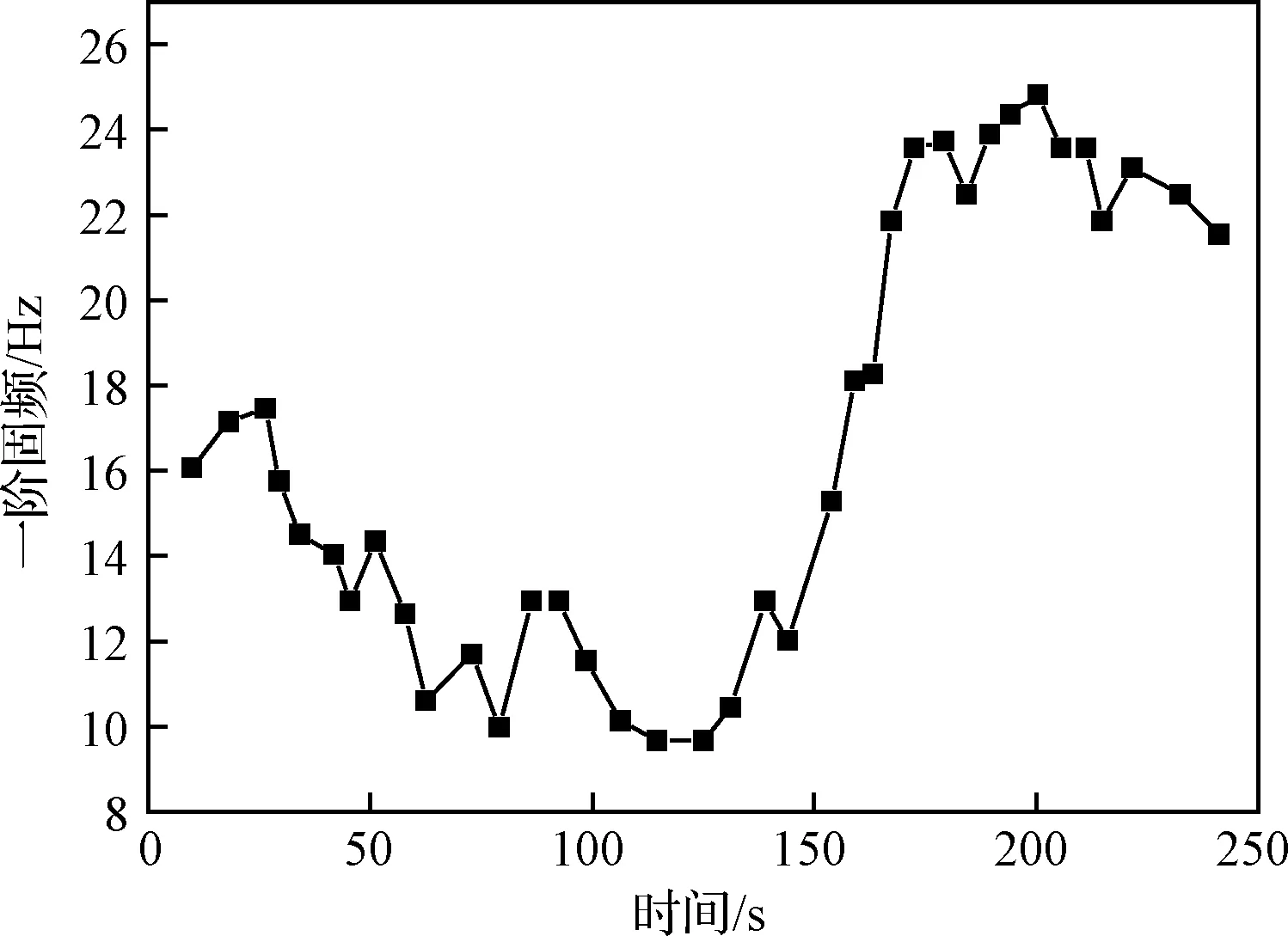
图30 气动热作用下一阶固频变化Fig.30 First order frequency variation under aeroheating

5 结构参数对飞行、流场及结构特性的影响

结构参数依次影响飞行动力学、空气动力学与结构动力学特性。本文先通过控制变量研究结构参数对各模块的单独影响，再利用流固耦合法研究各模块综合影响下的变化规律。

5.1 结构参数对各模块的单独影响

1)对飞行动力学的影响

通过表3可知，随着半锥角或气囊个数的增加，过载峰值有下降趋势。原因在于随着半锥角或气囊的增加，迎风面积增大导致阻力相应增加，速度衰减程度加大，过载峰值处的速度及气动载荷变小。

表3 结构参数对过载峰值的影响Table 3 Effect of structure on overload peak value

2)对空气动力学的影响

令来流条件相同，由表4可知,当半锥角从50°增大至65°时，驻点压力从4710 Pa增加至5234 Pa；平均压力增幅更大，共增加1410 Pa。其原因在于半锥角增大时，激波增压能力提高，强度增加，如图31所示。此外物面法向角的增大也使蒙皮上的平均压力有明显的升高。气囊个数增加时，由于前缘结构不发生变化，驻点压力和平均压力变化幅度很小。

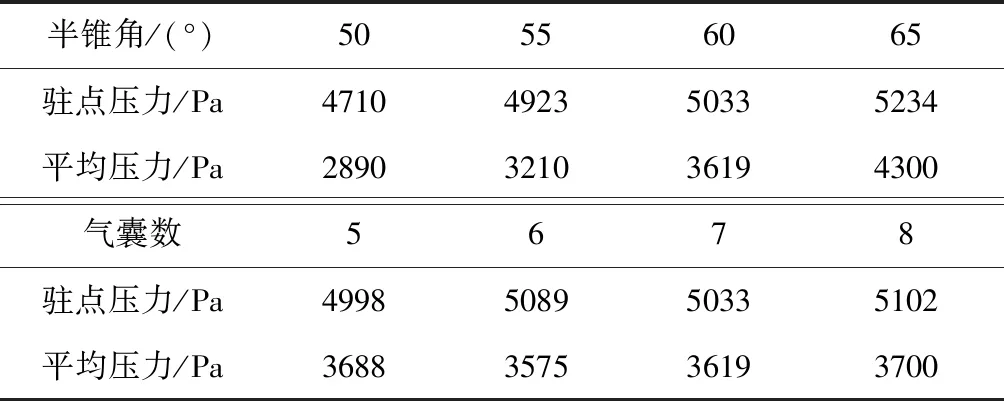
表4 结构参数对气动压力的影响Table 4 Effect of structure on aerodynamic pressure

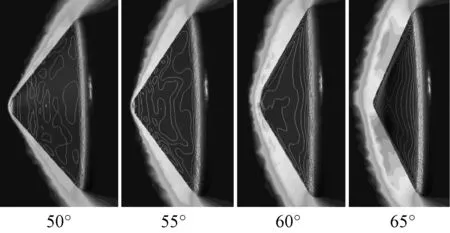
图31 不同半锥角流场压力对比Fig.31 Comparison of pressure at different half taper angles

3)对结构动力学的影响

令蒙皮上气动力与气动热相同，表5说明当半锥角增大时，两种应力均呈现上升趋势，但气动力的作用更为显著，使应力从16 MPa增加至60 MPa，这是由于半锥角变大，应力在纵轴上的分量减小，为了平衡外压，需要产生更大的应力。而增加气囊个数不改变前缘结构，对两种应力的影响较小。

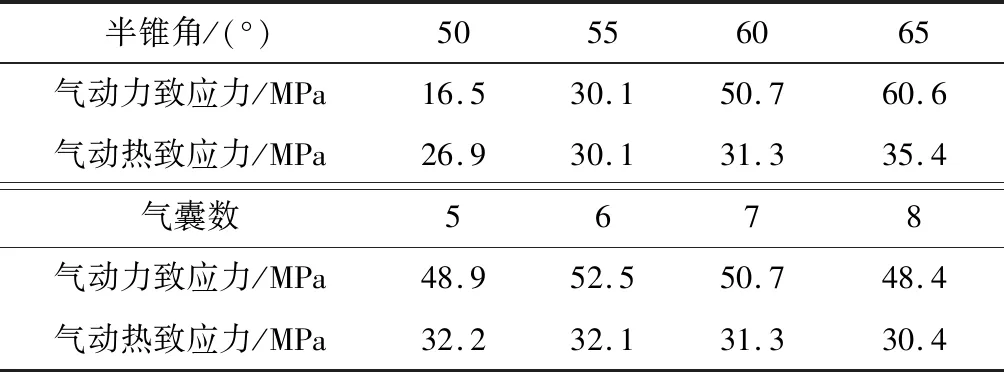
表5 结构参数对最大应力的影响Table 5 Effect of structure on maximal stress

5.2 结构参数对各模块的综合影响研究

综合上述各模块的影响，图32展示了不同结构对再入过程中两种应力的影响。两种应力的变化趋势相同，但气动力产生的应力变化更为明显：半锥角每增大5°，最大应力平均增加8.3 MPa，但在60°半锥角以上时变化有所减缓；气囊每增加一层，最大应力平均减小12.1 MPa。

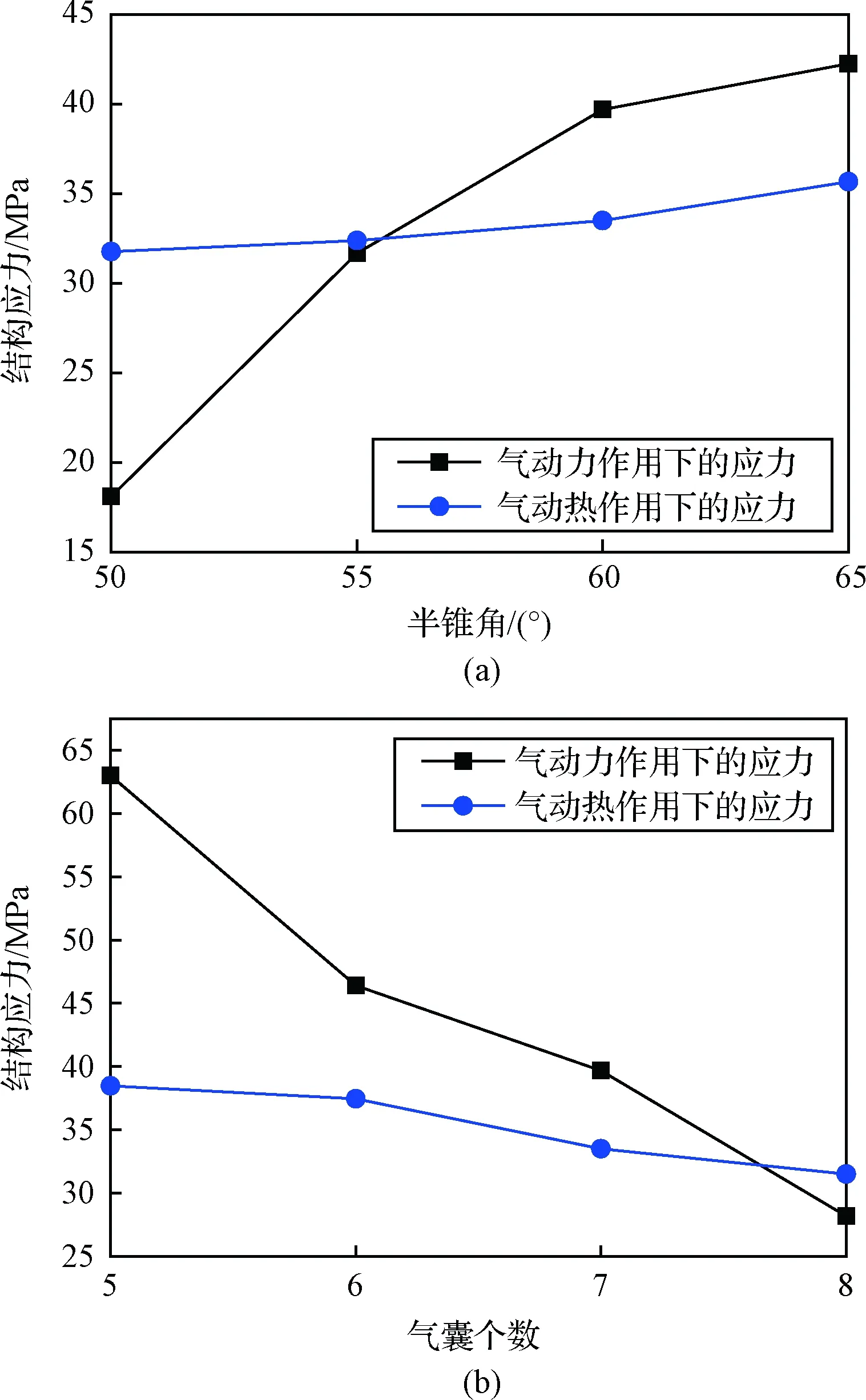
图32 再入过程下结构参数对最大应力的影响Fig.32 Effect of structure on maximal stress in reentry

综合之前的分析，半锥角增大时，激波强度与物面法向角增大导致的气动载荷上升占据主导，气囊个数增加时，由于其对流场和结构的影响改变较小，此时阻力增大带来的减速效果起主要决定作用。

6 结 论

1) 本文提出的基于飞行参数的CFD动态边界加载方法在模拟再入过程中的气动力时具有良好的能力。突破了现有研究中只通过对部分高度的计算结果进行插值来获得其余高度处气动力的思路，可以得到更为连续的气动力变化曲线。同时阻力系数的反馈修正进一步加强了飞行动力学计算的准确性。

2) 建立的流固耦合模型既考虑了结构变形对流场的影响，还涵盖了结构热传导与内充压气体热膨胀的作用，能有效模拟气动力与气动热对结构特性的影响。较已有方法而言该模型更全面地考虑了温度导致的内充压气体状态参数的改变。

3) 利用上述模型对典型轨迹下的结构特性进行了计算，并从气动力与气动热的角度分别进行了分析。发现气动力作用下结构最大应力从13.9 MPa升高至39.6 MPa，而由于其减弱了充压气体形成的刚度，使一阶固频下降3.4Hz。气动热作用下结构热变形和内充压气体热膨胀使应力曲线产生两处峰值，分别为33.5 MPa和31.1 MPa，而一阶固频受热膨胀的作用更明显，最大升高15.2 Hz。

4) 对不同结构尺寸下的结构特性进行了对比研究，发现气动力与气动热作用下的结构应力变化趋势相同，但气动力作用下其应力变化更明显：半锥角每增加5°，气动力作用下的最大应力平均增加8.3 MPa，此时激波强度与物面法向角增大导致的气动载荷上升占据主导；气囊数目每增加1层，气动力作用下的最大应力平均减小12.1 MPa，此时阻力增大带来的减速效果起主要决定作用。