航天器末端拦截自适应博弈策略
2020-04-15王淳宝孙兆伟孙楚琦
王淳宝,叶 东,孙兆伟,孙楚琦
(哈尔滨工业大学航天学院,哈尔滨 150001)
0 引 言
卫星作为空间力量重要组成部分,具有传送信息量大、不受地形限制等优点,可以为指挥者制定策略提供战场信息,也可为导弹等作战单元提供导航制导信息[1]。因此为了夺取战时空间信息主动权,对敌方卫星实施拦截打击有着重要意义。
针对拦截问题,文献[2-3]基于滑模面进行了导弹的制导与控制一体化设计,仿真表明了采用所设计的控制方法能够满足拦截要求。赖超等[4]考虑目标进行机动时的拦截策略,基于动态面和扩张状态观测器对制导与控制进行了设计,仿真分析了目标在进行正弦机动时,采用相应的控制策略能够实现对目标的精确拦截。虽然上述文献对目标拦截问题均进行了研究,但其中的目标并未进行机动或未采取最优的机动策略。而随着科技的发展,目标获取空间战场信息能力的提高,可以对战场情报进行分析,并做出相应的决策,采取最优躲避策略以应对不同的战场态势,此时拦截策略的设计需要考虑目标机动的最优性,传统的拦截方法已不能满足拦截要求,单边拦截策略已不再适用。此外,随着卫星任务的复杂化及多样化,目标的被动逃逸可能会影响其任务的实施,此时为了避免具有重要价值的卫星被拦截,附近通常会存在伴飞星进行主动防御,这种态势无疑增加了拦截难度,对空间拦截提出了更高的要求,因此研究存在防御器的多边拦截策略有着重要的意义。
针对多边拦截问题,学者们已经进行了充分的研究。史明明[1]分别考虑了卫星远程拦截、近程拦截时的控制策略,远程拦截时建立了考虑J2摄动的动力学模型,近程拦截以CW方程为模型,基于微分对策分别给出了相应的最优控制策略。Horie等[5]基于飞机三维动力学模型,通过微分对策理论将拦截问题转化为两点边值问题,通过仿真分析,最优飞行轨迹分为偏离垂直平面以及垂直面内运动的两个阶段。Shinar等[6]考虑二维平面拦截,且离散控制的情况,设计了拦截器在有限步数内成功拦截目标的最优控制策略。当拦截器动力学模型较复杂时,通过微分对策理论会得到非线性强耦合的两点边值问题方程组,一般难以求解。文献[7-8]给出了一种求解两点边值问题的方法,即半直接配点法:将整个控制过程离散化,分别对每段进行优化设计,以得到完整的控制规律,该方法可以有效地求解两点边值问题。
当拦截器距离目标较近时,拦截过程进入末端拦截,此时拦截器利用自身的敏感器可以获得精度较高的目标信息,从而实现精确拦截。针对末端拦截问题,Prussing等[9-10]应用主矢量理论分别研究了多脉冲逃逸策略以及拦截策略。文献[11]考虑航天器拦截目标后返回原轨道的情况,通过在目标函数中引入一个参数k对路径进行约束。Stupik等[12]基于CW方程,应用最大值原理求解拦截控制问题,对于开环解应用粒子群优化方法进行求解,闭环解应用Kriging方法求解,其中的Kriging方法是插值和外推相结合的方法,是一种状态反馈控制器。Gutman等[13]在双积分动力学模型的基础上,以终端相对距离为指标建立了拦截器与目标的控制策略,并分别给出了在极坐标、球坐标下的策略形式。文献[14-15]在给出拦截器与目标的控制策略的基础上,建立了关于拦截剩余时间的一元四次方程,以求解终端拦截时间,并讨论了方程的分叉现象。文献[16]讨论了拦截过程中角度测量存在噪声的情况,通过状态观测器实现对角度的估计,再将其应用于控制策略。
对于三星博弈问题,Garcia等[17-18],Pachter等[19-20]假设拦截器、防御器与目标三者的速度大小不变,因此三者运动轨迹为直线,应用微分对策求解最优飞行路径角,经过进一步分析,三者轨迹覆盖区域为阿波罗尼圆,简化了求解过程。文献[21]以简单的双积分系统为模型,研究了拦截器、目标和防御器三者的追逃控制策略,同样对终端拦截时间进行了求解,仿真表明了过短的拦截时间不能实现对目标的拦截。
虽然对于航天器末端拦截问题已经存在较多的研究,但大多局限于拦截器与目标的双星博弈。对于三星博弈问题,大多局限于针对简化模型进行研究,与实际情况偏差较大。此外,对于不同博弈态势,终端拦截时间作为博弈策略参数,其设定具有随机性,导致策略自适应性较差。本文针对具有防御器的三星博弈末端拦截问题进行研究,由于各航天器之间利益对立,符合博弈思想,因此采用微分对策理论进行求解,推导了各航天器的博弈策略,并提出了时间分析方程以计算终端拦截时间,提高策略的自适应性。
本文安排如下:首先建立了航天器末端拦截动力学模型。其次,讨论了双星博弈态势,基于零控脱靶量推导了拦截器与目标的最优博弈策略,同时建立双边时间分析方程以消除终端拦截时间的随机特性,将随机终端博弈转化为固定终端博弈。再次,将双星博弈扩展为目标携带防御器的三星博弈,类似的方法推导了各航天器的分段博弈策略,同时修正双边时间分析方程以适应三星博弈态势。最后,将建立的博弈策略、时间分析方程应用于三星博弈拦截,并进行了相应的仿真分析。
1 末端拦截动力学模型
在末端拦截过程中,拦截器与目标的相对距离较近,因此在拦截器附近建立参考卫星,如图1,其中,O1为参考卫星,P为拦截器。设参考卫星运行在圆轨道,以参考卫星为原点,O1x轴沿着参考卫星地心矢径方向,O1z轴沿着轨道角动量方向,O1y轴满足右手定则,定义轨道坐标系O1xyz,在该坐标系下,拦截器相对参考卫星的动力学方程可以简化为CW方程。
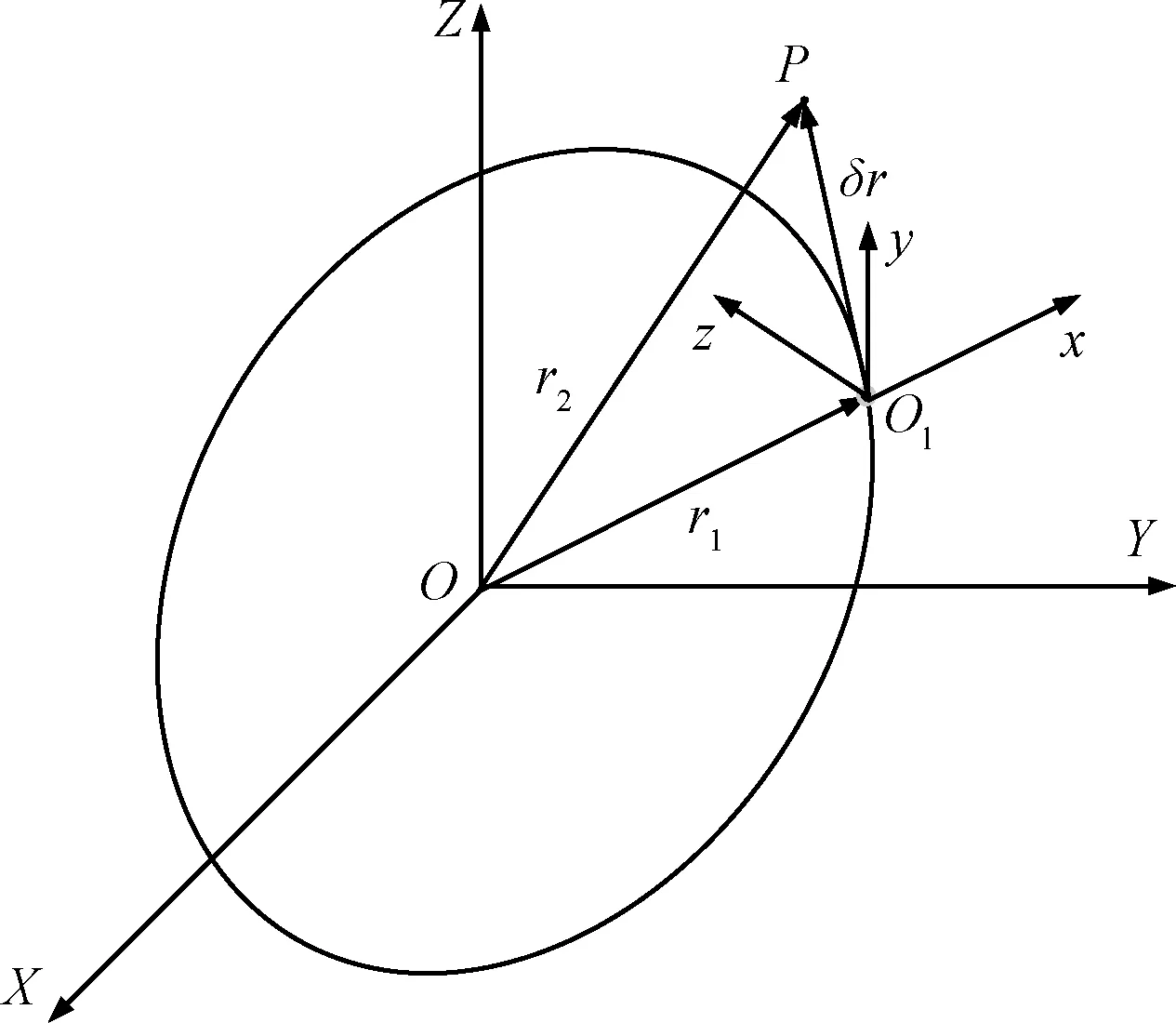
图1 拦截器与参考卫星Fig.1 Interceptor and reference satellite
(1)
式中:x,y,z为拦截器相对参考卫星的位置,ω为参考卫星的轨道角速度,ux,uy,uz分别为拦截器的控制输入。
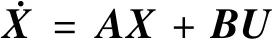
(2)
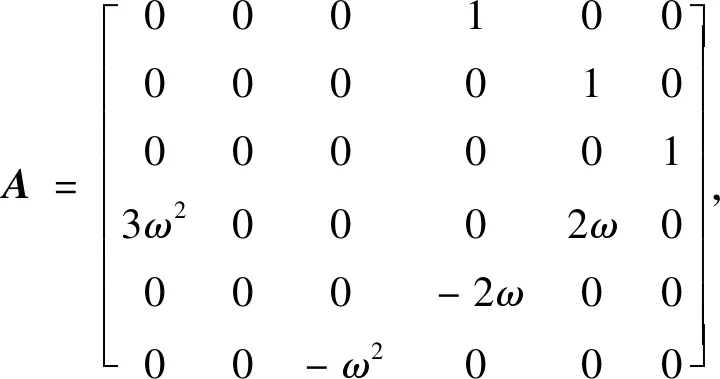
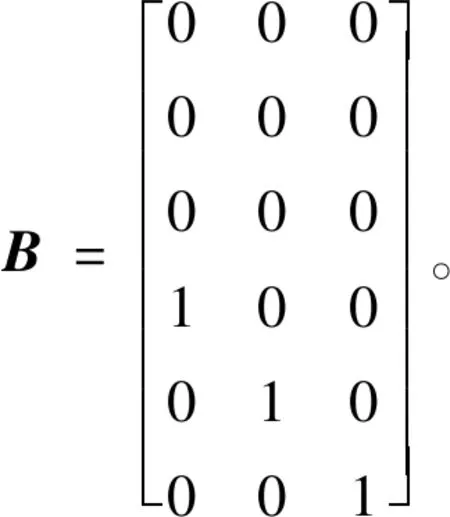
由线性系统理论可得状态转移矩阵为
(3)
其中的子矩阵分别为[22]
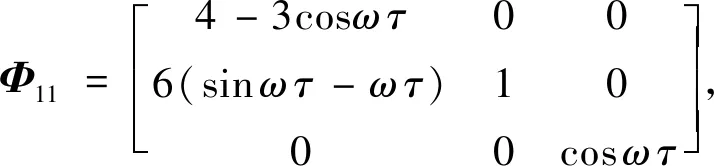
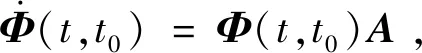
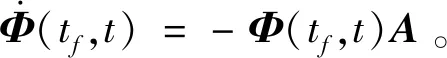
2 双星博弈拦截策略
若目标不携带防御器,则拦截过程呈现双星博弈态势,此时拦截器与目标的动力学方程均满足CW方程,即
(4)
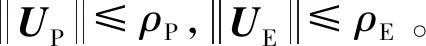
定义拦截器与目标的相对状态
XPE=XP-XE
关于时间求导,并结合式(4)整理可得相对动力学方程
(5)
式中:C=B。
2.1 最优博弈策略设计
在拦截过程中,拦截器与目标围绕拦截终端距离展开争夺,因此只需考虑两星的位置矢量[14],定义零控脱靶量ZPE(t)对系统进行降维处理
ZPE(t)=MΦ(tf,t)XPE
(6)
式中:M=[I3,03×3],I3为3×3的单位阵。
对式(6)求导,并综合式(5)可得
M(ΦBUP-ΦCUE)=BPUP+CEUE
(7)
式中:tf为终端拦截时间,且BP=MΦ(tf,t)B=Φ12,CE=-MΦ(tf,t)C=-Φ12。
(8)
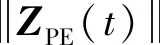
(9)
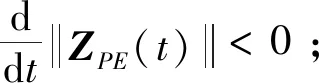
(10)
(11)
2.2 终端拦截时间的确定
由式(10)~(11)以及零控脱靶量定义式(6)可知,终端拦截时间是调整博弈策略的重要参数。选取不同终端拦截时间tf,将拦截器与目标的策略(10)~(11)代入式并积分,可得在不同拦截时间条件下,拦截器与目标相对距离的变化,如图2所示。可以看出,当选取特定的拦截时间后,拦截器会在该时刻实现对目标的拦截,并不会提前拦截目标,因此,终端拦截时间的设定直接影响了博弈结果。
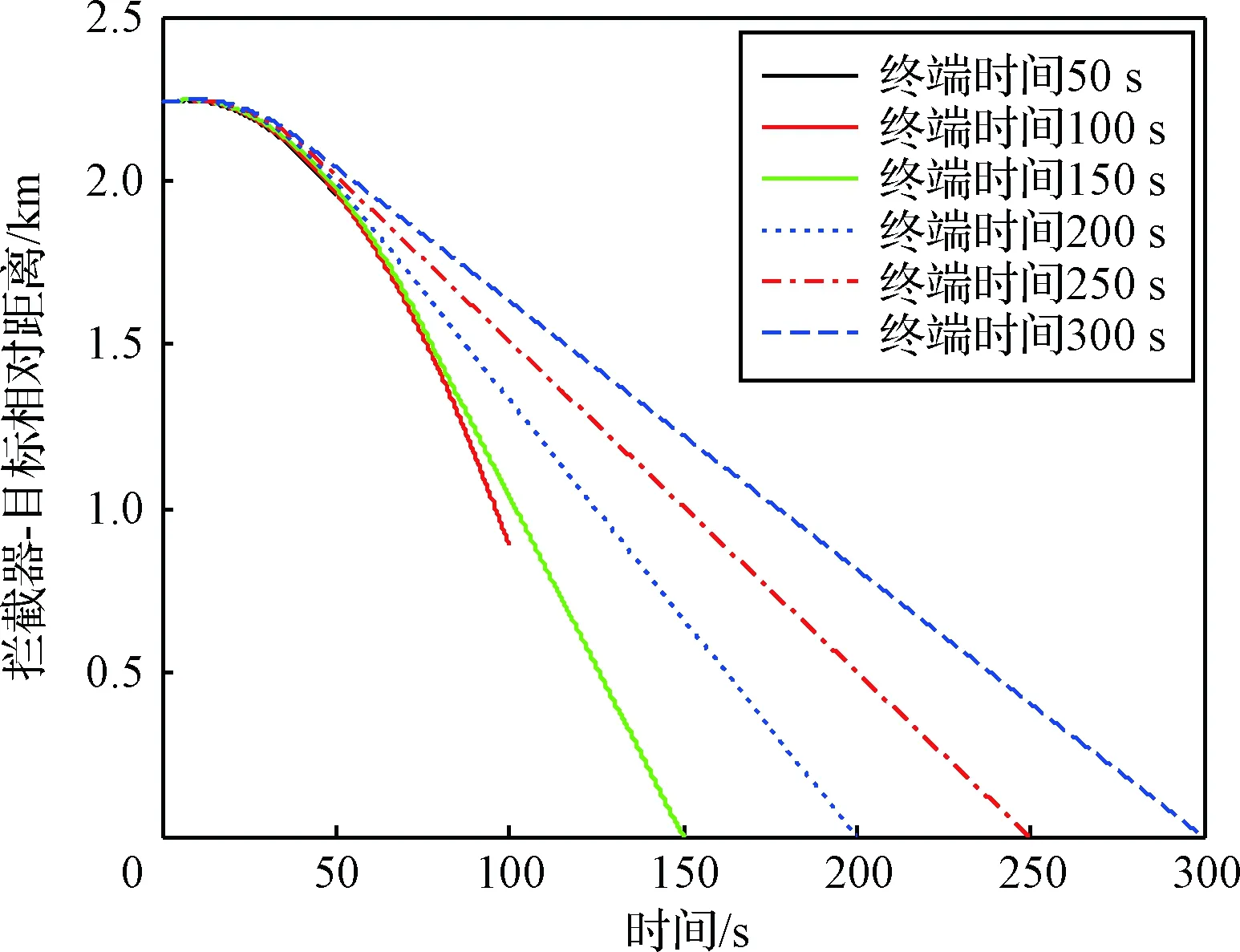
图2 不同拦截时间下拦截器与目标相对距离的变化Fig.2 Relative distance between interceptor and target with different intercept time
但在文献[1]和[23]中,终端拦截时间均直接给定,随机性较大,对于不同博弈态势,需要设定不同的拦截时间,自适应性较差。针对该问题,提出双边时间分析方程以确定终端拦截时间,达到消除拦截时间随机性,提高策略自适应性的目的。
将拦截器与目标的博弈策略(10)~(11)带入式(7)中得
(12)
定义拦截剩余时间tgo=tf-t,当终端拦截时间不变时,有dtgo=-dt,于是
(13)
积分式(13)得到零控脱靶量ZPE(tgo)随剩余时间tgo的变化关系
(14)
定义ZPE(0)=l,其中l为拦截器的拦截半径,对式(14)取范数并记为
(15)
此外,对于式(6)有
(16)
联立式(15)~(16)两式,可以得到关于剩余时间tgo的方程,即
(17)
3 三星博弈拦截策略
对于具有重要价值的目标,附近通常存在伴飞防御器,以保护其不被拦截[24-25],此时末端拦截会呈现三星博弈态势,博弈过程更加复杂,拦截更加困难。针对该问题,需要重新设计航天器博弈策略,并对双边时间分析方程进行修正。
在三星博弈态势下,拦截器、目标、防御器三星的运动均满足CW方程,即
(18)
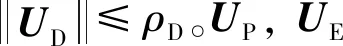
定义拦截器与目标的相对状态XPE,以及拦截器与防御器的相对状态XDP,对其求导,并结合式(18)整理得到相对状态方程
(19)
(20)
式中:D=B。
3.1 分段最优博弈策略设计
与第2节类似,分别定义ZPE(t),ZDP(t)为拦截器与目标、防御器与拦截器的零控脱靶量
ZPE(t)=MΦ(tf1,t)XPE
(21)
ZDP(t)=MΦ(tf2,t)XDP
(22)
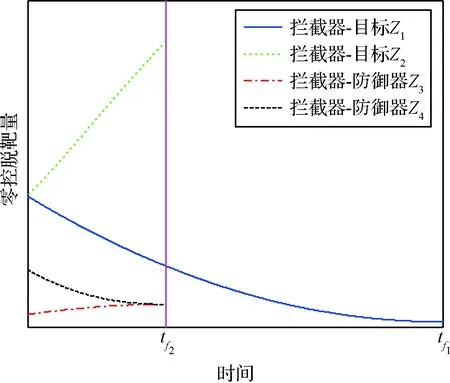
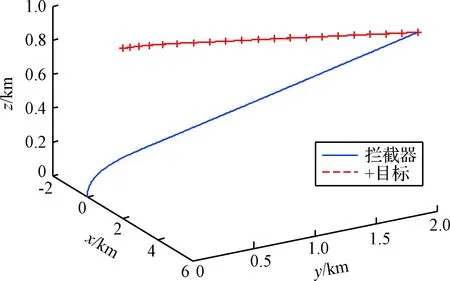
式中:tf2,tf1分别为防御器反拦截时间和终端拦截时间,且满足tf2 对式(21)~(22)两式求导,并结合式(19)~(20)两式整理得 (23) BP2UP+DDUD (24) 式中:BP1=DD=MΦ(tf1,t)B=Φ12(tf1,t),BP2=CE=-MΦ(tf2,t)B=-Φ12(tf2,t)。 在三星博弈拦截对抗中,拦截器与目标利益对立,拦截器与防御器同样存在利益对立关系,导致三星之间相互影响。为了降低该影响,以tf2作为博弈策略切换时间将其化为分段双星博弈:第一阶段为拦截器与防御器的双星博弈,此阶段拦截器只躲避防御器;第二阶段为拦截器与目标的双星博弈,此阶段拦截器已成功躲避防御器,只考虑拦截目标。因此定义指标函数JPE,JDP分别为tf1,tf2时刻的相对零控脱靶量 (25) (26) (27) 对式(25)进行类似地推导并综合上述分析,可得各航天器的分段最优博弈策略为 当t0 (28) (29) 当tf2 (30) UD=0 (31) 目标的博弈策略一直为 (32) 当拦截器采用策略(30)时,拦截器与目标之间的零控脱靶量变化如图3中的Z1,拦截器与防御器之间的零控脱靶量变化如图3中的Z4;当拦截器采用策略(28)时,拦截器与目标之间的零控脱靶量变化如图3中的Z2,拦截器与防御器之间的零控脱靶量变化如图3中的Z3。 图3 不同策略下零控脱靶量的变化Fig.3 Changes of zero effort miss under different strategies 可以看出,当拦截器躲避防御器时,会导致拦截器与目标之间的相对距离变大,因此为了达到拦截目标的快速性,需要提前拦截器博弈策略的切换时间点,在t0~tf2之间定义躲避时间tf3,拦截器在t0~tf2时间内采取如下分段策略: 防御器与目标的策略不变,记此时三星的博弈策略为(*)。相应的拦截过程为:当t0 由于策略(30)会导致拦截器与防御器之间的相对距离减小,因此需要合理设定切换时间点tf3,以保证在t0~tf2范围内拦截器不被防御器反拦截。 定义拦截器与防御器的安全距离m,在t0~tf2时间内各航天器采取相应的分段博弈策略(*),带入式(24),同时令tgo2=tf2-t,由终端拦截时间tf2不变得到dtgo2=-dt,因此 当t0 (33) 当tf3 (34) 积分式(33)~(34),并分别记为 ZDP(tgo2)=g1(tgo2) (35) (36) 由拦截器不被反拦截得到tf2时刻的终端条件 (37) 同时,在tf3时刻有状态连续条件 g1(tf2-tf3)=g2(tf2-tf3) (38) 综合式(35)~(38)以及零控脱靶量的定义式(22)可解出最短躲避时间tf3。 为了验证博弈策略及时间分析方程的有效性,分别对双星博弈随机、固定终端拦截,以及三星博弈随机、固定终端拦截四种态势进行仿真验证。 初始条件如下:设拦截器、目标、防御器均在地球同步轨道附近运动,则将参考卫星选为GEO轨道上与其相近的卫星,轨道角速度为w=7.2722×10-5rad/s。拦截器的推力幅值为ρP=0.686 m/s2,目标的推力幅值为ρE=1/2ρPm/s2,防御器的推力幅值为ρD=5/8ρPm/s2。拦截器初始状态为[0, 0, 0, -0.005, 0, 0.005],目标初始状态为[2, 0, 1, 0, 0.005, 0],防御器初始状态为[1, 0, 0, 0.005, 0, 0],位置单位为km,速度单位为km/s。设拦截器与目标之间的拦截距离为1 m,拦截器与防御器之间的安全距离为100 m。假设防御器反拦截时间tf2=200 s。 1) 双星博弈随机终端拦截,此时拦截空间只存在拦截器与目标。设终端拦截时间为200 s,图4和图5分别给出了该博弈态势下,拦截器与目标的运动轨迹和相对距离的变化。可以看出,在终端拦截时间为200 s的情况下,拦截器可以实现对目标的拦截,但由图2可知,设定拦截时间为200 s不是最快的拦截方案,即可以在更短的时间内拦截目标。 图4 随机终端下的双星博弈运动轨迹Fig.4 Motion trajectory of two-satellite game with stochastic terminal time 图5 随机终端下的双星博弈相对距离Fig.5 Relative distance of two-satellite game with stochastic terminal time 图6给出了拦截器与目标的三维运动轨迹,图7绘制了两星相对距离的变化情况,可以看出,在126.28 s时,两星的相对距离为0.7 m,满足拦截条件。 图6 固定终端下的双星博弈运动轨迹Fig.6 Motion trajectory of two-satellite game with fixed terminal time 图7 固定终端下的双星博弈相对距离Fig.7 Relative distance of two-satellite game with fixed terminal time 3) 三星博弈随机终端拦截,即博弈空间存在拦截器、目标与防御器。此时的拦截时间、躲避时间均是随机变量,需要人为设定。 图8绘制了在不同躲避时间下,拦截器与目标终端距离随拦截时间的变化情况,此时暂不考虑拦截器是否被防御器反拦截。可以看出,随着躲避时间的增加,拦截目标所需时间也相应地增加,因此在博弈过程中,为了快速拦截目标,躲避时间不应过长。 图9绘制了在不同拦截时间下,拦截器与防御器最短距离随躲避时间的变化情况,类似地,此时暂不考虑是否成功拦截目标。可以看出,拦截器与防御器最短距离与躲避时间之间呈现非线性关系,而且终端拦截时间对躲避时间也会产生影响,当设定拦截时间大于300 s时,拦截器不被反拦截至少需要15 s,但当拦截时间设定为200 s时,相应的躲避时间只需6 s左右,因此在博弈开始前,终端拦截时间与躲避时间应合理地进行设定,以达到最优拦截状态。 图8 拦截器与目标终端距离Fig.8 Terminal distance between interceptor and target 图9 拦截器与防御器的最短距离Fig.9 Minimal distance between interceptor and defender 若不采用时间方程计算拦截时间与躲避时间,为了保证成功拦截目标且不被反拦截,拦截器通常会选取较大的拦截时间,相应的躲避时间也会较大。这里选取拦截时间tf1=500 s,躲避时间tf3=50 s进行仿真,此时拦截器、目标和防御器的三维运动轨迹如图10,图11给出了三星之间的相对距离随时间的变化规律。 从图11中可以看出,博弈过程中拦截器与目标之间的相对距离峰值较大,虽然最后成功拦截,但消耗了较多的时间,拦截效率较低。同时拦截器与防御器之间的最短相对距离为140 m,有被反拦截的风险。由图8,图9可知,相比于选取较大的拦截时间与躲避时间,存在着更优的时间选取方案。 图10 随机终端下的三星博弈运动轨迹Fig.10 Motion trajectory of three-satellite game with stochostic terminal time 4) 三星博弈固定终端拦截。此时通过时间分析方程得到终端拦截时间tf1=200 s,躲避时间tf3=8 s。相比于2)的双星博弈固定终端拦截,终端拦截时间明显增加,防御器的引入直接减慢了博弈速度。相比于3)的三星随机终端博弈,时间方程可以计算得到图8,图9中最佳的时间选取方案,此时的拦截方案更优。 图12、图13分别给出了三星的运动轨迹以及相对距离的变化情况。可以看出,拦截器与目标的终端距离为1 m,满足拦截条件。此时拦截器与防御器之间的最小相对距离为190 m。与3)的三星随机终端博弈相比,8 s的躲避时间就可以保证拦截器不被防御器反拦截,明显缩短了躲避时间,节约了拦截成本,提高了拦截效率。 图12 固定终端下的三星博弈运动轨迹Fig.12 Motion trajectory of three-satellite game with fixed terminal time 图13 固定终端下的三星博弈相对距离Fig.13 Relative distance of three-satellite game with fixed terminal time 本文研究了航天器末端拦截博弈问题,基于微分对策理论建立了多边拦截策略,具有以下特点: 1) 针对策略中终端拦截时间的设定随机性问题,创新性地提出了时间分析方程,将随机终端博弈转化为固定终端博弈,提高了拦截策略的自适应性。 2) 拦截空间中防御器的引入导致三星博弈态势,以及拦截时间的延长,通过博弈策略的切换将其化为分段双星博弈,降低了拦截难度。 3) 针对不同博弈态势进行仿真,结果表明应用所建立的博弈策略,拦截器在不被防御器反拦截的情况下,能够实现对目标的打击,具有一定的工程价值。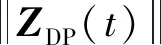
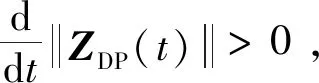
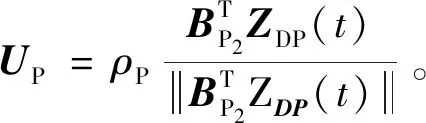
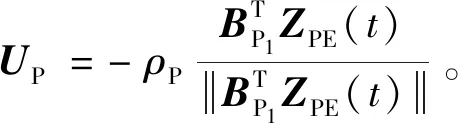
3.2 终端拦截时间的分段确定
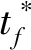
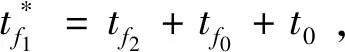
4 仿真校验
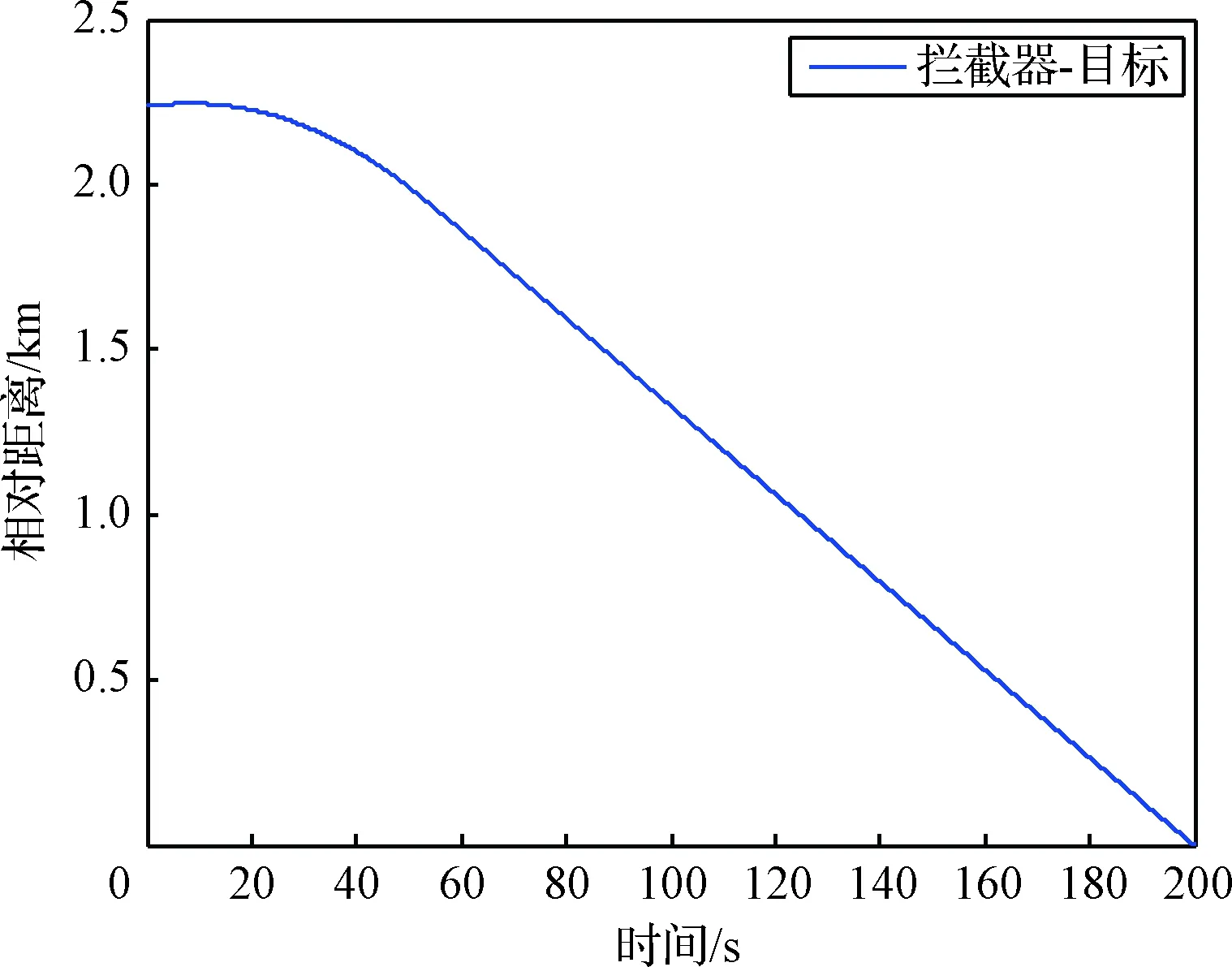
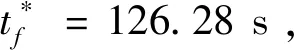
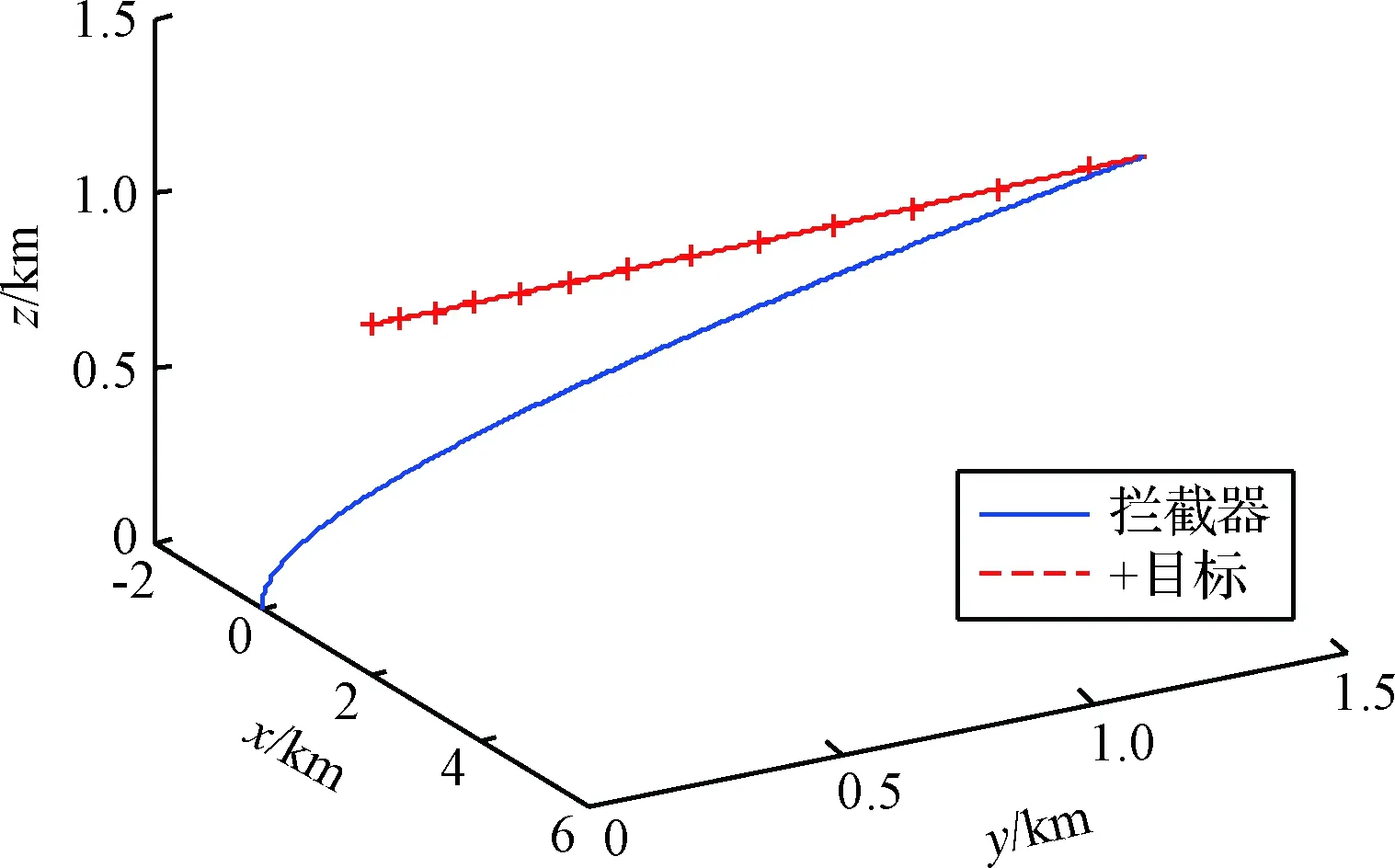
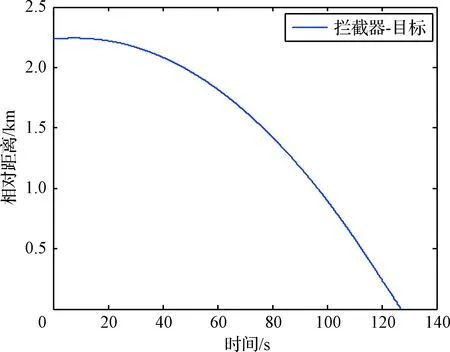


5 结 论
