一种小型固体运载火箭末级多约束制导方法
2020-04-15李新国黄建友
张 迁,许 志,李新国,高 峰,黄建友
(1. 西北工业大学航天学院,西安 710072;2. 陕西省空天飞行器设计技术重点实验室,西安 710072;3. 中国运载火箭技术研究院,北京 100076)
0 引 言
随着“快速发射”要求的不断提高,小型全固体运载火箭凭借可快速机动发射、可靠性高、成本低等优势而备受关注[1]。为了提高质量比及可靠性,取消了推力终止机构的固体运载火箭,只能耗尽关机而不能进行制导关机,使其制导算法必须考虑耗尽关机速度管控问题[2],而不再是燃料最省的两点边值问题[3-5]。此外,由于固体发动机具有工作时间短、推力大等特点,运载火箭必须采用“助推-滑行-助推”的飞行模式才能将有效载荷送入运行轨道,确定滑行点火时间是制导的核心算法[6-7]之一。由于固体火箭发动机性能受环境影响较大而导致关机时间无法准确预估,要求制导算法必须具有较强的偏差适应能力才能保证入轨精度[8]。综上所述,这给小型全固体运载火箭带来了更高的制导技术需求。
固体火箭的制导算法研究主要集中在基于改进闭路制导,并结合能量管理算法[9-10]实现了终端入轨任务要求。但该算法忽略了制导过程中位置矢量的变化对终端约束产生的影响,导致终端入轨精度及鲁棒性较差。针对固定总冲约束的两点边值问题,本研究团队基于轨道动量矩的变化推导出定点制导算法[11-12],并以此为基底制导算法求解点火时间及制导指令。在多子级飞行条件下对于耗尽关机速度管控问题,文献[11]通过轨道能量匹配的方式提前将运载火箭动能与势能进行分配;文献[12]采用定点制导结合速度管控模型设计的思想,在中间过渡级将速度管控产生的附加位置量分解到轨道高度上。尽管上述方法均实现了在耗尽关机方式下的入轨任务,但是由于避开了末级多约束制导问题导致入轨精度、鲁棒性及适应性降低。
因此,针对耗尽关机末级多约束制导问题,本文重点研究了定点制导算法对速度管控的适用性及速度管控过程引起的耦合项抑制问题。在前期研究文献[11-12]的基础上分析了速度管控与终端约束之间的耦合关系,并在定点制导算法的基础上推导出适用于速度管控的拓展理论算法,建立了需要速度与速度管控方向之间的理论关系,得到了滑行时间、制导矢量及速度管控方向的解析表达式,并通过仿真验证了所提制导方法的制导精度和鲁棒性。
1 固体火箭多约束制导问题
小卫星等空间载荷通常以太阳同步轨道(SSO)为目标,为进入较高的太阳同步轨道,固体运载火箭需要采用四级串联的方案并采取“助推-滑行-助推”制导模式。其飞行模式一般可以分为一级助推段、二级助推段、三级滑行段、三级助推段、四级滑行段、四级助推段。火箭第一、二级发动机推力大可快速进入真空环境,该飞行阶段基本位于大气层内,后四个飞行阶段处于真空环境下,其飞行任务剖面如图1所示。
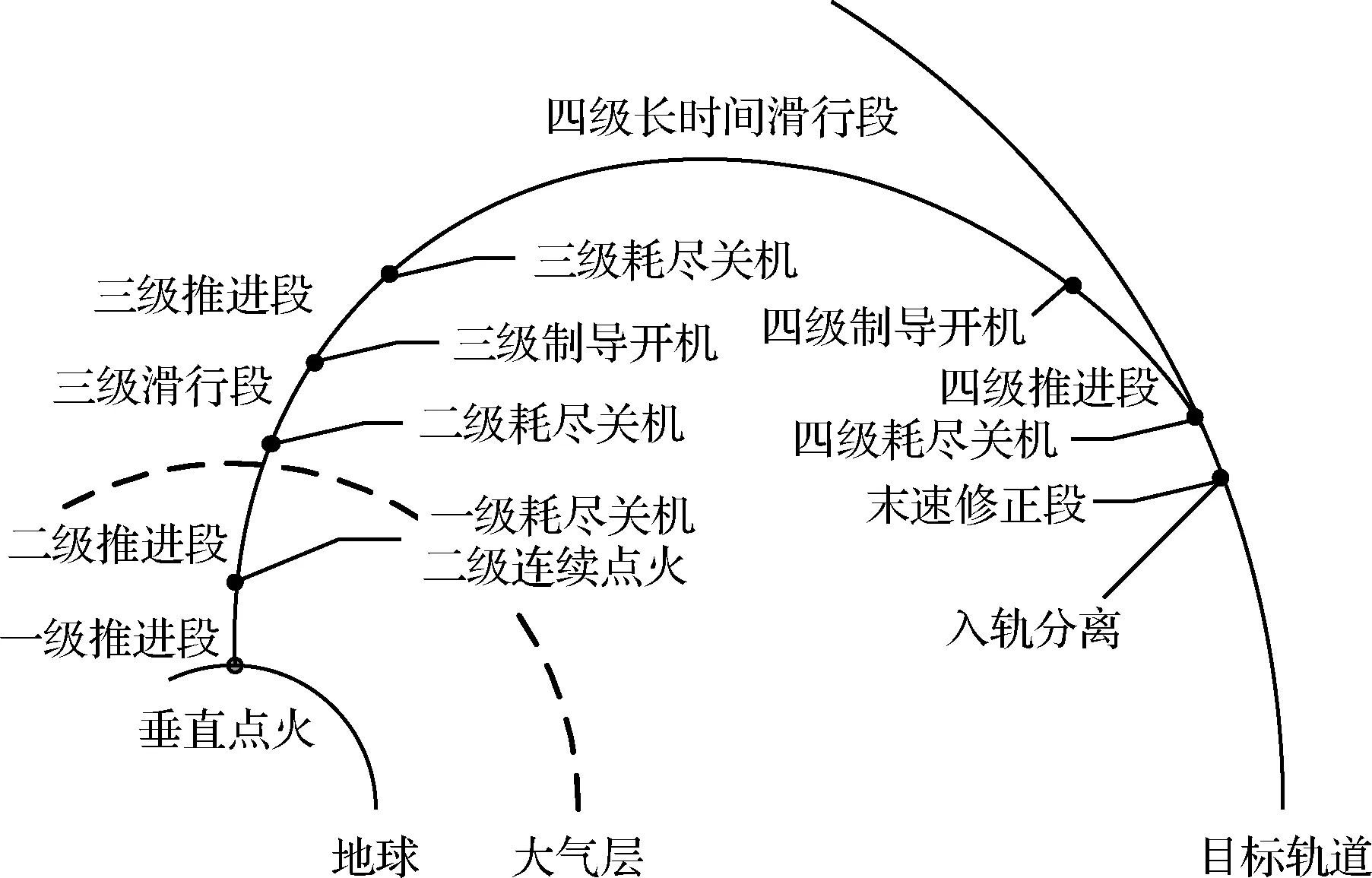
图1 典型固体运载火箭飞行时序剖面Fig.1 Typical launch process of a four-stage rocket
1.1 质心运动模型
在发射惯性坐标系下运载火箭质心运动方程[11]表示为:
(1)
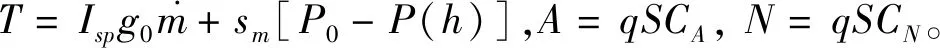
(2)
对于大气层外的“助推-滑行-助推”飞行模式,运载火箭运动方程式(2)中的推力为:
(3)
式中:tig为火箭发动机点火时刻。固体运载火箭发动机的推力大小与秒流量不可调节,式(1)里实际上需要确定出箭体方向xb的控制指令,使运载火箭以耗尽关机的方式满足入轨约束条件。
1.2 多约束制导问题
运载火箭处于无动力的滑行轨道时,根据开普勒轨道性质:
(4)
而在火箭发动机点火工作后,根据式(2)和式(4)可得运载火箭关机点的状态矢量表达式:
(5)
式中:μ为地球引力常数,r0,v0表示火箭当前位置矢量和速度矢量,rig,vig表示点火时刻位置矢量和速度矢量,rf,vf表示终端位置矢量和速度矢量。对于空间载荷的飞行轨道,通常约束轨道根数中的半长轴aorb.f、偏心率eorb.f及轨道倾角iorb.f等,其表达式如下:
(6)
此外,对于耗尽关机的固体火箭发动机,所能够提供总的视速度模量WM和视位置模量RM表达式为:
(7)
耗尽关机的固体运载火箭由于失去了制导关机的物理条件,导致对终端速度管控能力薄弱。因此,为了满足飞行任务的适应性要求,进行速度管控是解决终端多约束问题的主要途径。
1.3 耗尽关机速度管控问题
在耗尽关机方式下,由于发动机产生的总视速度模量一定,需要通过速度管控算法[13-15]产生附加姿态来消耗多余能量,使速度增量在固定弧长约束下的矢量弦长满足制导要求,速度管控算法的制导原理如图2所示。
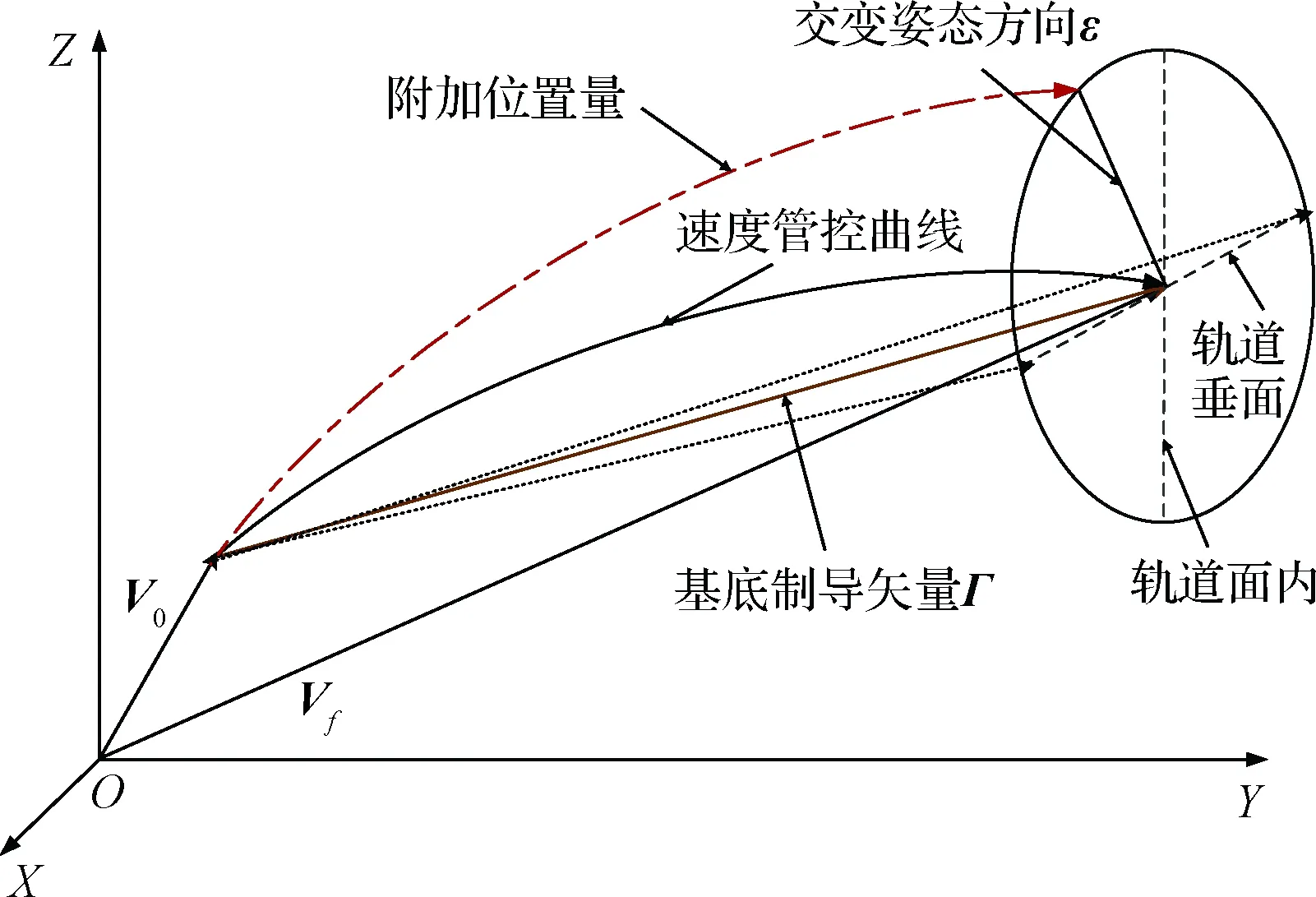
图2 基底制导算法耦合速度管控算法的制导剖面Fig.2 Profile of the proposed guidance under pointing algorithm with energy management method
耗尽关机制导问题的本质是求解固定弧长约束下的两点边值问题,本文将此问题分解为多约束制导问题和交变姿态速度管控问题,从而使复杂问题简化。多约束基底制导算法计算所需的速度矢量Γ,速度管控算法主要解算视速度模量WM固定条件下所需要的弦长,则箭体方向xb为:
xb=sinuem(t)·ε+cosuem(t)·Γ
(8)
虽然所附加的交变姿态可以在轨道面内,也可以在轨道垂面内,但对终端轨道根数的影响不同。
综上所述,对于“助推-滑行-助推”模式下耗尽关机的固体运载火箭,由于发动机提供总的视速度弧长和视位置弧长固定并满足等式(7),制导算法需要确定出合适的发动机点火时刻tig及箭体方向xb的控制指令,使终端状态矢量式(5)满足终端轨道根数式(6)的约束,以完成耗尽关机入轨任务。因此,针对耗尽关机的固体运载火箭,制导算法的本质是求解具有固定总冲约束的两点边值问题,其算法的核心则是:
1) 求解滑行点火时间,并计算满足终端约束所需速度矢量大小及方向。
2) 根据速度管控模型实现速度矢量约束,通过确定交变姿态方向实现对附加项耦合的抑制。
2 定点制导方法及拓展
固体运载火箭在大气层外飞行时,由于发动机推力脉冲大、额定时间短,无动力滑行时间通常远大于发动机工作时间,认为箭体方向始终沿着所需要的速度冲量方向[12]。因此,PA制导算法通过假设发动机持续推进过程中箭体方向xb始终保持某一常值Γ,来研究发动机完全耗尽燃料所产生的“定向速度冲量”与滑行点火时间及终端轨道根数之间的理论关系,PA算法理论如图3所示。
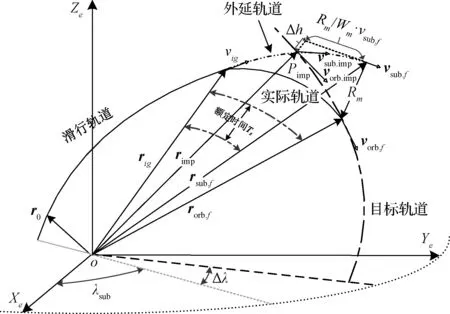
图3 PA制导算法运动分解图Fig.3 Motion analysis of pointing guidance method
图3中,r0为火箭当前时刻的地心距,rig为火箭点火时刻的地心距,rsub.f,vsub.f分别表示外延滑行轨道的额定关机时刻地心距和绝对速度,rorb.f,vorb.f表示实际飞行轨道终端地心距和绝对速度,rimp为滑行轨道与目标轨道交点处的地心距。
当运载火箭滑行-助推结束后,持续推力过程引起运载火箭动量矩的变化为:
ΔH=mf·rorb.f×vorb.f-m0·r0×v0
(9)
轨道面交点Pimp联系了两条轨道状态参数,将式(9)在轨道面交线rimp展开,详细推导过程见参考文献[11],整理后得到:
(10)
式(10)的结果表明:在特定的点火时间条件下,“定向持续推进过程”对轨迹的改变与在等效脉冲点Pimp处施加“瞬时脉冲矢量”对轨迹的影响等效。
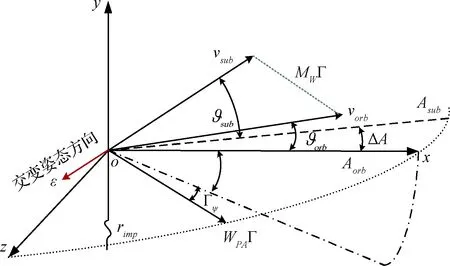
图4 轨道交点处速度矢量关系Fig.4 Vector diagram of the orbit intersection point
在轨道面交点Pimp处建立坐标系o-xyz,y轴沿着轨道面交线rimp向上,x轴沿着目标轨道速度vorb.imp运行方向且垂直y轴,z轴与x,y轴构成右手法则,则各矢量关系如图4所示,所需速度矢量Γ和交变姿态方向ε均为单位矢量,ex,ey和ez分别为x轴、y轴及z轴的单位矢量,则:
(11)
为实现固定弧长条件下的弦长问题,交变姿态速度管控微分方程组表达式为:
(12)
式中:uem(t)由交变姿态模型产生且vε=0,将式(12)代入式(5)得终端状态矢量表达式:
(13)
根据定点制导原理,将式(13)代入火箭动量矩变化量式(9)中,合并后得:
ΔH=mf·rorb.f×vorb.f-m0·r0×v0=
mf(rsub.f+rΓΓ)×(vsub.f+vΓΓ)+
mfrεε×(vsub.f+vΓΓ)-m0r0×v0
(14)
将定点制导结论式(10)代入式(14),得:
(15)
由式(15)可知:交变姿态速度管控带来的附加位置项Hem对定点制导理论产生耦合影响。此外,由于附加位置的大小受交变姿态模型的限制,因此耦合影响的程度实际上由交变姿态方向ε决定。根据图4所示,附加耦合项可表示为:
Hem=mfrε·ε×(vsub.f+vΓΓ)=mfrε·ε×
(vsub.imp+vΓΓ+Δvg·ey)=
mfrε·ε×(vorb.imp+Δvg·ey)
(16)
其中,Δvg=g·(rΓ/vΓ),将式(11)代入式(16)展开得:
Hem=mfrε(εxex+εyey+εzez)×(vorb.imp+Δvg·ey)
(17)
交变姿态方向ε在xoy面内的投影将改变入轨点地心距,为使耦合项的影响最小化,令投影矢量与速度矢量平行,即:
(εxex+εyey)×[vorb.impcosϑorb·ex+
(vorb.impsinϑorb+Δvg)·ey]=0
(18)
因此,在式(18)条件下将式(17)代入式(15)后,动量矩变化量可化简为:
ΔH=mfrimp×vorb.imp-m0r0×v0+
mfrεεz·ez×(vorb.imp+Δvg·ey)
(19)
经化简后,式(19)可表示为:
ΔH=mf(rimp+mez)×(vorb.imp+nez)-m0r0×v0
(20)
将式(20)展开与式(19)对比后,可得:
(21)
综上所述,在交变姿态速度管控的耦合影响下,定点制导理论依然适用,其结论依然成立。此时,等效脉冲点rimp.em及等效入轨速度vorb.imp.em为:
(22)
3 交变姿态速度管控算法
3.1 基底制导矢量求解
为不失一般性,将制导所需要的速度矢量表述为轨道交点地心距与终端轨道根数的矢量形式,由开普勒轨道性质得:
(23)
由于圆轨道的真近点角失去意义,故取
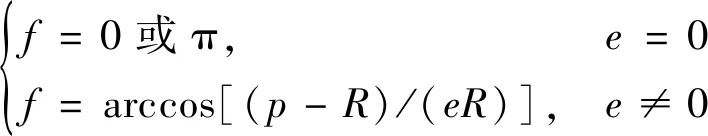
(24)
根据式(23),求解出轨道面交点Pimp处的真近点角、切向速度及法向速度。因此,图3中在两轨道交点Pimp处速度矢量表示如下:
(25)
其中,运载火箭由于当前轨道倾角与目标轨道倾角之间的偏差所引起方位角偏差ΔA的表达式为:
(26)
式中:φimp为地心距rimp的地心纬度。则PA制导所需的速度矢量大小和方向为:
(27)
在交变姿态速度管控的耦合影响下,等效脉冲点并不处于当前轨道平面内,但可认为是在轨道面交点Pimp沿z轴平移所得到,则火箭从当前点飞行至交点Pimp处的时间为:
(28)
根据式(15)和式(28)得运载火箭点火时间为:
tig=t0-imp+Ts-rΓ/vΓ-t0
(29)
由于速度矢量Γ和交变姿态方向ε为正交单位矢量,且考虑耦合项影响最小化约束式(18),则交变姿态方向ε满足:
(30)
求解式(30)可得交变姿态方向ε的表达式为:

(31)
其中,tanϑ=(vorb.impsin ϑorb+Δvg)/(vorb.imp·cos ϑorb),l为:
综上所述,通过定点制导理论及其拓展形式,基底制导矢量Γ、火箭点火时间及交变姿态方向ε分别由式(27)、式(29)和式(31)计算得到。特别地,在轨道共面即Γz=0,沿轨道面法向(平行于z轴)进行交变姿态是耦合影响最小的实现途径。
3.2 交变姿态速度管控模型
固体火箭的速度管控问题,主要是通过控制推力与所需速度矢量之间的夹角来抵消多余的速度模量。速度管控模型主要有一般能量管理方法[13](GEM)、交变姿态能量管理方法[14](AEM) 及样条能量管理方法[15](SEM)。GEM算法通过需要速度与圆心角之间的数学关系,解算得到推力方向,是一种速度闭环控制方法,但存在尾段姿态角发散的状况;AEM、SEM算法通过预先规划姿态角变化规律来实现速度管控,能够针对实际对象的模型进行细化处理,具有较大的速度耗散能力,但不能对高度进行约束。
能量管理方法其本质上均是通过交变姿态的方式实现速度管控,交变姿态模型(AEM)姿态角变化规律如图5所示,SEM方法以三次多项式来描述速度管控模型,但上述方法并未深入研究交变姿态方向的问题。因此,本文重点研究速度管控过程带来的耦合影响的抑制问题。

图5 交变姿态模型姿态角变化规律Fig.5 The variations of attitude angle respect to consumed velocity capability
发动机总视速度模量WM按照导引程序的功能分为两部分:第一部分(W0~W6),进行交变姿态实现速度管控;第二部分(W6~WM),采用定轴飞行且保持姿态稳定的方式,来避免因固体发动机秒流量大散布所带来的模型尾段姿态角速率变化过大的问题。则以视速度模量为自变量的姿态角变化模型为:
(32)
其中,WΔ=Wi+1-Wi,i=1,2,…,5。um为速度管控模型中的最大调姿角,将模型式(32)代入微分方程组(12)可得:
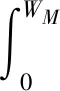
(33)
根据定点制导理论,基底制导矢量vΓ由式(27)求得,则等式(33)中仅存在的未知量为最大调姿角um,可采用一维迭代求解算法得到um的值。此外,速度管控过程中产生的位置量,通过时域内的数值积分得到,其表达式为:

(34)
其中,通过t=e-W/(Ispg0)进行换元计算。
至此,速度管控模型uem、最大调姿角um及位置量rΓ和rε分别由式(32)、式(33)和式(34)求得。对于速度管控模型,以视速度模量为自变量时,一方面有利于提高速度管控的精度;另一方面视速度模量可由加速度计积分得到,有利于提高管控模型对参数偏差及不确定性的鲁棒性。
3.3 制导算法求解流程
定点制导拓展理论证明了在速度管控耦合影响下基底制导依然适用,并得到了点火时间、所需速度矢量及交变姿态方向的解析表达式。AEM速度管控模型,根据发动机总视速度模量和制导所需速度大小得到最大调姿角,并通过数值积分得到附加位置量。综上,本文所提末级多约束自主制导方法中的未知量均已求得,详细计算流程如下:
1) 确定等效脉冲点rimp:首次计算时,忽略速度管控模型的附加位置影响,即rΓ=RM,rε=0,m=n=0,代入拓展定点制导理论式(28)计算。
2) 求解所需速度矢量Γ及交变姿态方向ε:由脉冲点处的速度矢量关系,根据式(27)计算所需速度矢量vΓ,式(31)求得交变姿态方向ε,由于交变姿态方向的两个解是对称的,可任选其一。
3) 计算最大调姿角um:根据发动机总视速度模量式(7)和制导所需的速度大小vΓ,由式(33)解算出速度管控模型中的最大调姿角um。
4) 计算附加位置分量rΓ和rε:在速度管控模型及待定系数um确定后,根据式(34)数值积分得到。
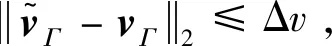
迭代循环中,由于等效脉冲点地心距rimp远大于速度控制产生的附加位置量,即rimp≫m·ez,需要非常小的阈值才能保证循环的有效迭代。因而选取变化量更为敏感的基底制导矢量vΓ为迭代变量,精度阈值Δv=1×10-3。
制导算法的点火时间、速度管控模型及交变姿态方向的迭代计算过程均处于运载火箭的无动力滑行阶段,发动机点火后的主动段则按照预先规划好的速度管控模型得到制导指令。此外,制导算法的迭代,主要用以校正速度管控附加的耦合量,整个迭代过程通常需要3~5步即可收敛。
4 仿真校验与性能评估
采用全固体火箭发动机的运载火箭,以450 km SSO典型飞行任务为例,考虑地球自旋角速度及引力J2项摄动。通过搭载不同载荷质量,验证速度管控算法的制导精度及适应性;根据不同的轨道倾角偏差,验证交变姿态方向对异面轨道任务的适应性;最后采用蒙特卡洛仿真,验证所提制导算法在模型参数偏差及不确定性影响下的制导精度及鲁棒性。
4.1 载荷质量适应性仿真
实际飞行轨迹的偏离、终端任务的调整以及卫星载荷质量的变化均要求速度管控方法对飞行任务具有一定的适应性。考虑运载火箭以200 kg为最大载荷,依次减少50 kg载荷进行仿真,直至运载火箭达到空载状态。运载火箭由于搭载不同的载荷质量,在耗尽关机方式下具有不同的速度模量,并通过速度管控模型实现终端多约束要求。为验证拓展定点制导算法对载荷质量的适应性,选取了两种典型的能量管理方法AEM和SEM进行仿真,仿真曲线如图6所示,终端偏差结果见表1。
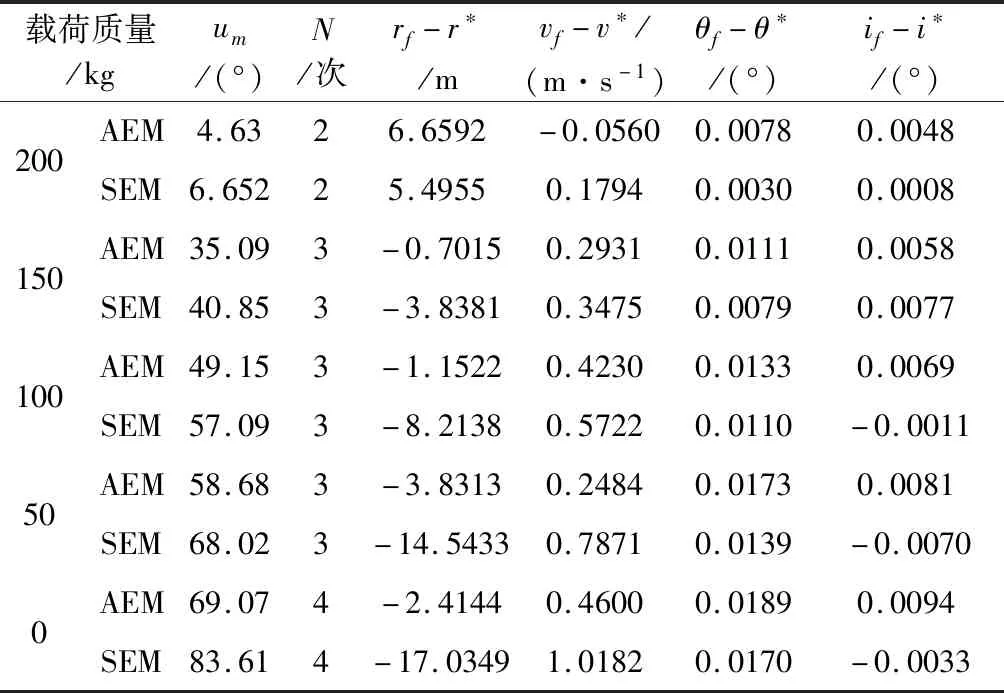
表1 不同载荷质量仿真结果Table 1 Simulation results under different load masses
注:*表示期望值,N为迭代次数。
两种能量管理方法的仿真结果见表1所示,在同样载荷质量条件下,SEM方法的最大调姿角大于AEM算法,但均能够满足0~200 kg的载荷适应范围。
两种方法在终端精度约束上均具有高精度约束能力,而SEM算法在速度大小控制上偏差量略大,达到了1.0182 m·s-1。图6中,根据不同的载荷质量,AEM方法通过控制最大调姿角来实现不同大小的速度管控,SEM方法通过求解三次多项式的系数实现不同大小的速度管控。PA拓展理论根据能量管理算法产生的附加位置量,解算交变姿态方向,在不同载荷质量条件下均能够满足终端速度、位置约束条件,实现了对速度管控中耦合项的抑制。
仿真结果表明,PA拓展理论能够适用于不同的能量管理模型,且计算的交变姿态方向能够对能量管理过程产生的附加耦合项起明显的抑制作用。此外,交变姿态方向由状态矢量在惯性空间确定,导致俯仰角及偏航角指令呈现出相互耦合的关系。
4.2 PA拓展理论对比分析
速度管控过程中产生的耦合项,一方面对脉冲点位置产生影响,改变了升交点赤经;另一方向对脉冲点入轨速度产生影响,改变了轨道倾角。通过载荷适应性仿真可知,空载条件下速度管控模型产生的附加位置量最大,故在空载条件下来验证制导算法对不同初始轨道倾角的适应性。针对PA拓展理论方法的耦合抑制方向,与文献中采用的俯仰通道[9,10,15]及偏航通道[12,16]进行对比,其结果如图7所示,终端偏差值见表2。
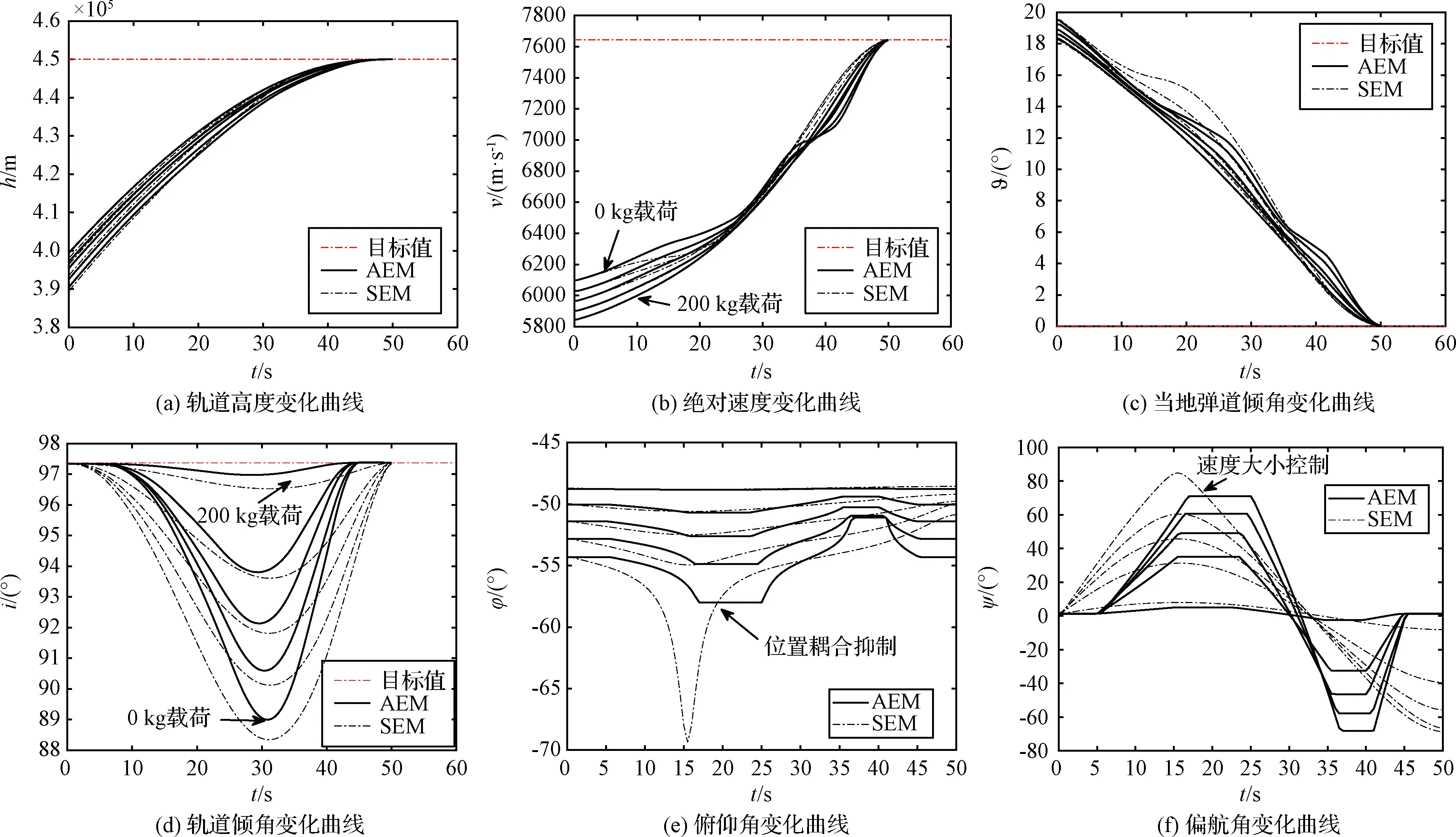
图6 载荷质量适应性仿真Fig.6 Profiles of the states run for simulation on adaptability to load masses

图7 轨道倾角适应性仿真Fig.7 Profiles of the states run for simulation on adaptability to orbit inclination angles
从图7可以看出,不同通道下的能量管理交变姿态导致轨道倾角适应性有明显的差异。采用俯仰通道进行速度管控,终端地心距将随着初始轨道倾角偏差的增大而逐渐减小,但终端轨道倾角的偏差逐渐增大,地心距的最大偏差达到14.96 km,绝对速度偏差达到7.178 m/s,轨道倾角偏差达到2.08°;采用偏航通道进行速度管控,终端地心距、绝对速度以及轨道倾角等参数将随着初始轨道倾角偏差的增大而逐渐增大:地心距的最大偏差达到3.5 km,绝对速度偏差达到1.186 m/s。仿真结果可以看出,偏航通道下偏差结果明显小于俯仰通道,但依然无法达到终端约束高精度的要求。
根据交变姿态方向表达式(31)知,由于轨道异面使Γz≠0,因而仅以轨道侧向进行交变姿态同样会对轨道面内的参数产生影响,主要原因是速度管控产生的耦合项改变了原等效脉冲点及需要速度。而采用PA拓展理论在ε方向进行速度管控,使终端地心距、绝对速度及轨道倾角等参数因耦合引起的偏差得到了有效的抑制。

表2 轨道倾角适应性仿真结果Table 2 Simulation results under different orbit inclinations
4.3 制导精度与鲁棒性分析
以小型固体运载火箭进入450 km预定太阳同步轨道为例,验证本文所提固体火箭多约束制导方法的制导精度及鲁棒性。模型的不确定性及散差分布配置见表3,偏差散布及不确定性对飞行轨迹的影响以导航输入的方式提供给制导算法,制导周期取20 ms在线解算制导指令。各项随机偏差在每次打靶中随机产生,且服从正态分布。进行2000次蒙特卡洛仿真,仿真抗干扰轨迹曲线簇如图8所示。

表3 蒙特卡洛仿真散差配置表Table 3 Dispersions in Monte Carlo simulations
图8中,在所配置的偏差干扰下,轨道根数的变化曲线簇的宽度表征了制导算法的鲁棒性。结果表明半长轴偏差的数学期望值小于100 m,偏心率的散布达到10-4量级,轨道倾角达到10-4(°)量级。因此,本文所提制导算法对终端轨道半长轴、偏心率及轨道倾角具有高精度约束能力的同时对所配置的偏差干扰具有强鲁棒性。2000次蒙特卡洛终端轨道根数仿真统计结果见表4,轨道根数偏差散布如图8 (d) 所示。
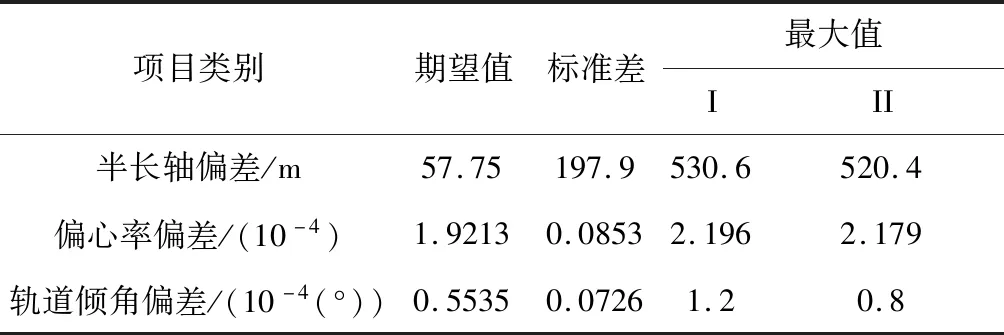
表4 终端约束蒙特卡洛仿真洛统计结果Table 4 Monte Carlo simulations statistic results
5 结 论
1) PA拓展制导算法在定点制导理论的基础上,进一步根据速度管控产生的耦合项得到等效矢量关系,推导出点火指令与推力矢量的求解方程,具有耗尽关机终端多轨道要素的约束能力。
2) 传统的俯仰通道、偏航通道下的能量管理方法,并未考虑耦合产生的影响,对于共面圆轨道条件该方式影响较小,但对于异面椭圆轨道,耦合项将导致终端约束无法满足。
3) 本文所提制导算法,对不同的载荷质量具有很强的适应性,速度管控对耦合项具有较强的抑制能力,对所配置的干扰源具有很强的鲁棒性。
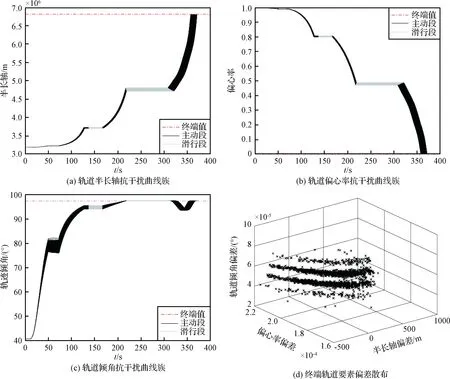
图8 蒙特卡洛仿真轨道根数变化曲线簇Fig.8 Profiles of the orbital elements run for Monte Carlo simulation
