毕达哥拉斯定理证明2500年的文化史趣谈①——以E.S.Loomis的《Pythagorean Proposition》为例

张冬莉 代 钦

(内蒙古师范大学科学技术史研究院 010022)

卢米斯(E.S.Loomis,1852—1940)，是美国俄亥俄州的数学老师，他用毕生精力来收集所有已知的毕达哥拉斯定理的证明方法，并整理出版了著作《Pythagorean Proposition》，其中收录了367种证明方法.该书的初稿是在1907年完成.1927年初版，1940年第二版.1986年全美数学教师委员会重印了这本著作，这是数学教育领域中第一部“传世之作”.后来卢米斯又收到许多新的证明，但他没有补全汇编.至今为止，毕达哥拉斯定理的证明方法已经达到500多种.

卢米斯(E.S.Loomis,1852—1940)

1 前言

毕达哥拉斯定理是一个著名的定理，被誉为“几何中的瑰宝”.在历史上称为“第47个命题”，这是源于欧几里得的《几何原本》的第47个命题.由于它在三角学、测量术、导航和天文学等领域的广泛应用，使它成为平面几何中最基本且最有趣的定理之一.在数学文献中被各种各样的命名，如它被称为“木匠定理”；又由于它的证明灵活、困难而被称为“傻瓜的桥梁”或者“愚人之桥”；在法国它被称为“驴桥定理”；在中世纪，这个定理也被称为“百牛定理”，据说这是毕达哥拉斯为了庆祝这伟大的发现，宰了一百头牛来祭奠.关于毕达哥拉斯的具体证明方法我们仍然不知道，毕达哥拉斯本身是否发现了这个直角三角形的这个特征，还是从埃及神父或者从巴比伦学习到的，也没有公认的说法.根据最广泛的流传，毕达哥拉斯从埃及神父那里学习到了三角形的特征，出于这个原因，三角形本身也被命名为埃及三角形或毕达哥拉斯定理.

勾股定理是我国古代数学的一项伟大发现，因此毕达哥拉斯定理在中国称为“勾股定理”.勾股定理最早出现在《周髀算经》中.《周髀算经》原名《周髀》，约成书于公元前2世纪西汉时期，书中涉及数学、天文知识等.《周髀算经》主要成就是分数运算、勾股定理以及天文测量中的应用，其中关于勾股定理的论述最为突出.《周髀算经》中周公和商高，以对话形式给出勾股定理.三国时期吴国人赵爽为《周髀算经》作注，其中赵爽的“勾股圆方图”是运用数形结合的思想方法——“等面积原理”，给出了勾股定理的证明.

2 367个证明中一些著名的证明方法及其特征

除了像欧几里得(Euclid)、莱布尼兹(Leibniz)、赫顿(Hutton)、加菲尔德(Garfield)、惠更斯(Huygens)等这样著名的数学家为定理的证明做出贡献以外，其他不同阶层的人员，比如一些高中数学老师，大学数学教授和天文学教授，或者是坐在扶手椅上的老年哲学家，还有战壕里的年轻战士，都在为毕达哥拉斯定理的证明寻找方法而耗去时光.可见这条定理是多么地吸引人.

在收集的367个证明中，有的十分精彩，发人深思；有的十分简洁，耐人寻味；有的因为证明者身份特殊而非常著名.我们将毕达哥拉斯定理的论证方法主要分四种，第一种是线性关系的代数证明，例如，从类似直角三角形的线性关系可以证明直角三角形的斜边的平方等于其他两边的平方和；可以借助使用一个圆或者两个圆，利用弦、割线和切线的方法证明定理；还可以通过相似三角形的性质、面积的比、极限的理论、代数几何的综合法证明定理.第二种是几何证明，可以通过三个正方形构建在外部或者内部的不同情况，例如，三个正方形构建在外部、三个正方形都在内部等十种形式进行分类，利用等面积转换法证明，所有几何证明的结果都来自区域的比较，其基本原理是叠加.后来又根据操作原理分成了第三和第四种：“向量证明”和“动态证明”.

2.1 代数证明

2.1.1法国数学家勒让德(Legendre，1752-1833)——最短的证明

如图1所示，在直角三角形ABH中，作HC⊥AB，直角三角形ABH，ACH和HCB相似.为了表示方便，分别用a，b，h，x，y和h-y代表BH，HA，AB，HC，CB和AC.因为通过三个三角形相似，可以得到三边的比例关系.一共可以写出9个等式：

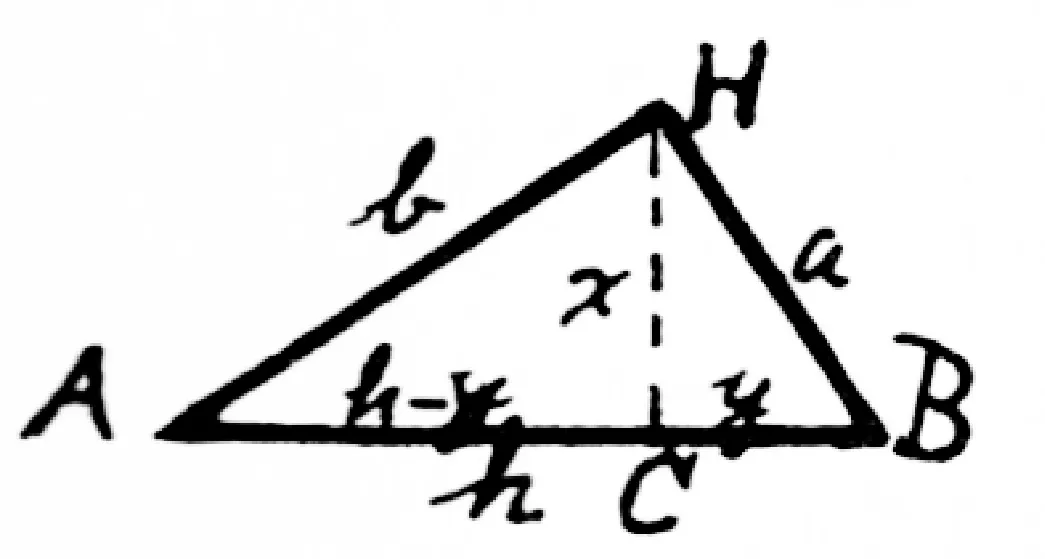
图1

(1)a∶x=b∶h-y,∴ah-ay=bx；

(2)a∶y=b∶x,∴ax=by；

(3)x∶y=h-y∶x,∴x2=hy-y2；

(4)a∶x=h∶b,∴ab=hx；

(5)a∶y=h∶a,∴a2=hy；

(6)x∶y=b∶a,∴ax=by；

(7)b∶h-y=h∶b,∴b2=h2-hy；

(8)b∶x=h∶a,∴ab=hx；

(9)h-y∶x=b∶a,∴ah-ay=bx.

从上述的九个等式中，没有一个方程可以确定所需要的关系，但是可以由(5)和(7)两个等式组合，就能得到h2=a2+b2.这应该是毕达哥拉斯定理的最短的证明，通过两个等式即可完成.

2.1.2莱布尼兹(Leibniz,1646-1716)的证明方法

如图2，如果(1)HA2+HB2=AB2，然后(2)HA2=AB2-HB2，由此(3)HA2=(AB+HB)·(AB-HB).取BE，BC的长度等于AB，以B作为圆心画半圆CA′E，连结AE，AC，作BD垂直AE.现在有(4)HE=AB+HB，(5)HC=AB-HB，(4)×(5)可以得到HE×HC=HA2，当△AHC与△EHA相似的时候，以上的结论才是正确的.

图2

∴(6)∠CAH=∠AEH，(7)HC∶HA=HA∶HE；因为∠HAC=∠E，然后∠CAH=∠EAH，∴∠AEH+∠EAH=90°，∴∠CAH+∠EAH=90°，∴∠EAC=90°，∴顶点A在半圆上，A与A′重合，∴△EAC在半圆内且是一个直角三角形.由于方程(1)可以导出数量关系是直角三角形，然后从这样的三角形，转换到我们的论点就有h2=a2+b2.

三角形与圆有着密切的联系，每个三角形都有一个外接圆和一个内接圆.莱布尼兹的证明方法主要是构造辅助圆的证法.

2.1.3赫顿(Hutton，1726-1797)的证明方法

∴h2=a2+b2.

图3

该证法中，AD正方形实际就是我国《周髀算经》中的“赵爽弦图”.弦图是以弦为方边的正方形，再在其内作四个全等的勾股形，各以正方形的边为弦.赵爽称勾股弦形的面积为“朱实”，称中间小正方形的面积为“黄实”或“中黄实”.

2.1.4书中第101个代数证明

如图4，让AD=AG=x，HG=HC=y,BC=BE=z,然后AH=x+y，HB=y+z.以A为中心，AH为半径画弧HE，以B为中心，BH为半径，画弧HD，以B为中心，BE为半径画弧EC，以A为中心，AD为半径，画弧DG.然后画出平行线.通过观察这个数字，就可以明显看出如果y2=2xz(1)AH2=AR×AD=(x+y)2=x·(x+2y+2z)=x2+y2+2xy=x2+2xy+2xz=y2=2xz，那么定理就成立了. 现在，因为AH是一个切线，AR是同圆的一个弦.AH2=AR×AD(切割线定理)，或(x+y)2=x(2y+2z)=x2+2xy+2xz，因y2=2xz，

∴正方形AK=[(x2+y2+2xy)=正方形AL]+[(z2+2yz+(2xz=y2))]=正方形HP，

∴h2=a2+b2.

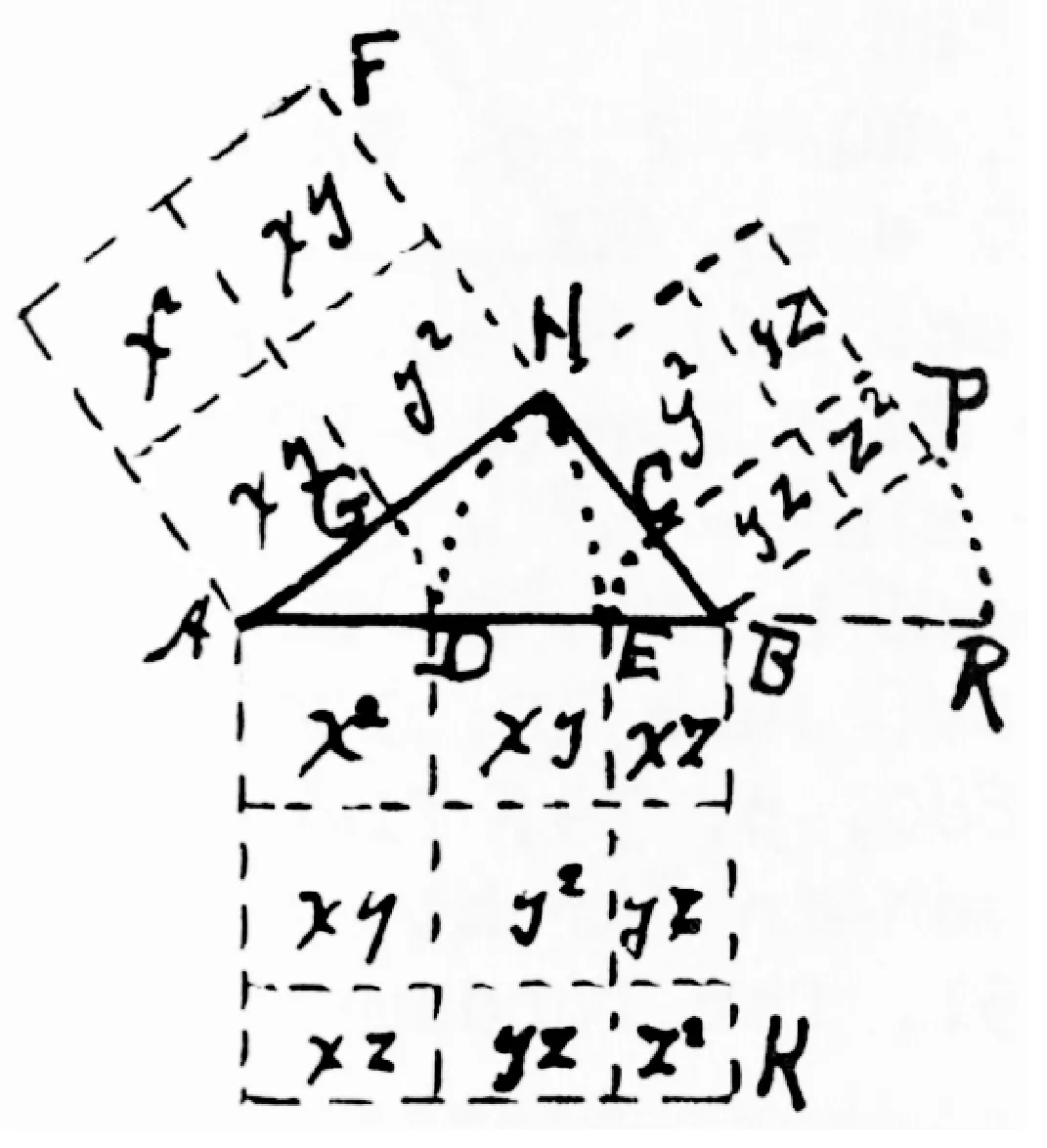
图4

从三边分别向外作正方形，并进行分割，将各个小矩形块的面积写其内部.再构造辅助圆的证法，使用切割线定理证明.这个证明是几何灵活性的一个很好的例证.其价值在于，不是在多次确立的事实上重复证明，而是需要更好的洞察力，在证明元素的有效编组和使用中，呈现出各种几何定理的相互依赖和转化.

2.2 几何证明

2.2.1欧几里得(Euclid，约公元前330年-约公元前275年)的证明方法

如图5，作HL垂直CK，连接HC，HK，AD和BG，AB的平方=矩形AL+矩形BL=2三角形HAC+2三角形HBK=2三角形△GAB+2三角形△DBA=正方形GH+正方形HD，∴AB上的正方形=BH上的正方形+AH上的正方形.

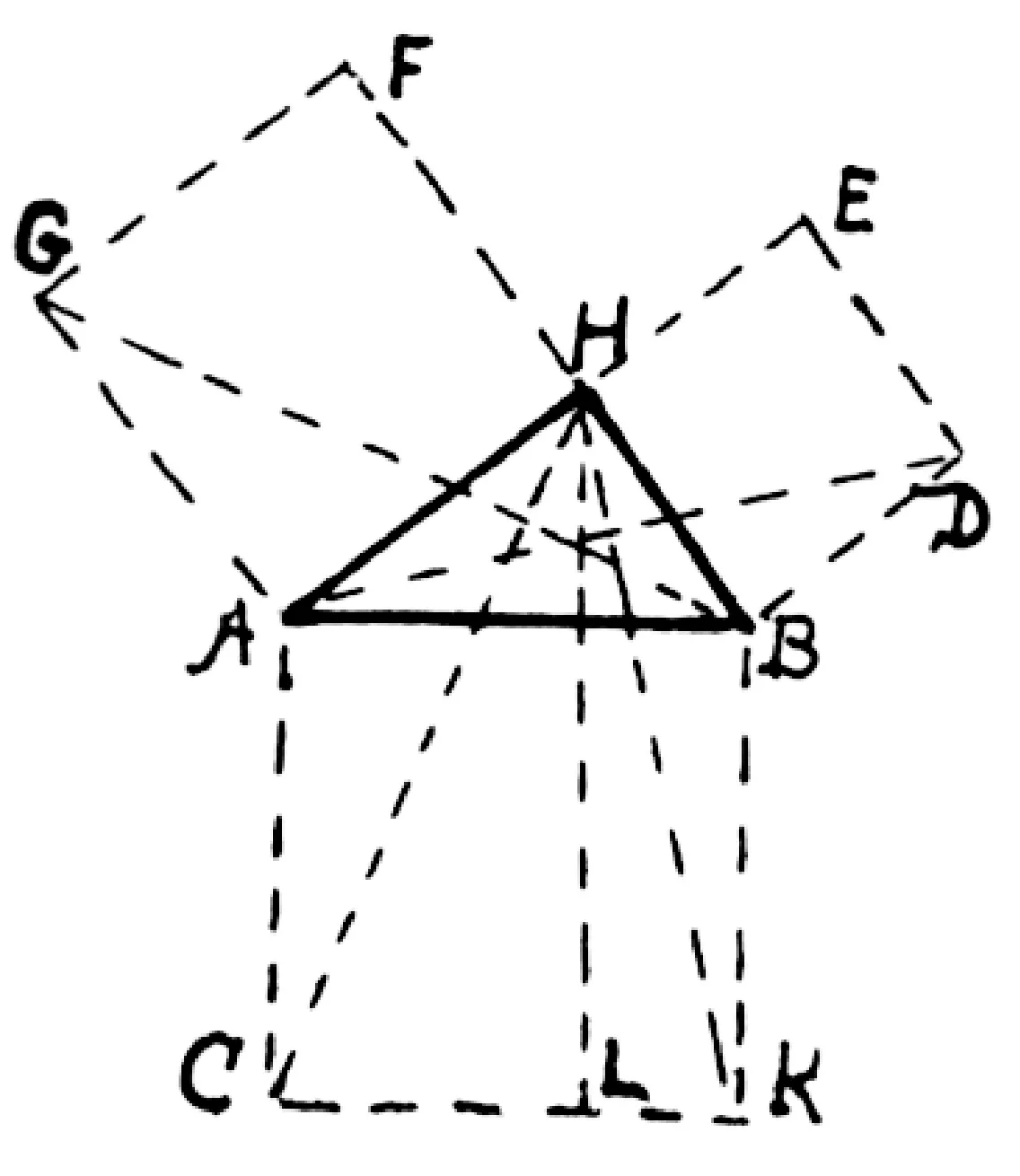
图5

该方法是几何证明里的第33个证明.欧几里得采用的是分析法，大约公元前300年，发现了上述证明，从逻辑上讲没有比欧几里得更好的证明.该证明也反映了古希腊人的分析思维方法.

2.2.2惠更斯(Huygens，1629-1695)的证明方法

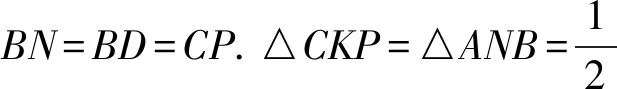
图6

2.2.3苏格拉底(Socrates，公元前469-公元前399年)的证明方法

所谓的毕达哥拉斯定理，最简单的形式就是两条直角边相等.伟大的苏格拉底通过画图让奴隶孩子回答问题.将他的木棒作为指南，在地上画图，使奴隶孩子看到了三角形HAB中，HB边上的正方形与HA边上的正方形的和，正好等于AB边上的正方形.如图7所示.

图7

该图形并不是苏格拉底给奴隶孩子讲解的原图，而是将原图进行了转化.苏格拉底的这种证明方法和他的用两个相同正方形制作一个大正方形的思想方法有着密切关系.苏格拉底用“产婆术”指导求出新正方形的方法，除了对一般教学法有重要启示以外，对数学教学也有重要的借鉴作用.例如，我们把问题倒过来说就是：用两个相同的正方形构造一个新正方形．我们将问题变化为：能否用两个不同正方形构造一个正方形？答案是肯定的，由勾股定理直接可以引证：a2+b2=c2，即两个正方形面积之和等于第三个正方形的面积.可以用古希腊数学家欧几里得的证明方法或中国古代数学家刘徽的证明方法直观地表达出来，也可以用折纸方法(或实验几何方法)进行制作.

如果把两个不同正方形当做一般情形的话，那么前面的问题就是其特殊情形.我们进而可以提出：能否用n个相同(不相同亦可)的正方形构造一个正方形吗？答案也是肯定的，可以用数学归纳方法来说明.据了解，现实数学教学中存在的问题是，初中数学教师教授勾股定理时，从来不考虑学生在小学所学相关平面图形知识，更不考虑勾股定理的实验几何特性及其扩展(2)代钦.可视的数学文化(三)——苏格拉底的数学教学智慧[J].数学通报，2016，55(08):3-4..

2.2.4美国总统加菲尔德(Garfield，1831-1881)的证明

1876年4月1日，加菲尔德(3)Garfield J A.Pons Asinorum.New England J Educ，1876，3(161)在《新英格兰教育日志》上发表了证明勾股定理的方法.

如图8所示，延长HB到点D，使得BD=AH，过D点作DC平行于AH并且等于BH，然后连接CB，CA.

梯形CDHA的面积=△ACB+2ABH.

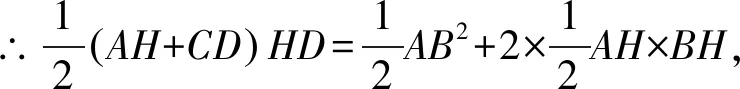
∴h2=a2+b2

图8

2.2.5毕达哥拉斯定理——神奇的魔方

如图9，AK正方形中，所有的数字和是625，等于HD正方形中数字的和441加上HG正方形中数字的和184.在AK正方形中间数为25，有1×(1×25)；周边小正方形的数字和为3×(3×25)；选取大正方形AK中的数字和为5×(5×25)的数字作为元素.正方形HD中有1×(1×49)；3×(3×49)，作为元素.HG正方形中有1×46和3×46作为元素.

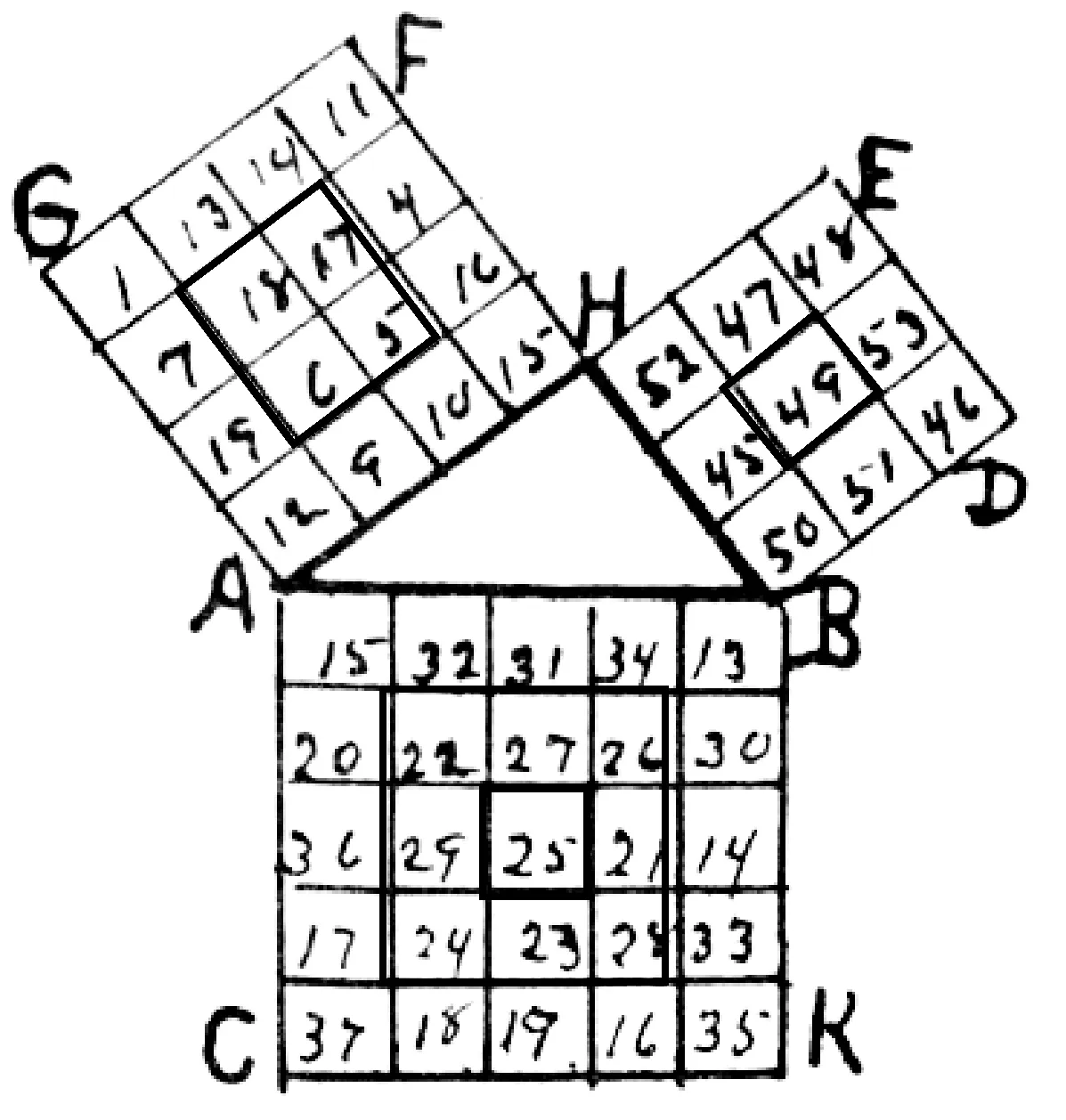
图9

该证明方法我们可以称它为“数字游戏”.在特定边长为“3,4,5”的神奇的正方形中，编入特定的数字，我们可以发现AK正方形中所有数字和等于HD正方形中数字和加上HG正方形中数字的和.正方形AK的任意一行、一列和两条对角线上的数字总和均为125，因此总和为625.正方形HG的每一行、每一列和两条对角线上数字和均为46，正方形HD的则为147，因此，HG里所有数的和是184，HD里所有数的和是441.因此，魔方AK(625)=魔方HD(441)+魔方HG(184).

2.3 向量的证明

向量的发展大致分为三个阶段：首先是实例中的向量，用平行四边形法则得到力的合成，在此阶段，向量仅仅是物理力学的一个应用,并没有形成一门独立的学科,更没有受到重视.其次为分解向量阶段，力的分解是无法靠加减乘除的运算进行的,这样就引入了新的运算——“数乘”.最后一个阶段，向量中引入“数量积”.

如图10，完成矩形HC，连接HC.矢量AB=AH+HB或者a=b+g(1)，HC=HA+AC，或者a′=-b+g(2).则(1)的平方加上(2)的平方有a2+a′2=2b2+2g2，或者看作AB2+HC2=2AH2+2HB2，但是HC=AB，∴AB2=AH2+HB2，∴h2=a2+b2.

图10

2.4 基于力的概念——动态证明(符合“力偶矩”(4)力偶是两个相等的平行力，它们的合力矩等于平行力中的一个力与平行力之间距离(称力偶臂)的乘积，称作“力偶矩”.的理论)

如图11，如果FH和AG代表两个相等的力，它们形成力偶矩FH×AH，或者b2.如果HE和DB代表另外两个相等的力，它们形成力偶矩DB×HB，或者a2.

图11

存在这样的两对力.即加入两个力AG和HE,使得AM=HE=a，AG和AM的两个力的合力为平行四边形的对角线AN，AN=CA=h.加入FH和DB两个力，使得BO=DB=a，即平行四边形的对角线BK是BO和BP的合力(BP=FH=b)，力偶矩的第二个分量就是CK×BK，或者h2. ∴h2=a2+b2.

3 为什么没有利用三角函数、解析几何、微积分的方法证明勾股定理

通过之前的证明方法，有的人会提出这样的问题，十七世纪，变量数学问世之后，有没有基于三角函数、解析几何和微积分的证明呢？答案是没有这类的证明方法.因为三角函数的基本公式本身就是毕达哥拉斯定理的真理，因为这个定理，我们说sin2A+cos2A=1.

例如：如图12，在直角△ABC中，∠C=90°，AB=c,BC=a,AC=b.

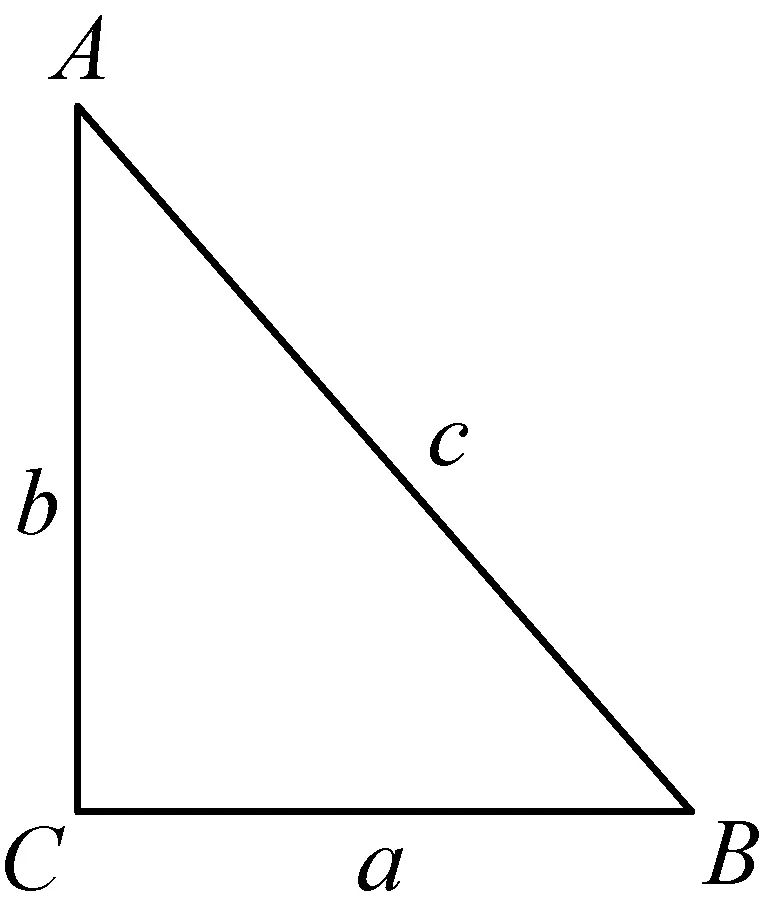
图12

因为a=c·sin∠A,b=c·cos∠A,(sin∠A)2+(cos∠A)2=1，

a2+b2=(c·sin∠A)2+(c·cos∠A)2

=c2[(sin∠A)2+(cos∠A)2]=c2,

所以a2+b2=c2.

该证明是错误的.观察这个证明方法，从结论开始检查每一步证明，似乎没有错误.那么问题究竟出在哪里呢？具体情况主要是因为(sin∠A)2+(cos∠A)2=1是勾股定理的特殊形式，不能做条件来使用.这里犯了循环论证的错误.

在解析几何中，笛卡儿把勾股定理作为他的解析几何方法的基础，所以在这里不会出现独立的证明.解析几何是以代数方法处理的欧几里得几何学，因此涉及的解决方法，都是已经建立的原理.因此，在解析几何中关于直角三角形三边的关系，都直接暗含着毕达哥拉斯定理，如公式：x2+y2=r2.

4 小结

没有哪个几何定理能够像毕达哥拉斯定理的简单二次公式那样，对其他数学分支产生如此多的影响.的确，古典数学和现代数学的大部分历史都是围绕着这个定理而写成的(5)[英]M. I.芬利.The Legacy of Greece [M].张强，译.上海：上海人民出版社，2016:95.一些古老重要的数学工作都有着永恒的品质，就像任何领域的经典.作为数学中两大瑰宝之一的毕达哥拉斯定理，贯穿在整个古代和中世纪两个漫长的历史时期中，到今天仍不失其价值.它是人类发现的第一定理、第一个不定方程、证法最多的定理.它引发了第一次数学危机，开始把数学由计算与测量的技术转变为论证与推理的科学.

对于刚刚开始学习几何的学生来说，勾股定理的证明是他们遇到最难的证明之一.现在的中学数学教学中由于几何证明的直观性，在学习定理时经常使用几何证明方法便于学生理解.但是勾股定理的教学仅仅让学生知道结论并会套用是远远不够的，应让学生通过勾股定理的学习更好地掌握数学思想方法、激发学习兴趣、培养探索精神、经受历史的熏陶.除此之外，使用拼图的方法也广泛使用，注重培养学生动手操作能力.在教学中通过设计探究活动，使勾股定理的教学成为再创造和再发现的教学，进而发展学生发现、提出问题与分析、解决问题的能力.另外勾股定理的变式，即在可变倾斜的三角形的三边上构建正方形也应该值得我们的关注，有利于培养学生思维的灵活性.总之，证明定理的方法和数量并不是仅限于此，代数、几何证明的数量是无限的.以上方法的归类，可以有助于新知识的产生，吸引着未来的研究人员不断的探索.

致谢：本文原始文献E.S.Loomis《Pythagorean Proposition》在我国买不到的情况下，日本数学教育家松宫哲夫教授赠送了该书.这里表示衷心感谢！