机场新增卫星厅对中转旅客影响的研究

刘兴芬，王利平，李 强，邓 卫

(湖南大学 a. 数学与计量经济学院， b. 化学化工学院， c. 机械与运载工程学院，中国 长沙 410081)

近年来，随着社会经济的快速发展，国民收入水平不断提高，旅游业已逐渐成为我国重要产业。旅客数量的迅速增长，使现有的民航资源正面临着日益严峻的考验。很多航空公司在机场的现有航站楼运载量已远不能满足旅客高效出行和航班转场需求。为了缓解客流量快速增长和飞机转场时登机口不足的压力，新扩增卫星厅是主要方法。从资源节约角度考虑，一般航站楼具有完整的国际机场航站功能，卫星厅只作为航站楼的延伸，可以候机，却没有出入境手续办理功能。随之也将对中转旅客的航班衔接带来负面影响。新增的卫星厅造成机场管理的复杂性明显增加，部分中转旅客的航班衔接时间被扩大，导致旅客中转失败的可能性增加。如果管理不当，可能会发生航班无法降落，导致飞机延误，产生多米诺骨牌效应等。因此，优化分配登机口，减少中转旅客的换乘时间，进一步提高机场的服务质量具有重要的现实意义。

目前，国外很多学者对登机口分配问题进行了较深入的研究，其中解决的方法主要包括关键路径法、分支定界法、整数规划法、系统仿真、专家系统、启发式算法、网络流及多目标规划等。最近几年更倾向于用启发式算法进行求解。2018年杨顺秀[1]建立了面向航班延误情景的登机口调度多目标模型，并设计了扩展的人工雨滴算法进行求解。2015年，陈骁睿[2]统筹了机场运行效率和乘客服务质量，详尽地研究了登机口调度问题的关键因素及约束条件。Yu和Lau[3]以最小化中转乘客步行距离和最小化错过并后续转乘其他航班的乘客数量为目标，建立了侧重于中转旅客满意度的登机口再分配模型，并提供了一种启发式方法求解该模型。Marinelli等[4]研究了基于蜂群优化(BCO)的元启发式方法来求解登机口分配问题；2016年Dorndorf和Jaehn等[5]采用图论中团划分方法建立了登机口分配冲突最小化模型，并提出回收规划程序进行求解。2017和2019年Stollenwerk等[6,7]采用D-Wave量子退火方法研究模型的可解性，在有一定限制的量子退火条件下使得登机口分配问题得到解决。2017年，Schaijk等[8]提出了一种将确定性登机口约束替换为随机登机口约束的新方法来提高登机口分配模型(Fgap)解的鲁棒性。Dell等[9]研究了基于模糊蜂群优化(FBCO)的元启发式方法来求解登机口分配问题。Zhang等[10]针对恶劣天气、航班延误和航班取消等情况，对纯登机口再分配问题和带连接乘客的登机口再分配问题建立了两种多商品网络流模型，并分别提出潜水启发式算法和滚动层算法进行求解。2018年Pternea等[11]提出了带有乘客航班连接的登机口改进多维度重新分配模型，并嵌入到基于数学规划的启发式算法中进行求解。Pineda等[12]研究了一种结合DEMATEL，DANP和VIKOR方法的混合模型，帮助航空公司管理人员在机队调度干扰中对最合适的飞机类型进行排序和识别。

单纯的航班—登机口的优化分配问题已被很好地解决[13]，但在优化分配登机口的同时考虑航站楼的类型并最小化旅客换乘时间，目前鲜有研究。假设航站楼和卫星厅分别有m1和m2个登机口，其中登机口又分为窄体机和宽体机、国内和国际、到达和出发等几种基本属性及类型，每个登机口的功能属性事先给定，不能改变，航班只能分配到与之属性相吻合的登机口，且每架飞机转场的到达和出发两个航班必须分配在同一登机口进行，其间不能挪移别处。本文主要考虑新增卫星厅的前提下，加入中转旅客换乘时间及其紧张度等因素对航班—登机口分配问题作进一步研究与优化。

1 模型与方法

考虑一般航班—登机口分配，尽可能多地分配航班到合适的登机口并且在此基础上最小化被使用登机口的数量：

且s(n)≤n，其中：

定义：

则有

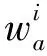
每架飞机只能被被分配到一个登机口，即

对于被分配到同一个登机口的两个相邻航班应该满足后一个航班的到达时间与前一航班的出发时间相隔至少是45 min，即

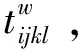
并使得旅客的总体最短换乘时间尽量小

其中pk为需要从航班i中转到航班j的人数。

假设某旅客中转成功，则其最短流程时间tijkl，否则惩罚其最短流时间tijkl=360 min。加上换乘旅客自身因素，需要考虑换乘旅客总体紧张度尽量最小化，

则完整目标及约束可概括为以下线性多目标规划模型

2 求解算法

2.1 航班—登机口分配规则

图1 航班到达时间和出发时间分布图Fig. 1 The distribution of flight arrival time and departure time

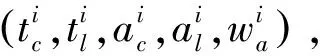
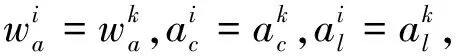
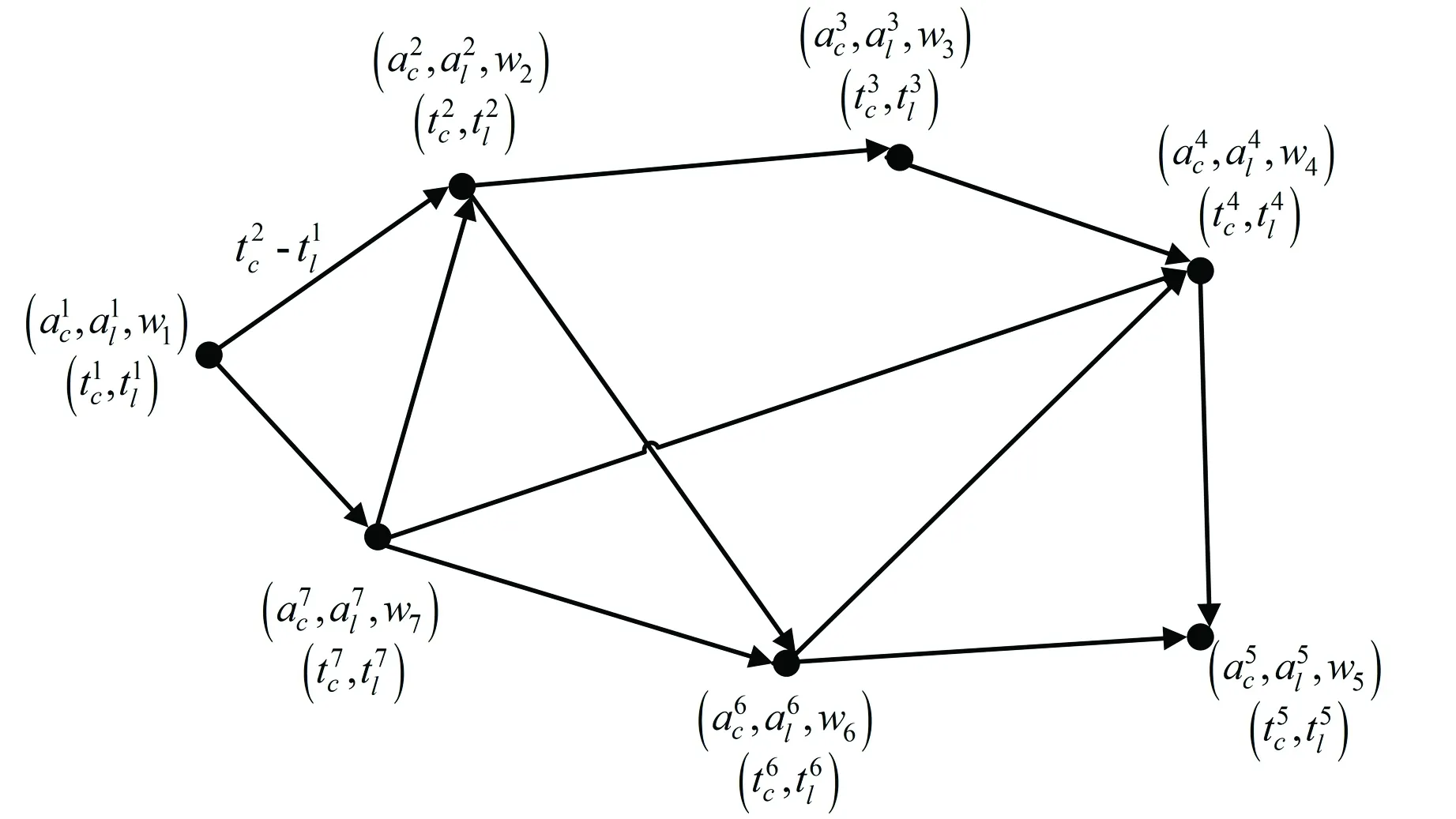
图2 有向赋权图Fig. 2 Directed weighting graph

其算法流程如下。

Step 3：重复step2直到找不到满足条件的航班，则j=j+1，若j≤m，转到2；否则，停止。

2.2 多目标处理

通过选取不同登机口的初始位置作为初值，利用以上算法可得到在目标函数(1)下基于不同初始位置的若干可行解，还应使得旅客总体换乘时间紧张度以及被使用登机口的数量最小化。取可接受目标(1)，引入层次分析法进行综合评价，选取最优初始值及最优方案。其一般步骤如下：

① 构造两两比较的判断矩阵；

本文基于目标(1)下旅客总体紧张度(N)、换乘时间(T)、被使用登机口的数量(Y)递减的重要性构造判断矩阵如下表1下：

表1 判断矩阵

② 由判断矩阵计算各指标对于该准则的相对权重，并进行判断矩阵的一致性检验；

③ 计算各层次对于系统的总排序权重。

一致性检验的步骤如下。

(1)计算一致性指标CI：

(2)查找相应的平均随机一致性指标RI，计算一致性比例CR：

当CR<0.1时，认为判断矩阵的一致性是可以接受的，否则应对判断矩阵作适当修正。

其一致性比例为0.007 9，最大特征值为3.009 2，因此该判断矩阵通过了一致性检验，且所计算的相对权重理论上正确。由此可得到旅客总体紧张度(N)、换乘时间(T)、被使用登机口的数量(Y)综合权重(w1,w2,w3)=(0.539 6，0.297 0，0.163 4)：

min(w1N+w2T+w3Y)。

从而确定最优登机口分配方案。

3 实证分析

3.1 数据选取

本文实例选取2018年“华为杯”研究生数学建模竞赛F题，取材于中国东方航空公司和上海浦东国际机场，飞机转场计划和中转旅客信息包含2018年1月19，20和21三天的数据。为了简化问题，本文只对20日到达或20日出发的航班和旅客进行分析，得到303条有效的飞机转场记录和1 677条中转旅客记录，其中包含了597架次航班，包括国内/国际、到达/出发、宽体机/窄体机等功能属性及69个登机口的各属性，其中航站楼和卫星厅分别有m1=21,m2=48个登机口。

本题数据中使用到的宽窄飞机型号分别有：

宽体机(Wide-body)：332， 333， 33E， 33H， 33L， 773；

窄体机(Narrow-body)：319， 320， 321， 323， 325， 738， 73A， 73E， 73H， 73L。

3.2 结果分析

采用上述算法，取λ=μ=1，得到最优分配方案有252架次飞机被成功分配到固定登机口，成功率为83%，还剩3个宽类型的登机口未使用。针对1 677条中转旅客总体紧张度为421.56，总体换乘时间为78 195 min，约1 296.9 h，登机口的总体使用率为60.3%，其各登机口使用率如下表 2所示。

表2 登机口使用率

进一步分析可知：

(1)如表 3所示，宽体飞机和窄体飞机成功分配到固定登机口的成功率有显著差异，通过对窄体机和宽体机登机口对比，发现窄体机登机口和相匹配的航班数比为11∶1。根据表3，宽体机仅为2.17∶1。由此可见窄体机飞机架次相对较多，可供分配的登机口资源匮乏导致成功分配到固定登机口的成功率较低，应该适当增加窄体机登机口。

表3 航班匹配情况

(2)如图3所示，最大换乘时间为81 min，最小为25 min，相应旅客两次乘坐航班都是国内，且不需要乘坐捷运办理手续，换乘时间由15 min最小流程时间加10分钟最小行走时间构成。旅客换乘时间大部分集中在30～40 min，50～60 min，65～75 min。进一步分析发现，换乘65～75 min比例较多，这类旅客的情况是乘坐国际航班降落卫星厅S并换乘在S起飞的国际航班，中间需要乘坐两次捷运，表明卫星厅S对国际航班旅客的影响更大，进一步验证了算法的合理性。

(3)最大紧张度为0.859，如图4可直观地看出旅客紧张度总体偏小，从表4可看出95%的旅客紧张度都可以控制在0.6以内，也从侧面反映了模型和算法的可靠性。

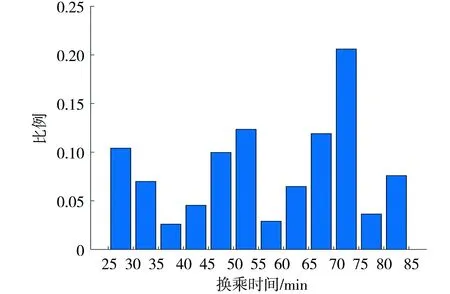
图3 旅客换乘时间比例分布Fig. 3 Proportional distribution of passenger transfer time

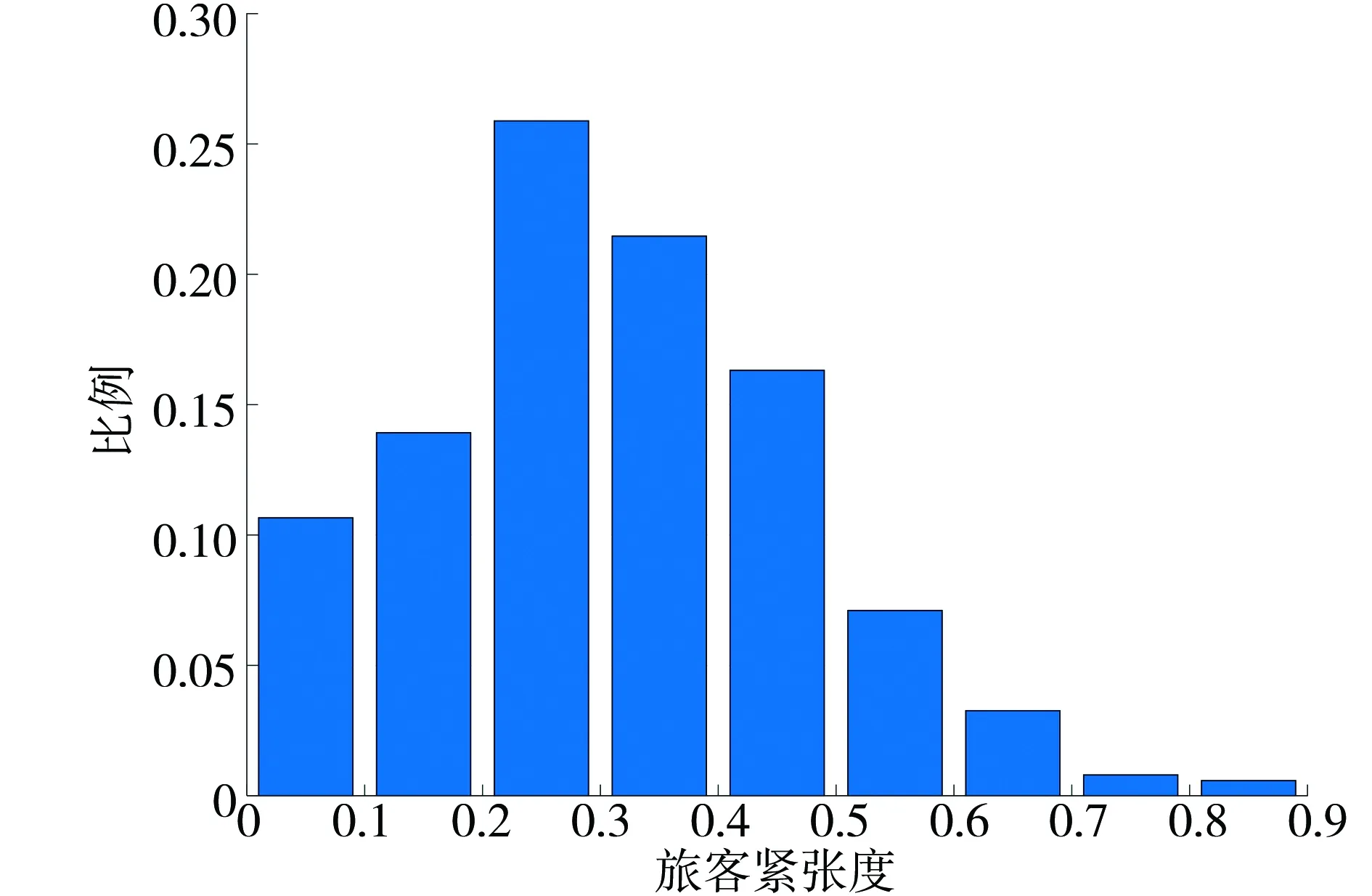
图4 旅客紧张度比例分布Fig. 4 Proportional distribution of passenger tension

表4 旅客紧张度比例分布

4 结论

本文基于多目标规划构建了航班登机口分配优化模型，通过将问题抽象化，赋予不同的航班到达时间权重λ与停留间隔时间权重μ为基准，模拟结果表明基于Dijkstra算法思想改进的启发式贪心算法具有较高稳定性，再结合层次分析法对其余目标进行综合评价，通过一致性检验，使航站楼与新增卫星厅的登机口分配问题得到有效解决。通过算例验证了利用该模型和算法得到的结果与实际情况相符合，直接证明了其可靠性。