机场登机口分配问题的顶点着色模型与算法
2021-05-25梁超超陈培军
梁超超,陈培军
(太原科技大学 应用科学学院,太原 030024)
随着旅行业快速发展,机场航班日起降架次的增多和乘飞机出行人数的迅速增长,现有的登机口资源正面临着越来越严峻的考验。在航空运输管理中,机场管理处于重要地位。在机场管理中,航班机位(即登机口)分配处于重要地位。针对航班-登机口分配问题,文军和孙宏[1]等提出了一种登机口分配问题的排序模型,并采用登机口标号函数建立标号算法对其进行求解。田晨和熊桂喜[2]通过运用遗传算法来求解航班-登机口分配问题。文军、李冰[3]等人提出了一种登机口分配问题的图着色模型,并通过时间片算法确定航班使用登机口的时间冲突集合,根据“先到先服务”的原则建立登机口分配的顶点序列着色算法。
但很多现有航站楼的旅客流量已达饱和状态,为了应对与日俱增的运营压力,正增设卫星厅。2018年“华为杯”第十五届研究生数学竞赛F题对这类问题的登机口分配提出了研究要求。航站楼T和卫星厅S的布局设计如图1所示。航站楼T有28个登机口,卫星厅S有41个登机口,具体数据见赛题。航班分配问题的任务可理解为在尽可能节约资源的情况下,给出能够有效分配最多的航班到适合的登机口的问题。由于登机口与机型的约束,以及航班与航班之间存在时间冲突,可将问题转化为带约束的顶点着色问题。本文的主要工作是设计了简单有效的可以应用于具有卫星厅的登机口分配的贪婪算法策略。
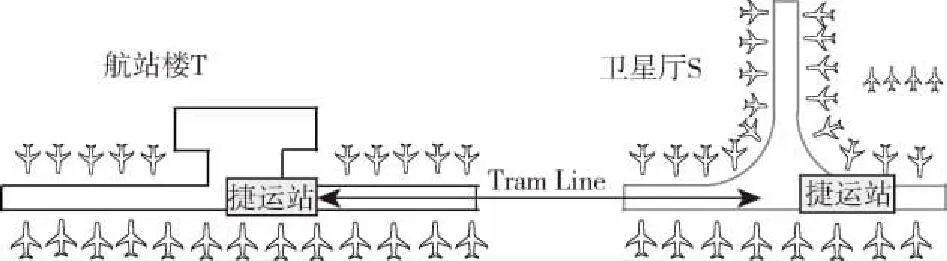
图1 卫星厅S相对于航站楼T示意图Fig.1 A sketch of satellite hall S relative to terminal building T
1 航班分配问题数学模型的建立
1.1 登机口分配的分析
根据登机口的规格,可将登机口分为国内-国内宽体机、国内-国际宽体机、国际-国内宽体机、国际-国际宽体机、国内-国内窄体机、国内-国际窄体机、国际-国内窄体机、国际-国际窄体机共8种类型。登机口分配是指根据航班的机型规格以及达到时刻、离开时刻,为每一个航班分配一个具体的登机口。在一天的不同时刻,由于到达的航班机型规格、航班数目、飞行类型(国际或者国内)不同,确定使用登机口的类型和时间也不同,具体分配登机口使用时,必须满足以下约束条件:
(1)对于每一个登机口而言,同一时间同一登机口只能分配给一个航班,或处于空闲状态。
(2)对于每一个航班而言,登机口是唯一的,即必须给每个航班分配一个且仅分配一个登机口。
(3)航班一旦开始使用某登机口,则该使用过程不能中断,直到使用完毕。
(4)登机口应与航班相匹配,即宽型航班只能使用宽型登机口,窄型航班只能使用窄型登机口。
对飞机进行登机口分配时,根据已知的航班时刻表,并且按照“先到先服务”的原则对航班进行登机口分配,这样就可以应用有序的顶点着色理论建立有关登机口分配的数学模型。
1.2 数据处理
以下为数据处理的具体步骤:
(1)根据飞机型号判断并保存所有航班的宽、窄类型。
(2)对所有航班根据到达类型和出发类型合在一起保存,并结合(1)中的宽窄将航班分为国内-国内宽体机、国内-国际宽体机、国际-国内宽体机、国际-国际宽体机、国内-国内窄体机、国内-国际窄体机、国际-国内窄体机、国际-国际窄体机共8种类型。
(3)将2018年1月19日0点作为起点,计算并绘制19日-22日不同时刻(单位:min )航班的数量,见图2;同时考虑间隔45 min后,计算并绘制19日-22日不同时刻航班的数量,见图3.
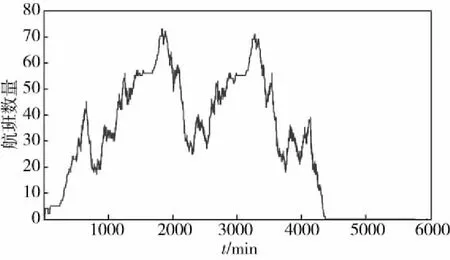
图2 19-22日不同时刻航班的数量 Fig.2 Number of flights at different time from 19 to 22
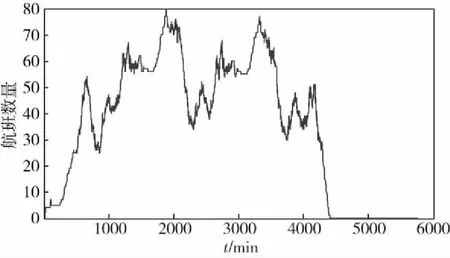
图3 考虑空档间隔后,19-22日不同时刻航班的数量Fig.3 Number of flights at different time from 19 to 22 after considering gap intervals
由图3可得:航班数最多为80个,而该机场可供使用的登机口共有69个,因此现有登机口无法安排下所有的航班,这就需要尽可能多的安排航班到合适的登机口,使登机口最大化被利用。
(4)将20日作为起点,由于航班到达时间和出发时间之差的最小值为50 min ,为处理简单,我们统一对19日到达20日出发的航班采用虚拟的到达时刻,即比出发时刻提前50 min,另外该到达时间不能超过起始时0点,如果位于0点之前,统一将0点作为虚拟的到达时间。
(5)同样,对于20日到达,而较长时间才离开的航班,将其到达时间延后50 min时间视为其虚拟的出发时间,若超过了24点,即已超过20日考虑范围,则可视为24点。
通过步骤(4)、(5)对24点和0点的特殊处理,可筛选并保存满足20日到达和20日出发的航班以及对应原顺序的下标。
(6)计算并绘制20日不同时刻的航班数以及考虑空档间隔45 min的不同时刻的航班数,见图4、图5.
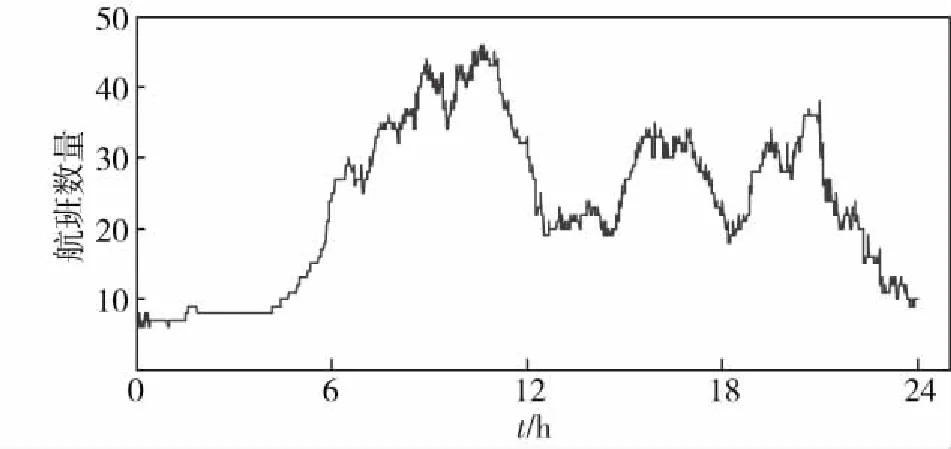
图4 20日不同时刻航班的数量Fig.4 Number of flights at different time on the 20th day
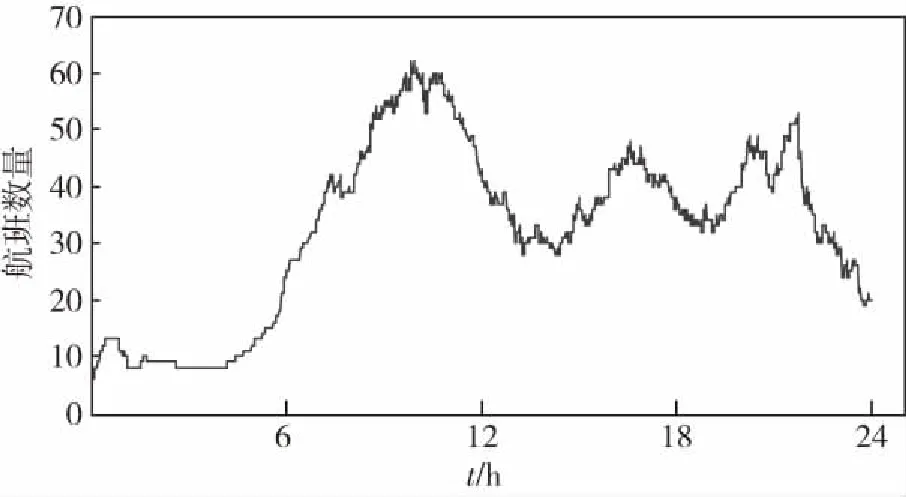
图5 考虑空档间隔后,20日不同时刻航班的数量Fig.5 Number of flights at different time on the 20th day after considering the gap intervals
(7)按照步骤(2)中的8种航班类型统计并绘制出20日不同时刻不同类型的航班数,以及考虑空档间隔45 min后20日不同时刻不同类型的航班数。图6、图7展示了国内-国内窄体机的结果,其他类型的航班数不在此一一展示。
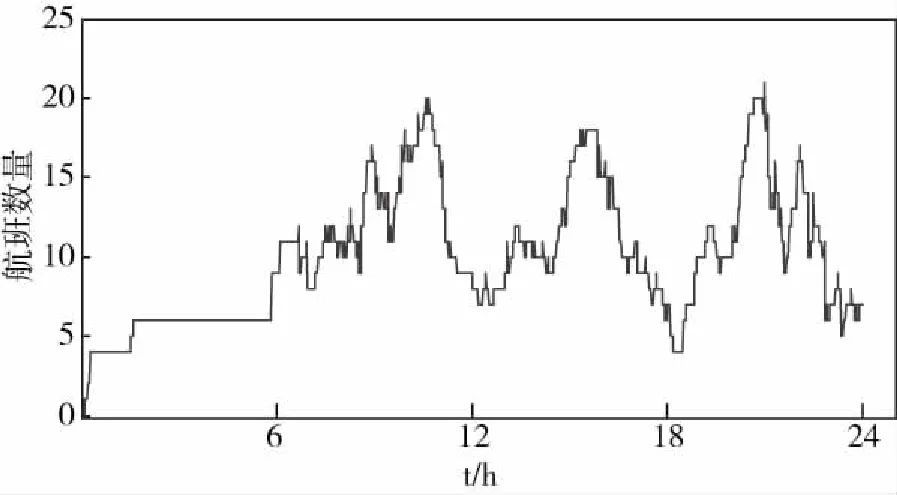
图6 20日窄体机国内-国内航班分布Fig.6 Domestic-domestic flight distribution of narrow body aircraft on the 20th day
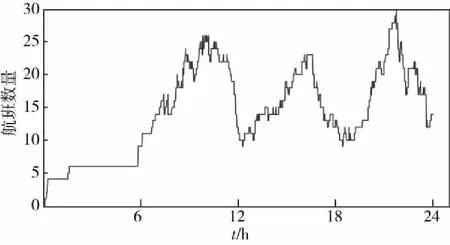
图7 考虑空档间隔45 min,20日窄体机国内-国内航班分布Fig.7 Considering the distribution of domestic-domestic flights on narrow-body aircraft with 45-minute gap on the 20th day
1.3 航班登机口分配的顶点着色模型
顶点着色问题在生产调度领域有着广泛的应用背景,已被应用于资源分配、货物存储和课表编排、频率分配[4-7]等问题当中。本文将航班-登机口分配问题看成顶点着色问题。首先引入航班登机口分配二元图G(V,R),对各航班按照到达时间的先后顺序依次编号,记为1,2,…,n,记V(G)={1,2,…,n},R为引入的邻接矩阵,用来表示各航班之间的关联情况,即R=(rij)n×n,其中:
rij=

当rij=0时表示航班i和航班j的时间不冲突,即可分配到同一登机口;当rij=1时表示航班i和航班j的时间相冲突,即不能分配到同一登机口。n表示航班数,题目中n=303.
接下来利用邻接矩阵,我们可构建航班-登机口分配优化模型为:
满足:
(1)[V1,V2,…,Vm+1]是顶点V的一个划分。
(2)航班的类型应与登机口的类型相匹配,并且登机口的数量满足一定的限制。
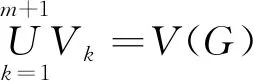
2 顶点着色模型的贪婪算法设计
2.1 与一般的顶点着色的不同
(1)按照“先到先服务”的原则,不同的航班根据到达时间构成一个自然的序关系。
(2)经典的贪婪算法中对于任意给定的所有顶点的一个全排列,一般用当前可用的最小色对当前的顶点着色。在该问题中,选择启发式规则是根据之前航班的起飞时间的先后顺序来选择登机口,选择已空闲时间最长的登机口,这样大大地增加了分配的鲁棒性,并且也有益于处理飞机不可避免的短时间的延误。
(3)经典的顶点着色问题,颜色的数目是没有限制的,而现在由于机场的条件,不同的颜色的数量有一定的限制。
(4)根据登机口的国内/国际、到达/出发、宽体机/窄体机等功能属性将其分为8类。
2.2 贪婪算法的设计
根据上述独有的特点设计贪婪算法求解,具体步骤为:
(1)寻找不同类型的登机口编号及个数,且根据其功能属性将其分成8种类型,即将颜色分为8类,根据航站楼的特点,每种类型的登机口由其数量限制,这样便获得颜色集和所允许的个数。
(2)计算邻接矩阵。
(3)利用贪婪算法求解。按落地时间“先到先服务”原则,依次为每个航班根据邻接矩阵找到能使用的登机口,并选择已空闲时间最长的登机口。若可供使用的登机口已经用完,则安排临时停靠方式。
2.3 实验结果与分析
所需安排航班总数为303个,所能提供的登机口总数为69个,通过上述算法可得到航班-登机口分配结果:宽体机安排比例为100%,窄体机安排比例为78.74%,共安排了249个班次的航班,航站楼T和卫星厅S被使用登机口的平均使用率(登机口占用时间比率)分别见图8和图9.
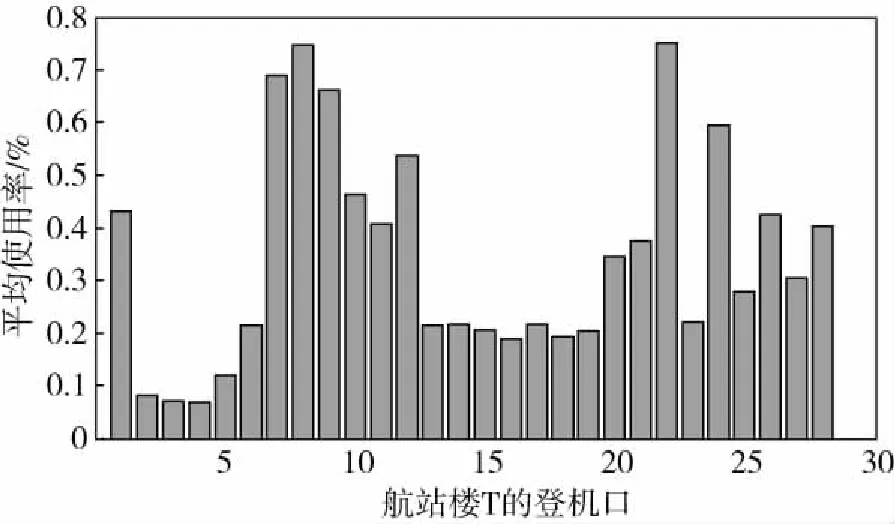
图8 航站楼T的每个登机口的平均使用率 Fig.8 Average utilization at each gate of terminal T
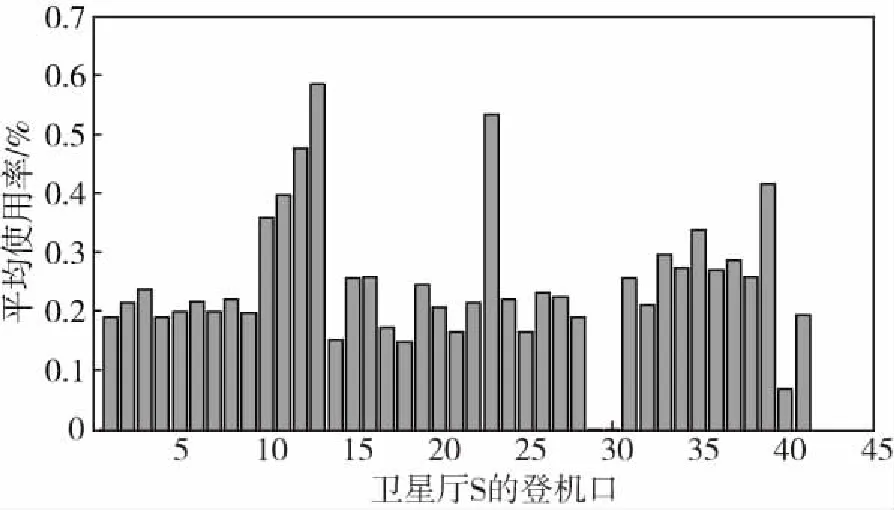
图9 卫星厅S的每个登机口平均使用率Fig.9 Average utilization at each boarding gate of satellite hall S
3 改进的顶点着色模型的贪婪算法设计
3.1 基于顶点着色方法的改进
根据有些登机口可以为多种类型(国际、国内)的航班服务的特点,根据宽、窄机,落地和起飞航班为国内或国际,将登机口可供使用的类型数分成三类,即仅供一类使用的,仅供两类使用的,供四类使用的。 从而将这些登机口(颜色)进一步分成8×3=24类,先考虑仅供一种类型航班使用的登机口,然后考虑可供两种类型航班使用的登机口,最后考虑可供四种类型使用的登机口。
3.2 改进的贪婪算法的设计
根据上述改进的顶点着色方法设计贪婪算法求解,具体步骤为:
(1)寻找不同类型的登机口编号及个数,分成8种类型,每种类型又分为3类,即只供该类型使用,可供两种类型使用,可供四种类型使用。
(2)计算邻接矩阵。
(3)利用贪婪算法求解。按落地时间“先到先服务”原则,依次为每个航班根据邻接矩阵找到能使用的登机口。在这些登机口中,优先使用只供该类型使用的登机口(颜色),然后使用可供两种类型使用的登机口,最后使用可供四种类型使用的登机口,并选择已空闲时间最长的登机口。若可供使用的登机口已经用完,则安排临时停靠方式。
3.3 实验结果与分析
通过上述算法可得到航班-登机口分配结果:宽体机安排比例为100%,窄体机安排比例为80.71%,共安排了254个班次的航班,航站楼T和卫星厅S被使用登机口的平均使用率(登机口占用时间比率)分别见图10和图11.改进的算法安排的航班数比2.2的算法安排的航班数多5个,说明改进的顶点着色模型的贪婪算法大大地提高了登机口的使用效率。
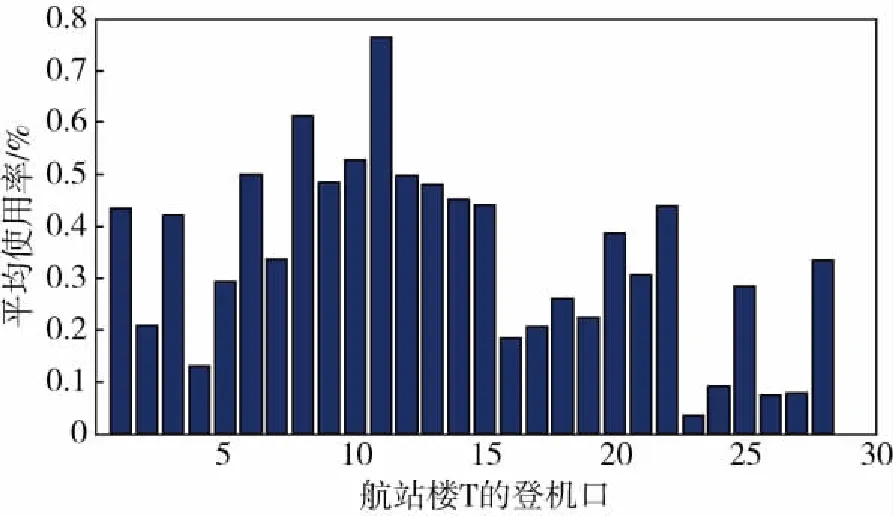
图10 航站楼T的每个登机口的平均使用率Fig.10 Average utilization at each gate of terminal T
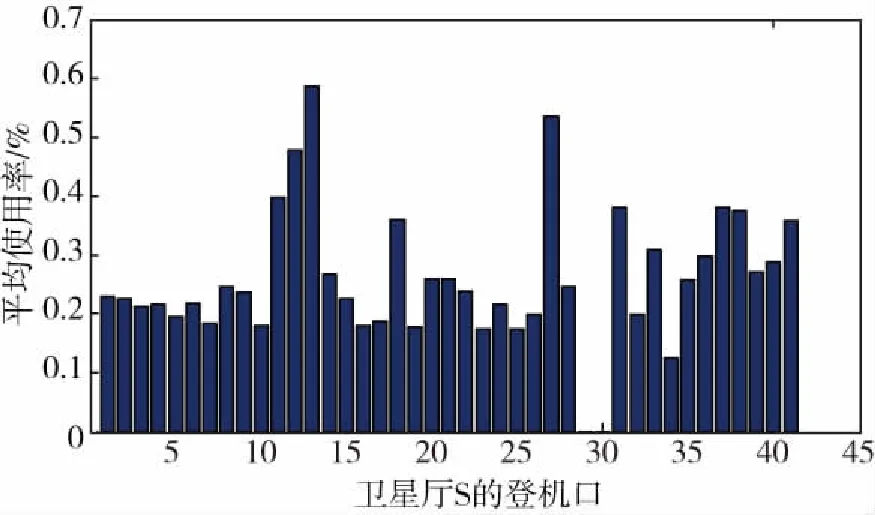
图11 卫星厅S的每个登机口平均使用率Fig.11 Average utilization at each boarding gate of satellite hall S
4 总结
本文提出了可以应用于具有卫星厅的登机口分配的贪婪算法策略。首先按照“先到先服务”的原则,运用简单的(选择已空闲时间最长的登机口)启发式规则为当前航班选择登机口,结果共安排了249个航班。然后我们进一步提出简单有效的启发式规则,即先使用仅供一种类型航班使用的登机口,然后考虑可供两种类型航班使用的登机口,最后使用可供四种类型使用的登机口,结果共安排了254个航班,大大提高了登机口的使用效率。所提出的算法简单有效,可操作性强。
