考虑中转旅客的登机口分配问题
2019-02-27任祎程上海理工大学管理学院上海200093
任祎程,韩 印 (上海理工大学 管理学院,上海 200093)
0 引言
机场登机口分配是空中交通管理(ATM)中机场运行的一项关键活动和静态预计划策略[1]。作为一个典型的航空公司枢纽,每天通常要处理数百个国内和国际航班,不合理的分配计划可能导致航班延误,客户满意度低,登机口飞机冲突拥堵和安全隐患,特别是机场容量现状以接近饱和的枢纽[2]。
登机口的分配通常考虑两个主要目标:最小化总航班延误和最小化登机口使用数量[3-4]。与登机口相关的约束条件,例如登机口只能容纳特定类型的飞机、两个大型飞机不能同时被分配到两个登机口,这些条件在登机口分配过程中必须得到满足[5-6]。当涉及的飞机数量较少时,登机口可以通过变换不同的目标条件,有效地生成登机口分配计划。但随着涉及的飞机数量的增加,可能的组合数量显著增加,很难有效地生成登机口分配方案[7]。
在文献中,登机口分配问题已被广泛讨论,并提出了相应的方法建议。这些方法可以分为两组:(1)基于人工计算的方法;(2)基于数学程序设计的方法。在早期,优化理论和计算硬件都非常有限,人工分配在解决登机口重分配问题被更广泛的应用[8]。C Zhang,D Lau等人(1997)提出了处理登机口分配问题的专家系统[9]。李耐毅提出了一个基于知识的顾问来帮助登机口分配决策[10]。陈鹏超开发了一种遗传算法来解决因航班延误而导致的登机口分配问题[11]。
随着优化理论和计算机技术的发展,利用数学规划技术优化求解登机口分配问题是可行的。因此,近年来提出了几种基于数学规划的方法[10]。王志清等考虑了机场临时关闭后的登机口分配问题,考虑分配飞机到一个备选的登机口,但是延误被忽略了[12]。杨越等人考虑了航班延误的选择,并提出了另一种实用算法来解决登机口分配问题[13]。刘君强进一步扩展了前人的模型,提出了一种考虑随机航班延误的登机口分配模型[14]。高菁等人提出了一个更实用基于规则的分配模型,建立了分别处理确定性航班和随机航班的模型[15]。薛清文等人在他们的登机口分配模型中考虑了中转乘客[16]。然而,他们的研究有两个局限性。首先,它只考虑最小化乘客的中转距离;其次,提出了二次模型,但没有给出求解该模型的算法。目前单纯的航班—登机口的优化分配问题已经被很好的解决。因此,如何给出合理的学科评价体系或模型来优化分配登机口,一直是机场建设研究的热点问题[17]。
1 问题描述
在建立数学模型之前,本文首先分析了登机口分配问题的特征:
(1)飞机进港时间和回退时间:飞机进港时间定义为飞机第一次到达登机口的时间,飞机回退时间定义为飞机从登机口后退的时间。图1中的示例演示了飞机的登机口到达和回退时间;

图1 飞机到达和起飞时间说明
(2)功能属性:每个登机口的国内/国际、到达/出发、宽体机/窄体机等功能属性事先给定,不能改变。
(3)临时机位:临时机位定义为位于停车区的虚拟登机口。
(4)中转旅客:从到达航班换乘到由同一架或不同架飞机执行的出发航班的旅客。
(5)转场限定:每架飞机转场的到达和出发两个航班必须分配在同一登机口进行,其间不能挪移别处。
(6)登机口限定:在每个时间点,登机口最多只能被一架飞机占用。
(7)属性匹配限定:飞机转场计划里的航班只能分配到与之属性相吻合的登机口。
(8)空挡间隔限定:分配在同一登机口的两飞机之间的空挡间隔必须大于最小空档时间。
(9)中转乘客:中转乘客的一次中转被定义为一对到达和离开航班。
2 航班—登机口模型建立
2.1 模型参数
为了便于介绍模型,后文要使用的主要模型参数符号如表1所示。
2.2 航班—登机口模型
决策变量:
TSi,表示转场飞机i停靠的登机口编号。
目标函数:
约束条件:
空挡间隔限定:GTAk,j+1-GTSk,j+1≥45min,k=1,…,K-1,j=1,…,J-1
属性匹配限定:
出发类型:yki·PSi=yki·GSkoryki·GSk=3,k=1,…,K-1,i=1,…,I
到达类型:yki·PAi=yki·GAkoryki·GAk=3,k=1,…,K-1,i=1,…,I
服务机型:yki·Ei=yki·Bk,k=1,…,K-1,i=1,…,I
转场限定
由于受实际情况限定:1≤TSi≤K,i=1,…,I
参数计算:
飞机i与登机口k的分配参数
登机口k第j个转机航班的到达时间:
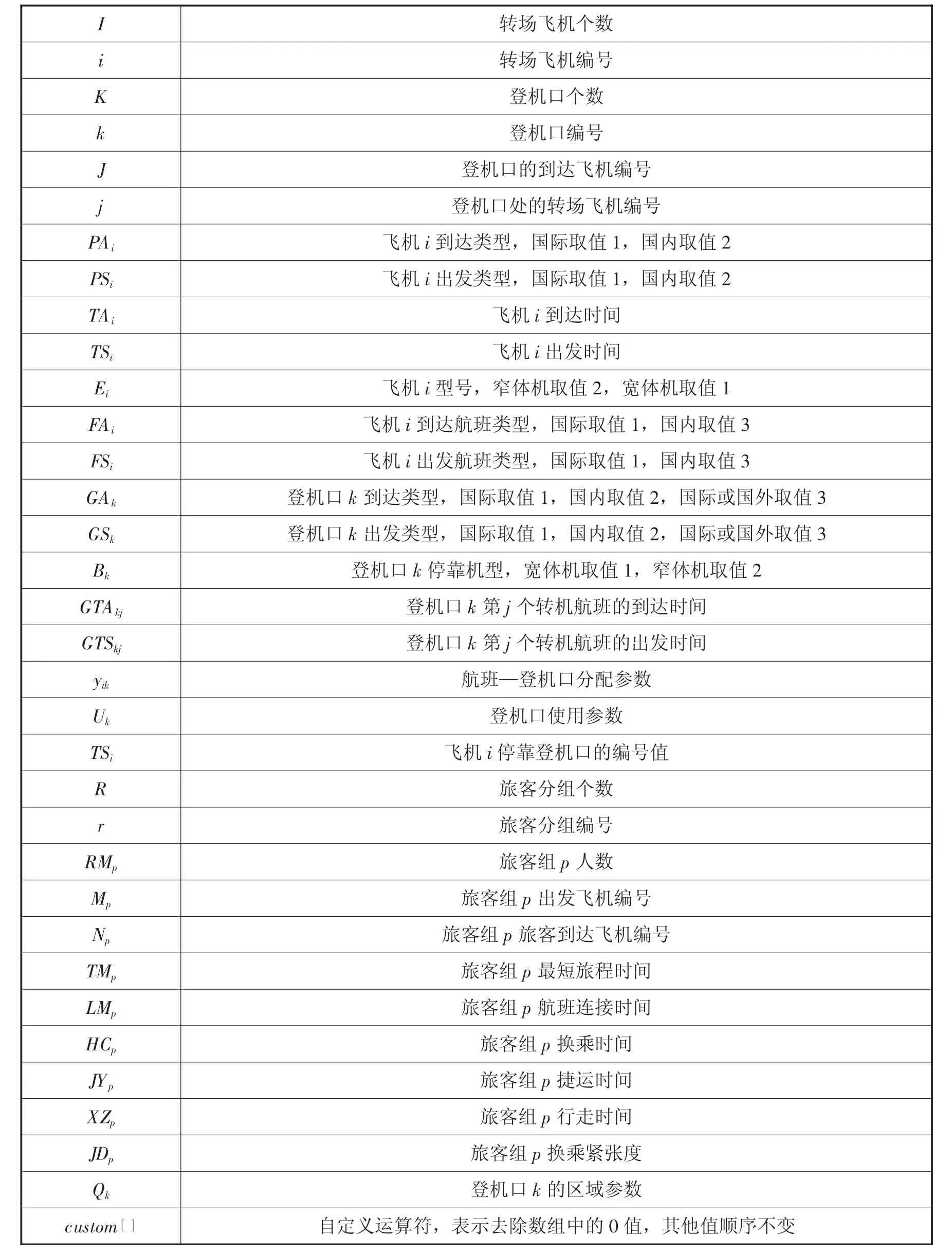
表1 符号和参数
登机口k第j个转机航班的出发时间:GTSkj=custom[yik,TSi],k=1,…,K-1
此处,custom[]为自定义运算符,表示去除数组中的0值,其他值顺序不变。
2.3 模型求解
从参考文献中可以看出,路径分配问题通常采用精确算法[18]和启发式算法[19]来寻找最优的解决方案。由于之前的大部分研究使用元启发式方法解决航班—登机口分配问题[20-21]。我们使用NSGA-II遗传算法来解决这个问题,并将空档时间约束添加到登机口的分配问题。
2.3.1 算法分析
为改善遗传算法在局部搜索能力方面的不足,提出将分支定界法与遗传算法相结合,构造了一种内嵌分支定界寻优搜索的遗传算法,在保证算法全局搜索能力的前提下提升局部精确搜索能力。对于遗传算法,为了适应算法结构提出了一种基于任务绝对顺序的编码策略:
步骤1:所有的飞机都是按照初始登机口到达时间升序排列的。
步骤2:求解航班—登机口模型的约束。最优解为每一个个体适应度函数的分数值。
步骤3:每架飞机都固定在一个登机口群上。
步骤4:在每次迭代中,会有数量有限的飞机固定在临时机位上。
步骤5:在前面步骤中违反临时机位的飞机数量的飞机—登机口组合被删除。
2.3.2 NSGA-II遗传算法
A.染色体编码和初始化
使用一个整数字符串来表示染色体是飞机与登机口的分配关系。
B.适应度函数
将目标表函数设置为适应度函数,并以此来评价群体中个体好坏。其中,目标最小化临时机位飞机数与最小化登机口使用数的适应度权重比,取500∶1。
C.遗传操作
(a)选择:采用游戏算法选择算子,使适应度好的染色体有更高的机会被选中。
(b)交叉:交叉是作用于两条染色体上,在一段时间内通过将两者结合起来产生后代染色体的功能。多数采用单点法交叉。
(c)突变:随机选择两个基因从染色体上,它们的值被交换并获得一个等级较弱的染色体。
3 算例分析
3.1 算例数据
由于旅行业的快速发展,航空公司机场现有的航站楼T的旅客流量已达饱和状态,为了应对未来的发展,现正增设卫星厅S。该机场航站楼T有28个登机口,卫星厅S有41个登机口。T和S之间有捷运线相通,假定旅客无需等待,随时可以发车,捷运单程一次需要8分钟。分配在同一登机口的两飞机之间的空挡间隔必须大于等于45分钟。待分配的飞机数为262架。
3.2 结果分析
通过优化处理计算得到最多可安排的航班数为222架,其中宽体机有42架,窄体机有180架,成功分配到登机口的宽体机和窄体机的航班数量对比如图2所示。
观察图3的饼状图发现1-1(国内到达—国内出发)的机型不再全部为窄体机,有一小部分为宽体机。
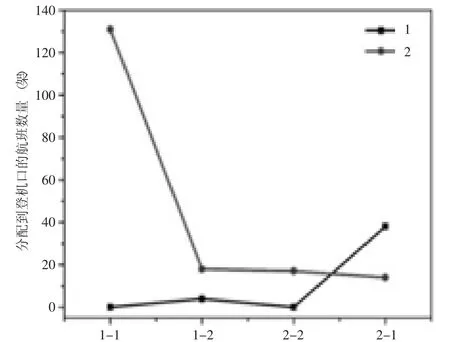
图2 成功分配航班数量(宽体机和窄体机)

图3 成功分配航班比例
航站楼(T)和卫星厅(S)登机口的最少使用数目,结果如图4所示,发现至少使用64个登机口才可以最多的安排航班222架。
图5给出了航站楼(T)和卫星厅(S)的被使用登机口的平均使用率(定义“平均使用率”为登机口的占用时间比率),发现大多数的登机口的平均使用率都远远大于50%,其中使用率在70%~100%间的登机口占大多数,即登机口的使用率符合实际情况。
表2为航班—登机口分配结果汇总和有关属性的标注。成功分配飞机数为222架,停在临时机场的飞机有40架,使用的登机口数量为64个。
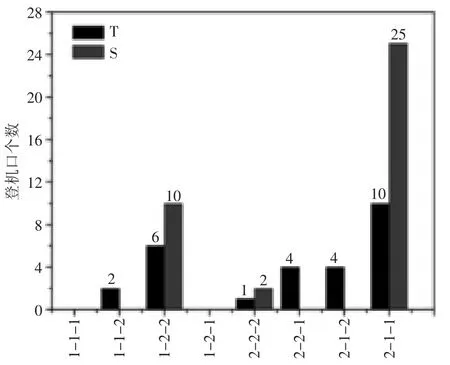
图4 T和S登机口使用数目
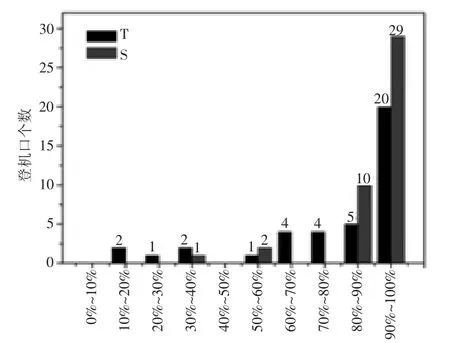
图5 T和S登机口的平均使用率
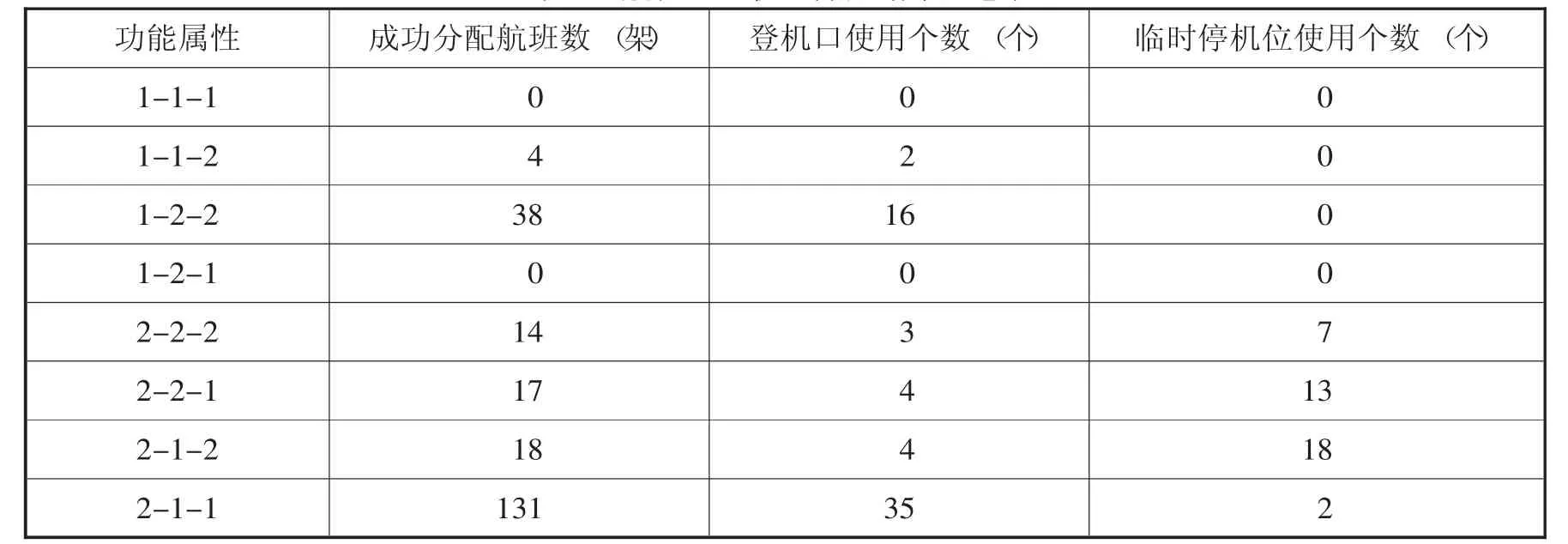
表2 航班—登机口分配结果汇总表
如图6所示,换乘时间在30~35分钟以内的中转旅客比率最大为27%,在5分钟以内的中转旅客最少为0。
如图7所示,紧张度在0.1~0.2的中转旅客比率最小为0,紧张度在0.6~0.7的中转旅客比率最大为28%。
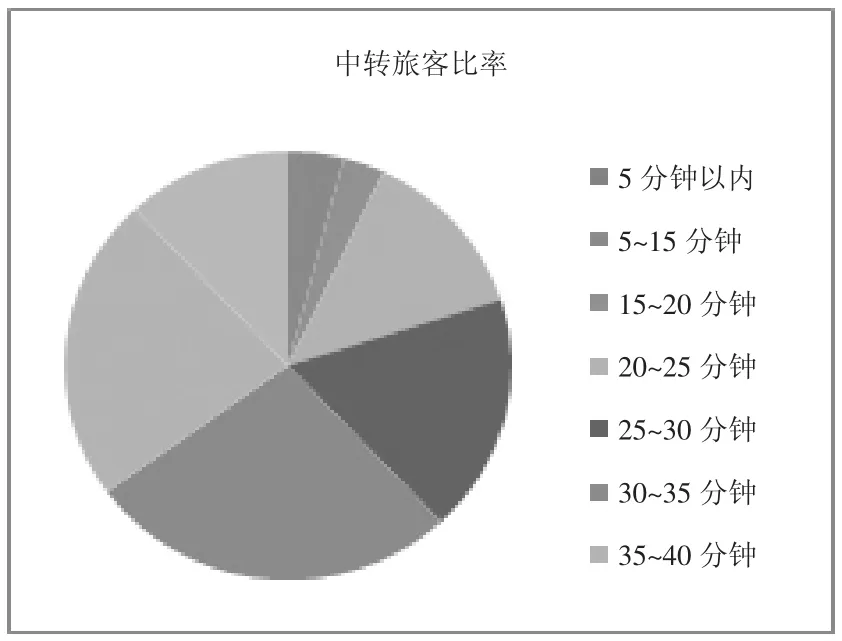
图6 中转旅客在各个时间段的比率
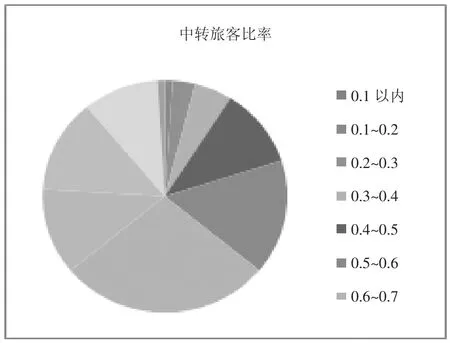
图7 中转旅客在各个时间段的比率
4 结束语
本文针对机场航班登机口分配问题,根据转场限定、登机口限定、属性匹配限定、空挡间隔限定,建立飞机—登机口分配的一个二次0~1整数规划模型。采用改进的NSGA-II遗传算法,并利用MATLAB对模型进行了求解。通过对一个算例分析,验证了本文方法的可行性和有效性,为管理者更好地进行航班登机口的分配提供了指导意见。
