中职数学与建筑工程测量“专基融合”并行教学的实践研究

【摘 要】本文通过分析中职数学教学与专业应用剥离的原因，尝试从中职数学和建筑工程测量两门课程的教学计划整合、联合备课、选修课程校本教材的开发以及教研探索等方面进行实践研究，寻求两门课程相关教学内容的齐头并进、相互促进，最终实现基础课程和专业课程的教学融合。

【关键词】专基融合;并行教学;中职数学

教育部发布的《中等职业学校数学课程标准（征求意见稿）》明确指出：数学课程教学要“体现职教特色，注重实践应用”。新课标建议在教学实施中加强数学教学内容与专业课程、社会生活、职业应用的联系，设计合适的教学情境，引导学生通过分析建立合适的数学模型，并借助数学工具解决问题，促进学生实践和应用能力的提升[1]。

1   中职数学知识在专业应用中的问题

中职学生在面对专业实际问题时，往往束手无策。

如建筑工程测量课中有一题，图1所示ABCD为建筑红线，在AB间有已建建筑物影响通视。为测量AB间距并定出AB方向，现在D点测得∠BDA=49.5°，DB=102.9m，DA=67.1m。

（1）计算AB边长。

（2）求∠DBA、∠ABD大小。

对于此题，笔者教授的两个班级整体上的解题正确率均不高。而学生基本都会做数学教材上与本题相近似的两个小题，具体题目如下。

（1）在△ABC中，已知∠A=30°，，，

（2）在△ABC中，已知AB=3，BC=4，AC=，求∠B。

以上情境引发了笔者思考：学生对题目所涉及知识点的掌握还是不错的，但学生在应用相关知识解决类似的专业问题时，预期目标的达成并不理想。为什么解类似的题型，学生的表现会截然不同呢？以上问题困扰着笔者，促使笔者在教学过程中不断关注学生的应用能力，分析和改进教学策略。

2   问题产生的原因分析

2.1  数学课与专业课教学的割裂

基础课教师和专业课教师各自为政，缺少必要的沟通。多数教师把教学重点放在完成本课程的授课任务上，只简单介绍或者直接忽略讲解相关应用或知识的来源[2]。

2.2  学生创新思维的匮乏

固有的学习模式让学生产生惯性思维，如测量的题目就得用测量课所学的知识解决。学生缺少创新意识和创新思维，在数学课上看到一个所谓的“专业”题，就不知道该怎么做了。

2.3  数学教材与专业应用缺少衔接

中职数学中的三角函数、向量、立体几何等章节均与建筑相关知识密切相关，但是教材中应用案例几乎没有。同时，数学课教材的编排没有考虑到与专业课程应用的并行或协同，造成学生专业课上要应用的数学知识数学教师还未教或者学过太久已淡忘[3]。

3   “专基融合”并行教学的实践探索

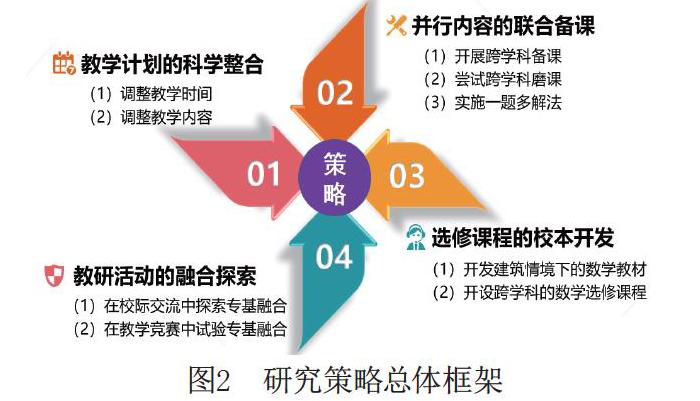
根据教学需求和学生现状的调查，对比分析数学课“三角函数”一章与测量课的关联内容（如图2），笔者开展了一学年的教学研究和实践探索。

3.1  教学计划的科学整合

基础课教师和专业课教师互读对方课程的教学课本，对彼此的课程有初步的认识之后，再开展教研组间的联合教研活动，对照数学课和建筑工程测量课可结合的知识点，一起制定两门课的教学计划[4]。

3.1.1  调整教学时间

调整教学时间，合理安排教学内容。如在专业课中应用某数学知识点前，完成相应的数学知识教授，为专业课做好基础知识储备;或是在数学课授课前，通过专业课程实践积累一定的应用案例，为数学课提供丰富的教学素材和建立相关专业情境。当然，在调整进度的同时也要注意维护课程总体的知识体系和进度不混乱。

3.1.2  调整教学内容

梳理测量课各章节内容对数学知识的要求。通过通读测量课本和认真对照分析，与专业教师共同研讨，归纳、整理所需的数学知识，合理重构数学教学内容。如专业课中水平角的测量，需学生掌握度分、秒的加减，而现阶段数学教材中并没有这部分内容，所以可以加以补充;专业课中方位角的计算需用到象限角的内容，那么可适当增加课时，为学生专业课的学习打好基础。

3.2  并行内容的联合备课

3.2.1  开展跨学科备课

跨学科备课首先要组织跨学科的教研活动，广泛听取教研组骨干教师对教学改革的意见、专业课和基础课教师的教学需求。其次要结合实际，对后续如何联合备课、如何协同组织教学进行思考和规划[5]。如针对“余弦定理的应用”这一内容，可选用测量课中的案例作为数学新课的引入和课后的拓展。新课引入时，若是数学教师能抛出一个专业课的问题，激发学生的学习兴趣和内在需求，那么学生自然更乐于深入探索新课内容。

3.2.2  尝试跨学科磨课

跨学科教学是新的挑战，在完成教学设计后，要及时安排说课活动，通过邀请两个教研组骨干教师现场观摩、研讨，对说课中暴露出来的问题进行处理，对教学设计进行调整和完善。然后组织公开课，安排专业课教师和数学教师共同听课。在课后组织评课，并观察和研究学生在课上的反应，之后再次调整、完善教学设计。

3.2.3  实施一题多解法

一些知识内容在专业课和数学课上虽然原理相通，但表现形式不同。如对于一些題目，专业课中有专业的公式和解法，但用数学公式也能求出相同的结果。可以对这样的题目进行整理，与专业教师协商开展“互助教学”，在数学课上“提一提”专业解法，在测量课上也“说一说”数学解法，从而实现跨学科的“一题多解法”，拓展学生的思维。

3.3  选修课程的校本开发

3.3.1  开发数学校本教材

现阶段缺少建筑专业与数学课程相互渗透的中职数学教材，所以编订一本校本教材很有必要。建议给测量等专业课程设置固定的数学合作教师，这样更有利于加深数学教师对专业课程的理解，从而在实践中开发和完善与专业相结合的数学校本教材。

3.3.2  开设跨学科的数学选修课程

开发与专业知识结合的应用数学选修课，形成具有专业特色的数学教学内容。在数学必修课程中，受课时等因素限制，无法完全跟学生讲清楚的部分，可放到选修课中讲。条件允许的情况下，甚至可以尝试数学教师和专业教师各自负责一部分内容，“同台”授课的方式。

3.4  教研活动的融合探索

3.4.1  在校际交流中探讨“专基融合”

各中职学校师资参差不齐，且很多基础课教师只把精力放在日常教学中，对于知识结构的完善、教学能力的提升不太重视。因此，基础课教师应积极参加各种培训，有选择性地到一些优秀的兄弟学校进行观摩和交流，在校际交流中学习和探讨专基融合。

3.4.2  在教学竞赛中试验“专基融合”

参加各类教学竞赛，不失为一种检验课程设计“优劣”的方法，同时来自各校的优秀教师可以相互学习、切磋、取长补短。另外，各行业专家的点评和指导也能为教学提供新的视角。

4   教学改革的初步成效

4.1  数学与工程测量的教学衔接更紧密

“专基融合”的教學模式下，数学课与专业课的内容得到了有效整合。数学课为专业课提供了必要的基础理论支持，专业课也为数学课提供了生动的专业背景和案例，两学科的教学衔接更紧密。

4.2  专业情境下的数学课堂更有吸引力

以专业课为背景的案例情境吸引了大部分学生的注意力，与原本枯燥的“裸数学”课堂相比，这样的课堂更接地气，并且更具有实用性。

4.3  学生的数学应用能力得到有效提高

“专基融合”的教学模式，使学生对数学的认识不再停留在理论层面。在专业上、在生活中“用数学”的观念已逐渐深入人心，并真正得到实践。有效提升了学生的数学应用能力，也促进了学生创新思维的发展。

【参考文献】

[1]教育部职业教育与成人教育司.中等职业学校数学课程标准（征求意见稿）[Z].2018.

[2]侯欣诲.中等职业学校数学课与专业课整合的实践研究——以汽车维修专业为例[D].上海：华东师范大学，2010.

[3]叶环.机械专业中重构中职数学教学内容的实践研究[D].长春：东北师范大学，2012.

[4]王丹红.中职数学教学为专业课服务的现状调查研究——以郑敬诒职业技术学校为例[D].贵阳：贵州师范大学，2014.

[5]黄佳宁.中职数学教师学科知识水平现状调查研究——以《三角函数》学科知识为例[D].福州：福建师范大学，2018.

【作者简介】

姜丽芸（1983～），女，汉族，浙江嘉兴人，本科，中专讲师。研究方向：数学教学。