基于激光移频回馈技术远距离振动测量研究

（江苏大学 机械学院，江苏 镇江 212013）

引言

远距离微弱振动信号探测在机械制造、国防和军事等领域具有非常重要的意义[1-2]。近年来，随着激光测量技术不断进步和发展，远距离振动测量技术也取得了一系列新的研究成果。国外ZHU Zhigang 等人利用激光多普勒振动（LDV）仪实现了100 m 外物体振动测量，使用反光带可以实现300 m的测量距离[3]。国内吕韬等人搭建了全光纤激光相干测振系统，重建出150 m 外矿泉水瓶的振动信号，可以将其当做声传感器，重构语音信号[4-6]，但该系统未考虑对表面反射率较低物体振动测量。此外由于使用窄线宽激光器易受温度影响引起相位噪声，继而影响系统测量精度，限制了应用发展。汪啸等人采用反射式调制技术研制了收发独立的激光测振系统，实现200 m 处物体振动测量[7]。但该方法仅考虑玻璃物体探测，采用收发分离系统会受到探测区域的限制，在实际使用中寻找接收光斑不易，同时激光器功率较高（2 W）。总之，目前技术很难实现在低功率激光器下远距离非合作目标振动测量。

激光回馈技术是一种高灵敏探测手段，可以弥补以上不足。1963年P.G.R.King 等人首次提出了激光回馈干涉理论[8]。近年来，激光回馈技术受到了广泛关注与研究[9]。激光回馈现象是指在激光应用系统中，激光器输出光被外部物体反射或散射后，以相同光路返回到激光器谐振腔内，并与腔内光场干涉，从而调制激光器输出功率。通过分析激光强度、偏振态、工作频率和相位等特性变化，可以解调出外腔物体运动信息。因输出信号特点与传统双光束干涉信号相似，也称为自混合干涉。激光移频回馈技术是在外腔中插入移频器件，回馈光频率发生变化。移频光回馈下，系统具有一定增益，且移频频率与弛豫振荡频率越接近，增益因子越大，从而提高系统测量灵敏度。激光移频回馈干涉技术具有灵敏度高、结构简单、易准直等优点，被广泛应用于位移测量[10-11]、速度测量[12-13]和材料热膨胀系数（TEC）测定[14]等领域。激光回馈技术也曾应用于振动测量[15-17]。Otsuka 等人利用LiNdP4O12（LNP）微片激光器搭建了激光自混合测振仪，并且通过单模光纤成功实现2.5 km 外物体振动信号的探测[16]。吴鹏等构建了激光回馈振动测量系统，实现了25 m 外振动信号探测[17]。激光移频回馈技术对弱回馈光具有非常高的灵敏度，因此对远程非合作目标振动测量有突出优势。

文中基于固体微片激光器移频回馈，构建远距离振动测量系统，在保证精度的前提下进一步提高系统工作距离与入射角度范围，通过仿真验证测量方案的有效性。实验中利用硬纸盒作为测量目标，利用单频信号进行激励，可实现入射角度为±60°下100 m 外振动波形清晰获取，并且信噪比仍接近20 dB。此外，系统也支持对多种非合作目标振动，进一步提高了系统实际应用的灵活性。

1 实验系统

出射照射在物体时产生背向散射，回馈光沿原路返回到激光器内并与腔内光场发生干涉。当物体振动时，回馈光的相位变化引起干涉信号变化。通过解调相位的变化得到物体的运动信息，远距离振动测量系统的结构组成如图1所示。

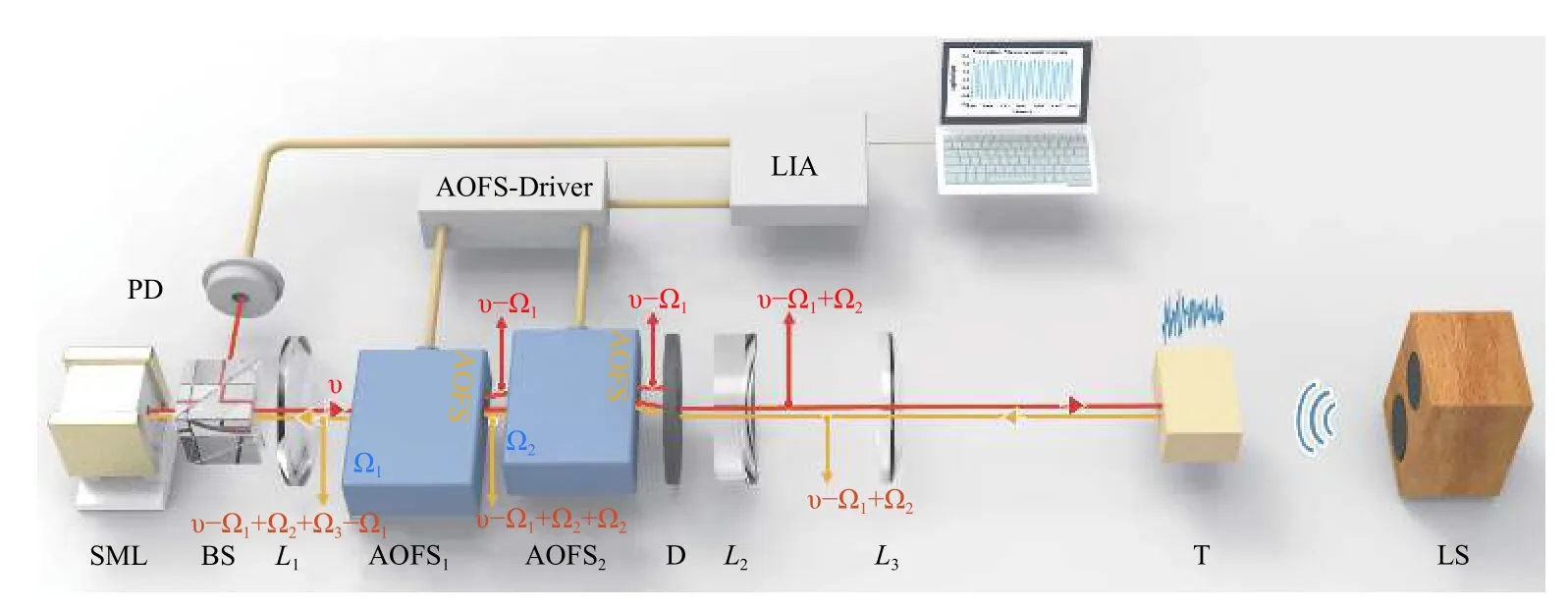
图1 实验装置示意图Fig.1 Schematic of experimental device

1.1 光路结构

图1中，SML（solid-state microchip laser）为固体微片激光器，其微片材料为Nd：YVO4。微片由半导体激光器（LD）进行泵浦产生1064 nm 激光，并工作在单纵模状态。分束器（BS）将出射光分成两束。反射光被光电探测器（PD）接收并转化为电信号，透射光经过准直透镜L1，并被一对声光移频器（AOFS）调制。由于声光移频器的工作频率通常较高，因此使用两个AOFS 进行差动移频，移频量为Ω。若AOFS1和AOFS2工作频率分别为Ω1和Ω2，且出射初始光频率为υ，则透射光经过AOFS1产生−1 阶布拉格衍射，此时出射光的频率为υ−Ω1；再次通过AOFS2产生+1 阶布拉格衍射，出射光频率为υ−Ω1+Ω2，简写为υ+Ω，如图1中红色光束所示。光束经过透镜组准直后打在被测物体（T）上并发生散射，背向散射光再次通过AOFS2和AOFS1并发生衍射。因此，移频回馈光的频率为υ−Ω1+Ω2+Ω2−Ω1，简写为υ+2Ω，如图1中黄色光束所示。虽然固体激光器发散角仅为10 mrad，但当测量距离增加时，光束发散明显，激光的光功率密度也迅速降低，同时发散形成较大面积光斑会引入大量的环境噪声，降低测量的精度。因此，本文利用透镜L2和L3组成伽利略系统对激光束准直，增加回馈光功率密度，从而在长距离测量的情况下确保为激光回馈系统提供足够的信噪比。

1.2 信号解调

被物体散射光回到激光腔内，与腔内光场产生干涉。测量光路对输出功率引起调制ΔI可以表示为[18]

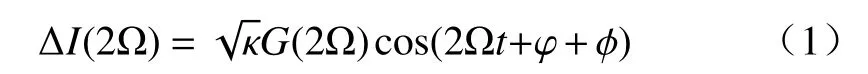
其中：ϕ为测量光路初始相位值；φ是与外腔长度有关相位；κ为系统有效回馈水平；G（2Ω）是与移频频率有关增益系数，可表示为[19]

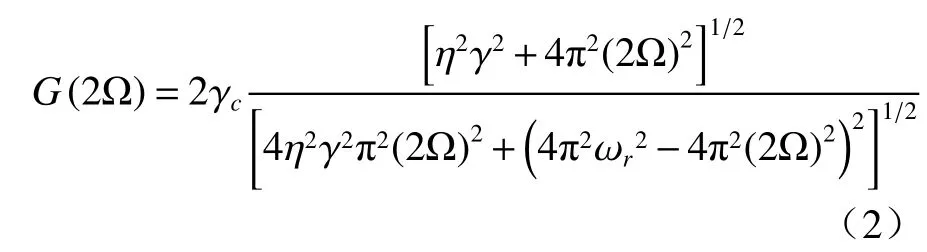
其中：γc为腔内光场衰减速率；η为激光器相对泵浦水平；γ为腔内反转粒子的衰减速率；ωr是弛豫振荡信号。当移频频率接近2Ω 接近弛豫振荡频率ωr时，回馈效应的增益系数G可以达到106。因此，激光移频回馈系统对微弱信号仍具有超高灵敏度。PD 检测到由回馈光调制的激光输出功率，并将其转换为电信号。利用锁相放大器（LIA）获取相位信号，通过采集和解调相相位的变化，可以得到外腔长度的相应变化为

其中：λ为激光波长；n0为空气折射率。假设物体产生受迫振动与声源振动一致，通过记录和分析外腔长度随时间变化，再进行谱分析得到物体振动频率与幅值。

2 工作距离与入射角度分析

光束传播过程如图2所示。

图2 光束传播示意图Fig.2 Schematic of beam propagation

激光出射后到达物体上光功率Pi为

式中：Po为激光发射功率；K为光学系统透过率，由系统中透镜组透过率与AOFS 衍射效率决定。

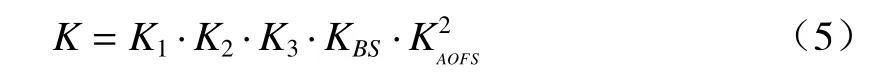
式中：K1、K2、K3为透镜L1、L2、L3透过率99.5%；K BS为分光镜透射率80%；K AOFS为声光移频器衍射效率60%。Tα为大气透过率[20]，在空气能见度为10 km时，Tα=e−0.33×L/1000；At和As分别为被测物体与光斑面积。假设光斑强度分布均匀，测量系统接收到回馈光功率为

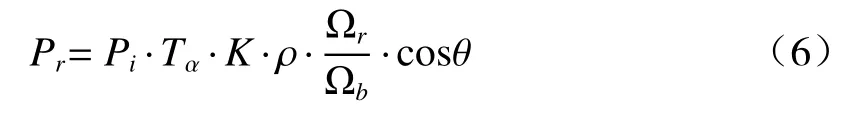
其中，θ为激光发射方向与目标T法线之间所夹锐角。对于理想散射体，其反射率ρ=1，后向散射立体角Ωb=π，系统入瞳角Ωr=Ar/L2。Ar=π·r02为系统接受口径面积，r0=6.2 mm为系统出射光斑半径，L为激光器外腔长度，可以看作激光器与被测物之间距离。光斑面积小于物体面积，因此At=As。结合（4）和（5）式，系统有效回馈水平κ为激光器接收光功率与输出光功率比，可表示为：

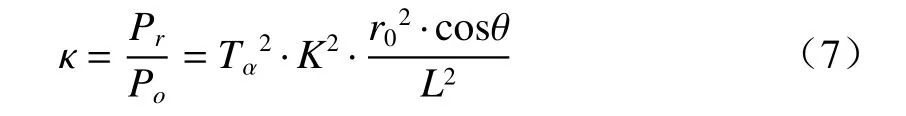
由（1）式得到，得益于增益系数G，系统有效回馈水平κ可低至10−12，系统最大工作距离可达103m。实际应用中，工作距离会小于理论结果，因此后续实验选择最大工作距离为100 m，对应系统有效回馈水平为2.82×10−10，并在此距离上选择最大入射角为±80°，对系统有效回馈水平为4.90×10−11，在回馈光强度上系统均可满足测量要求。根据（7）式可得系统在正入射时工作距离与系统有效回馈水平关系，以及工作距离为100 m时入射角度与系统有效回馈水平的关系，如图3所示。

图3 回馈水平与工作距离/入射角度关系Fig.3 Relationship between effective feedback level and working distance /incident angle

此外，从（7）式可得，提高接收孔径r0可实现工作距离L增加，本系统中接收孔径为12.4 mm，远小于一般LDV系统的100mm[4]。因此，在相同有效回馈水平下，通过增大接收孔径大小可以获得更长工作距离。

3 实验

实验装置实物如图4所示，由硬纸盒，音响和远距离振动测量系统组成，出射光正入射打在被测物体上，利用音响产生单音节信号驱动硬纸盒产生单频振动，扬声器与纸盒之间距离约为0.5 m，系统工作距离，即激光光束到振动物体距离为100 m，激光出射功率为10 mW。

图4 振动测量实验装置实物图Fig.4 Photo of vibration measurement system

图5所示为经过探测器光电转换以及示波器傅立叶变换之后光功率谱信号，其中ωr是弛豫振荡信号。测量信号在激光功率谱中引起2 Ω的调制峰，通过滤波提取以及外差解相方式可以得到测量光路的相位变化。得益于激光回馈效应的高增益特性，在系统工作距离高达100 m 情况下，测量信号的信噪比仍然达到25 dB 以上。

图5 正入射下光信号频谱图Fig.5 Optical signal spectrogram under normal incidence

实验中，扬声器播放声信号如图6所示，声音频率为500 Hz。

图6 500 Hz 扬声器激励信号波形和频谱图Fig.6 500 Hz loudspeaker excitation signal waveform and spectrogram

系统测量结果如图7所示，从图中可以得到，恢复信号有明显单一振动频率，且计算频率与原始信号频率基本一致。此外，恢复的波形存在低频噪声，这是由于在长距离探测时，空气扰动、温度以及环境噪声干扰使得恢复信号产生偏移，但从局部放大图中看出，物体振动信号依然清晰可辨。

通过在3个不同时间段里对200 Hz到1000 Hz、间隔100 Hz，以及2 000 Hz到10000 Hz、间隔1000 Hz的18个频率进行测量，得到测量结果的误差棒图如图8所示。横坐标为标准频率，纵坐标为测量频率与标准频率之差。从图中可以看出，随着频率增高，测量误差大体趋势在逐渐增大，这是由于频率越高产生声压越小，从而被测物体响应越弱，并且被测物体的振动响应特性也对测量结果有一定影响。实验测量结果误差均在0.1%，说明系统能够较为精确实现100 m 远的微弱振动信号探测。

图7 500 Hz 重构振动信号波形和频谱图Fig.7 500 Hz reconstruction vibration signal waveform and spectrogram

图8 频率测量误差棒图Fig.8 Frequency measurement error bar

4 系统性能测试

4.1 多入角度测试

在实际应用中，很难做到每次测量都能够以正入射的角度去探测，因此系统大入射角度决定了实际应用的灵活性。本实验通过改变被测目标表面法线与入射光束的夹角θ（如图2所示）来探究不同入射角度对振动系统探测的影响。系统工作距离为100 m，被测物为硬纸盒，图9（a）～图9（d）分别为入射角度为30°、45°、60°以及80°情况下的光信号频谱图。从图中可得到在入射角为30°时系统信噪比与正入射时基本相同，当入射角为60°时信噪比依然接近20 dB，当入射角为80°时信噪比降低至12 dB，系统回馈水平较低，实验结果与图3仿真基本一致。

图9 不同入射角度下光信号频谱图Fig.9 Optical signal spectrogram under different incidence angle

分别在上述不同入射角下测量500 Hz 振动信号，图10（a）～图10（f）分别对应入射角度为0°、30°、45°、60°以及80°情况下的测量结果。随着入射角度增加，振动的幅值在逐渐减小，这是因为系统只能探测沿光轴方向振动信号。当入射角度小于60°时，振动波形清晰可分辨，当入射角为80°时，恢复信号的波形渐失真，如图10（f）所示不能再重构原始信号。一方面由于系统回馈水平降低，另一方面沿光轴方向振动幅值太小导致信噪比不够。系统入射角的最大范围应保持在−60°到60°之间，并且在受环境噪声干扰较小的最优范围为−30°到30°之间。

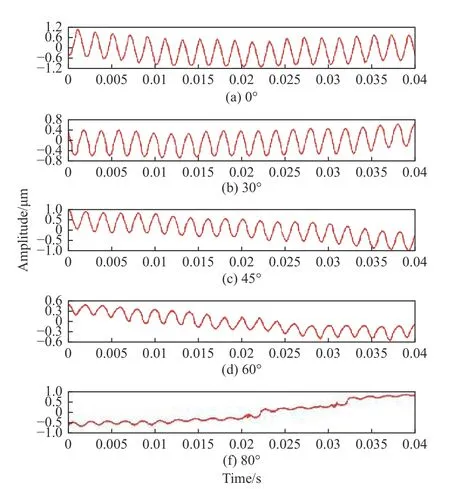
图10 不同入射角度下振动信号时域图Fig.10 Time-domain of vibration signal at different incident angles

4.2 非配合多目标测量

探究系统对多种非合作目标测量情况，使得更贴近实际应用，并进一步拓展系统应用场合。实验中分别使用了奶粉袋、泡沫以及海绵代替了硬纸盒进行测量，系统工作距离仍为100 m，声源频率为500 Hz，对应的时域波形如图11（a）～图11（d）所示。

从图中可以看出，激光回馈高灵敏特性使得系统在不同非合作目标测试下均能够获得清晰的波形。图11（d）中可以看出由于海绵材料吸音特性，使其在声压激励下难以振动，因此无法获得准确的波形，其他被测对象均可获得振动信号。此外，实验中对上述目标也进行了多角度实验，在入射角为−60°到60°下也均可重建振动波形，重建最优范围为−30°到30°。

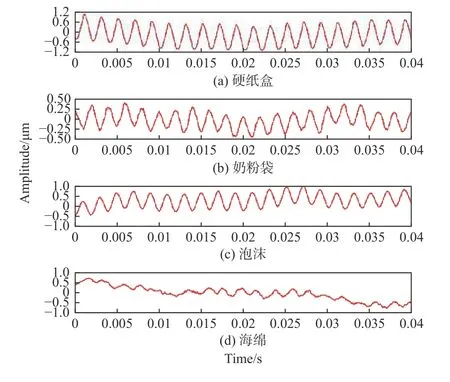
图11 不同物体下振动信号时域图Fig.11 Time-domain of vibration signal recovered with different targets

5 结论

通过研究与实验，所构建的基于激光移频回馈远距离振动测量系统，通过测量目标振动产生的位移获得振幅与频率，不仅可以实现100 m 距离内非合作目标振动信号精确探测，频率测量误差在0.1%内；同时支持高达±60°的入射角范围，具有20 dB 良好信噪比。此外，系统也支持对多种非合作目标振动测量，能够在实际测量中灵活方便地选取探测地点和目标物，提高了系统实际应用的灵活性。

我们未来将继续研究如何改善远距离振动测量系统的性能，例如使用聚焦光路和提高接受口径来提高接受散射信号的强度，进一步提高系统测量距离，以便满足远距离振动信号探测更高需求，在救灾和远程监视领域具有广阔应用前景。