基于数据挖掘的光纤通信网络异常数据检测研究
2020-04-12
(内蒙古农业大学 计算机与信息工程学院,内蒙古 呼和浩特 010018)
引言
随着计算机网络应用与光纤传感技术的不断发展,基于光纤传输的互联网络被大量应用于生活、生产等领域,由于光纤传感网络具有通信容量大、传输距离远、成本低等特点[1-2],所以得到了广泛推广及应用。随着光纤传输网络中用户端以指数量级增长,通信故障造成的异常数据也不断增多。在规模巨大的互联网数据中快速分析识别异常数据并加以定位是十分困难的,因为数据传输过程中不可能将所有信息全部获取后才完成分析及信息识别,所以必然有很多信息在传输过程中被省略,这些省略的信息中不可避免的存在有效信息,从而导致信息熵的增加,降低了现有通信故障检测效率[3]。
光纤通信网络[4]中异常数据的识别需要从当前所有数据中提取异常数据的数据特征及模式结构,将异常数据特征与模式结构作为训练样本进行学习,从而对大数据中其他故障终端产生的异常数据进行快速精确识别[5]。利用该算法找出异常数据所对应的各变量间的逻辑关系。光纤传感网络中数据量巨大,采用大数据挖掘技术能够更好地将异常数据特征提取出来。传统的识别方法主要包括:BP神经网络[6]、时序分析法[7]、遗传算法[8]、粗糙集[9]等。BP神经网络可适用于此类非线性问题并且具有一定的自学习能力,但在数据量很大时容易陷入局部极值问题[10];时序分析法是基于时间顺序对数据进行统计分析的方法,本质是统计规律的总结,它是网络中异常数据分析的常见方法,对具备先验知识的数据分类简单易实现,但预测精度较差[11];遗传算法可实现多个体同时比较,有利于多参数协调优化,其本质是参数权值的动态调整,这与网络数据交互是十分相似的,但其算子参数选择大多靠经验完成,在海量数据中容易陷入局部极值解[12];粗糙集的最大优势是能处理不完整、不精确的数据,对不确定特征属性的识别具有一定帮助,但易受噪声影响,稳定性差[13-15]。由此可见,现有算法各有特色,但对于日渐庞大的数据规模和异常数据种类,采用信息熵作为目标函数完成异常数据的挖掘可以限定实际寻优范围。本文利用自主机器学习的数据挖掘技术实现多算法融合,设计了熵目标函数最优化算法。该算法的优势在于信息熵解算本身就是面向海量数据的,且是针对信息值的,不需要先验数据特征。
1 异常数据特征属性分类
1.1 样本属性分类
采用挖掘技术[16]中的聚类算法对异常数据进行特征聚类。设所有待检测数据点集合为M,其中存在N个异常数据样本集合。异常数据样本对应的权值为cj(t),j=1,2,…,K;异常数据聚类权值为c′i(t−1),i=1,2,…,K′。异常数据样本对应的权值由其可能造成的错误严重程度给出,通常由数据用户提供。将Kt个异常数据样本xj(1)归类到K个聚类中心,则异常数据聚类中心可表示为
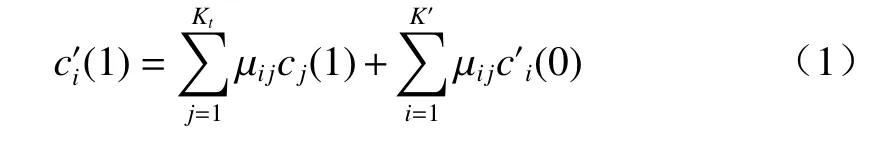
式中:μij是异常数据样本相对聚类中心的模糊隶属度(集合成员若被定义为0 或1,则成员介于[0,1]之间的集合可称之为“模糊隶属度”,用于表达具有不确定性的数据。),1≤i≤K′,1≤j≤Kt。
设存在n个d维的异常数据特征集合,表示为X=(x1,x2,…,xn),则每个特征xi所对应的密度指标可表示为

式中:ra为异常数据特征xi的邻域区间半径,设该区间中密度最大值为x1,则密度指标为D1。若xl是第l次的异常数据聚类中心,其密度指标有Dl,则(2)式有:
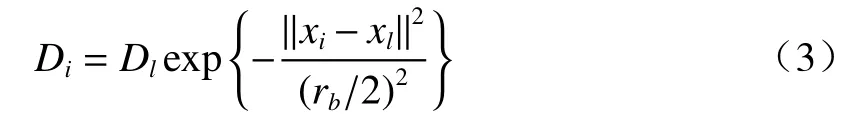
式中,rb为异常数据特征密度指标的邻域区间半径。由此可见,异常数据的特征可由Dk+1/D1的比值进行分选,比值越小,则其聚类结果越好。
1.2 特征提取优化
基于属性特征密度的判据可以完成特征分类,但是Dk+1/D1阈值的选取直接影响了聚类质量,故本文设计了利用高阶统计量作为模型补偿参数的特征提取优化算法。设数据集合为M={m1,m2,…,mm},个体最优解集合为Pi={pi1,pi2,…,pid},全局最优解集合为Pg={pg1,pg2,…,pgd},在则异常数据判断更新策略有
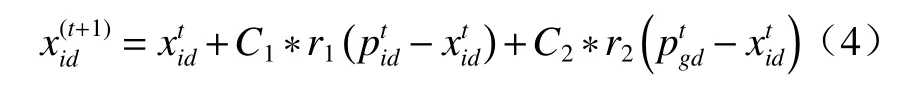
式中:xid表示第i个节点在第d维中的异常数据集合中的一个数据点;{C1,C2}为优化加速系数;{r1,r2}为[0,1]的随机值,由此构建的模型可使数据具有更好的相关性。首先,将求解分布聚类的最大值,有

然后,求解平均粒度,有:

式中:dij(t)为第j个采样点i维上的分布聚类;d为异常数据维度;m为总样本M中的数据个数。最后,设高阶统计量的数据聚类度是k,则其函数可表示为

对k值的循环迭代即可实现对特征提取参数优化选择。
2 异常数据检测与实现
2.1 函数构建
在上述异常数据特征优化提取的基础上,对光纤传感网络中的所有待测数据进行检测。由光纤故障导致的异常数据类型有很多,使异常数据的属性结构各不相同,故单纯采用传统的样本方差或平方差形式会造成识别误差大的问题。本文提出了基于熵目标函数最优化的异常数据检测算法,根据光纤网络中异常数据随机性强的特点,引入熵描述数据的不确定度,设t时刻异常数据特征为X(t),对第i个样本属性而言,P(xi(t))为样本属性xi(t)的概率,则熵H有:

结合样本方差S2有:

将(8)式和(9)式作为异常数据判别依据后,熵目标函数有:

式中:α和β为权重系数,α+β=1,α>0,β>0。该函数即为异常数据检测函数。
2.2 算法实现
为了获得光纤通信网络中异常数据识别的最优函数值,实现算法步骤如下:
1)在初始时刻t=0时,将光纤网络中已有的异常数据特征参数载入算法,自动检索半径设为R,信息特征阈值设为T,迭代次数为i;
2)将光纤网络中异常数据属性特征X(t)构建的目标函数F(xi(t))作为目标值,将τ设为目标的值,构建符合检索半径R的适应度函数:

3)带入初值后获得标的值的初值F(R,0),经过算法迭代令F(R,0)趋近F的全局最优解Fbest,从而得到f(R,0),判别依据有:

4)在所有待测数据集合M中循环运行(9)式和(10)式,从而获得Fbest和f(R,0),当f(R,τ)>f(R,0),更新Fbest和f(R,0);否则,进入下一个数据检测循环;
5)将P(xi(t))映射到搜索域中,导入下式:

将输出数据与f(R,0)进行比较,若大于f(R,0),用F(R,i)替换Fbest,f(R,i)替换f(R,0);若小于等于f(R,0),则设i=i+1,转入判断下一个数据的异常判断概率计算,直至结束;
6)循环得到迭代后的f(R,i),与T进行比较,当f(R,i)
7)将Fbest带入异常数据检测函数计算标的值,结束运行。
由此完成算法,流程图如图1所示。

图1 熵目标函数优化算法流程图Fig.1 Flow chart of optimization algorithm for entropy objective function
2.3 算法评价
为了验证算法具有更好的适用性,主要从数据融合率、检测精度、检测耗时以及误检率4个方面进行分析。数据融合率用于考察算法对不同数据的融合能力;检测精度用于考察对异常数据物理位置的计算精度;检测耗时用于描述算法的处理速度;误检率用于检出异常点与总点数之比,是最直接反映算法性能的评价参数。
3 实验
为了验证本算法的异常数据检测精度及运算速度,实验在VS2005 平台下利用C#语言完成。系统包括主频3.0 GHz的CPU、2 GB的内存和Xeon e5 型服务器。将异常数据状态信息、光时域反射仪(optical time domain reflectometer,OTDR)测试信息进行对比,从而进行评价。
3.1 数据状态分类
针对实验室光纤网络服务器系统2019年的通信记录信息,分别将状态信息、OTDR测试信息以及数据占用率等进行了对比,并按照光纤网络系统中不同的状态组合进行了对比,M{M1,M2,…,Mn}就是数据集合,则测试数据如表1所示。
对所有光纤通信网中的状态数据进行汇总,然后利用本算法进行分类识别,对异常数据进行标记,并与OTDR测试结果对比,分析算法数据识别的能力。为了保证训练效果,取50组正常数据(P)与50组各类不同异常数据(Q)构建样本,分别采用时序分析法(常用的数据规律统计方法,与其对比可以体现出本算法处理结果与数据统计规律的符合程度。)与BP神经网络(常用的参数权重调整方法,与其对比可以体现出本算法最终参数选择的适应度。)进行对比。

表1 异常数据与光纤网络状态测试表Table1 Abnormal data and fiber network state test
3.2 结果对比
验证集为1 000组随机通信数据,训练后分别求取3种算法的数据融合率、检测精度、检测耗时以及误检率,结果如图2所示。数据融合率为原始数据与融合数据之差再与原始数据的比,该指标反映了算法特征分类的能力。当在特征提取过程中选取的聚类精度不同时,相同属性的数据融合效果如图2(a)所示,3种方法结果在精度较低时相近,随着识别精度的提高,本算法略优于其它两种算法;如图2(b)所示,本算法的检测精度基本不随样本个数的增大而减小,其均值约为95.7%,时序法均值约为84.6%,BP神经网络法会随着数据量增大而明显下降;如图2(c)所示,本算法与BP神经网络法的收敛时间相近,时序法计算速度受样本总量的影响较大;如图2(d)所示,本算法和BP神经网络法的误检率波动较小,本算法效果最好,平均误检率仅为1.67%,BP神经网络法次之,为4.05%,而时序法受样本个数增加而出现较大偏差。综上所述,本算法对异常数据的属性分类具有很好的效果,在检测精度与误检率上相比传统方法均具有一定提升。

图2 不同算法数据处理性能对比Fig.2 Comparison of data processing performance by different algorithms
4 结论
本文提出了一种基于熵目标函数最优化的异常数据检测算法。利用对数据属性的特征分类完成对异常数据特征的提取,再通过高阶统计量的大数据聚类迭代完成样本数据熵目标函数的最优计算。实验对1 000组光纤通信数据进行分类,并与传统检测方法进行对比,结果显示,本算法在检测精度上具有明显优势,并且在数据融合率、检测耗时以及误检率方面也略强于传统算法,具有一定的应用价值。
