桥梁动态称重技术在中小跨径混凝土梁桥上的适用性研究

邓露，李树征，淡丹辉，赵华，余加勇，晏班夫

（1. 湖南大学 土木工程学院，湖南 长沙410082；2. 同济大学 桥梁工程系，上海200092）

随着交通运输业的迅速发展，桥上车辆荷载发生了很大的变化.一方面，车辆数量和载重量的大幅增长造成了实际交通荷载可能与桥梁结构设计荷载存在较大差异；另一方面，日益增多的车辆超载事件还可能会导致桥梁产生严重的损伤甚至发生失效事故，给桥梁安全带来巨大的威胁[1].快速识别车辆重量的技术可用于实际车辆荷载统计和超载车辆监测，该类技术的发展对于桥梁等公路设施的安全运营具有重要作用. 桥梁动态称重（Bridge Weigh-inmotion，BWIM）技术能够高效地识别正常行驶车辆的重量、轴距轴重分布信息，且具有安装、维护方便而且不需要中断交通的优点.Moses[2]于1979 年第一次提出了BWIM 的概念和算法，而后国内外学者开展了大量的研究，并开发了不同的BWIM 系统.早期的欧洲WIM（Weigh-in-Motion，WIM）规范[3]推荐以跨径5～15 m 的梁桥或涵洞作为BWIM 系统的测试载体，并初步明确了动态称重技术的识别精度等级.Oh[4]将BWIM 系统应用到一座跨径28 m 的T 梁桥，采用数值模拟方法得到三轴车重量识别误差为±8%.Kalin 等[5]测量了重量为40 吨的5 轴半挂车通过多座桥梁时的桥梁动应变，并利用BWIM 方法测量了车辆重量，发现BWIM 技术也适用于跨径达30.5 m的简支T 梁桥.Yu 等使用小波分析方法从桥梁整体响应中获得了车轴的纵向位置[6]，同时利用同一截面不同传感器的响应差异，识别出了车轴在桥梁上的横向位置[7]，而后利用识别的车轴信息识别出了车辆轴重.近几年，Yu 等[8]和任伟新等[9]国内外多位学者对BWIM 技术的发展历史和研究现状进行了总结.王宁波等[10]还研究了BWIM 技术适用的桥型范围，并探讨了现阶段能达到的测试精度水平.

我国桥梁中占比最大的桥梁类型为中小跨径混凝土桥梁，然而目前关于桥梁类型、桥梁跨径以及BWIM 技术方案等对识别精度和稳定性的综合性影响的研究还较少，已有研究中对于路面平整度、系统噪声等因素的影响作用的考虑也不够充分.

基于以上研究现状，本文建立了不同桥梁截面类型和跨径的9 座桥梁模型，利用车桥耦合振动数值模拟获得了桥梁在不同车辆模型作用下的动力响应，然后利用BWIM 算法计算了移动车辆的重量，最后基于误差分析对比研究了不同BWIM 技术方案在我国常见中小跨径混凝土梁桥上的测试精度和稳定性.研究中考虑了桥梁跨径、截面类型、车辆类型、传感器测点位置、路面平整度、测量噪声、行驶速度等因素的影响，结果可为工程应用中BWIM 系统的方案选择提供参考.

1 BWIM 技术的求解理论

1.1 基于Moses 算法的BWIM 技术

使用O’Brien 等[11]提出的“矩阵方法”可以标定出高精度的桥梁影响线，然后利用影响线加载法可以获得车辆过桥时桥梁响应的理论值；另一方面，桥梁实际响应还可以通过数值模拟或试验测量得到.当车辆轴重未知时，可基于桥梁响应理论值和实际值之差建立以未知轴重为变量的误差函数，然后通过求解误差函数最小值，获得车辆轴重的估计.实际误差函数E 的表达式如式（1）：

式中：K 表示总的时间步数；Sak为第k 个时间步的桥梁响应实测值；Sbk为第k 个时间步的桥梁响应理论值. 利用最小二乘法求解上式误差函数的最小值，可求得车辆轴重：

式中：P 为车辆的轴重向量；I 为基于荷载位置和影响线坐标建立的列满秩矩阵；Sb为桥梁响应的实测值向量，T 表示矩阵转置. 而后将算得的车辆各轴轴重进行叠加即可得车辆总重，表达式如下：

其中N 为车辆轴数.

1.2 基于应变面积法的BWIM 技术

应变面积法[12，13]是另一种求解车辆总重的方法.该方法基本思想为车辆荷载作用下的桥梁累积响应与车辆重量呈正相关，其不需要复杂的影响线标定过程.具体过程为令已知重量（记为GC）的标定车辆通过桥梁，记录桥梁的应变历程并进行积分得到积分值AC.而后只需记录待测车辆过桥时的桥梁应变历程和积分面积A，则待测车辆重量G 可由下式估计：

需要指出的是，尽管该方法名为应变面积法，但实际上，与Moses 方法一样，该方法也可利用桥梁挠度、支反力等其它类型的桥梁响应来进行车辆重量的识别.

2 车桥耦合振动仿真系统

车桥耦合数值仿真中，首先利用模态综合法降低耦合系统微分方程的规模，然后利用Newmark-β法求解模态坐标下的动力学方程，具体求解过程可参考文献[14，15].通过与实桥试验数据进行对比[15]，可知本文的车桥耦合仿真程序是较为准确和可靠的.

2.1 桥梁模型

本文从《公路桥梁结构上部构造系列通用设计图》（2010 年版）[16]中选取了9 座具有代表性的桥梁，并利用有限元分析软件ANSYS 建立了桥梁有限元模型，其中桥梁支承方式为两端简支，主梁和桥面板均采用Solid185 单元模拟，单元边长最大尺寸限制为0.2 m. 桥梁模型基本参数如表1 所示. 由表中可知，这些桥梁具有不同的截面类型、跨径和基频.桥梁跨中横截面及车辆横向加载位置如图1 所示.

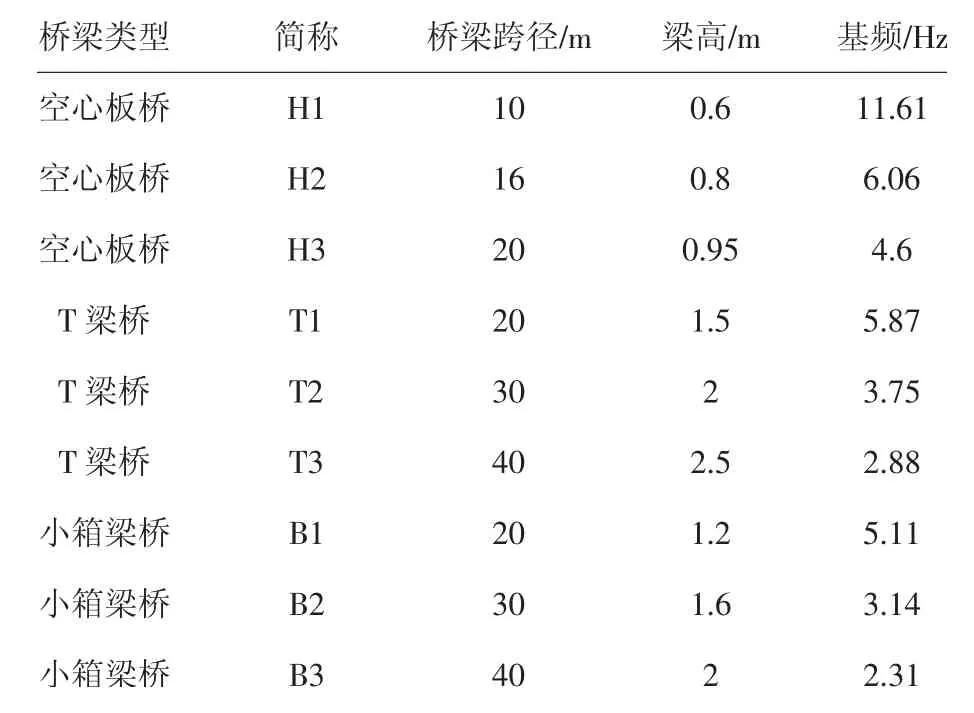
表1 桥梁模型参数Tab.1 Bridge model parameters

图1 桥梁跨中横断面图Fig.1 Cross section of bridges

2.2 车辆模型

本文选用三种车辆模型，分别是2 轴车[17]、3 轴车[18]以及能表征我国设计车辆荷载动力特性的5 轴车[19].车辆模型的总重分别为73.5 kN、320.1 kN、550 kN.仿真试验中，将2 轴车作为标定车辆，3 轴车和5轴车作为待测车辆.需要注意的是，由于五轴车的第二、三轴间距和四、五轴间距很小，均为1.4 m，利用BWIM 算法可能难以获得这些车轴的准确重量，此时，合理的做法是将紧密相临的多个车轴当做轴组处理[20].因此，在识别出该车车轴的各自重量后，将二、三轴的轴重相加，视为一个轴组的重量，四、五轴的轴重相加，视为另一个轴组的重量.后续的误差分析也是基于获得的轴组重量进行. 车辆模型的车轴位置和轴重如图2 所示.

图2 车辆模型（右视图和前视图）Fig.2 Vehicle models（right view and front view）

3 BWIM 技术适用性研究

3.1 工况设置

为研究BWIM 技术在不同类型中小跨径混凝土梁桥上的适用性，本文建立了9 座桥梁的有限元模型，每座桥梁选取了5 种不同的纵向测点位置，获得了测点位置的弯曲应变和桥梁挠度2 种桥梁响应，然后分别利用Moses 方法和应变面积法来进行车辆重量识别；研究中使用了3 种车辆模型、5 种车辆行驶速度、3 种等级的路面不平整度和4 种水平的输入噪声，输入噪声被假设为高斯白噪声，添加噪声的方法可参考文献[21].车桥耦合振动仿真的时间步长取为0.001 s，即采样频率为1000 Hz.由于通行车辆在中小跨径混凝土梁桥上通行时间很短（1～2 s），故假设车辆为匀速行驶且车辆行驶位置与标定车道一致，这也是众多研究普遍采用的假设.研究考虑的工况详细如表2 所示.其中，路面平整度根据我国GB 7031-1986 规范模拟.为减小路面平整度样本的随机性对识别结果的影响，对于每种等级的路面平整度，随机生成20 个路面样本并分别用于车桥耦合振动仿真，然后进行20 次独立的车辆重量识别，最后取20 次识别结果的统计值来进行后续的误差分析.

表2 数值模拟计算工况Tab.2 Values of parameters considered in case studies

3.2 车辆总重和轴重识别误差统计

欧洲WIM 规范[3]将车辆重量识别精度划分为如表3 所示的7 个等级，表中数值为各个等级的最大限值.

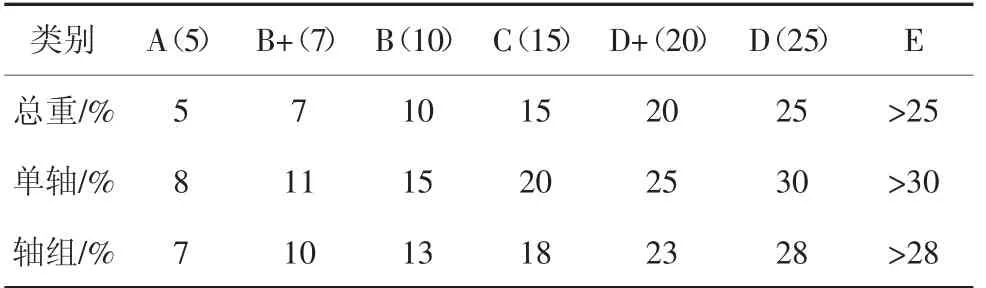
表3 WIM 测试精度等级表/%Tab.3 Test accuracy scale of WIM

为更细致地研究车辆总重识别误差的分布情况，将总重误差A（5）级别进一步细分为A（1）、A（2）、A（3）和A（5）等级，分别对应识别误差≤1%、≤2%、≤3%和≤5%.

图3 所示为数值模拟中共计216 000 次仿真试验中识别的车辆总重的误差分布图，其中左边的饼图为Moses 算法的识别结果，右边为应变面积法的识别结果.从图3 可以看出，对于所考虑的各种桥梁截面类型和桥梁跨度，两种车辆总重识别算法均可以获得理想的识别精度（＜3%）.当然，实桥应用时的识别精度一般不会如数值模拟般理想，但基于数值仿真，依然可以获得BWIM 方法在不同桥型、识别算法等因素影响下的相对表现. 例如从图3 还可以看出，Moses 算法识别结果达到A（1）级的占比94%，超过应变面积法的89%，且Moses 算法识别结果全部为A（2）级以上，不含A（3）级，这表明了Moses 算法识别车辆总重的效果整体上要优于应变面积法的识别效果.

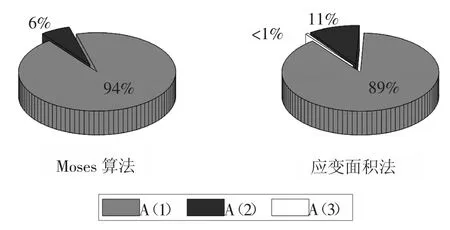
图3 不同算法识别车辆总重的误差分布Fig.3 Distribution of identification error of gross vehicle weight by different algorithms

由于应变面积法无法识别车辆轴重，而总重识别方面Moses 方法也要优于应变面积法，故后续关于车辆总重和轴重识别时均采用Moses 方法.表4 所示为使用Moses 算法识别的3 轴车和5 轴车各车轴及总重识别误差的有效值，由表中可以看到，两个车辆的后两轴（轴组）及总重的识别误差有效值都在5%以内，达到了A（5）级精度，而最轻的前轴（重约3吨）的识别误差分别超过了11%和25%，导致精度等级降至了B（10）和D（25）.其中，对于同一辆车，轴重越轻，识别误差越大，轴重越大，识别误差越小，且总重识别精度要高于轴重识别精度.注意到两辆车前轴的重量均为3 吨左右，但5 轴车前轴的识别误差却要远大于3 轴车前轴的识别误差，其中的原因可能是5 轴车前轴重量占整车总重的比例更小，为5.5%，而3 轴车前轴重量在整车重量中的占比为11.1%.另外，5 轴车的第2 轴组重达240.0 kN，大于3轴车第3 轴的142.4 kN，但后者的识别误差并未超过前者的识别误差，也表明了识别误差不仅与车轴的绝对重量相关，更多受车轴重量在整车重量中的占比影响.

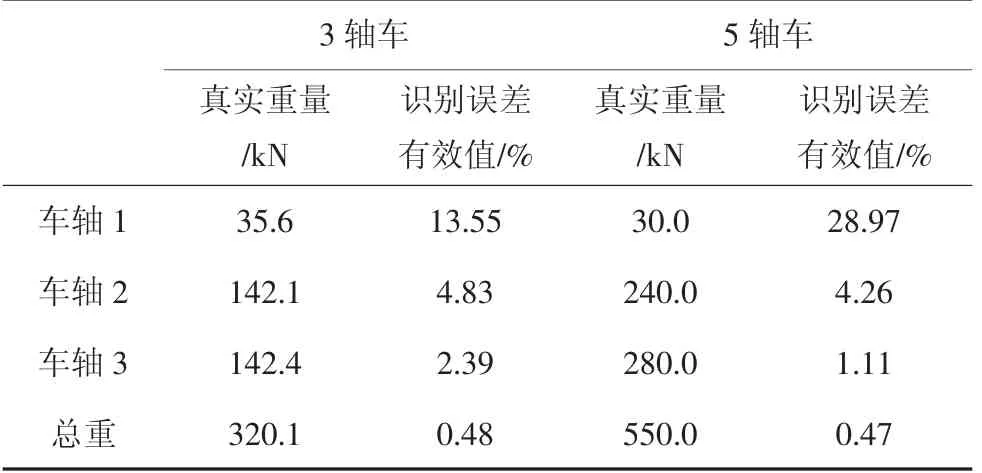
表4 车辆总重与轴重识别误差有效值Tab.4 The root mean square of identification error of gross vehicle weight and axle weight

3.3 桥梁跨径对识别效果的影响

图4 所示为3 轴车和5 轴车的总重和轴重识别误差有效值随桥梁跨径变化的情况.从图4 中发现，随着桥梁跨径的增大，车辆重量识别误差可能会迅速增大.为此，将基于不同跨径和不同截面的9 座桥梁识别出的车辆总重和轴重的识别误差有效值列于表5.由表中结果可以得知，车辆总重的识别效果受桥梁跨径和截面类型的影响较小，识别误差一直保持在0.5%左右，并不随跨径的增长而增大.

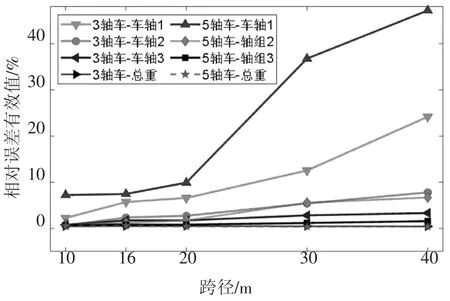
图4 不同跨径桥梁的车重识别误差Fig.4 Identification error of vehicle weight under different bridge span lengths

表5 不同跨径桥梁的车重识别误差Tab.5 Identification error of vehicle weight under different bridge span lengths

关于轴重识别，10 m 跨径空心板桥上的识别效果最好；16 m 和20 m 跨径的空心板桥上的识别精度也达到了欧洲WIM 规范中的最高A（5）级别；20 m跨径的T 梁桥和小箱梁桥的轴重识别误差略大，精度下降到B+（7）级；当跨径超过20 m 时，无论T 梁桥还是小箱梁桥，轴重识别精度均大幅下降，甚至部分识别误差已超过20%，不再具有良好的参考价值.显然，与总重识别不同的是，基本上，轴重识别误差会随桥梁跨径增长而明显增大，尤其较轻的前轴受影响最为明显，而最重的后轴所受影响则相对较小；另外，3 种不同类型的桥梁截面中，空心板桥的识别效果最好，T 梁桥次之，小箱梁桥的识别效果最次.

3.4 传感器测点位置对识别效果的影响

基于5 个不同纵向位置的桥梁响应识别的车辆总重和轴重的误差有效值如图5 和图6 所示. 从图中可以看到，对于3 种典型截面的梁桥，传感器测点位置变化时，总重和轴重识别误差基本上变化不大，表明在本文所研究的情况中，传感器纵向位置对重量识别的影响很小. 这可能是因为利用数值仿真模拟桥梁振动时，桥梁不同位置响应的模拟精度是基本一致的，故识别结果的精度也较为接近.值得注意的是，跨中位置的轴重识别精度略低于两侧，这与既往研究中普遍认为最优的传感器安装位置为跨中位置不同.不过，在实桥应用中，桥头搭板落差等其它局部缺陷可能对安装在其附近的传感器的信号测量产生不利的影响；此外，越接近桥梁端部，桥梁响应越小，对信号采集设备的要求也会越高，因此实际工程中应综合考虑各方面影响因素，选择合适的测点位置.

图5 不同传感器测点位置下总重识别误差Fig.5 Identification error of gross vehicle weight under different sensor installation positions

图6 不同传感器测点位置下轴重识别误差Fig.6 Identification error of axle weight under different sensor installation positions

3.5 路面平整度对识别效果的影响

车重识别误差随路面平整度变化情况如图7 和图8 所示.由图容易发现，对于车辆总重和轴重的识别，路面平整度越差，识别的相对误差也越大，其中“良好”路面等级下的识别效果和“中等”路面等级下的识别效果差异相对较小，而当路面状况劣化到“较差”等级时，识别误差会较为明显地增大.显然，作为车桥耦合振动的主要激励源，路面不平整会导致桥梁不规则振动，从而对车辆重量的识别产生影响，因此及时维护修缮桥梁，保持桥面平整对于获得可靠的车辆重量识别效果具有非常重要的意义.

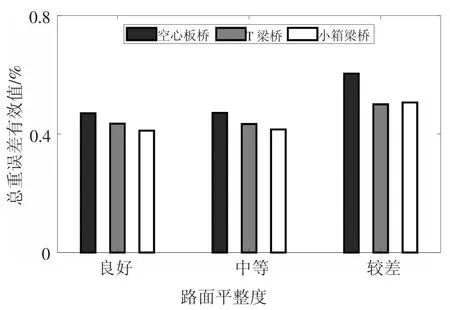
图7 不同路面平整度下总重识别误差Fig.7 Identification error of gross vehicle weight under different levels of road roughness

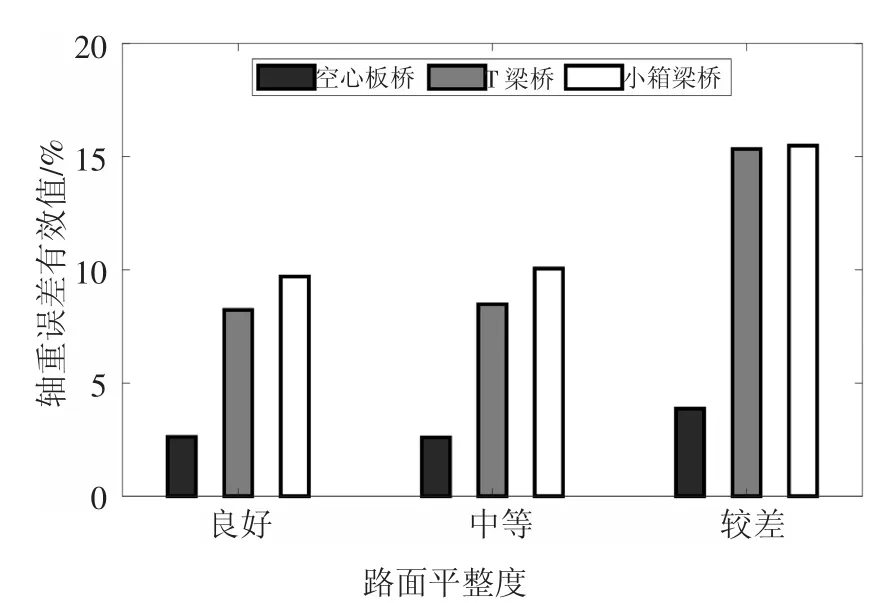
图8 不同路面平整度下轴重识别误差Fig.8 Identification error of axle weight under different levels of road roughness

3.6 车辆速度对识别效果的影响

图9 和图10 分别为车辆按不同速度行驶时，总重和轴重识别误差的有效值.由图可以看到，车速对车重识别误差的影响没有较为明确的规律. 对于不同的桥梁，识别误差的变化并不一致，峰/谷值对应的车速也不相同.尤其需要注意的是，更小的行驶速度，并不一定获得更小的识别误差，但基本上轴重识别误差的最大值均发生在车辆以30 m/s 的最高速度行驶时，因此，为了获得较好的轴重识别效果，可以适当对货车在测试路段的最高行驶速度进行一定的限制.

图9 不同车速下总重识别误差Fig.9 Identification error of gross vehicle weight under different vehicle speeds

图10 不同车速下轴重识别误差Fig.10 Identification error of axle weight under different vehicle speeds

3.7 输入噪声对识别效果的影响

图11 和图12 为输入信号中掺入不同水平噪声后的车重识别误差有效值.从图中可以发现，识别误差的大小与噪声水平呈正相关关系，其中，总重识别误差受噪声影响较为明显，当噪声水平从1%增长到10%时，识别误差有效值呈现了翻倍的增长；而轴重识别误差的增长则相对平缓，这可能是由于在众多因素的共同影响下，轴重识别误差的绝对大小较大，而输入信号的噪声在众多影响因素中并不占主导地位.不过尽管噪声水平增大到10%时，总重识别误差出现了明显增长的趋势，但实际上识别误差的有效值仍然小于1%；同时，尽管轴重识别误差也有一定程度增长，但利用跨径不大于20 m 的桥梁识别的轴重的误差均控制在了5%以内，表明BWIM 技术在输入噪声的干扰下仍具有较高的可靠性.

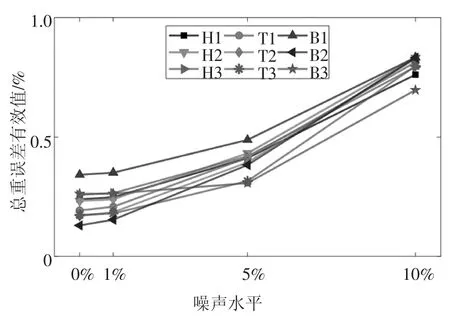
图11 不同噪声水平下总重识别误差Fig.11 Identification error of gross vehicle weight under different noise levels

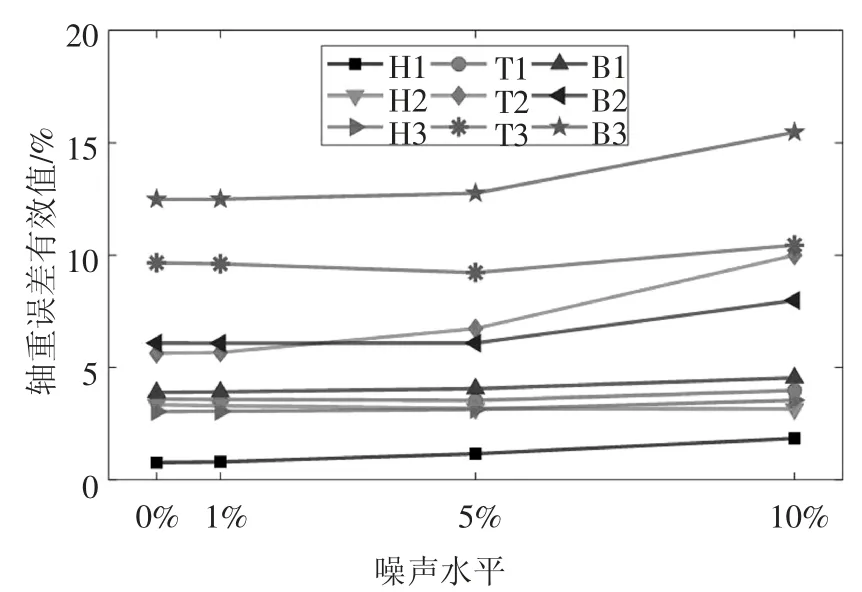
图12 不同噪声水平下轴重识别误差Fig12 Identification error of axle weight under different noise levels

4 结 论

通过建立不同截面类型和跨径的9 座混凝土桥梁模型，基于车桥耦合数值仿真技术对桥梁动态称重技术在我国典型中小跨径混凝土梁桥上的适用性进行了研究.获得的主要结论如下：

1）应变面积法和Moses 算法两种经典BWIM 算法都可以获得较为理想的总重识别精度，其中Moses算法的识别精度略高.基于BWIM 技术，我国常见的不同截面类型和跨径的混凝土梁桥，均适用于移动车辆总重的识别.

2）桥梁跨径越小，车辆轴重的识别精度越高；对于跨径在20 m 以内的桥梁，空心板桥的识别效果最好，而对于跨径大于20 m 的T 梁桥和小箱梁桥，前者的识别效果要好于后者.因此，将BWIM 系统应用于实际的公路梁桥时，首选的桥梁为小跨径的空心板桥，而当必须应用于较大跨径的梁桥时，则应优先选择T 梁桥.

3）路面不平整是影响BWIM 系统识别精度的重要因素.当路面状况劣化到一定程度时，车辆重量尤其是轴重的识别误差可能明显增大.因此，维护桥面平整对于保障BWIM 系统的识别效果具有重要意义.

4）输入信号噪声可能对车重识别效果产生不利的影响，不过对于本文研究的短跨径桥梁，车重识别误差均可控制在可接受的范围内.

5）BWIM 系统对于桥梁响应测点的纵向位置的敏感性较低，实际应用中并不需要严格要求传感器安装于桥梁跨中位置.

6）车辆速度对于车辆总重的识别精度的影响没有明确的规律，但对于研究中考虑的速度范围，总重识别均可获得良好的效果.另外，当速度超过一定范围时，可能导致轴重识别误差增大.因此，有必要对称重测试区段的货车行驶速度设定合理的上限值.

需要指出的是，上述结论是基于对单个车辆通过简支梁桥的研究而得出的.注意到Moses 算法本身是可适用于多车重量识别的，此时如何在复杂情况下获得准确的车辆速度和轴距信息将是重量识别的关键，因此BWIM 方法在复杂因素影响下的应用效果仍需要进行进一步的研究.