考虑数据异常及新旧程度影响有界性的地基沉降预测方法

曹文贵，谭涛

（湖南大学 岩土工程研究所，湖南 长沙410082）

众所周知，实测沉降数据是地基或路基沉降预测的基础，地基沉降预测的合理性除了取决于预测模型或方法与实测数据量的大小之外，还取决于实测数据的可靠程度及其新旧程度即实测数据点与预测点之间的时间距离，而且，实测数据新旧程度的影响并非无止境即存在有界性，也就是说，虽然实测与预测点之间的时间距离越小时，该实测点的数据应占有更高的权重，但是，这种影响并非随时间距离减小而无限增大，或者说，随时间距离增大而无限减小，因此，在进行地基或路基沉降合理预测时须对实测数据的可靠性与新旧程度影响的有界性予以充分重视，这正是本文研究的出发点.

目前，地基或路基沉降预测方法研究主要存在两条基本途径.其一就是单项模型预测方法，例如，双曲线模型、指数曲线模型、Asaoka 法、Logistic 模型、Weibull 模型、MMF 模型等[1-7]，其基本思路是依据地基或路基沉降发展变化规律，利用已有实测沉降数据或曲线，采用单一函数模型进行拟合以获得沉降与时间之间经验关系，进而实现对地基或路基沉降的预测. 该方法的突出优越性表现在分析计算简单，但其缺陷也是明显的，例如，预测精度或效果往往不尽如人意，而且，普遍适应性差.究其根本原因，由于地基或路基沉降发展变化的影响因素非常多且沉降机理复杂，难以找到具有普遍适用性的单项模型描述地基或路基沉降发展变化规律. 其二就是组合模型预测方法，例如，组合预测法、最优组合预测模型、非线性组合预测、变权重组合预测法等[8-15]，该方法的基本思路是考虑地基或路基沉降发展变化规律的复杂多样性，利用可描述不同沉降发展变化规律的多个单项模型，并依据各单项模型预测误差确定权重，实现对地基或路基沉降预测.该方法的突出优越性表现在其沉降预测精度或效果明显优于单项模型预测方法，其原因在于组合预测模型能反映地基或路基沉降发展变化规律和沉降力学机理的多样性，弥补了采用单项模型描述地基或路基沉降发展变化规律的片面性.因此，组合模型预测已成为目前地基或路基沉降的主流预测方法.

尽管如此，上述沉降组合模型预测方法并未考虑实测数据新旧程度对地基或路基沉降预测效果的影响，因此，曹文贵等[16-17]首次引进实测沉降数据新鲜度的概念，并采用诸如f（t）=t 的新鲜度函数描述实测沉降数据的新旧程度，提出了考虑实测数据新旧程度影响的地基或路基沉降预测新方法，这在一定程度上改善了沉降预测效果，但仍然存在明显不足.一方面，由于其采用的新鲜度函数是无界的，故无法反映实测数据新旧程度影响的客观有界性，也不能反映实测误差对新鲜度函数构建的影响，另一方面，没有考虑实测数据异常的影响.由于人为因素和沉降监测设备与方法可能引起的沉降监测系统误差，使不同实测沉降数据的可靠程度差别很大，明显不合理的实测数据参与沉降预测必然严重影响预测精度或效果，甚至引起沉降预测的谬误，故在进行地基或路基沉降预测之前，必须首先剔除这些不合理的异常数据.

综合上面所述，现有地基或路基沉降预测方法仍然存在较明显的不足与局限性，为此，本文将在地基或路基沉降组合模型预测方法研究基础上，重点考虑实测数据异常和新旧程度影响有界性对沉降组合预测的影响，对地基或路基沉降组合模型预测方法进行研究，以期完善地基或路基沉降预测的理论与方法.

1 沉降组合预测新方法

设已获得地基或路基实测沉降数据样本S（ti），它表示ti时刻对应的某点实测沉降（其中，i 为该实测点序号，i=1，2，…，N1；N1为实测点总数）.如果选取某单项预测模型j，可表示为

式中：Sj（t）为t 时刻某单项预测模型j 的沉降计算值；ajk对应于某单项预测模型j 的第k 个模型参数，k=1，2，…，N2；N2为单项预测模型参数的个数，并设由单项预测模型j 计算实测样本对应时刻沉降的误差平方和为Qj，可表示为

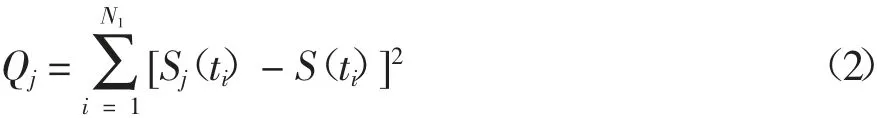
于是，依据最小二乘法原理[18]可得到

因此，由式（3）可得到N2个方程，将其联立求解即可确定出各单项预测模型j 的全部模型参数ajk，从而实现采用单项预测模型对t 时刻沉降进行预测.

考虑到沉降实测与预测点之间的时间距离不同对地基或路基沉降预测的影响不同以及不同单项预测模型对时间距离影响的依赖性不同，如果对应于单项预测模型j 选取不同的反映时间距离即实测数据新旧程度影响的新鲜度函数fj（t），则依据式（2）可获得反映实测数据新旧程度影响的地基或路基沉降预测的沉降误差平方和新函数Q′j，可表示为

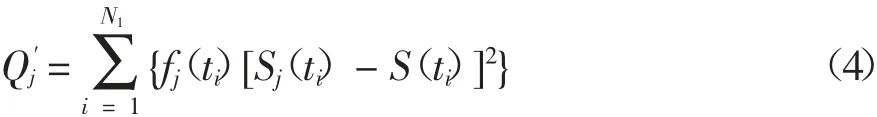
于是，依据式（4）按前述方法可确定出各单项模型j 参数ajk，进而可获得考虑实测数据新旧程度影响的地基或路基沉降预测方法，可表述为

式中：S′（t）、Sj（t）和ωj（t）分别为t 时刻地基或路基沉降组合预测模型与单项预测模型j 的预测值以及单项模型j 的权重，而且，各单项预测模型权重须满足

由此可以看出，为了利用式（5）预测t 时刻地基或路基沉降S′（t），尚需解决各单项预测模型权重ωj（t）的计算方法问题.为此，设ti时刻采用单项预测模型j 计算各实测点沉降的相对误差为Eji，可表示为

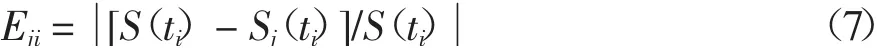
如果采用吻合度描述ti时刻由单项模型j 计算实测点i 沉降的吻合程度，并设其为cji，且其可表示为

于是，采用单项模型j 计算所有各测点沉降引起的总吻合度Cj可采用cji之和来度量，可表示为

很显然，Cj越大表示采用单项模型j 预测t 时刻沉降的准确度越高，则预测t 时刻沉降时，单项模型j 应该占有更高的权重，反之亦然.因此，预测t 时刻地基或路基沉降时，单项预测模型j 的权重ωj（t）可采用下式计算

至此已建立出考虑实测数据新旧程度影响的地基或路基沉降的组合预测模型即式（5）.值得注意，利用上述模型预测地基或路基沉降能否反映实测数据新旧程度及其影响程度有界性以及实测数据异常的影响，还须探讨实测数据新鲜度函数分析模型的构建方法及实测沉降数据异常的处理方法.

2 实测数据新鲜度函数模型构建方法

曹文贵等[16-17]提出了不同单项预测模型采用相同新鲜度函数f（t）=t 来描述实测数据新旧程度对沉降预测的影响，其虽然改善了地基或路基沉降预测效果，但明显存在不足，一方面，对于不同单项预测模型，采用相同新鲜度函数模型不能反映不同单项预测模型对实测数据新旧程度影响的差异性，第二方面，不能反映实测数据新旧程度影响的有界性；另一方面，不能反映不同时刻实测沉降与其客观沉降之间的差异对新鲜度函数模型的影响，因此，有必要重新探讨实测数据新鲜度函数分析模型的构建方法.为此，须首先掌握实测数据新鲜度函数分析模型具有的特性，因此，下面将进一步对此进行探讨.

1）反映时间距离即预测时刻t 与实测时刻tj之差的影响，而且，时间距离越大，则该实测沉降数据对沉降预测的重要性越低，反之亦然，也就是说，时间距离对地基或路基沉降预测的影响呈现单调变化规律；

2）反映tj时刻实测沉降误差的影响，而且，误差越大，该实测点沉降数据对沉降预测的重要性越大，反之亦然，也就是说，实测沉降误差对地基或路基沉降预测的影响也呈现单调变化规律；

3）不同时刻实测沉降数据对地基或路基沉降预测的影响程度是不同的，也就是说，不同实测点实测沉降数据的新鲜度是不同的；

4）实测沉降数据新鲜度对单项预测模型具有依赖性，也就是说，对于不同单项预测模型，相同时刻实测数据新鲜度是不同的；

5）实测沉降数据新旧程度对地基或路基沉降预测的影响并非无止境，也就是说，实测数据新鲜度函数分析模型是一个有界函数.

于是，考虑上述实测数据新鲜度函数分析模型的基本特性，经深入研究，本文构建出了新型实测数据新鲜度函数模型，可表示为

上述实测数据新鲜度函数分析模型具有如下特点：

1）由于Eji是根据单项模型j 计算出的ti时刻实测点的沉降误差，故反映了新鲜度对单项模型的依赖性，也反映了不同测点沉降误差对新鲜度影响的差异性，同时还反映了新鲜度随沉降误差增大而减小的内在规律.

2）由于t 和ti分别为预测点和实测点时间，故（ti-t）/t 体现了实测点与预测点之间的时间长度大小即实测点沉降数据的新旧程度，而且，也由于（ti-t）/t 必然为负值，e（ti-t）/t必然随ti增大而增大，故也反映了越新的实测点沉降数据对沉降预测的影响越大的合理客观现象.

3）由于0 ≤ti＜t，因此，e（ti-t）/t必然是一个有界函数，因此，fj（ti）也必然是一个有界函数，故本文建立的新鲜度函数反映了实测沉降数据新旧程度对沉降预测影响的有界性.

由此可以看出，本文实测数据新鲜度函数分析模型明显较曹文贵等[16-17]提出的仅能反映时间距离影响的新鲜度函数分析模型更具合理性.

3 实测沉降数据异常的处理方法

在进行地基或路基沉降监测时，由于人为因素或监测设备操作与测量方法不当，难以避免实测沉降数据的异常或不真实，如果不作处理直接将全部实测数据参与地基或路基沉降预测，必然会导致地基或路基沉降预测结果的不合理甚至谬误.因此，在预测出某时刻t 地基或路基沉降之前须剔除这些异常实测沉降数据.为此，下面将依据统计学理论探讨实测沉降数据异常的处理方法.

如果设由t 时刻组合预测模型计算得到的实测时刻tk的沉降为S″（tk），则tk时刻沉降实测相对误差E″（tk）可表示为

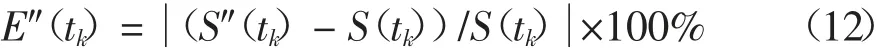
而E″（tk）的标准差σ 可表示为

式中：μ 为t 时刻沉降组合预测的相对误差E″（tk）的平均值，可表示为

于是，依据统计学理论的“3σ”原则[19]，当E″（tk）∈[μ-3σ，μ+3σ]时，tk时刻实测沉降数据合理，应参与t 时刻沉降组合预测，否则应将其剔除即不参与沉降预测，也就是说，t 时刻沉降预测的实测沉降数据样本大小应为N1-1.

值得注意，由于σ 和μ 与参与t 时刻沉降组合预测的实测沉降数据样本直接相关，因此，必须采用迭代分析方法进行反复迭代计算，直至完全满足上述条件为止，此时依据异常实测沉降数据处理后的实测沉降数据样本进行沉降预测，方可获得最终地基或路基沉降的合理预测结果.另外还须注意，利用“3σ”原则剔除异常数据时，需要有足够大的数据样本，这也是合理沉降预测的基本前提条件，否则，无法进行沉降预测.

4 工程实例分析与验证

上述已建立出考虑实测数据异常与新旧程度影响有界性的地基沉降预测新方法，但其可行性与合理性仍需验证.为此，本文将采用两个工程的实测沉降资料进行分析.

工程实例一为杭浦高速公路K90+769～K111+419 段[20]，工程实例二为深圳滨海大道K1+800 测试段沉降板T11 沉降实测结果[21]，其实测沉降数据如表1 所示.由于要验证本文方法的合理性，只能由理论预测与实测结果进行比较分析，因此，须将两个工程的实测数据分为两部分，第一部分作为沉降预测的原始数据样本，第二部分作为预测与实测的比较数据，因此，对于工程实例一和二，分别取前11 和15组数据作为原始数据，即对应N1分别为11 和15.

为了进行沉降预测，首先要选定若干单项预测模型，于是，通过对两个工程实测沉降曲线变化规律进行分析，选定Logistic 模型[4]、Weibull 模型[5]、MMF模型[6]3 个单项沉降预测模型进行组合模型预测（即N2=3），其中，Logistic 模型[4]可表示为

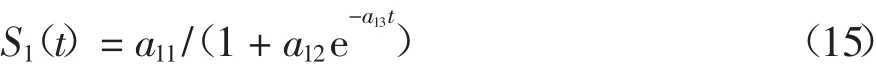
Weibull 模型[5]可表示为

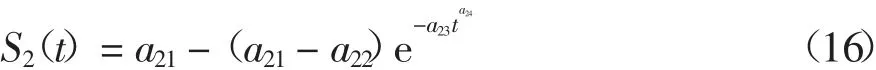
MMF 模型[6]可表示为

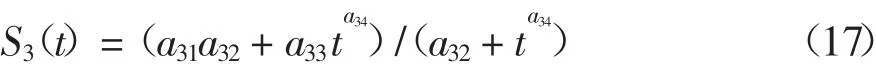
表1 工后沉降实测数据[20-21]Tab.1 Measured post-construction settlement

针对这两个工程实例的各预测时刻tk，采用本文模型与方法进行迭代计算可获得最终各单项模型参数与沉降组合预测结果，如表2 所示.并与现有相关预测模型的预测结果进行比较分析，如图1 和图2所示.由此可以看出，本文方法较现有同类方法的沉降预测精度或效果更好，表明了本文方法的合理性与优越性.

图1 工程实例一理论预测曲线与实测沉降曲线比较Fig.1 Comparison between predicted and measured settlement curves in Project No.1

表2 模型参数与沉降预测结果Tab.2 Model parameters and settlement prediction results

图2 工程实例二理论预测与实测沉降曲线比较Fig.2 Comparison between predicted and measured settlement curves in Project No.2

5 结 论

本文在现有组合模型沉降预测方法研究基础上，重点考虑实测沉降数据异常与新旧程度及其影响程度有界性对地基或路基沉降预测精度和效果的影响，进一步深入探讨了地基或路基沉降预测的模型与方法.由此可得如下结论：

1）构建了新型沉降实测数据的新鲜度函数分析模型，它不仅可反映实测沉降数据的时间距离与误差对单项预测模型的依赖性的影响，还可体现不同实测点数据的新鲜度函数不同以及新鲜度的影响程度有界性的特点.

2）基于统计学理论，提出了实测沉降数据样本的数据处理方法，避免了异常实测沉降数据导致地基或路基沉降预测精度下降甚至谬误的不合理现象.

3）在上述模型与方法研究中，引进组合预测理论，建立了新型地基或路基沉降预测新方法，并通过工程实例计算以及本文与现有同类方法预测和实测结果的比较分析，表明了本文模型与方法的合理性与优越性.

4）值得注意，本文模型与方法的沉降预测精度和效果与所选择单项预测模型的种类和数量直接相关，在实际工程应用中，应予以高度重视.