挡墙后有限宽度土体土拱效应分析及土压力计算方法

2020-04-11杨明辉吴志勇赵明华

湖南大学学报（自然科学版） 2020年3期

杨明辉，吴志勇，赵明华

（湖南大学岩土工程研究所，湖南长沙410082）

作用于结构物上的土压力计算是岩土工程的经典问题之一，其大小的合理取值是结构物设计的重要依据[1]. 目前传统的土压力计算大多采用经典朗肯、库仑土压力理论或基于经典理论修正的经验公式[2]，但均建立在墙后填土为半无限空间体的基本假定基础上.随着城市建设的发展，很多支挡工程中出现挡墙后填土宽度有限的情况，例如临近既有地下室基坑支护结构、临近基岩面的边坡挡土墙、地铁车站狭窄基坑支护结构等[3-5].此时，经典土压力理论显然并不适用于有限宽度土体的土压力计算，需要寻求更为合理的计算方法.同时，有限宽度挡土墙墙背并非绝对光滑，朗肯土压力理论假定墙背绝对光滑，从而忽略了墙土摩擦力的影响.而墙土间摩擦的存在必将引起土体应力偏转而形成土拱现象[6]，从而对土压力的分布产生影响.显然，对于墙后填土为有限宽度情况下，考虑土拱效应及土体宽度的影响对于更合理的计算土压力值十分必要.

目前，已有不少国内外学者将土拱效应成功地应用于土压力计算中，如Handy[7]将土拱定义为小主应力的轨迹，假定两平行粗糙墙间土拱的形状为悬链线，经过严密数学推导后得到墙后土压力分布；Paik 等[8]将土拱曲线简化为圆弧曲线形状，分别以挡土墙面和朗肯滑裂面作为两端拱脚，从而导出考虑土拱效应的刚性挡土墙主动土压力计算公式；尹志强等[9]以黏性填土的单排支护桩为研究对象，借鉴并改进了挡土墙的主应力偏转理论，推导出了黏性填土排桩桩后土压力的解析式，且认为土拱效应主要影响桩体H/3 深度以下部分，使该部分土压力减小，且越靠近桩底，减小速率越大；刘洋等[10]考虑条间剪切应力的影响，通过对滑动土体中二维微分单元的受力分析建立平衡微分方程，推导出土拱曲线的解析表达式，在此基础上提出一个实用的土压力计算公式.

同时，针对墙后有限土体土压力计算的研究也取得了众多研究成果.如Greco V[11-12]针对无黏性土填土的有限宽度挡墙，提出多折线的土体破坏模式，采用极限平衡法推导出有限宽度土体土压力的计算公式；Frydman 等[13]通过离心机试验模拟了临近基岩面的刚性挡土墙，推导出谷仓土压力公式用以计算临近基岩面挡土墙的无黏性土静止和主动土压力；Fan 等[14]采用有限元研究了临近倾斜基岩面刚性挡土墙上主动土压力的分布；应宏伟等[15]对不同宽度的深基坑进行数值模拟，提出了考虑基坑宽度影响的基坑坑底抗隆起稳定分析模式，并修正了狭窄基坑被动侧的被动土压力系数；刘忠玉[16]以墙背和稳定岩质坡面间为有限无黏性填土的刚性挡土墙为研究对象，假定在平面应变条件下，墙体破坏模式为直线形或折线形滑裂面，考虑滑动土楔内水平土层间存在的平均剪应力，得到非线性分布的主动土压力表达式. 但以上研究基本前提仍假定土体破坏为直线破坏模式，而很多研究均表明墙后土体的滑裂面将会是曲面[17-18].杨明辉等[19]开展了刚性挡墙三种不同变位模式情况下墙后有限宽度土体破坏试验，得到了墙后填土宽度较小情况下的土体破坏模式，并提出了墙体平动变位模式下土体曲线滑裂面为对数螺旋线的结论[20-21].

综上，虽然墙后有限土体土压力计算在试验和理论计算方面已有不少研究，但缺乏对于此种情况下挡墙后土体土拱效应的分析.因此，为更合理地计算土压力的分布情况，本文通过解析方法，将对土拱效应的分析运用到墙后有限宽度土体的土压力计算问题中，并针对具体的土体曲线破坏面模式，提出在曲线破坏模式下相应的主动土压力计算方法，并深入讨论土体有限宽度的界定方法，以供相关工程设计参考.

1 墙后有限宽度土体情况土拱效应

众所周知，当墙体产生背离土体方向位移时，墙后变形土体将与稳定土体产生剪切摩擦，从而使变形土体承受的土压力转移至周围稳定土体区域，形成土拱.在挡土墙问题中，若墙背非绝对光滑，墙土摩擦以及变形土体与稳定土体之间的摩擦必将引起土体应力偏转，土拱效应是客观存在的[6].而对于墙后土体宽度狭窄时，由于墙体的侧向挤压作用更易形成土拱，从而对土压力的分布产生影响.因此，将土拱理论应用到有限宽度土体土压力计算问题中进行分析更为合理.

1.1 应力状态分析

Terzaghi 通过活动门试验证明了土拱效应，并将其定义为土压力从屈服区域转移到邻近静止区域的现象.

墙体与已有建筑物地下墙之间有限土体受力的应力偏转如图1（a）所示.为简便起见，设土体为无黏性土，土体重度为γ，内摩擦角为φ，墙土摩擦角为δ，变形土体达到主动极限应力状态时，墙土摩擦力充分发挥.当挡土墙为静止状态、挡土墙和填土的沉降相等时，墙土之间无摩擦，则填土中的微分单元体之大小主应力分别为竖直方向和水平方向.

图1 有限宽度土体土拱效应分析Fig.1 Analysis of soil arching effect in finite width soil

随着支护结构的侧移，土体逐渐出现竖向变形，墙土及土体内部剪切滑裂面摩擦力逐渐发挥作用，直至其墙后土体处于极限平衡状态时.此时，假定有限土体产生足够的竖向变形，墙土摩擦力充分发挥，根据土拱原理，墙体相邻土体的微元之大小主应力由于受到剪切力的影响，主应力发生旋转，其主应力的方向与竖直或水平方向出现一个夹角，变形区的土体将产生应力偏转. 支护结构AB 与剪切滑裂面BC 之间土体达到塑性平衡状态，DF 之间各点的小主应力轨迹将形成一条连续的拱曲线，这时的小主应力轨迹线为一条下凸曲线.

1.2 应力偏转角

支护结构所承受土压力即为墙后土体水平向的侧向压力，因此土压力计算的关键在于求解支护结构之后土体的水平方向应力，但此时由于应力偏转，水平向应力已不是最小主应力，所以首先得求出应力偏转角.

如图1（a）所示，高度H 的挡墙后土体达到主动极限平衡形成土拱. 在距填土表面y 处取宽dy 的水平向土条，长度L.为简化计算，采用与Paik 等[8]相同的圆弧拱，圆弧拱的圆心位于图中的O 点，半径为R，作用在水平微单元体上的大主应力正交于虚线表示的土拱迹线，而虚线表示的土拱线即是小主应力轨迹. 圆弧拱起始点D 和圆心O 连线与水平方向成角θ，滑裂面上任意一点处的切线与水平方向夹角为α.如果墙面光滑，此时不能形成土拱效应，圆心O 将位于无限远处.在未变形前的土条中E 点取宽度dA的微单元，该单元所受竖向合力dV，该点变形后和圆心O 的连线与水平方向夹角Φ.

图1（a）中D 点主动破坏时的Mohr 应力圆如图1（c）所示，σv是主动破坏时D点的竖向应力，σh是主动破坏时D点的侧向应力，墙土界面处土体所受摩擦力τD方向向上. 从图中的几何关系可以得到D 点的应力关系，主动破坏时：

无论土体主动、被动极限平衡时，都有大小主应力比值E 为：

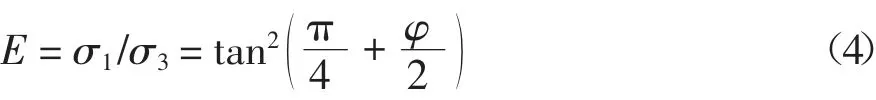
式中：φ 是墙后土体内摩擦角.

由式（1）可得，在圆弧拱的D 点有：

同理可得，E 点主动破坏时：

其中墙土间摩擦力的关系如下：

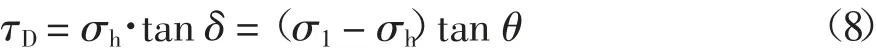
式中：δ 是墙土界面摩擦角，则有：

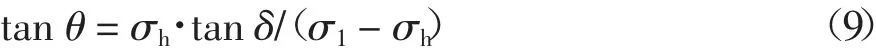
式（9）右端分子分母同除以σ1，将式（1）代入式（9）得：

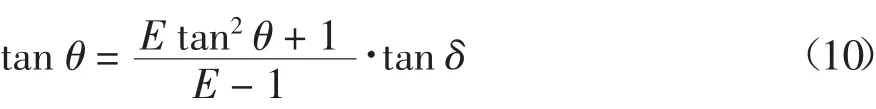
解得主动破坏时的偏转角θ：

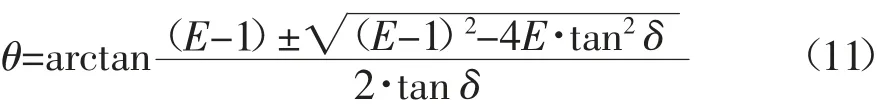
如图1（a）所示，由于墙土摩擦角的作用，墙背D点的主应力方向已逐渐发生偏转，作用在墙背的水平向应力已经不再是小主应力.在挡墙任意深度y 处D、F 两点的小主应力轨迹形成了一条圆弧拱曲线，即为小主应力拱.在破裂面上，由极限平衡条件可知大主应力作用面与破裂面切线的夹角为β=π/4+φ/2.

2 主动土压力计算

2.1 墙后土体滑裂面方程

在墙后有限宽度土体的情况下，已有室内模型试验表明[18]，当挡土墙在平动模式下背离填土方向达到主动极限平衡状态时，墙后有限宽度无黏土的滑裂面曲线为一条通过墙趾的对数螺旋线，滑裂面方程为：

因此，本文以该土体曲线滑裂面为例，对土压力分布进行求解.在图2 所示的极坐标系中，墙后填土产生的对数螺旋滑裂面方程直角坐标为：

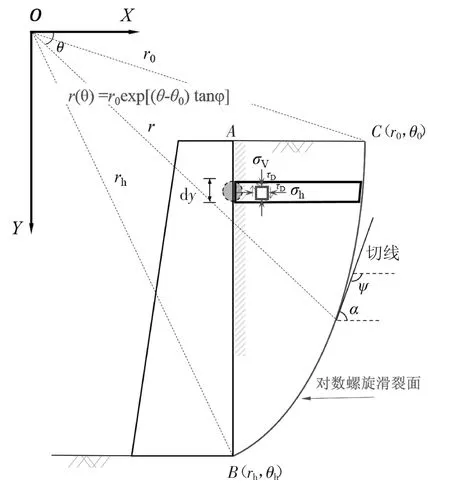
图2 对数螺旋滑裂面坐标系Fig.2 Logarithmic spiral slipping surface coordinate system

设对数螺旋线上某一点的斜率为k，切角为ψ，则有：

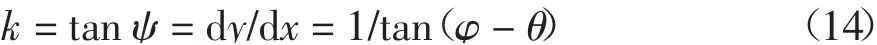
式中：α 为滑裂面上任意一点切线与水平方向夹角.

在图1（a）中，F 点大主应力与水平方向的夹角φ2可由式（15）求得：

2.2 主动侧向土压力系数

在得出墙后土体的滑裂面形状后，即可对墙后土体的土压力分布进行分析.

由图1（a）可知，小主应力轨迹线上任意一点E所受到的竖向力dV 为：

式中：R 为任意深度y 处的小主应力圆弧拱半径，如图1（a）所示，可用该深度处土体宽度L 表示为：

由式（15）、（16）、（17）可得，y 深度处微分单元的平均竖向应力为：

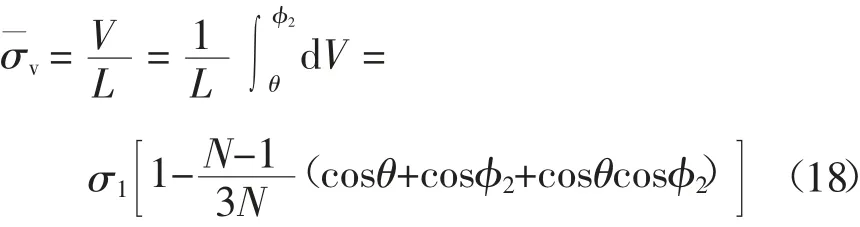
式中：V 为y 深度处微分单元所受的总竖向力.

由式（6）和式（18）可得到侧向主动土压力系数为：

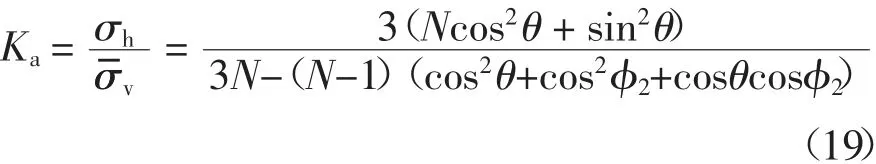
2.3 主动土压力合力及其分布

在距滑楔体表面y 处取一厚度为dy 的水平微分单元abcd，水平微分单元的受力如图3 所示.σv为作用于水平微分单元顶面的平均竖向应力，σv+dσ v 为作用于水平微分单元底面的平均竖向应力.σh为挡土墙的水平反力，τD为作用在挡土墙上墙土摩擦力.σn为不动土体对滑楔体在垂直于破裂面上的反力，τf为不动土体对滑楔体的摩擦力，dW 为水平微分单元自重.当dy 足够小时，bd 可近似为直线，α 为水平微分单元破裂面与水平面的夹角，易得：

图3 水平微分单元Fig.3 The horizontal differential element

水平微分单元上表面长度：

水平微分单元下表面长度：

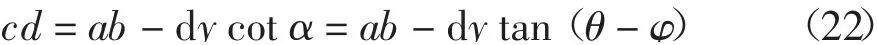
则由式（21）、（22）可得水平微分单元的自重为：

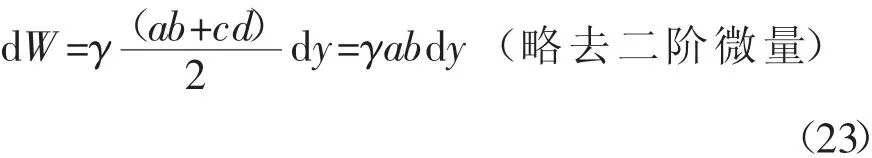
由微分单元水平方向上力的平衡条件可得：

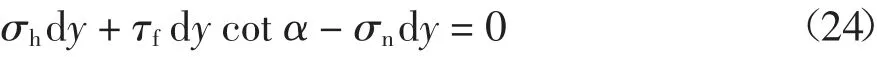
即

由微分单元竖直方向力的平衡条件可得：

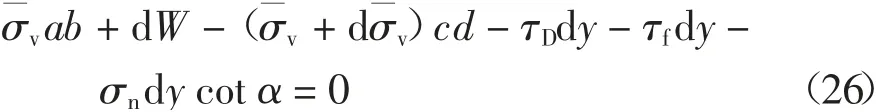
将ab、cd、dW、α 代入式（26）并略去二阶微量可得：

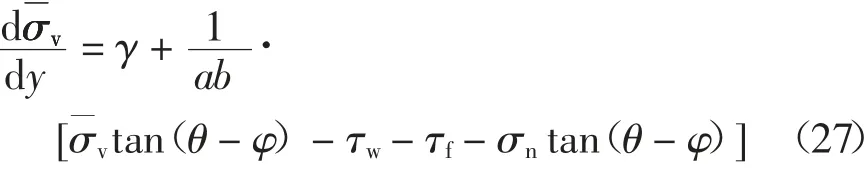
联立式（20）、（21）、（27）可得到求解微分单元平均竖向应力σv的基本方程为：

解微分方程，并结合边界条件：y=r0sin θ0时，σv=0.

则微分单元的平均竖向应力为：

由此可得主动土压力强度分布方程为：

则挡土墙土压力合力为：

而挡土墙土压力合力作用点至墙踵的距离为：

式中：y1=r0sin θ0，y2=rhsin θh=r0exp [（θh-θ0）tan φ]sin θh.

根据图1（a）的几何关系得到：

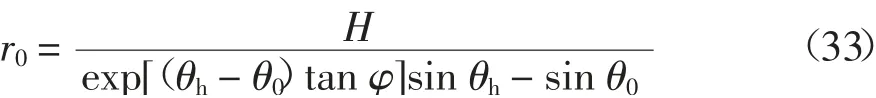
填土宽高比为：

将式（33）、（34）代入式（31）得：

上式即为墙后有限宽度土体情况下土压力的隐式表达式. 由上式可见，Ea值与δ，φ，γ，n，H 以及θh相关，但其中仅θh未知.由对数螺旋方程性质可知：

式中：θB为墙踵处滑裂面切线与水平方向的夹角.

由文献[19]试验现象3 可知，土体破坏线始终位于库仑破坏线内侧，同时破坏线的破坏角θB始终大于库仑剪切破坏角θcr，即θB＞θcr.且当墙后填土为有限宽度时，二者的差距更大，这与文献[22]的结论一致.故由式（36）可知，θh＜π/2+φ-θcr=π/4+φ/2，θh的取值将小于π/4+φ/2.图4 为Ea随θh的变化曲线（n=0.1），由图可见，二者为单调递增函数.所以θh取π/4+φ/2 时求得的Ea是偏于安全的，可供设计时参考.

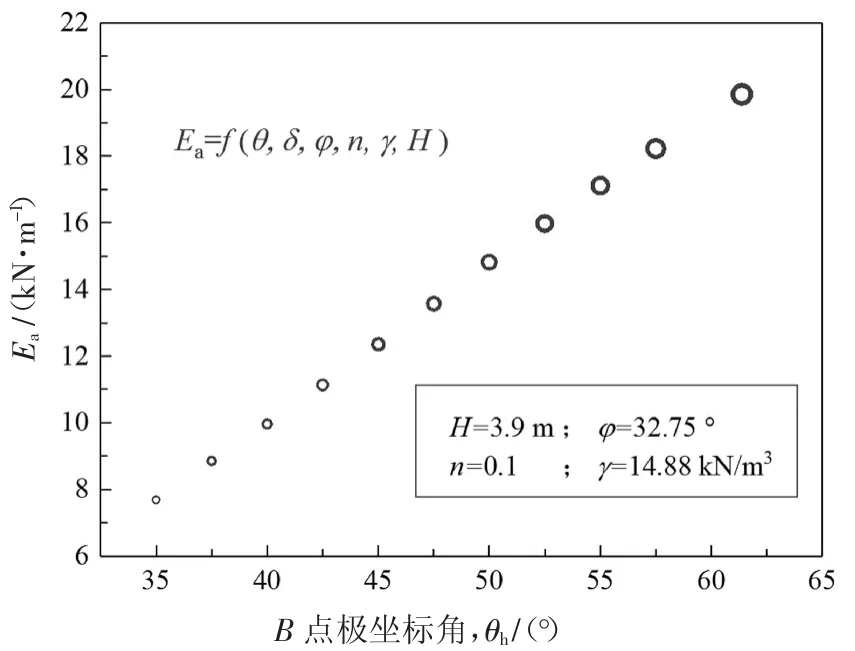
图4 主动土压力Ea 与θh 的关系曲线Fig.4 The curve of the relationship between Ea and θh

由此可得到土体的主动土压力强度分布，与笔者的室内模型试验数据[19]对比，如图5 所示.当墙后填土为有限宽度时，挡墙上水平土压力强度呈非线性鼓形分布，可见理论计算与试验结果[19]非常吻合.

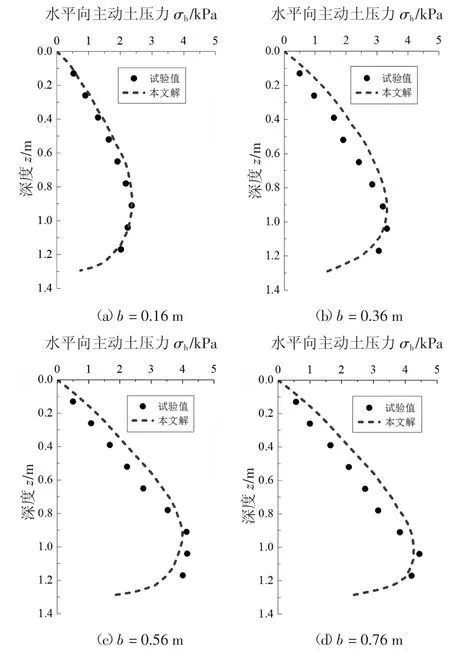
图5 主动土压力侧向力沿深度的分布与试验值[19]对比Fig.5 The comparison between distribution of lateral force of active earth pressure along depth and tested value

3 前人方法比较

3.1 Frydman 和Keissar[13]的模型试验

在Frydman 和Keissar[13]的离心机模型试验中，墙背和岩面竖直，无黏性填料的最大和最小干密度分别为1.64 g/cm3和1.40 g/cm3，填料的相对密实度为70%，内摩擦角φ=36°，填料与铝制挡土墙之间的摩擦角δ1=22°～25°，与模型箱之间的摩擦角δ2=30°，测得的主动土压力试验值见图6.

Frydman 等[13]将Janssen[23]的谷仓侧向压力计算公式在应用于计算极限土压力时对其中的侧压力系数进行修正，取φ=36°对试验结果按其修正公式进行了模拟，其结果如图6 所示.图中为填土宽度b=1 m 时的本文解、Frydman 修正解、Coulomb 解以及离心试验数据的对比.虽然试验点比较离散，但本文解与Frydman 修正解的计算结果吻合较好，基本上可描述主动土压力与深度的关系.对比两者可以发现，本文计算的土压力值大于Frydman 的修正值，可能的原因为计算土压力值采用的是θh取π/4+φ/2 时的假设，故本文求得的土压力值是偏于安全的.随着深度（y/b）增加至约6.3 处，本文计算的土压力值开始出现小于Frydman 修正理论值的趋势.

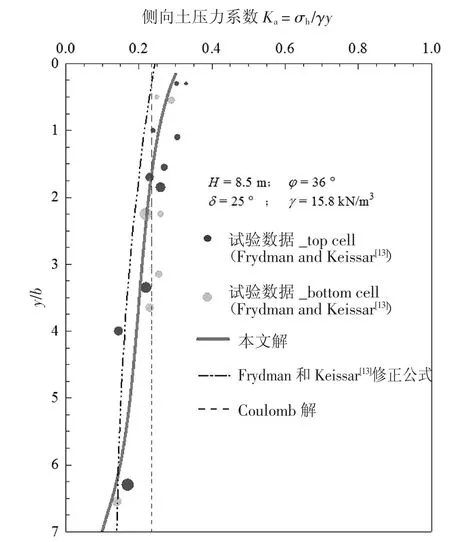
图6 侧向压力系数沿归一化深度的变化Fig.6 Variation of lateral pressure coefficient along normalized depth

3.2 Take 和Valsangkar[24]的模型试验

Take 和Valsangkar[24]的离心机模型试验描述的是墙背和岩面都竖直的工况. 无黏性填料的最大和最小干密度分别为1.62 g/cm3和1.34 g/cm3，填料的相对密实度为79%，峰值和临界状态对应的内摩擦角分别为36°和29°，填料与铝制挡土墙之间摩擦角的峰值和临界值分别为25°和23°，试验加速度为35.7g（g 为重力加速度），这样高度为140 mm 的模型挡土墙相当于5 m 高的原型墙. 填土宽度分别取L=15 mm、38 mm，相当于填土宽度b=0.53 m、1.36 m，测得的土压力值见图7. 这里取φ=29°、δ=23°按本文理论解进行了模拟，由图可知，试验结果与Take 和Valsangkar[24]的离心机模型试验结果比较接近.

图7 本文解与Take 和Valsangkar[24]实测值对比Fig.7 Comparison between experimental results of Take and Valsangkar[24]and thoeretical predictions

4 有限宽度土体的临界宽高比

4.1 宽高比临界值

墙后有限宽度土体的问题早已引起众多学者的关注，但有限宽度与无限宽度的界定一直缺乏较准确合理的取值. 大多学者根据库仑土压力理论计算的宽度作为临界值，但由于库仑土压力的直线破裂面假设的缺陷，该值并不准确.为此，本文采用逐渐逼近的方法，深入探讨了临界值问题.具体方法为：填土宽高比n 取值由小逐渐变大，分别求出对应的土压力强度分布，当土压力强度趋于稳定时，对应的宽高比为临界宽高比，相应的土压力值为无限填土的土压力值.

取基本参数如下：挡土墙高度H=1.3 m，填土重度γ = 14.58 kN/m3，内摩擦角φ = 32.75°，δ =21.83°，填土表面水平，宽高比n 取值从0.1 至0.6，间隔为0.1，计算结果如图8（a）所示.

由图可知，随着填土宽高比的增大，主动土压值逐渐增大，且增大幅度越来越小，当填土宽高比n≥0.5 时，主动土压力值基本保持不变，此时即为有限宽度填土和无限宽度的临界值. 若根据库仑土压力理论，得出临界填土宽高比ncr=0.67，可见经典的库仑土压力理论夸大了土体破坏宽度.

4.2 有限宽度临界值的参数分析

图8（b）是在不同的挡墙高度H 下主动土压力Ea随着宽高比n 的变化曲线.参数假定为：内摩擦角φ=32.75°，墙土摩擦角δ=φ，填土重度γ=14.88 kN/m3，挡土墙高度分别为H=3 m、4 m、5 m、6 m，宽高比n 的变化范围为0.1～0.8.由图可知，随着挡土墙高度的增大，主动土压力值显著增大.在不同的挡土墙高度下，主动土压力值随宽高比的变化均呈先单调递增，但变化幅度不明显，之后趋于稳定的土压力值. 主动土压力值基本保持不变时的宽高比为n=0.5，即为有限宽度临界值.

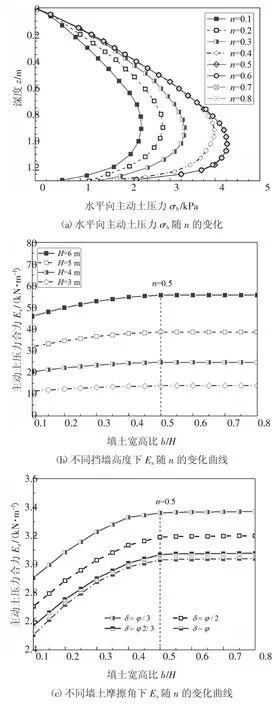
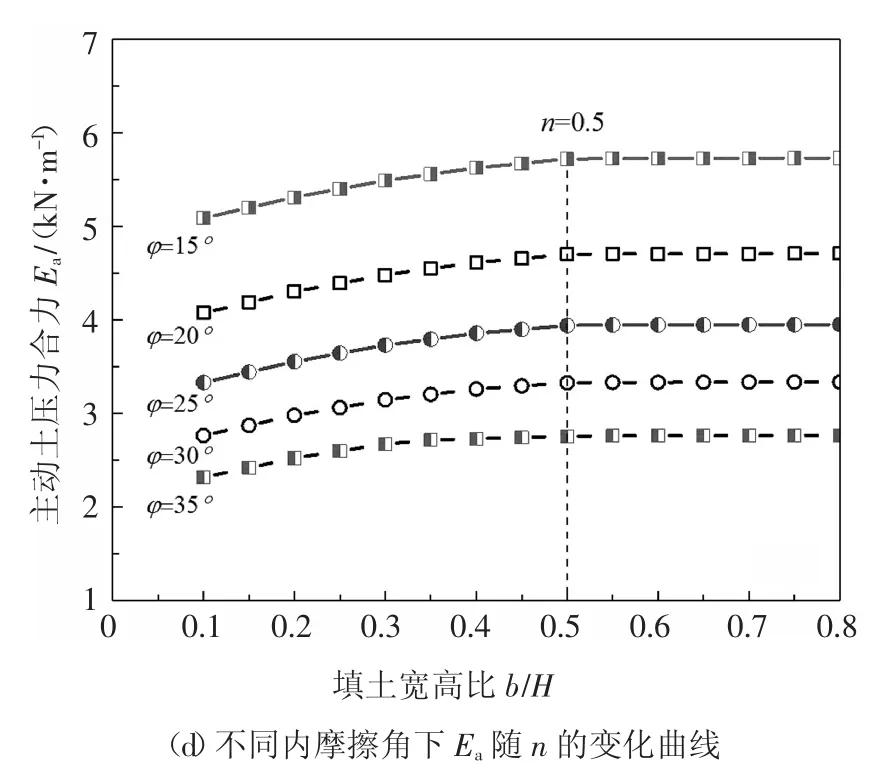
图8 不同参数情况下主动土压力Ea 随n 的变化Fig.8 Variation of active earth pressure Ea with n under different situations

图8 （c）是在不同的墙土摩擦角δ 下主动土压力Ea随着宽高比n 的变化曲线.参数假定为：挡土墙高度H=1.4 m，内摩擦角φ=32.75°，填土重度γ=14.88 kN/m3，墙土摩擦角分别为δ=φ/3、δ=φ/2、δ=φ2/3、δ=φ，宽高比n 的变化范围为0.1～0.8.由图可知，随着墙土摩擦角的增大，主动土压力值显著减小.在不同的墙土摩擦角下，主动土压力值随宽高比的变化均呈先单调递增，后趋于稳定的土压力值.主动土压力值基本保持不变时的宽高比为n=0.5，即为有限宽度临界值.

图8（d）是在不同的内摩擦角φ 下主动土压力Ea随着宽高比n 的变化曲线.参数假定为：挡土墙高度H=1.4 m，墙土摩擦角δ=φ，填土重度γ=14.88 kN/m3，填土内摩擦角分别为φ=15°、20°、25°、30°、35°，宽高比n 的变化范围为0.1～0.8.由图可知，随着内摩擦角的增大，主动土压力值显著减小.在不同内摩擦角下，主动土压力值随宽高比的变化均呈先单调递增，后趋于稳定的土压力值.主动土压力值基本保持不变时的宽高比为n=0.5，即为有限宽度临界值.