带锥形桩帽复合地基桩土应力比计算及其数值模拟
2020-04-11赵明华徐泽宇张承富
赵明华,徐泽宇,张承富
(湖南大学 土木工程学院,湖南 长沙410082)
锥形桩帽桩是相对于等截面桩的一种变截面桩,由于其具有良好的承载传力结构特性,在路堤及车辆荷载作用下, 能够通过倾斜的桩身将其所承受的一部分垂直荷载转换成作用在桩周土上的水平推力,同时也增大了桩侧摩阻力,提高桩的承载能力.锥形桩帽桩锥帽部分的受力特征与锥形桩相似, 国内外学者关于锥形桩开展了一系列研究:何杰等[1-4]研究发现,锥形桩的承载能力高于等截面桩.Ladanyi 和Guichaoua[5]在永久性冻土中分别进行了锥形桩、等截面桩的载荷试验, 研究结果表明锥形桩的承载性状优于等截面桩.Sawaguchi[6]在砂土中进行模型试验研究,试验结果表明锥角能有效减少负摩阻力.刘杰等[7]研究了锥形桩在桩顶施加竖向荷载作用下的极限承载力、桩侧摩阻力及桩端阻力的发展规律.在此基础上,刘杰等[8]采用夯实水泥土锥形桩复合地基加固软土地基,得到了合理的锥角范围.胡向奎等[9]结合实际工程,推导了锥形桩复合地基承载力及沉降计算公式.Dias 等[10]对锥形桩帽桩的施工进行了说明,表明该工艺施工方便,能有效节省时间和钢筋与混凝土的用量,并用数值模拟方法对其与等截面桩进行了对比,对比了不同桩帽大小情况下路堤沉降量和最大弯矩值的差异,但是未对该桩型的作用机理进行研究.
桩土应力比是反映柔性基础下刚性桩复合地基工作状态的重要参数,也是其承载力和沉降计算的重要指标. 国内外众多学者开展了桩土应力比计算方法的研究,刘吉福[11]基于上部路堤内外土柱在剪切应力作用下应力重分布解析模型,建立了桩土应力比公式;陈云敏等[12]考虑了拱顶及拱脚土单元体实际可能的应力状态,对Hewlett 的空间土拱效应分析方法进行了改进,得出了桩体荷载分担比计算公式;朱世哲等[13]假设垫层为理想弹性体和理想弹塑性体两种情况,同时假设桩侧摩阻力均匀分布,推导了刚性桩复合地基桩土应力比计算公式;陈仁朋等[14]建立了考虑土、桩、路堤变形和应力协调的平衡方程,分析了三者协调工作时荷载的传递特性,获得了桩土荷载分担比;曹卫平等[15]基于室内模型试验,对桩承式加筋路堤的桩土应力比变化规律及其影响因素进行了系统的研究;谭慧明等[16]考虑了加筋褥垫层与路堤填土的共同作用,基于小挠度弹性地基板理论,得到了求解等沉面高度、桩土应力、桩土差异沉降的计算公式;吕伟华等[17]针对高速公路中的刚性桩支撑的桩承式路堤,综合考虑路堤中的土拱效应与加固区桩土相互作用,提出了一种桩土应力比的计算方法,其适用于路堤填筑高度较高的情况;赵明华等[18]引入大挠度环形薄板考虑加筋垫层的柔性筏板效应与拉膜效应,假设摩阻力与桩土相对位移呈双曲线关系,建立了路堤、水平加筋体、桩体、桩间土协调变形三维模型,获得了荷载分担比计算方法;杨明辉等[19]将桩网复合地基划分为土工格栅、桩及桩间土单元体,考虑高填方段的土拱效应和薄膜处的荷载分担关系,得到了桩网复合地基桩土应力比计算公式.武崇福等[20]根据垫层、桩、土变形协调方程,将桩侧摩阻力分布由试验曲线简化为线性模式,推导了中性点深度、桩顶平面处桩土应力比. 赵明华等[21]假设桩体向上刺入路堤的体积等于土拱区体积的压缩量,结合变形协调特性,获得了桩土应力比计算公式.
综上可知,尽管前人对桩承式路堤桩土应力比计算、锥形桩复合地基的工作性状等方面做了许多研究,但关于路堤荷载下带锥形桩帽复合地基的研究似尚未见报道. 本文以带锥形桩帽复合地基等效单元为研究对象,根据桩土的沉降差异与上部路堤的荷载转移,考虑带锥形桩帽复合地基桩土相互作用,将复合地基分为路堤填土、加固区及下卧层三部分,并对这三部分进行分析得出路堤荷载下带锥形桩帽复合地基桩土应力比的计算方法. 采用数值模拟对理论计算方法进行验证,同时分析带锥形桩帽复合地基桩土相互作用模式和锥角对路堤沉降以及桩身受力状态的影响,以期为同类工程提供参考.
1 路堤部分计算分析
路堤部分计算参考刘吉福[11]土柱模型,如图1所示,在路堤荷载作用下,由于桩、土压缩模量的差异性,在相同的荷载作用下,桩间土的压缩变形量大于桩顶的变形量,在桩顶平面处产生了沉降差Δ1,即桩间土上部填土相对于桩顶上部填土向下滑移了Δ1.因此内外土柱之间会产生剪应力,外土柱受到向上的剪应力,相反内土柱受到向下的剪应力.外土柱通过剪应力将自身部分荷载转移到了桩顶上部填土中,即太沙基提出的土拱效应.这种变形差异,随着距桩顶高度的增加而减小,当差异变形等于零时,其位置距离桩顶为he,称此高度处平面为等沉面.
桩体上方填土简化为直径为D 的圆柱体,桩间土上方填土简化为以桩体为中轴线的圆筒体,其等效直径为de,de= 1.05l(等边三角形布桩,l 为桩间距)或de=1.128l(正方形布桩)[13].

图1 桩顶填土作用示意图Fig.1 Forces caused by the filling above the pile
取z 轴零点在填土顶面,向下为正.从桩顶上部土柱中深度z 处取dz 厚度的单元进行竖向受力平衡分析可得
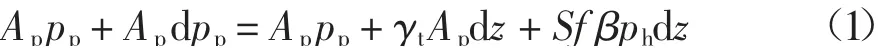
式中:Ap=πD2/4,D 为桩顶处的直径;pp为内土柱在z 处竖向应力;γt为填土容重;S=πD;f=tanφe,φe为外土柱填土的内摩擦角;β 为侧向摩擦力发挥程度系数,与内外土柱间相对位移大小有关,柱顶面为1,等层面处为0,ph为内外土柱z 处的水平应力,ph=kipp,ki为内土柱填土水平土压力系数,刘吉福等[11,14]建议β 取值为1,ki=tan2(45°-φi/2),φi=φe=φ,其中φi为内土柱填土的内摩擦角.因此由式(1)可得
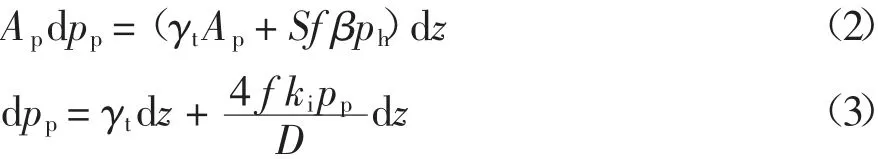
为了保证路面的平整度,通常情况路填土厚度都大于等沉面高度,即h >he.对式(3)采用一阶线性微分方程求解,并引入边界条件:当z=h-he时,pp=γt(h-he),可求得桩顶至等沉面任意截面处的内土柱竖向应力为
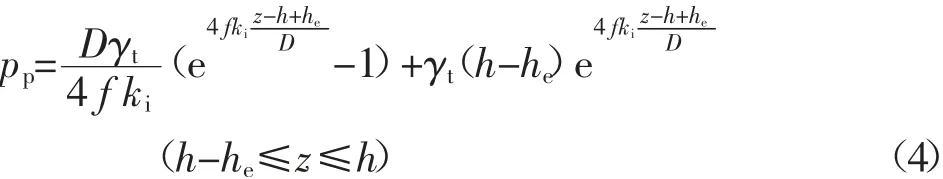
由z 平面处填土竖向受力平衡条件可得

式中:m0=Ap/Ae为置换率(桩顶),Ae=πee2/4 为等效加固面积(桩顶);ps为z 处外土柱的竖向应力.

由式(5)可得联立式(4)、(6)可得

令路堤土的压缩模量为Ec,则桩顶平面处的桩土沉降差为

式(7)、(8)仅有等沉面高度he这个未知数参量,而等沉面高度取决于土拱效应的发挥程度,即与桩土相互协调变形有关.这也是考虑桩承式路堤整体相互协调变形时将路堤与桩-土加固区连接的变形、应力连续条件.
2 加固区的计算分析
加固区如图2 所示,图中L0为桩帽高度,L1为中性点位置,Lp为桩长,re为等效半径,r1为桩帽顶半径,r2为桩帽底半径,α 为锥角. 以桩顶为z 轴零点,向下为正,加固区分三部分进行计算分析,z=0 ~L0为桩帽区;z=L0~L1为负摩阻力区;z=L1~Lp为正摩阻力区.

图2 加固区示意图Fig.2 Schematic diagram of reinforcement area
2.1 桩帽区
桩帽区桩土接触面受力状态如图3 所示,其受力状态在后文数值结果中得到了验证.
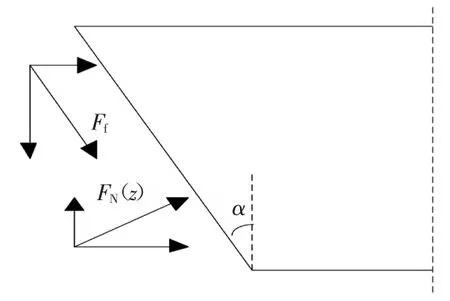
图3 桩土接触面受力状态Fig.3 The stress state of the pile-soil interface
桩帽区根据桩土相互作用分析可得
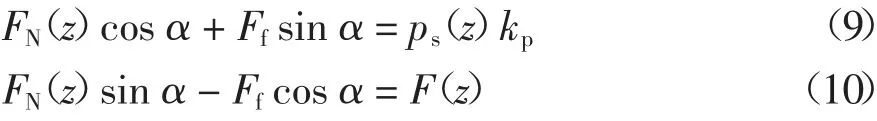
式中:ps(z)为z 深度处桩周土竖向应力,FN(z)为桩周土对桩体的法向压力,F(z)为桩周土对桩的竖向应力分量,Ff=FN(z)tanφsp,φsp为桩土接触面处的内摩擦角φsp=0.8φs[22],kp=tan2(45°+φs/2)为被动土压力系数,φs为桩周土内摩擦角.
联立(9)、(10)两式可得

式中:c=cosα+tanφspsinα,s=sinα-tanφspcosα.
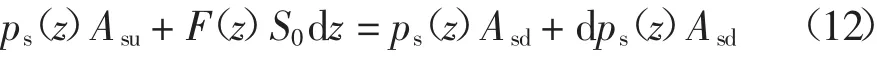
如图2,桩帽部分桩间土薄单元竖向受力满足如下平衡关系式中:Asu为桩间土薄单元顶部面积,Asd为桩间土薄单元底部面积,取Asu=Asd=π(re2-(r1-kz)2),S0=2π(r1-kz)为薄单元桩土接触位置周长(桩帽区),此处k=tanα.将边界条件z=0 时,即桩帽顶位置处,ps(z)=ps(0)代入式(12)求解微分方程,可得
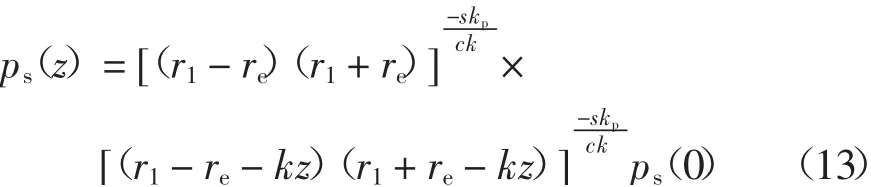
又因在z 深度处满足
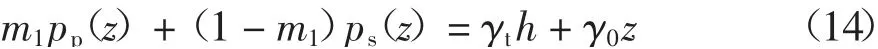
式中:m1=π(r1-kz)2/πre2为z 深度处置换率(桩帽区),γ0为土的重度(桩帽区).
联立式(13)、(14)可得
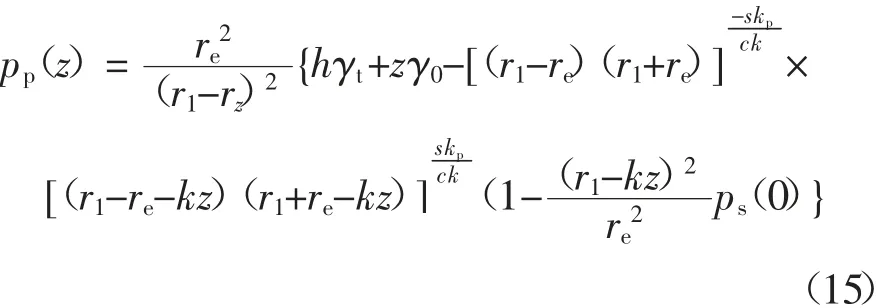
通过式(13)、(15)可得桩帽区桩间土压缩量Ss1和桩体压缩量Sp1

式中:Es1、Ep分别为桩帽区土体压缩模量和桩体压缩模量.
2.2 负摩阻力区
z=L0~L1区间桩土间相互作用摩阻力分布形式参考董必昌等[23]采用的Berrum 公式计算桩侧摩阻力,其分布为

式中:ka=tan2(45°-φs/2),为主动土压力系数,μ1、μ2分别为负、正桩侧摩阻力发挥系数,其取值参考文献[24].
负摩阻力区的桩间土薄单元竖向受力满足如下平衡关系
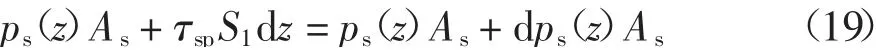
式中:As=π(re2-r22)为桩间土薄单元上下面面积(正、负摩阻力区),S1为薄单元桩土接触位置周长(正负摩阻力区).在z=L0处可由式(13)得ps(L0),作为边界条件代入式(19)可得
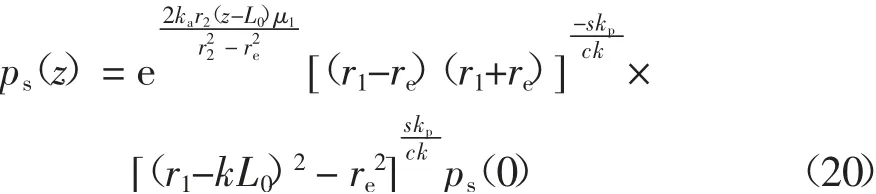
又因在z 深度处满足
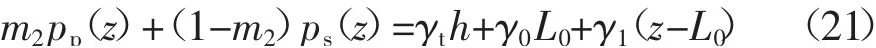
式中:m2=πr22/πre2为置换率(正负摩阻力区),γ1为土的重度(正负摩阻力区),可得
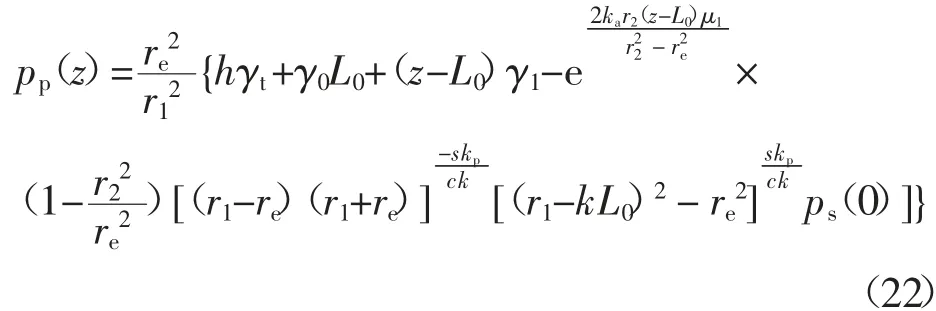
通过式(20)、(22)可得负摩阻力区桩间土压缩量Ss2和桩体压缩量Sp2

式中:Es2、Ep分别为负摩阻力区、正摩阻力区土体压缩模量.
2.3 正摩阻力区
z=L1~Lp区间桩土间相互作用摩阻力分布形式参考董必昌等[23]采用的Berrum 公式计算桩侧摩阻力,其分布为

正摩阻力区的桩间土薄单元竖向受力满足如下平衡关系

在z=L1处可由式(20)得ps(L1),作为边界条件代入式(26)可得
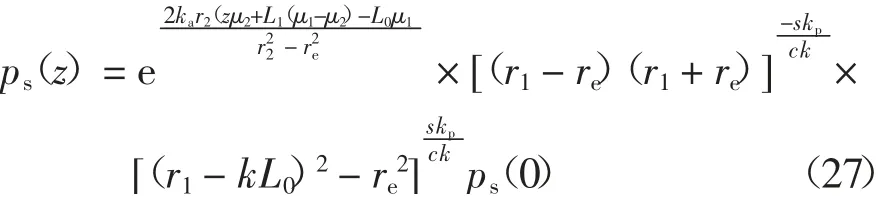
同2.2 节分析,可得

通过式(27)、(28)可得负摩阻力区桩间土压缩量Ss3和桩体压缩量Sp3

3 下卧层的计算分析
假定下卧土层符合Winkler 地基模型,令桩端刺入量为Δ2,可知
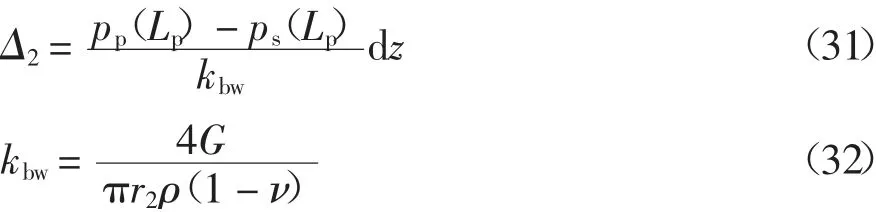
式中:kbw为桩端下卧层地基土层刚度系数[24],G 为土的剪切模量,ν 为泊松比,ρ 为桩端影响深度系数,Randolph 等[24]建议取0.85.
综上所述,桩土相对位移在桩顶处与桩底处分别达到正负位移的最大值.根据连续性条件,在桩顶平面处路堤填土的内外土柱的最大相对位移等于桩土相对位移的最大负值;在桩底平面处,桩土的相对位移达到最大正值且等于桩向下刺入下卧层的位移,可得

Giround 等[25]指出当φs>20°时可取katanφs=0.25.假设桩的几何参数,桩、土基本力学参数和各系数已确定的情况下,可按图4 所示流程图进行计算.
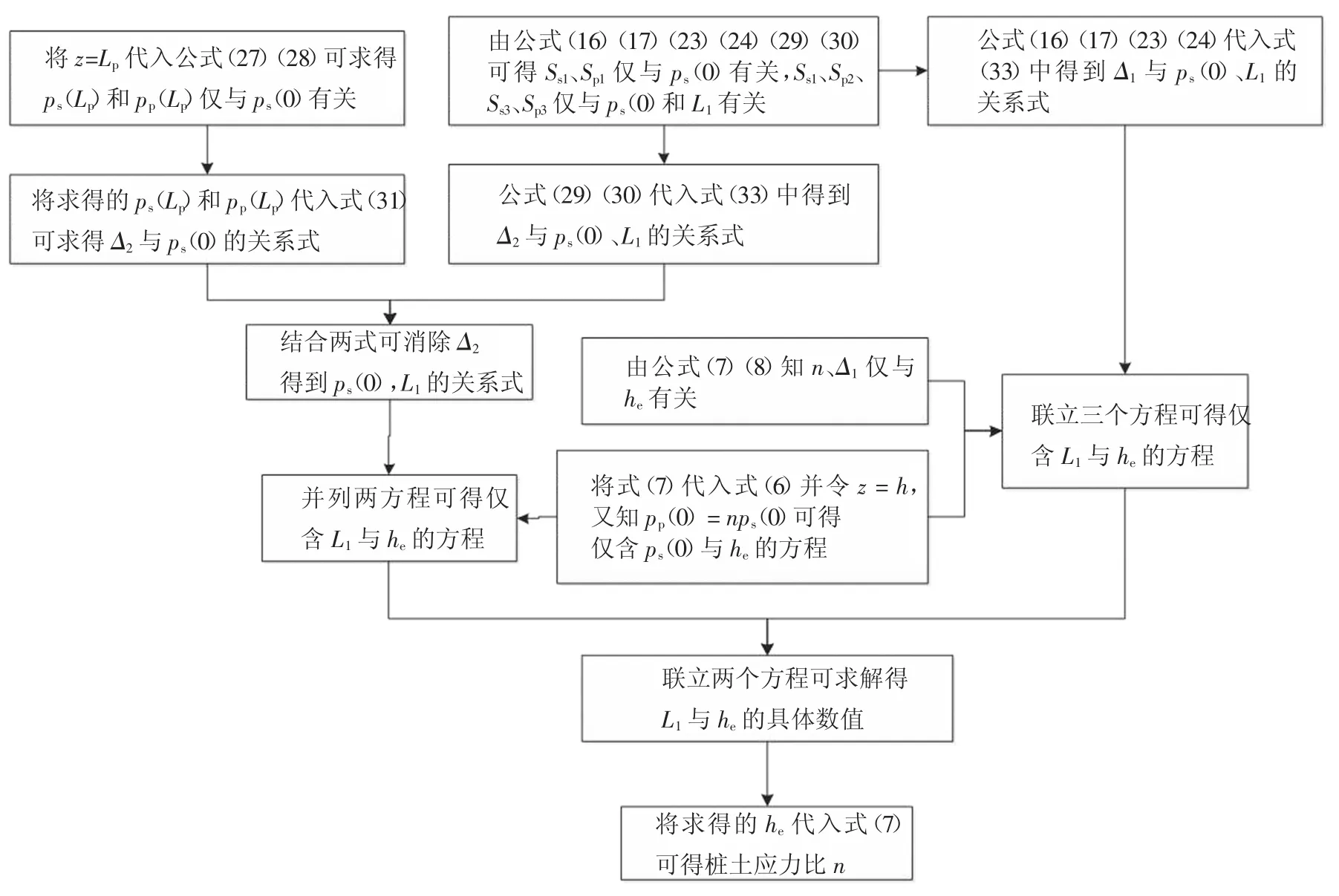
图4 计算流程图Fig.4 Calculation flow diagram
4 数值模拟
4.1 模拟方案
数值模拟采用有限差分软件FLAC3D,土体采用Mohr-Coulomb 模型,桩体采用线弹性模型,桩土之间的接触面参数有法向刚度kn、剪切刚度ks、黏聚力c、内摩擦角φ,其中kn、ks可以取接触面相邻区域“最硬”土层的等效刚度的10 倍[22],即公式(34)所示,c、φ 值取0.8 倍土层相应的黏聚力和摩擦角.计算参数见表1,取自文献[14].
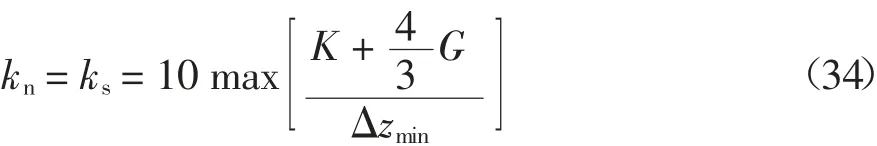
式中:K 为体积模量,G 为剪切模量,Δzmin为接触面法向方向上连接区域最小尺寸.

表1 计算参数Tab.1 Calculation parameters
利用模型的轴对称性,取单位厚度为1 进行分析,模型边界取桩有效影响半径re=1.2 m.地基土自上而下分3 层,第一层为工作平台,厚度2 m,是施工前为承载施工机械对地基土作的预处理,该层层厚为桩帽高度L0=2 m.第二层为软土层,厚度10 m.第三层为下卧硬土层,厚度6 m,模拟时桩正好打穿软土层即桩长Lp=12 m.模型边界施加相应的约束,即模型表面自由,前、后、左、右四个边界面添加水平法向约束,底面边界添加水平、竖向约束.数值模拟过程分为两步:桩和地基的自重应力平衡;施加路堤后达到平衡. 本文获取的是施加路堤达到平衡后的数据结果.
模拟目的是为研究锥形桩帽桩在路堤荷载下桩土相互作用与等截面桩、常规带帽桩(桩帽高度为0.3 m)的差异,不同锥角对复合地基性状的影响,其中锥角用桩径比D/d(桩帽顶直径/桩帽底直径)来控制.对比方案见表2.图5(a)(b)(c)分别为带锥形桩帽复合地基、等截面桩复合地基和常规带帽桩复合地基的模型图及其桩土接触面.
表2 对比方案Tab.2 Comparison program

图5 计算模型及其桩土接触面Fig.5 Computational model and pile-soil interface
4.2 桩土应力比与路堤沉降
图6 给出了桩土应力比随着锥角的变化关系图.图6 的对比结果表明:随着D/d 从2 增大到3.5,即锥角从5.7°增大到14°,数值模拟的桩土应力比值从3.06 减小到2.08,而公式计算值从3.13 减小到2.19,桩土应力比的计算值与模拟值的变化趋势一致且值很接近,相对误差在2.01%~6.44%范围内.随着锥角变大,桩帽顶的宽度相应增加,有更多的荷载传递到桩顶.图6 显示桩土应力比随着锥角增大而减小,这是因为桩帽宽度D 增大后,虽然有更大的路堤荷载传递到桩帽上,但桩帽的尺寸相对增加得更大,故其所承担的应力值反而减小了.计算值稍大于模拟值,这可能是因为第一节路堤计算分析时,假设侧摩阻力发挥程度系数为1,而该系数在桩顶面处为1,在等沉面处为0.
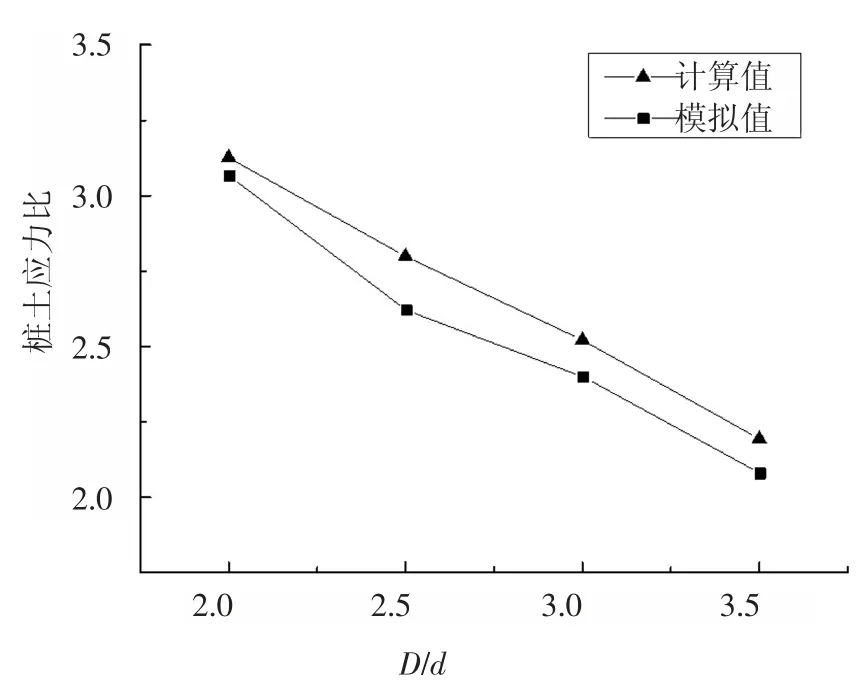
图6 桩土应力比与锥角的关系Fig.6 Relation between pile-soil stress and taper angle
图7 表示了路堤表面沉降与桩顶直径D 的关系,带锥形桩帽复合地基路堤表面沉降随D 的增大呈线性减小. 等截面桩复合地基和常规带帽桩复合地基在D 值较小时,D 的增大对其沉降控制有明显的效果,当D 较大时,沉降控制效果不再增加.对比各桩型的沉降控制效果,需保证桩顶净距相同,故对比了桩顶直径D 相等时的路堤表面沉降,见图7,带锥形桩帽复合地基控制路堤沉降的效果较等截面桩、常规带帽桩好.锥形桩帽桩与等截面桩相比,D=0.6 m 和D=1.4 m 时,后者沉降值较前者分别大0.84%和8.91%.锥形桩帽桩与常规带帽桩相比,D=0.6 m 和D=1.4 m 时,后者沉降值较前者大2.0%和8.3%.
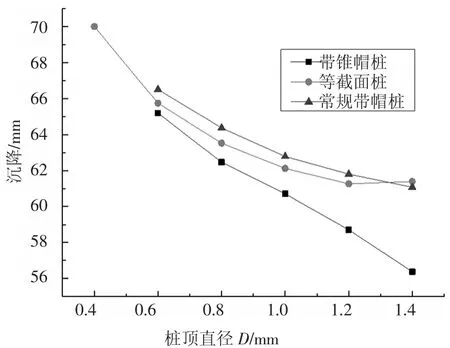
图7 路堤表面沉降值与桩顶直径的关系Fig.7 Relation between the settlement and diameter of the pile head for the embankment surface
4.3 路堤荷载下桩土相互作用
下面以桩身轴力、土对桩的竖向应力分量、桩帽处桩土相对位移来分析路堤荷载下带锥形桩帽复合地基的桩土相互作用.
图8 所示为桩身轴力曲线,为了使图像清晰,仅选取等截面桩D=0.4 m 和D=0.6 m 进行对照. 由图可见等截面桩轴力在桩身很大范围内随深度增加而增大,由于设计时需按照最大轴力处设计截面尺寸,而等截面桩桩身截面积不变,故在小轴力截面位置处材料花费较多,造成工程浪费.对于锥形桩帽桩,桩帽部位轴力很大,且锥角越大对应的桩帽顶部轴力越大;桩身轴力随着深度增加逐渐减小,同时锥帽尺寸也相应减小;桩帽以下部位,桩身轴力较等截面桩小了约1~2 倍,轴力沿桩身分布比较均匀,满足轴力越大的位置,材料使用越多的原则,能有效地节省费用.
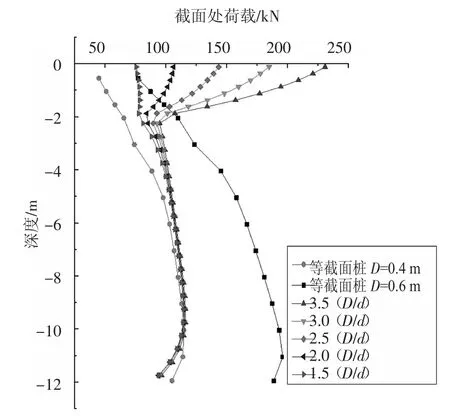
图8 桩身轴力曲线Fig.8 Curves of axial force on column
同时可以发现,当锥形桩帽桩D/d=1.5 时,桩帽处的轴力随深度基本不发生变化,说明桩土竖向相互作用为零,但并不意味着桩土之间没有力的作用.后文中对其进行了解释,是因为存在临界锥角,两个竖向分力发生了抵消.
对桩顶处轴力进行分析可得,当锥形桩帽桩D/d=1.5,即桩帽顶直径与等截面桩顶直径相等(0.6 m)时,桩顶处轴力很接近(为76 kN).桩帽D/d 的值越大,其桩顶处轴力越大.即桩顶面积越大,桩体所分担的路堤荷载就越多,土拱效应发挥越充分.
锥形桩帽桩轴力与等截面桩轴力的最主要差异是:前者在桩帽部分随深度而减小,说明桩帽受到了桩间土对其向上的作用力,桩帽以下部分桩身轴力变化趋势与等截面桩一致,由此我们主要对桩帽处的桩土相互作用作进一步的研究.
图9 所示为土对桩的竖向应力分量沿桩身的曲线图,可以看出锥形桩帽桩锥角较小(D/d=1.5)时,在桩的上部,土对桩的竖向应力分量为负值.当锥角变大时,土对桩的竖向应力分量为正值,这是因为土对桩的竖向应力分量由两部分组成,土对桩沿接触面向下的摩擦力和土对桩垂直接触面向上的法向压力,前者随锥角的增大而减小,后者随锥角的增大而增大,故存在一个临界锥角,控制桩帽处土对桩竖向应力的方向,锥角越大,土对桩向上的应力越大.桩帽下方部位由于不存在锥角,土对桩仅作用沿接触面方向的摩擦力,故土对桩的竖向应力分量急剧减小.
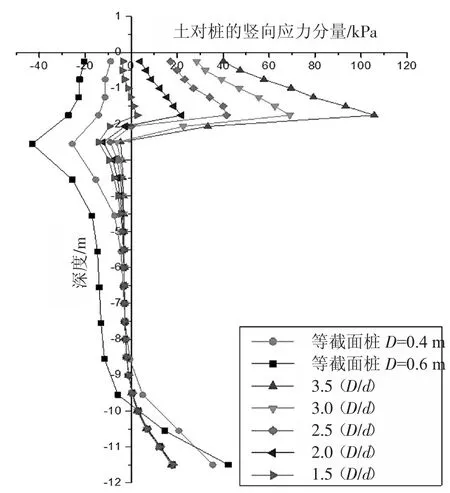
图9 土对桩的竖向应力分量曲线Fig.9 Vertical stress component curve of soil to pile
为了进一步对比带锥帽桩与等截面桩,建立了与带锥帽桩相同桩身截面积的等截面桩复合地基模型(D =0.4 m).由图8 可得,D =0.4 m 的等截面桩,桩顶所承受的荷载较小,故大部分荷载由桩间土承担,通过监测得到D=0.4 m 时的桩间土平均应力值为74.8 kPa 大于D = 0.6 m 时桩间土平均应力值68.9 kPa,将产生较大的桩间土沉降,这主要是由于置换率较小.由图7 可知,其路堤沉降达到了70 mm.
土对桩的竖向应力分量对于等截面桩,其值等于桩土之间的摩阻力;对于带锥帽桩,由于锥帽处受到桩土之间的法向应力,故仅在锥帽以下深度范围内的值等于桩土之间的摩阻力. 可以看出变截面桩在桩帽以下部分的负摩阻力与等截面桩相比减小了很多,反映了锥角能有效减小负摩阻力对基桩的影响,充分发挥桩体的承载能力,这与Sawaguchi[6]针对砂土中锥形桩的模型试验研究结论一致. 等截面桩中性点位置在-11 m 深度附近,锥形桩帽桩在-9 m深层附近,故锥形桩帽桩能提高中性点的位置,充分发挥桩身正摩阻力,提高承载力.为判断桩土相对位移方向,用FLAC3D 软件中plane 命令对模型在桩帽顶以下-1 m 深度处进行了水平方向的切片,见图10.水平、竖直位移切片云图见图11.由此可知桩土相对位移方向,即当土沉降比桩要快时,土将从桩的表面脱离,且上部土将向桩侧补充,从而对桩产生挤压力和摩擦力,其桩土相对运动趋势见图12(a),相对于刚性基础下桩帽部分桩土相对位移见图12(b)[26],路堤荷载下桩帽部分桩间土对桩的摩擦力是沿着锥面向下. 图中P,P′分别表示为加载前后桩内某点的位置;S,S′分别表示加载前后桩周土某点的位置.Vp,Vs分别表示桩、桩周土的竖向位移;Us表示桩周土的水平位移.
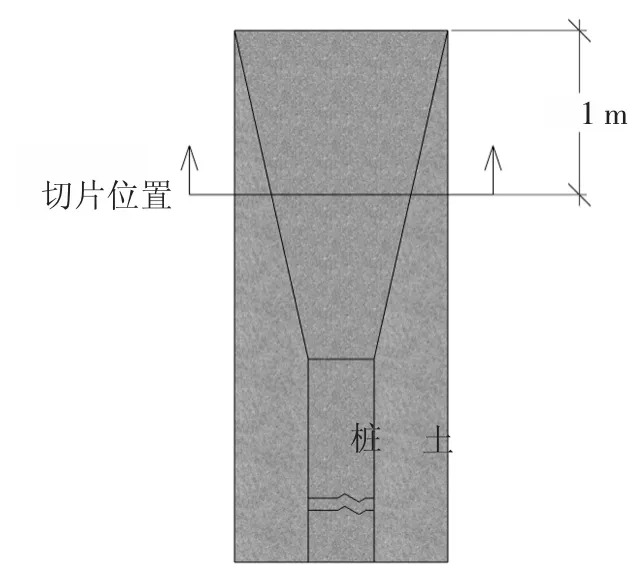
图10 切片位置示意图Fig.10 Schematic diagram of slice position

图11 距桩顶-1 m 处模型切片云图Fig.11 Model slice contour at-1 m from pile top
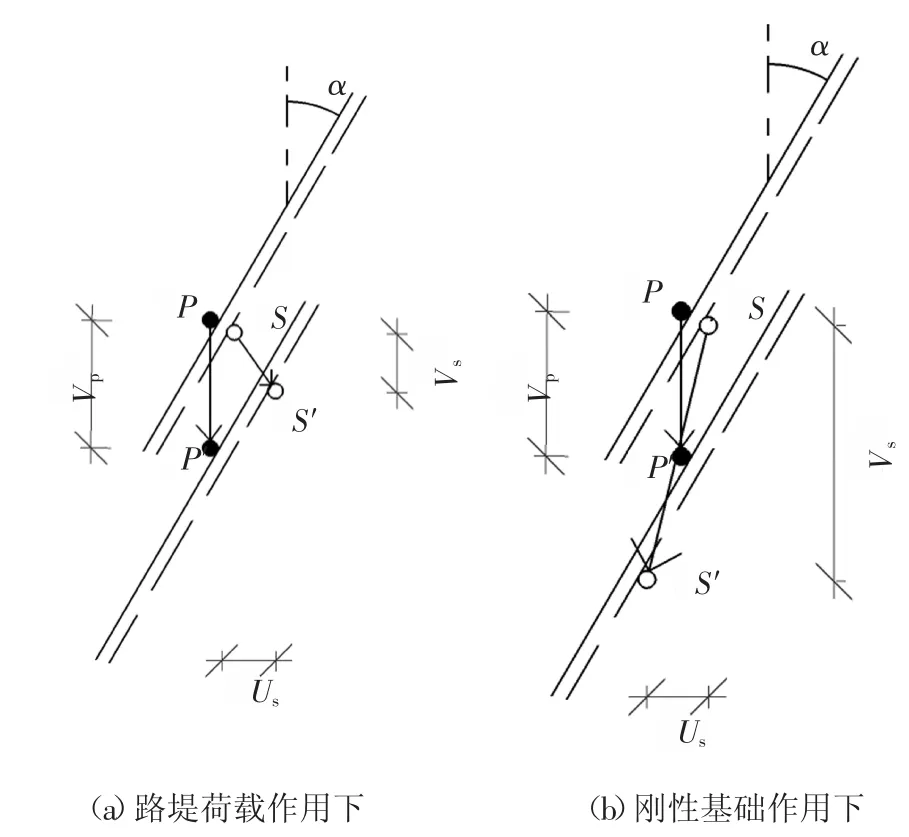
图12 桩土相对位移Fig.12 Relative displacement of pile and soil
5 结 论
本文根据路堤-桩-土相互作用协调变形的特点,考虑桩土的刺入模型,推导了路堤荷载下带锥形桩帽复合地基的桩土应力比公式. 并采用FLAC3D数值模拟分析了路堤荷载下带锥形桩帽复合地基的桩土相互作用及锥角大小对桩土应力比和路堤沉降的影响,主要得出以下结论:
1)锥形桩帽桩能改善桩身的受力状态,使截面积大的部位轴力大,截面积小的部位轴力小,充分发挥桩体强度;锥角的存在能有效减少负摩阻力对桩的影响,充分发挥桩体的承载能力.
2)锥形桩帽能够通过倾斜的桩帽将其所承受的部分竖向荷载传递到桩周土体中,存在一个临界锥角,控制桩帽处土对桩竖向应力的方向,锥角越大,土对桩向上的应力越大.
3)当土沉降比桩要快时,土将从桩的表面脱离,上部土会向桩侧补充,避免了“塌空区”,验证了锥形桩帽处桩土相互作用模式:桩周土对桩产生垂直于桩土表面向上的挤压力和平行于桩土表面向下的摩擦力.
