TC4-DT焊接接头I-II复合型疲劳裂纹扩展实验及模拟研究

2020-04-11刘小刚朱笑林郭海丁

航空材料学报 2020年2期

刘小刚,朱笑林,郭海丁

（南京航空航天大学能源与动力学院江苏省航空动力系统重点实验室，南京 210016）

TC4-DT是一种损伤容限型钛合金[1]，与传统的钛合金相比具有更高的韧性和更低的裂纹扩展速率[2]，因其具备较好的塑性、韧性和良好的焊接性能及较长的使用寿命，正越来越广泛应用于航空航天领域。此外，电子束焊接技术[3]也将成为航空发动机钛合金整体部件制造的关键技术。发动机转子部件常常采用焊接结构来减轻重量，如压气机盘轴等，其焊接部位往往承受离心力、轴向力、扭矩等多种载荷的共同作用，一旦出现裂纹，则呈复杂的复合型裂纹扩展模式。目前的研究多局限于Ⅰ、Ⅱ、Ⅲ型裂纹[4]单独扩展的情况，当预测复合型裂纹扩展行为和剩余寿命评估的时候，会产生较大误差。因此开展复合型疲劳裂纹扩展研究对于此类构件的寿命评估具有重要意义。

目前已有研究者对钛合金焊接接头疲劳裂纹扩展开展了相关研究，Muzvidziwa等[5]通过实验研究Ti-6Al-4V摩擦焊焊接接头的裂纹扩展行为，得到焊接接头不同区域的裂纹扩展速率。Balasubramanian等[6]对Ti-6Al-4V钨极脉冲氩弧焊接、激光束焊接和电子束焊接三种不同焊接接头的裂纹扩展行为进行了研究，认为焊缝的疲劳裂纹扩展行为与焊缝的力学性能和焊缝区域的微观组织特征有关。Jinkeun等[7]研究Ti-6Al-4V钛合金氩弧焊和电子束焊接头各区性能与组织的关系及接头疲劳裂纹扩展速率在各区的变化与组织的关系。对于Ⅰ-Ⅱ复合型疲劳裂纹，Doquet等[8]对带有中心预制裂纹的Z2NKD-18-8-5马氏体钢进行复合型疲劳裂纹扩展实验，发现加载路径对复合型裂纹扩展路径有很大影响。Sander等[9]采用CTS试样开展Ⅰ-Ⅱ复合型疲劳裂纹扩展实验，研究加载方向对裂纹扩展行为的影响。Ma等[10]采用 CTS试样研究加载角度对Ⅰ-Ⅱ复合型疲劳裂纹扩展速率的影响。Ding等[11]采用1070钢的圆形紧凑试样研究加载方向对Ⅰ-Ⅱ复合型疲劳裂纹扩展行为的影响，发现加载方向改变，裂纹扩展路径会瞬时急剧转变，而后转变到与外载近似垂直的方向。

综合来看，对于钛合金焊接接头的裂纹扩展研究主要集中在不同区域组织对扩展行为的影响，或仅针对拉伸载荷下疲劳裂纹扩展速率的研究，而对于Ⅰ-Ⅱ复合型疲劳裂纹扩展的研究较少。本工作拟对TC4-DT钛合金电子束焊接头Ⅰ-Ⅱ复合型疲劳裂纹扩展性能进行研究，通过开展复合型疲劳裂纹扩展实验获得接头拉剪复合载荷下的疲劳裂纹扩展曲线，并采用XFEM对实验过程进行数值模拟计算，分析加载角度对于Ⅰ-Ⅱ复合型疲劳裂纹扩展路径及剩余寿命的影响。

1 TC4-DT 电子束焊接头Ⅰ-Ⅱ复合型疲劳裂纹扩展实验

1.1 试件及夹具

实验材料为TC4-DT钛合金，采用电子束焊接工艺将两块板件对接焊到一起，焊接工艺参数如表1所示，焊后经600 ℃保温4 h工艺热处理，随炉冷却以消除残余应力。

表1 TC4-DT 焊接接头焊接工艺Table 1 Welding procedure of TC4-DT welded joint

TC4-DT电子束焊对接接头为高强匹配接头，母材（base metal，BM）及焊缝（welded metal，WM）区域基本材料参数[15]如表2所示。

表2 TC4-DT 焊接接头基本力学性能参数Table 2 Basic mechanical properties of TC4-DT welded joint

根据加工的TC4-DT电子束焊接头板件设计紧凑拉伸剪切（compact tension-shear，CTS）试样，其几何尺寸如图1（a）所示。切口及初始预制裂纹位于试件中间的焊缝区，如图中阴影部分所示，焊缝宽度为 5 mm。总长度为试样宽度的一半（30 mm），其中切口长度为 28.5 mm，剩余 1.5 mm的预制裂纹通过线切割的方式加工而成。在上下端各加工出3个直径为8 mm的螺栓孔，便于与夹具的连接固定。采用Richard[12]设计的夹具进行装夹和加载，如图1（b）所示。此装置通过外部的七对加载孔与夹持端相连接，可以实现每隔15°不同方向的加载，加载角度定义为远场拉应力与裂纹平面法线方向的夹角（如图1（c）所示）， α =0◦为纯Ⅰ 型加载， α =90◦为纯Ⅱ 型加载， 0◦<α<90◦时为Ⅰ-Ⅱ复合型加载。

整个加载装置可以实现由平面纯拉伸到平面拉伸/剪切到平面纯剪切等不同加载角度的加载，可以分析不同拉剪比例下的复合型裂纹扩展。

1.2 实验方案

实验在MTS370疲劳试验机上进行，实验条件为室温，使用电子显微镜来追踪裂纹扩展，每隔一段时间，记录相应的循环周次以及裂纹长度，并观察裂纹前缘的形貌及裂纹扩展路径。采用正弦波加载，最大载荷为 20 kN，应力比 0.1，频率 10 Hz。加载角度α= 0°、30°、60°、90°（图 2），每种实验条件重复2到3次。

图1 CTS试样及夹具（a）试样设计尺寸；（b）试样与夹具装配图；（c）加载角度示意图Fig. 1 CTS specimen and loading device （a）dimensions of specimen；（b）assembly of specimen and its loading device；（c）loading angles of specimen

图2 不同角度裂纹扩展实验加载方式Fig. 2 Loading modes of crack growth test at different angles （a）；（b）；（c）；（d）

1.3 结果及分析

1.3.1 复合型疲劳裂纹开裂角

4种不同加载角度下的复合型裂纹典型扩展形貌如图3所示。由图3可知，随着加载角度的增大，开裂角逐渐增大。这是因为，在 α =0◦时，裂纹为纯Ⅰ型裂纹，裂纹尖端只承受正应力作用，故开裂角为，随着加载角度的增加，裂纹尖端所受剪切应力增大，裂纹发展为Ⅰ-Ⅱ复合型裂纹，滑开型裂纹的影响逐渐增大，故开裂角逐渐增大。当时，裂纹为纯Ⅱ型裂纹。

图3 复合型疲劳裂纹扩展扩展形貌Fig. 3 Mixed-mode fatigue crack growth topographies （a）α=0°；（b）α=60°；（c）α=60°；（d）α=90°

预制裂纹位于焊缝区，焊缝具有一定的宽度且焊缝与母材的交界线与预制裂纹方向基本平行，裂纹沿一定角度开裂后在焊缝区域扩展一定距离后会达到焊缝与母材的交界处，此时裂纹扩展方向将发生一定角度偏转。以为例进行说明，如图4所示。裂纹沿着开裂角θ1的方向沿焊缝扩展至界面处，裂纹扩展方向发生偏转，沿着与原裂纹面角度为θ2的方向顺着母材继续扩展，交界面处裂纹扩展路径的偏折体现了电子束焊接头非均质性对于裂纹扩展路径的影响。在其余加载角度下也有同样的现象。

表3给出在不同加载角度下裂纹在TC4-DT电子束焊接头焊缝区域的开裂角。开裂角定义为预制裂纹方向与裂纹开裂方向的夹角。表中的理论解分别采用最大周向因子准则和能量密度因子理论来确定。最大周向因子准则认为裂纹初始扩展方向是裂纹尖端最大周向应力方向，并且裂纹发生扩展的条件是裂纹尖端的最大周向应力达到材料破坏的临界值。周向应力的表达式如式（1）：

图4 焊缝与母材界面处裂纹扩展路径偏折（α = 30°）Fig. 4 Deflection of crack propagation path at the interface between weld and base metal（α = 30°）

表3 复合型疲劳裂纹扩展开裂角理论解与实验结果对比Table 3 Comparison of theoretical solution and experimental result of mixed-mode fatigue crack growth cracking angle

式中：σθ为周向应力；r为距离裂尖的距离；KⅠ、KⅡ分别为裂尖Ⅰ型、Ⅱ型应力强度因子。

能量密度因子准则认为裂纹会沿着裂纹尖端应变能密度最小的方向开裂，裂纹尖端的应变能密度因子可写为式（3）：

本实验试样厚度为11.5 mm且裂纹位于试样中间，并在整个范围内，认为裂纹尖端处于平面应变状态。在使用两种开裂角预测理论时，裂尖应力强度因子、通过有限元计算得到。

由表3可知，两种开裂角预测理论的结果均与实验结果存在一定的误差，当加载角度较小，即裂纹偏向于Ⅰ型裂纹时，能量密度因子理论的开裂角预测结果误差较小；当加载角度较大，即裂纹偏向于Ⅱ型裂纹时，最大周向应力准则的开裂角预测误差较小。最大周向应力准则与能量密度因子准则均基于裂尖小范围屈服的线弹性断裂力学的基本假设，且仅适用于均质材料，而焊接接头本身具有非均质的特点，因此使用这两种理论预测时均存在一定误差。本研究的电子束焊接头焊缝区域具有一定宽度，裂纹预制于焊缝中间，在小范围内可以近似认为裂纹尖端处于均质材料中。因此两种理论的开裂角预测误差仍在可接受范围内。

1.3.2 复合型疲劳裂纹扩展速率

实验得到的不同加载角度下裂纹长度随循环数变化曲线如图5所示。由图5可见，在相同载荷作用下，随着加载角度增加，拉伸应力的比例减小，临界裂纹尺寸增大，裂纹扩展寿命提高。

图5 不同加载角度下 a-N 曲线Fig. 5 a-N curves at different loading angles

为了研究复合型疲劳裂纹扩展速率，引入等效应力强度因子Keff[13]的概念来进行分析。在只考虑Ⅰ型裂纹和Ⅱ型裂纹的情况下，Keff可以写成式（6）：

根据Paris公式，用裂纹扩展速率 da/dN与等效应力强度因子幅值Keff的关系曲线来反应复合型疲劳裂纹扩展的规律。

根据载荷大小及裂纹长度，通过有限元计算分别得到加载角度 α = 0°、30°、60°、90°条件下裂纹尖端应力强度因子KⅠ、KⅡ，再将其代入式（6）转化为等效应力强度因子Keff，不同加载角度下ΔKeff随裂纹长度的变化如图6所示。

图6 不同加载角度下等效应力强度因子Fig. 6 Equivalent stress intensity factors at different loading angles

由图6可见，随着加载角度的增大，应力强度因子幅值的增长速率减缓，这是因为不同加载角度裂纹开裂后的开裂角不同，导致在裂纹扩展过程中实际的有效承载面积不同。随着加载角度的增大，有效承载面积增大，裂纹尖端的等效应力强度因子也降低。

等效应力强度因子综合考虑Ⅰ型应力强度因子和Ⅱ型应力强度因子在裂纹扩展中的作用，复合型裂纹扩展速率方程可由Paris公式表示：

由实验得到的 a-N曲线，根据GB 9447—1988，使用割线法计算裂纹扩展速率，使用a-N曲线中两个相邻的数据点直线斜率来计算，其计算公式可以表达为式（8）：

式（8）计算的扩展速率为裂纹长度增量ai+1–ai的平均速率，故计算时ΔKeff采用平均裂纹长度，如式（9）：

不同加载角度及裂纹长度下的应力强度因子分量KⅠ、KⅡ通过有限元计算得到。

不同加载角度双对数坐标系下使用等效应力强度因子幅值对裂纹扩展速率的拟合结果如图7所示。

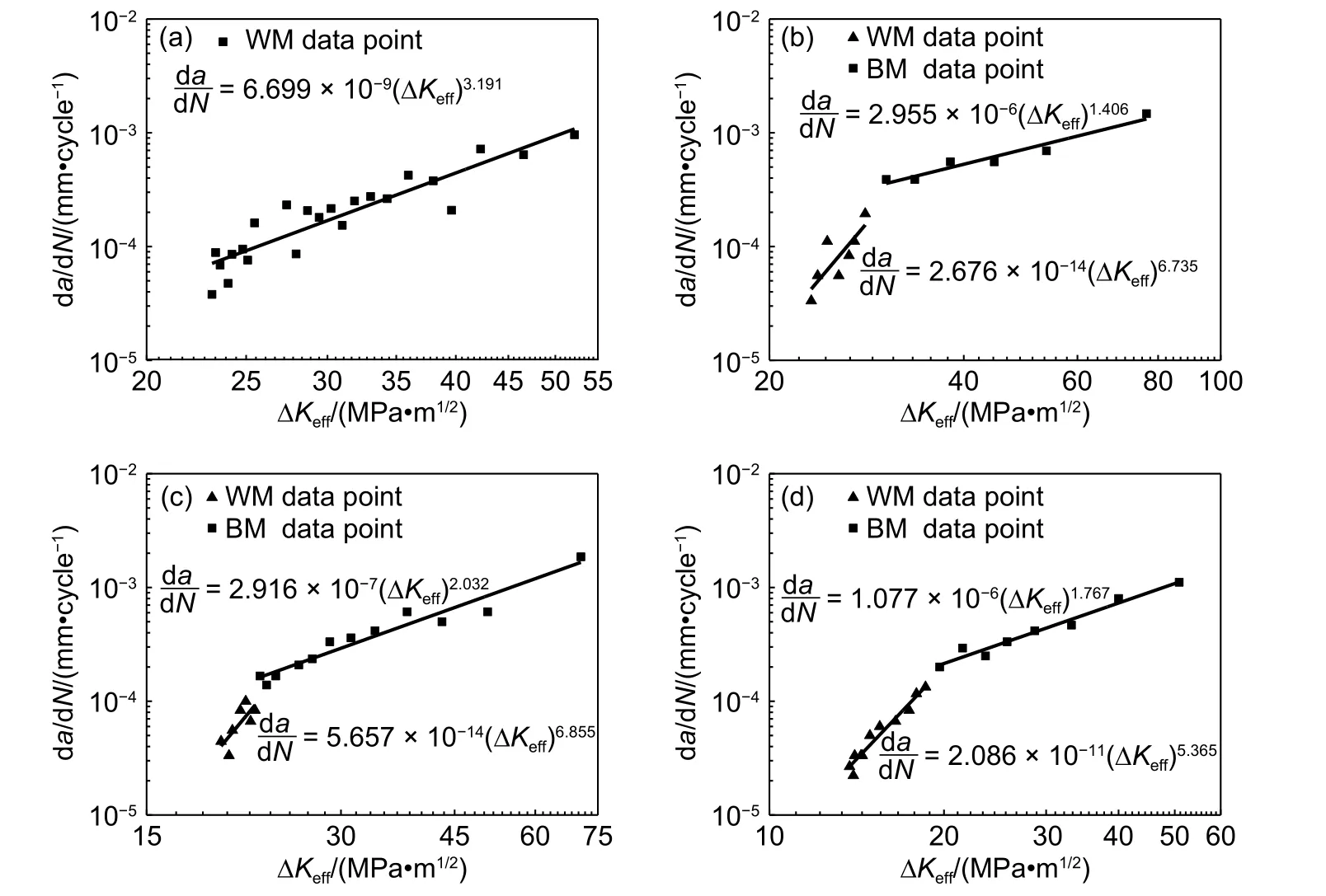
图7 疲劳裂纹扩展速率拟合结果Fig. 7 Fatigue crack growth rate fitting results （a）；（b）；（c）；（d）

2 基于 ABAQUS 的扩展有限元法（XFEM）疲劳裂纹扩展模拟

扩展有限元法（extended finite element method，XFEM）的基本思想于1999年由Belytschko[14]的研究团队首次提出。XFEM与常规有限元法相比，最根本的区别在于它在划分网格时不必考虑结构内部的几何或物理界面。XFEM通过添加加强形函数以解决单元内部的间断性并采用水平集法来追踪裂纹位置，裂纹可以贯穿网格单元，从而在不重画网格的情况下模拟裂纹扩展，使得对裂纹扩展的模拟更加精确，同时降低了模拟裂纹扩展过程的成本，大大提高了计算效率。

2.1 基于 ABAQUS 的 XFEM 疲劳裂纹扩展模拟方法

ABAQUS中基于线弹性断裂力学的扩展有限元法，在进行低周疲劳的分析时主要依据Paris公式来计算疲劳裂纹的起裂和扩展。将Paris公式中的应力强度因子幅值用能量释放率幅值来代替。单元中裂尖附近的能量释放率由虚拟裂纹闭合技术计算所得，疲劳裂纹扩展速率随能量释放率变化的曲线如图8所示。

图8 疲劳裂纹扩展速率与能量释放率G关系曲线Fig. 8 Relationship between fatigue crack growth rate and energy release rate G

图8 中，Gth是能量释放率门槛值，与应力强度因子门槛值ΔGth相对应。Gpl是能量释放率的上限值，Gc是等效应变能释放率的临界值。

疲劳裂纹发生扩展的条件是：

式中：c1、c2为材料常数；为能量释放率幅值。

当能量释放率G < Gth时，裂纹扩展速率为零，裂纹不发生扩展；当满足最大能量释放率Gth Gc时，裂纹扩展将不必经历循环加载。

在线弹性范围内，应变能释放率与应力强度因子的关系如式（12）所示：

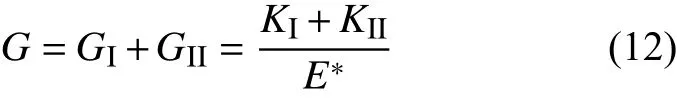
式中，

本工作认为裂纹尖端处于平面应力状态，因此有

在ABAQUS中进行XFEM疲劳裂纹扩展时，一旦疲劳裂纹开始扩展，裂尖单元将不复存在，之后的单元将成为贯穿单元。因此，在实际计算时，先计算前一个网格单元的裂纹尖端能量释放率范围，然后根据Paris公式计算其疲劳裂纹扩展速率，由此速率计算在下一个单元中，贯穿整个单元网格所需要的循环数。扩展方向通过计算选择贯穿下一个单元最快的方向作为扩展方向。

2.2 CTS 试样疲劳裂纹扩展分析

为了使模拟结果准确，建立与实验情况近似的有限元模型，将夹具也作为计算模型的一部分，将试件与夹具作为一个整体，这样既可以减少接触设置引起的计算量和误差，也可以保证裂纹尖端受载与实际情况相符。

采用ABAQUS建立几何模型并对其进行网格划分，单元类型采用C3D8R（8节点六面体缩减积分单元）。预制裂纹位于焊缝区，焊缝区的宽度为3 mm。图9给出α =60◦时的有限元模型及网格划分。

图9 时分网后的有限元模型Fig. 9 Meshed finite element model when

TC4-DT钛合金电子束焊接头的材料参数引用文献 [15]的数据，母材区：弹性模量 E1= 125 GPa，泊松比ν1= 0.34；焊缝区E1= 115 GPa，ν2= 0.34。利用基于能量线性软化的幂法则混合模型计算损伤演化，幂法则的指数为1。将夹具的一端固定，另一端施加与实验相同的循环载荷。模拟过程中与疲劳裂纹扩展起裂判据以及Paris公式相关的参数为：c1=c2= 0，其中c3、c4由实验拟合的 Paris公式得到，与1.3.2节方法相同，使用式（14）将应力强度因子转化为应变能释放率，拟合得到不同加载角度下如式（11）所示的以为参量的Paris公式，各加载角度下公式中参数如表4所示。

通过模拟计算可得到不同循环加载次数下疲劳裂纹的扩展行为。

2.2.1 疲劳裂纹扩展模拟结果

表 4 不同加载角度下以ΔG为参量复合型疲劳裂纹扩展Paris 公式参数Table 4 Parameters of Paris formula for mixed-mode fatigue crack growth under different loading angles based on ΔG

由图10可见，在拉剪复合载荷作用下，裂纹面初期沿焊缝水平扩展一小段（约1~2 mm），随即沿着与原裂纹面成一定角度的方向在焊缝区域内扩展，裂纹进入稳态扩展阶段，扩展角度不发生改变，扩展路径近似直线，此时的扩展角度即为开裂角。当裂纹扩展至焊缝与母材的界面处时，裂纹扩展路径发生偏折，裂纹沿着另一方向继续扩展。随着循环次数的增加，裂纹长度增加，等效应力强度因子增大，疲劳裂纹扩展速率也不断加快，到后期，随着Ⅰ型裂纹占主导，裂纹发生失稳扩展，方向改变，趋于Ⅰ型断裂模式，直至断裂。对于CTS试样，随着循环次数的增加，裂尖达到起裂条件后开始扩展，裂纹尖端出现应力集中，其Mises应力由中心向周围逐渐缩小，应力分布趋势与理论计算的塑性区形状大致相同。本工作模拟的加载范围属于裂纹尖端小范围屈服的线弹性范围，符合ABAQUS中XFEM疲劳裂纹扩展基于线弹性断裂力学的基本假设。