基于物元可拓法的培训机构人员流失风险预测

摘要：为了帮助中小型教育培训机构解决人员流失的问题，减少人员流动带来的经济损失、降低企业运营成本，建立了基于熵权法及改进物元可拓法的培训机构人员流失风险预测方法，在经典物元可拓模型的基础上，提出“极值最优点”的改进物元可拓模型，可为物元可拓模型中的极端经典域构建不同的关联函数，取得了关联度的最优拟合效果，并以A教育培训机构为例验证了改进物元可拓法的可行性。结果表明，应用改进物元可拓法研究人员流失问题可以从风险管理的角度帮助培训机构解决人员流失问题。研究方法为教育培训机构提高人力资源管理水平，加强组织管控能力，降低企业成本，增强企业盈利能力提供了新的思路。

关键词：决策理论;人员流失;风险预测;物元可拓法;培训机构

中图分类号：C934文献标识码：Adoi： 10.7535/hbgykj.2020yx01002

Staff turnover risk prediction of training institutions based on

matterelement extension method

LI Jingkang，WANG Xindi，GUO Xiaochun

Abstract：To help small and mediumsized education training institutions to solve the problem of staff turnover， reduce the economic consequences of the flow， and reduce business operating costs， based on the entropy weight method and improved matterelement extension method of training personnel loss risk prediction method is established. On the basis of the classical matterelement extension model， "extreme value most advantages" to improve the matterelement extension model is put forward. In the extreme classical field matterelement extension model， different correlation functions are built in order to obtain optimal fitting effect of the correlation. The feasibility of improved matterelement extension method is verified by A education and training institution as an example. Results show that the problem of brain drain is studied from the perspective of risk management by improved matter element extension method. To improve the level of human resources management， strengthen the ability to control the organization of this difficult problem education and training institutions has been given new ideas.

Keywords：decision theory; brain drain; risk prediction; matter element extension method;training agency

中小城市中的小型教育培訓机构作为教育市场的补充，为当地的经济发展做出了巨大贡献。小型培训机构在人员配制规模和经营状况上都无法和大型教育集团相抗衡，但相比大型集团的“自培优秀讲师”模式，小型培训机构大多聘请当地学校的教学名师，通过教学名师的知名度带动生源，其教学效果深受家长与学生们的认可。

将教学名师作为核心竞争力的同时，人才尤其是骨干人才的流失是所有培训机构在发展过程中都要面临的问题，是制约机构发展壮大的关键因素[1]。自立门户或被竞争机构高薪聘请都会造成教师的频繁变动，这不仅影响培训机构的教学质量与日常工作安排，还会引起生源的流失与教学口碑的下滑。因此，建立有效的人员流失预警机制，可以有效地避免核心竞争力的下降，同时根据预警结果调整机构的管理方式，也可以吸引更多优秀人才进入培训机构。

第1期李婧康，等：基于物元可拓法的培训机构人员流失风险预测 河北工业科技第37卷对教育培训机构人员流失问题的研究大多停留在因素分析、对策研究等定性研究层面。杜文博[2]结合莫布雷模型、心理契约等相关理论归纳分析AM机构人员流失原因并提出了相应对策。詹怡[3]和黄正[4]结合组织承诺理论、战略管理理论等人力资源相关理论，对中小型民营企业现存的人员流失问题进行分析，制定了相应的人力资源管理战略目标及实现方案。王健[5]指出中小民营企业人才对于薪水、晋升机会、福利的满意度与流失意图的相关关系较其他因素更为明显，培训机构无法提供可靠的福利保障是年轻教师流失的首要原因，并提出了具有实践性的管理策略。马熠[6]以FG培训机构为例，根据马奇和西蒙模型、普莱斯模型和扩展的莫布雷模型，构建了“员工流失风险识别”、“员工流失处理”、“措施反馈修正”的整套员工流失预警体系，从前期预警与后期管控方面着手，控制员工流失。李立安[7]以模糊物元的方法对知识型企业核心员工流失风险进行评价，构建了知识型企业核心员工流失风险指标体系。

笔者采用物元可拓法解决培训机构人员流失评价指标要素多样性和模糊性的问题。物元可拓法将物元分析与可拓集合相结合，广泛应用于地质、水文、电力、企业管理等领域，对于解决不相容的复杂问题、多指标综合评价模型具有很好的适用性，在理论研究和实践应用方面发挥了重要的作用[8]。赵永芳等[9]综合对比传统评价方法，研究了物元可拓法在地质灾害物元可拓模型中的应用。赵杰等[10]和LIU等[11]引入Hakanson毒性响应系数修正传统超标倍数赋权法权重、引入可变权重理论建立了基于改进物元可拓法的评价模型，并将其评价结果与传统评价方法结果进行对比。汤洁等[12]将物元可拓法应用于地下水水质评价，同时采用模糊综合评判方法进行了验证。李泓泽等[13]对物元可拓模型的经典域和待评物元以及最大隶属度准则进行改进，克服其在电能质量综合评价中的局限性和不足之处。在企业收购策略、公司运营绩效评价等经济领域验证物元可拓法的可行性与合理性，进而为有效提升企业组织水平与降低企业成本提供新思路和新方法[1415]。采用分层思想将风险评估的基本要素进行多指标因素分解，建立基于物元可拓的风险等级评价模型。实现定性到定量的转化描述出风险等级的偏向性[16]。

基于熵权法和物元可拓法，笔者从定性研究与定量研究相结合的角度提出“极值最优点”的改进物元可拓法，可为多指标综合评价方法中的不同指标构建关联度函数，构建培训机构人员流失预警模型，进而从风险管理的角度帮助中小型教育培训机构解决人员流失这一核心问题。

1基于熵权法及改进物元可拓法的培训机构人员流失风险预测

1.1经典物元可拓法的理论基础

物元可拓法用物元、特征、量值3个要素对事物进行描述，将待评物元记为N，物元特征记为C，特征量值记为V，则将有序三元组U=（N，C，V）作为描述研究对象量化特征的基本元，称为物元。当待评物元N具有多个物元特征时，可用n个特征量值（v1，v2，…，vn）描述对应的n个特征（c1，c2，…，cn），则物元U为n维物元。

物元可拓模型的建立包括4个步骤：确定经典域、节域与待评物元，建立关联函数，确定关联度，等级评定。人员流失评价指标共有n项，表示为（c1，c2，…，cn），人员流失风险预警可划分为m级，在第j级风险物元Uj中，vij为ci的取值为（aij，bij），称为经典域，在所有等级的风险物元Um中，vim为ci的取值为（aim，bim），称为节域。如Uj表示为

Uj=c1v1jc2v2jcivijcnvnj=c1（a1j，b1j）c2（a2j，b2j）ci（aij，bij）cn（anj，bnj）。                                         （1）

人员流失评价数据为n维物元U0，其中，（v1，v2，…，vn）为特征（c1，c2，…，cn）测评得到的实际数据。以vi与对应特征量有限区间的距离定量描述物元特征，記为关联函数ρ（vi，vij）与ρ（vi，vim），评价指标ci关于第j级风险级别的关联度记为Kj（vi），则有：

ρ（vi，vij）=12（aij-bij）+|vi-12（aij+bij）|，（2）

ρ（vi，vim）=12（aim-bim）+|vi-12（aim+bim）|，（3）

Kj （vi ）=ρ（vi，vij）ρ（vi，vim）-ρ（vi，vij），ρ（vi，vim）≠ρ（vi，vij），-ρ（vi，vij）|vij|，ρ（vi，vim）=ρ（vi，vij）。（4）

评价指标（c1，c2，…，cn）关于第j级风险级别的综合关联度为

Kj（P）=∑ni=1wiKj（vi）   ，                                                        （5）

其中wi为评价指标ci的权重。当Kj0（P）=max{Kj（P），j=1，2，…，m}，则认为P属于等级j0，对所有j，若存在Kj（P）≤0，则不计入等级评估。

1.2极值最优点的改进物元可拓法

在经典物元可拓模型中，由待评物元的特征量值到经典域的距离计算关联函数及关联度。即物元特征的特征量值属于某一等级的经典域时，由关联函数计算该特征量值到该经典域中点的距离。距离越近，则认为物元特征与该等级水平的隶属关系越明显。但在实际情况中，第一等级和最后等级的关联函数及关联度计算，存在着缺陷，当计算物元特征与第一等级或最后等级的隶属度、特征量值越接近该经典域的端点值，而不是经典物元模型采用的中点值时，物元特征与该等级水平的隶属关系明显。因此，笔者提出极值最优点的改进物元可拓法。

计算物元特征与第一经典域的隶属关系，其关联函数为

ρ（vi，vij）=12[（aij-bij）+|vi-aij|]，ρ（vi，vim）=12（aim-bim）+|vi-12（aim+bim）|。             （6）

计算物元特征与最后经典域的隶属关系，其关联函数为

ρ（vi，vij）=12[（aij-bij）+|vi-bij|] ，ρ（vi，vim）=12（aim-bim）+|vi-12（aim+bim）|。                               （7）

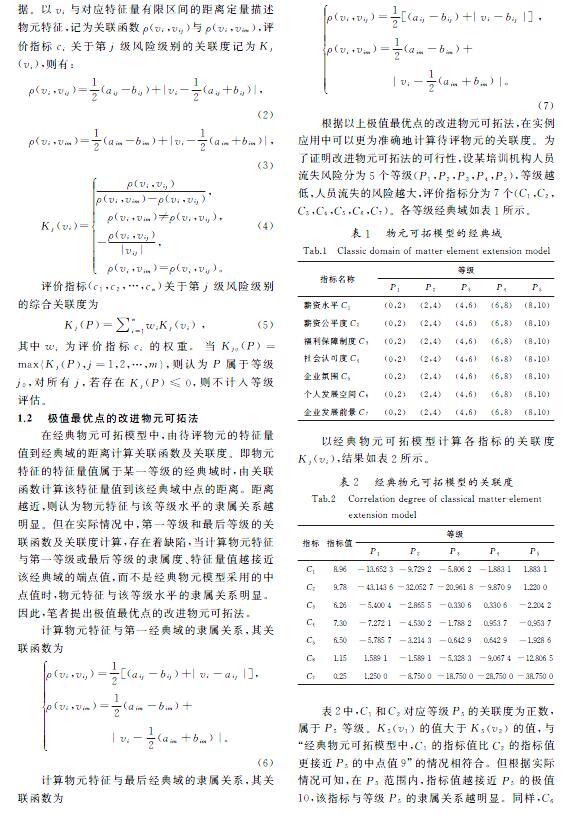
根据以上极值最优点的改进物元可拓法，在实例应用中可以更为准确地计算待评物元的关联度。为了证明改进物元可拓法的可行性，设某培训机构人员流失风险分为5个等级（P1，P2，P3，P4，P5），等级越低，人员流失的风险越大，评价指标分为7个（C1，C2，C3，C4，C5，C6，C7）。各等级经典域如表1所示。

以经典物元可拓模型计算各指标的关联度Kj（vi），结果如表2所示。

表2中，C1和C2对应等级P5的关联度为正数，属于P5等级。K5（v1）的值大于K5（v2）的值，与“经典物元可拓模型中，C1的指标值比C2的指标值更接近P5的中点值9”的情况相符合。但根据实际情况可知，在P5范围内，指标值越接近P5的极值10，该指标与等级P5的隶属关系越明显。同样，C6的指标值比C7的指标值更接近P1的中点值1，但在P1范围内，指标值越接近P1的极值0，该指标与等级P1的隶属关系越明显，即K1（v6）应小于K1（v7）。该经典物元可拓模型存在明显缺陷。

根据改进物元可拓模型计算各指标的关联度Kj（vi），结果如表3所示。

表中K5（v1 ）的值小于K5（v1 ）的值，指标C2相比指标C1，与等级P5的隶属关系更明显。与实际情况相符。同样，C7的指标值比C6的指标值接近P1的极值0，K1（v6 ）小于K1（v7 ）。与实际情况相符。由此证明，改进的物元可拓法可以更为准确地计算关联度。

1.3基于熵权法的指标权重确定方法

在进行培训机构人员流失风险等级评定时，只有确定了各评价指标的权重才能得到风险等级的综合关联度。笔者采用熵权法确定各指标权重。

熵权法是客观赋权法中被广泛应用的一种方法。业界普遍认为，信息熵可以反映信息的混乱、无序程度，即信息无序性越明显，蕴含的有用信息量越少，信息熵就越大。因此，根据熵值提供的信息量大小决定权重，以传递充足和有效的信息量，避免传统赋权方法，如层次分析法、专家调查法的主观性，较好地发现评价指标数据本身的信息特征，增强权重的可信度。熵权法具体包括4个步骤：归一化处理数据，确定信息熵，确定偏差度，确定指标权重。

对收集到的评价数据进行归一化处理，得到归一化矩阵为

P=A1A2…Aj…AmC1P11P21…P1j…P1mC2P21P22…P2j…P2mCkPk1Pk2…Pkj…PkmCnPn1Pn2…Pnj…Pnm，                          （8）

其中：Pkj=vkj∑mj=1vkj;vkj为对象Aj关于特征Ck测评得到的实际数据。

特征Ck的信息熵公式为

ek=-1ln m∑mj=1Pkj ln Pkj，                                      （9）

Ck的信息熵越大，代表評价指标的测评数据无序性越强，不同测评对象间的偏差越小，指标重要性越小。因此，计算各评价指标的偏差度，可以确定指标权重。偏差度公式为

δk=1-ek。                          （10）

权重向量W=（w1，w2，…，wk…，wn），其中：

wk=δk∑nk=1δk。                                                         （11）

熵权法通过发现评价指标数据本身的信息特征确定评价指标权重，是较为客观的赋权方法，因此采用熵权法来确定指标权重是可行的。

2实例分析

A教育培训机构成立于2018年1月，目前，拥有35名在职教师，辅导学生3 200余人次。为探究A公司的人员流失风险等级，笔者设计了“企业员工评价意见问卷表”，统计A公司教职员工对就职情况的满意程度，按1～10分填写。为了确保数据的真实有效性，发放调查问卷之前，笔者联系了A公司的全体教职工，说明此次调查对于员工本人及公司发展的意义，最终选择了25名自愿参加调查的员工作为评测对象（A1，A2，…， An）。

由于对中小型教育培训机构的人员流失问题研究尚处于初步阶段，笔者综合采用向春梅＼[1＼]和李立安＼[7＼]研究的评价体系，遵循敏感性、重要性、合理性、系统性原则，并与4位专家及培训机构经营者面谈、电话沟通，最终确定了由5个一级指标，12个二级指标构成的评价指标体系，其中“工作时间冲突”、“风险承受”、“工作强度”、“家庭负担”为“量小值更优”的指标，其余为“量大值更优”的指标，如图1所示。指标体系评估出的人员流失风险等级分为5个等级（P1， P2， P3， P4， P5），等级越低，人员流失的风险越大。

运用熵权法，进行定量分析，得到12项评价指标的权重W=（0105，0064，0145，0073，0055，0092，0027，0116，0030，0081，0111，0102） ，A培训机构人员流失风险评价指标原始数据如表4所示，将剔除一个最大值和一个最小值后的均值作为指标数据，如表5所示。

指标经典域为

U1=C1[0，2）C2[0，2）C12[0，2）;U2=C1[2，4）C2[2，4）C12[2，4）;

U3=C1[4，6）C2[4，6）C12[4，6）;U4=C1[6，8）C2[6，8）C12[6，8）;

U5=C1[8，10）C2[8，10）C12[8，10）。

根据表5中的数据，得到1组12维物元模型：

U0=C17.26C27.04C127.30。

将各指标数据代入关联函数计算关联度，则A公司的人员流失风险预警等级结果如表6所示。

其有效值为0.478 0，人员流失风险预警等级评定为P4。

3结论

笔者运用熵权法，从指标数据本身寻找信息特征，避免传统赋权方法的主观性，客观地赋予指標权重，作为培训机构人员流失风险预警模型的基础。在经典物元可拓模型的基础上，提出“极值最优点”的改进物元可拓模型，可为物元可拓模型中的极端经典域构建不同的关联函数，取得了关联度的最优拟合效果，克服了经典物元可拓法中极端经典域关联度计算结果与事实不符的缺点。以此对A培训机构人员流失风险水平进行了评价，结合定量研究与定性研究双重评估方式，充分利用了物元可拓法的优势，也为物元可拓法的改进应用贡献了思路。

通过对人员流失评价指标的选取、分解，以及对员工问卷调查的结果反馈，培训机构管理人员能够从整体上判断教职员工的心理状态与公司运营的整体情况，能够有的放矢地进行人力资源管理。通过风险预判的方式，避免人员流失这一问题的出现，从而提高人力资源管理水平，加强组织管控能力，增强企业盈利能力。

参考文献/References：

[1]向春梅. 中小培训机构人才流失原因及对策研究——以S机构为例[D].成都：西南交通大学，2017.

XIANG Chunmei. Causes and Countermeasures of Brain Drain in Small and Mediumsized Training Institutions [D].Chengdu： Southwest Jiaotong University，2017.

[2]杜文博. AM英语培训机构员工流失研究[D].西安：西北大学，2009.

DU Wenbo. The Study of Employees′ Turnover of AM English Training Agencies[D].Xi′an： Northwest University， 2009.

[3]詹怡. NH培训机构人力资源管理战略研究[D].西安：西安理工大学，2009.

ZHAN Yi. Study on NH Training Institutions Human Resources Strategic Planning [D]. Xi′an： Xi′an University of Technology，2009.

[4]黄正. 我国英语教育培训机构人力资源管理问题研究[D].南京：南京理工大学，2013.

HUANG Zheng. Human Resource Management of China′s English Education and Training Institutions Issues [D]. Nanjing： Nanjing University of Science and Technology，2013.

[5]王健. 中小民营企业人才流失成因分析及对策研究[D].北京：华北电力大学，2012.

WANG Jian. Causes Analysis and Countermeasure Research on Brain Drain in Mediumsized Private Enterprises[D]. Beijing： North China Electric Power University，2012.

[6]马熠. FG培训机构员工流失问题与对策研究[D].湘潭：湘潭大学，2014.

MA Yi. The Study on Problems and Countermeasures of the Staff Turnover of FG Training Institute[D].Xiangtan： Xiangtan University，2014.

[7]李立安. 知识型企业核心员工流失风险评价及策略研究[D].大庆：东北石油大学，2011.

LI Li′an. Research on the Evaluation and Counter Measures of Core Employees′ Loss Risk of Knowledgebased Enterprise [D]. Daqing： Northeast Petroleum University，2011.

[8]李祚泳.可拓论及其应用进展[J].大自然探索，1999（3）：6266.

[9]赵永芳，张凌云，于丽雅.基于熵权物元可拓模型的冲击地压安全评价[J].煤矿安全，2019，50（6）：213218.

ZHAO Yongfang， ZHANG Lingyun， YU Liya. Safety evaluation for rock burst based on entropyweight and matterelement extension model [J]. Safety in Coal Mines，2019，50（6）：213218.

[10]赵杰，罗志军，赵弯弯，等.基于改进物元可拓模型的鄱阳湖区耕地土壤重金属污染评价[J].农业环境科学学报，2019，38（3）：521533.

ZHAO Jie， LUO Zhijun， ZHAO Wanwan， et al. Assessment of heavy metal pollution in arable soils in the Poyang Lake area based on the improved matterelement extension method[J]. Journal of AgroEnvironment Science， 2019，38（3）：521533.

[11]LIU Shiliang， LI Wenping. Indicators sensitivity analysis for environmental engineering geological patterns caused by underground coal mining with integrating variable weight theory and improved matterelement extension model[J]. Science of the Total Environment，2019，686：606618.

[12]汤洁，李艳梅，卞建民，等.物元可拓法在地下水水质评价中的应用[J].水文地质工程地质，2005（5）：15.

TANG Jie，LI Yanmei，BIAN Jianmin，et al. Application of matterelement and extension to groundwater quality evaluation[J]. Hydrogeology and Engineering Geology，2005（5）：15.

[13]李泓泽，郭森，唐辉，等.基于改进变权物元可拓模型的电能质量综合评价[J].电网技术，2013，37（3）：653659.

LI Hongze，GUO Sen，TANG Hui，et al. Comprehensive evaluation on power quality based on improved matterelement extension model with variable weight [J]. Power System Technology，2013，37（3）：653659.

[14]张刚，李芳锋，张江滨，等.基于改进模糊物元法的电力自供区最优收购策略[J].西安理工大学学报，2018，34（2）：178184.

ZHANG Gang，LI Fangfeng，ZHANG Jiangbin，et al. Optimal acquisition strategy for electricity selfsupply area based on the improved fuzzy matterelement method [J]. Journal of Xi′an University of Technology，2018，34（2）：178184.

[15]余顺坤，武晓龙，刘琳.基于物元可拓法的子分公司高管绩效管控模型研究[J].管理世界，2017（3）：182183.

[16]骆建波. 基于物元可拓的风险等级评价方法研究[C]//2018第七届全国安全等级保护技术大会论文集，北京：北京市海淀区太极计算机培训中心，2018：5.

收稿日期：20191022;修回日期：20191120;责任编辑：张军

基金項目：纵向预研基金——其他部市（KBI13058531）

第一作者简介：李婧康（1996-），女，河北唐山人，硕士研究生，主要从事信息管理及信息系统方面的研究。

通讯作者：王馨迪副教授。 Email：xdwang@bjtu.edu.cn

李婧康，王馨迪，郭晓淳.基于物元可拓法的培训机构人员流失风险预测 [J].河北工业科技，2020，37（1）：510.

LI Jingkang，WANG Xindi，GUO Xiaochun.Staff turnover risk prediction of training institutions based on matterelement extension method[J].Hebei Journal of Industrial Science and Technology，2020，37（1）：510.