一种以扭转系数KS实现谐振响应分析的方法

李良，范启富，徐金仙

一种以扭转系数K实现谐振响应分析的方法

李良1,2，范启富1，徐金仙3

（1.上海交通大学 电子信息与电气工程学院自动化系，上海 200240；2.松下电器机电（中国）有限公司，上海 200120；3.上海浩蕊峰自动化设备有限公司，上海 201204）

以精密机床的机械谐振响应特性研究为出发点，以电机动子及负载作为两个惯性系统、通过扭转系数作为衔接，对惯性系统的扭转特性进行建模，分析机械谐振特性与上述变量之间的相关特性。给出了一种以扭转系数为基础的谐振系统谐振响应分析方法，建立了数学模型，进一步引申到伺服控制系统的闭环特性，通过MATLAB对不同惯性、扭转系数组合的闭环特性进行频率分析，解构机械谐振发生的机制，并在线性模组的测试中获得验证。

扭转系数；惯量；弹性模量；谐振响应特性

在数控机床等需要高精度传动控制场合，电气系统增益的提升受到机械谐振特性响应的限制，提升至一定程度会出现系统振荡，增益无法继续提高，限制了整个传动系统的响应特性。为改善响应特性，文献[1]提出了惯量必须匹配的观点，文献[2-3]提出了惯量比的合理取值，文献[4]提出了基于PI的谐振抑制方式，文献[5]则用达朗贝尔原理给出了刚体基于惯性力平衡的动力学模型，基于这种方法更容易建立扭转系动力学模型。

为了提升效率和加工质量，传动部件的系列化、标准化、智能化设计是未来趋势[6]。高效、精密的机械设计过程中，需要一种简洁的方法，将扭转系数K和期望的谐振特性范围引入到传动器件的机械设计中去。

以数控机床为例，典型传动方式由电机、联轴器、丝杆、导轨模组组成，经典的传动模型无法分析谐振的发生特性。尝试通过引入扭转系数K，从扭转系数、负载惯量对于闭环系统响应带宽影响的角度分析传动系统谐振发生特性。

1 传动系统动力学模型及传动系统扭转模型

理想的传动模型是K电机转子和负载为纯刚性连接，即转子所转过的角度与负载在任何时刻都是同步的，然而，实际的传动连接必然存在弹性扭转。假定电机和负载之间存在弹性扭转连接，扭转角度为，传动模型如图1所示。

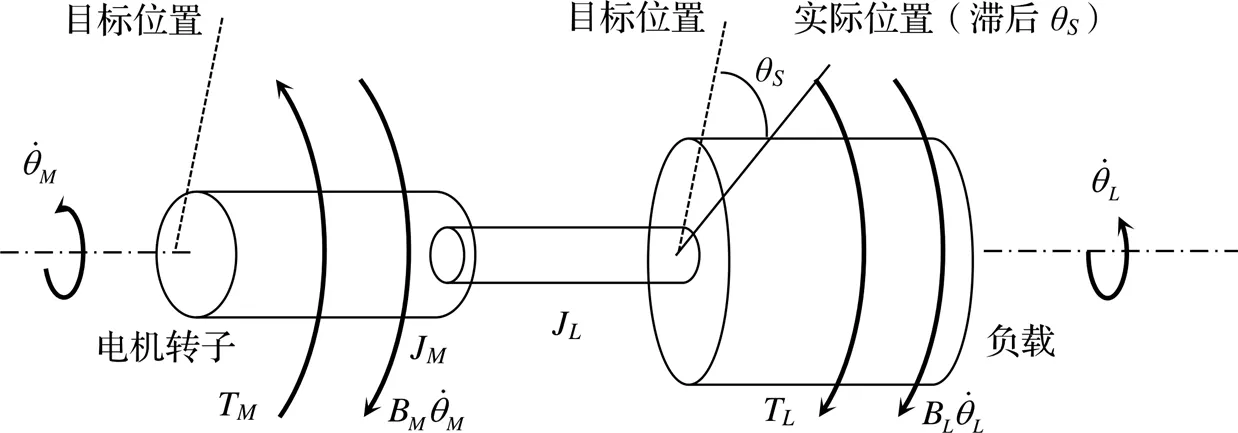
图1 传动系统模型

图1中电机转子和负载作为两个不同的惯量系统，以扭转系数K作为衔接，建立传动扭转模型如图2所示。

图2 传动系统扭转模型

电机驱动的负载包括电机本体的惯量J和之外的J。

运动方程[9]为：

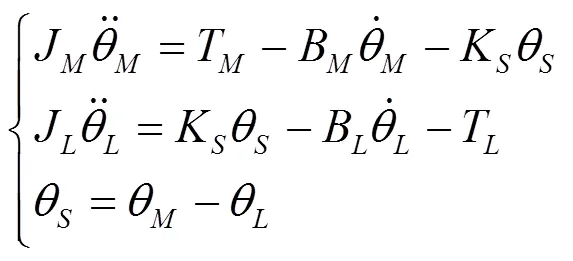
假设理想状态下粘滞摩擦系数为0，外部扰动力矩为0，消去扭转角度变量可以获得：

式中：为拉式变换的复参变量。

其中，扭转系数模型为：

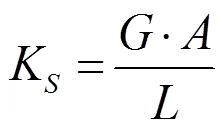
式中：为扭转弹性模量，GPa；为扭转处横截面的扭转常量（Torsion Constant），与截面形状和面积大小相关；为负载的长度，指与柱状连接负载发生扭转部分的长度。

为便于分析，简化速度环增益为K、电流环增益为K，构造伺服电机控制的速度闭环控制回路如图3所示。

为速度指令；为转矩电流指令；为速度偏差，；KV为速度环增益；KC为电流环增益

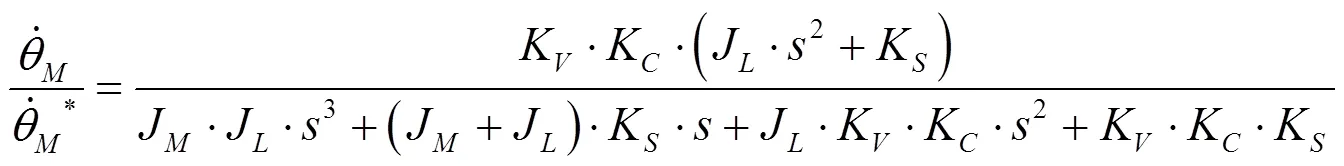
2 通过仿真系统来模拟（，）闭环系统传动模型的响应曲线

获得系统的数学模型之后，通过MATLAB仿真，可以比较直观地获得谐振频率的响应特性分析，建立参数对照组，根据模型的三个主要变量：J、J、K，设计不同组合的对照组。

Case1：低J、低J、低K的频率响应。

Case2：低J、高J、低K的频率响应。

Case3：低J、高J、高K的频率响应。

Case4：低J、低J、高K的频率响应。

Case5：高J、低J、高K的频率响应。

如表1所示。

因已知闭环传递函数，代入J、J、K参数后，容易获得如图4所示频率响应曲线的仿真结果。

表1 仿真所采用的参数组

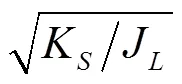
由此明确，通过扭转系数K负载惯量J以及电机转子惯量J实现频率响应分析可行。通过式（5），并定义惯量比＝J/J，对传递函数进行重构为：

定义：

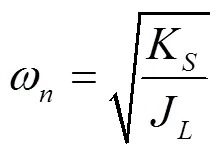
式（6）可表示为：

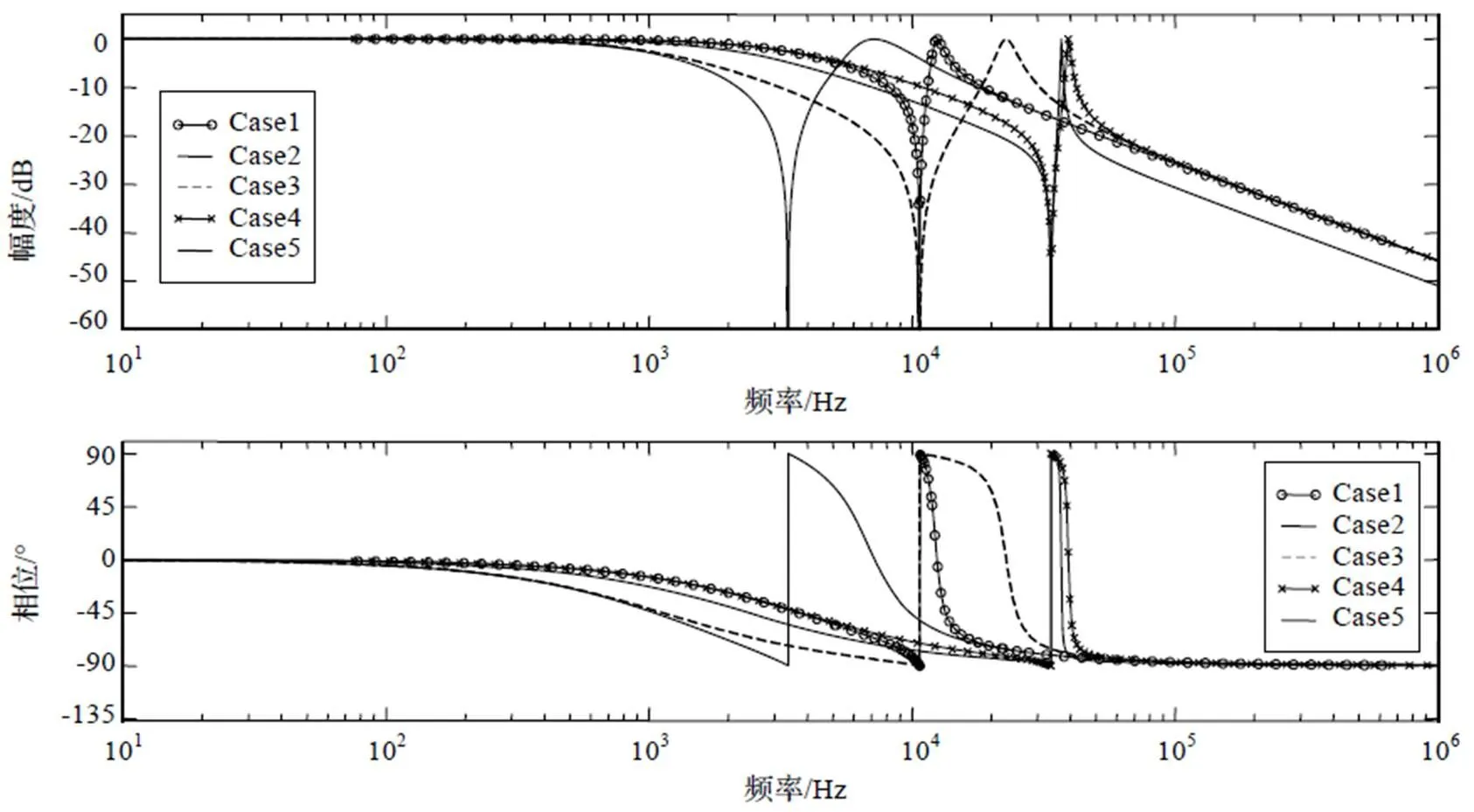
图4 不同参数的闭环频率响应

令：

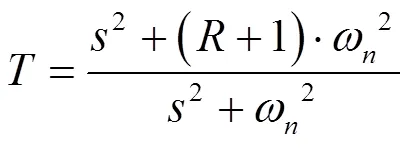
此时式（8）可表示为一阶形式：

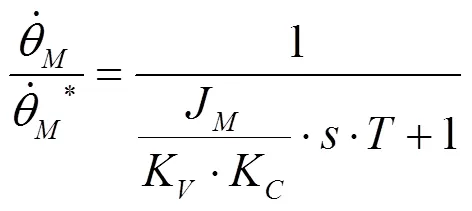
由式（9）可见，当≠ω时，惯量比在系统中起到了时间常数调整的作用。

由上述仿真及分析，可得结论：通过扭转系数K的分析可以获得谐振频率响应特性，而惯量比在其中起到了时间常数的作用。

3 实验对比

图5为测试系统的系统构成框图，期望通过其中扭转系数K的变化，来验证扭转系数对于频率响应的影响特性。实验中，保证负载惯量不变，电机与负载连接的部分联轴器采用外径、长度相同的规格，根据式（4）对于扭转系数的定义，K的唯一影响因素为电机的轴径。

对实验内容进行说明：

测试负载采用图6的丝杠模组，测试过程中不对丝杠模组进行更换，仅更换电机和联轴器，传动系统的构成为：①伺服电机，②联轴器，③丝杠模组、螺母副及直线导轨。

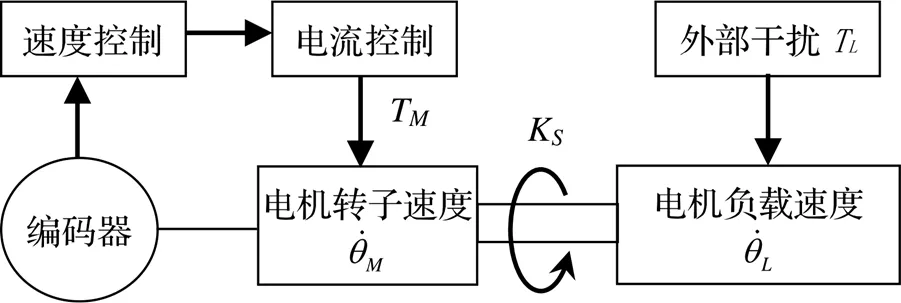
图5 测试系统构成示意图

图6 滚珠丝杆直线模组

（1）伺服电机

电机一和电机二如图7、表2所示。

（2）联轴器

联轴器一：内径11 mm；外径30 mm，长度40 mm。

联轴器二：内径14 mm；外径30 mm，长度40 mm。

（3）丝杠模组、螺母副及直线导轨

丝杠：长度500 mm，直径10 mm，导程5 mm；螺母副及导轨为直线模组的配套件。

速度闭环响应的测定：速度闭环响应为伺服电机对于速度指令的响应，通过控制系统发送速度指令，指令反馈通过编码器的位置信息进过一次微分后获得。

图7 直径不同的两组电机

速度闭环测试的响应频率分析可采用伺服电机厂家提供的FFT（Fast Fourier Transform，快速傅里叶变换）测定工具测定。FFT测试是通过对速度闭环系统发送振幅固定的一系列正弦速度指令，并采集相应的系统反馈速度，采用快速离散傅里叶变换的方式提取闭环系统的频率特征，即伯德图。

闭环速度频率响应如图8、图9所示。

表2 不同轴径下两组测试参数的比较

图8 电机一的频率响应特性曲线

-3 dB截止频率作为闭环系统频率响应特性的判断依据，可以通过伺服驱动器厂家的FFT速度闭环频率特性测定软件经过频率特性测试获得。

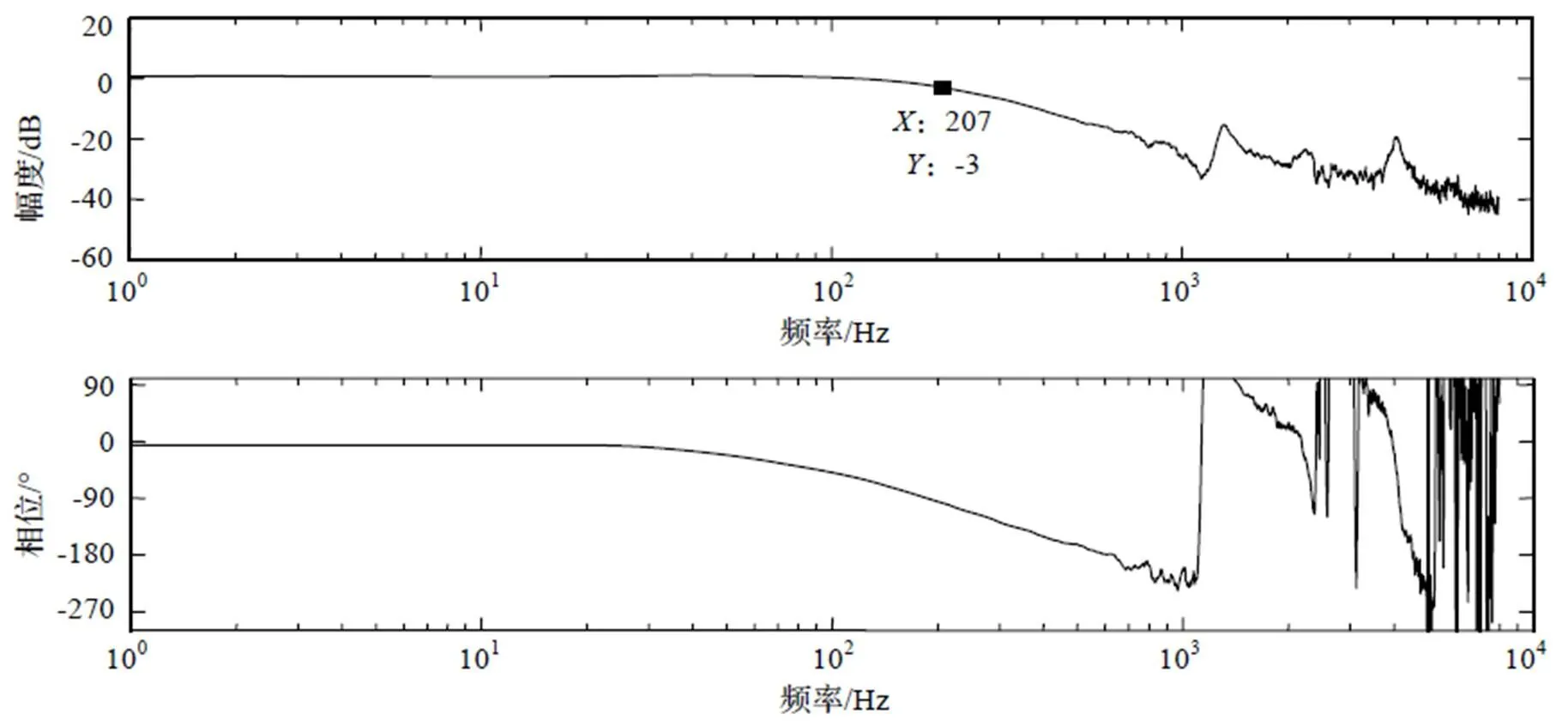
图9 电机二的频率响应特性曲线

至此，本实验揭示了扭转系数K对于频率响应的影响，从而证实了通过扭转系数K实现谐振响应分析的可行性。

进一步证明上述结论需要区分转子惯量、转子半径、转子材质进行定量分析。本测试在一定程度上可说明扭转系数K及负载惯量J对于传动系统响应带宽的影响，为进一步分析传动系统谐振响应带宽改善提供了一种思路。

4 总结

本文从扭转系数K的角度，分析传动系统的谐振响应特性，旋转传动机构的响应带宽受到传动轴的半径、材质、长度、负载的惯量的重要影响。提出了一种通过分析扭转系数特性，实现改善传动系统谐振响应特性的方法。改善传动系统的谐振响应特性，可以从连接部分的材料、横截面积以及缩短负载的长度着手，具体的实施方法比如选择轴径更大的电机、刚度更大的联轴器、长度更短的丝杠，并尽可能地减小负载的整体惯量。

[1]余清华. 数控机床进给系统必须惯量匹配[J]. 金属加工，2011（3）：53-54.

[2]黄捷建. 伺服电机负载惯量比的合理取值[J]. 微电机，2017，50（11）：72-75.

[3]黄梁松，曲道奎，徐方. 基于可调惯量比的伺服系统低频谐振控制[J]. 电气传动，2010，40（7）：61-65.

[4]王璨，杨明，徐殿国. 基于PI控制的双惯量弹性系统机械谐振的抑制[J]. 电气传动，2015，45（1）：49-53.

[5]郑慧明. 刚体动力学的统一分析格式[J]. 机械，2018（1）：24-28.

[6]李金佩，姚慧，白瑀，等. 典型传动机械零件参数化设计系统方法研究[J]. 机械，2018（4）：11-14.

[7]孙宇，王志文，孔凡莉，等. 交流伺服系统设计指南[M]. 北京：机械工业出版社，2013.

[8]Jeff Moscrop. An analysis of motor/load inertiamismatch in machine tool servo systems[C]. In 1stIFAC Conference on Mechatronic System，2000.

[9]Jeff Moscrop. Control of Servo Systems in the Presence of Motor-Load Inertia Mismatch[C]. The 27th Annual Conference of the IEEE Industrial Electronics’ Society，2001.

[10]Liangsong Huang. Adjustable Inertia Ratio Control for Low-Frequency Torsional ResonanceSuppression in industrial servo system[C]. 2010 International Conference on Measuring Technology and Mechatronics Automation，2010.

Method of Resonant Response Analysis Based on Torsion CoefficientK

LI Liang1,2，FAN Qifu1，XU Jinxian3

( 1.School of Electronic Information and Electrical Engineering, Shanghai Jiaotong University, Shanghai 200240, China; 2.Panasonic Industrial Devices Sales (China) Co., Ltd., Shanghai 200120, China; 3.Shanghai Haoruifeng Automation Equipment Co., Ltd., Shanghai 201204, China )

On the basis of the research on the mechanical resonance response characteristics of the precision machine tool, this paper takes the motor rotor and load as two different inertial systems, and connects them with the torsional coefficientK. As a result, the torsional characteristics of the inertial systems are modeled, and the relevant characteristics between the mechanical resonance characteristics and the above variables are analyzed. This paper presents a method of resonance response analysis of resonance system based on torsion coefficientK, establishes a mathematical model which is further extended to the closed-loop characteristics of servo control system, analyzes the closed-loop characteristics of the combinations of different inertia and torsion coefficient by MATLAB, and deconstructs the mechanism of mechanical resonance which is later verified in the test of linear module.

torsion coefficient；inertia；elasticity modulus；resonant response characteristics

TG659

A

10.3969/j.issn.1006-0316.2020.03.003

1006－0316 (2020) 03－0014－06

2019－10－09

李良（1982－），男，上海人，硕士研究生，主要研究方向为伺服电机在精密机床中的改善、运动控制理论；范启富（1962－），男，山西太谷人，博士，副教授，主要研究方向为振动、运动控制、FPGA在控制与信号处理中的应用；徐金仙（1971－），女，浙江金华人，硕士，高级工程师，主要研究方向为精密机械及仪器仪表。