多圈缠绕柔索最大传递扭矩的影响因素

曾琴，朱建公

多圈缠绕柔索最大传递扭矩的影响因素

曾琴，朱建公

（西南科技大学 制造科学与工程学院，四川 绵阳 621000）

柔索传动具有结构简单、布局灵活等优势，是解决小回转空间内大扭矩传递较有效的传动方式。针对柔索传动传递能力提高的问题，开展了对柔索最大传递扭矩影响因素的研究，得出最大传递扭矩与预紧力、包角、摩擦系数、弯曲半径和柔索半径比、螺旋升角有关。通过数值分析、正交试验和ANSYS Workbench接触分析，得出小回转空间内多圈缠绕柔索最大传递扭矩受包角影响最大，其次是预紧力、摩擦系数，但包角大于10π后，最大传递扭矩不再随包角的增加而增大。相比较而言，弯曲半径和柔索半径比、螺旋升角对最大传递扭矩影响较小。

小回转空间；多圈缠绕柔索；最大传递扭矩，接触分析

柔索传动具有结构简单、布局灵活、传动平稳、低空回等优势，广泛运用在机器人执行部件、特殊环境工作机械臂、光电平台精密指向机构、微创手术末端器械等设计中，如四足步行机器人TITAN-VIII[1]、光电侦察吊舱、DLR-II灵巧手等。柔索传动作为一种新型传动方式，其研究尚未形成完整理论体系，文献[2]分析了预紧力、摩擦系数、传动包角、弯曲刚度等对柔索传动精度的影响，文献[3]对柔索传动绳槽匹配进行了研究，文献[4]研究得出柔索传动特性与主要设计参数的内在关系，文献[5]对柔索传动的张力进行了分析与测量，文献[6]分析了预紧力和负载对钢丝绳传动精度的影响，文献[7]分析了弹性体的变形和传动部件机械加工精度对弹性体精密传动传动比的影响。在对柔索传动特性的研究中，学者们基于缠绕圈数小于1圈时的柔索最大传递扭矩影响因素进行了探究，而对多圈缠绕柔索没有涉及，因此开展多圈缠绕柔索最大传递扭矩影响因素的研究，对柔索传动的研究设计和提高柔索传递能力都有一定的参考意义。

1 多圈缠绕柔索结构

柔索传动是解决小回转空间内大扭矩传递较有效的传动方式，但空间距离小、装置预紧力有限、柔索抗拉力低等因素限制了柔索传递扭矩的能力。

图1 某扳手的末端执行部件

如图1所示，部件中柔索将主动轮上的扭矩传送到从动轮上，从动轮带动其腔内的螺母连续正反转，实现螺母的装卸。受螺栓所在装配空间的限制，螺母所在空间最大回转半径不超过12.5 mm，轴向移动距离不超过16 mm。在这种特殊工作环境下，通过多圈缠绕并根据空间限制合理布置柔索的缠绕方式，不仅可以减小从动轮轴因柔索张力引起的变形，还可以将传递扭矩提升至50 N·m。

2 多圈缠绕柔索最大传递扭矩

2.1 多圈缠绕柔索受力分析

传统柔性体传动力学尤拉公式由于忽略柔索直径且假设柔索完全柔软[8]，不适用于转动轮回转半径小、传递大扭矩的场合。在考虑柔索直径和弯曲刚度的情况下，对接触段柔索微元进行受力分析如图2所示。

图2 接触段柔索微元受力分析

在转动轮底面建立直角坐标系，接触段柔索微元投影如图3所示。

忽略柔索重力、离心力、弯曲阻力，建立力学平衡方程为：

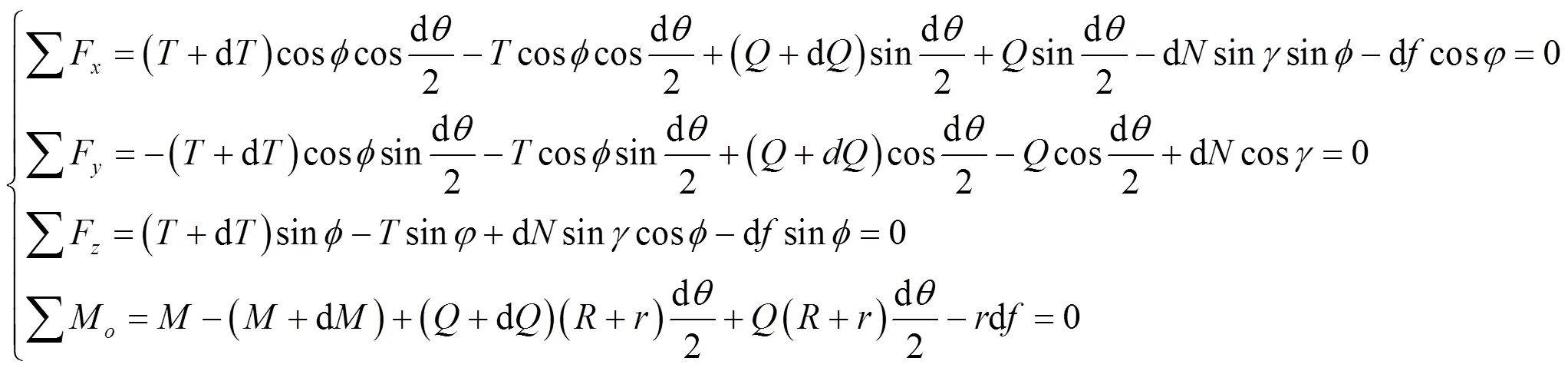
式中：T为张力，N；N为正压力，N；Q为剪切力，N；df为摩擦力，N；M为弯矩，N·m；φ为螺旋升角，rad；γ为正压力与柔索轴线的夹角，rad；θ为包角，rad；r为柔索半径，mm；R为转动轮半径，mm。

基于柔索和转动轮之间线性摩擦，有：

式中：为摩擦系数。

由于d为无穷小量，所以有式（3）：

基于线性弯曲假设，弯曲扭矩只取决于弯曲刚度和弯曲半径，而与包角无关，则有：

将式（2）～式（5）代入式（1），得拉力的二阶常系数线性齐次微分方程和一阶导数：

式（6）通解表达式为：

取1＝(0)、(0)＝0为特解求得入绳端张力T和出绳端张力2的比值为：

2.2 各参数对最大传递扭矩的影响

由于预紧力0＝(1＋2)/2，根据螺母所在空间最大回转半径为12.5 mm，得出柔索不打滑时的最大传递扭矩max为：

根据式（9）、式（10）可知柔索不打滑时能传递的最大传递扭矩max与预紧力0、包角、弯曲半径和柔索半径比、摩擦系数、螺旋升角有关，各参数与最大传递扭矩的关系如图4所示。

由图4（a）～（c）可得，最大传递扭矩随预紧力、包角、弯曲半径和柔索半径比、摩擦系数的增大而增大，但包角大于10π后，最大传递扭矩不再随包角的增加而增大；由图4（d）可得，最大传递扭矩随螺旋升角的增大而减小，螺旋升角对最大传递扭矩影响较小，可以忽略不计。

为满足柔索抗拉强度要求，增大预紧力的同时也要增大柔索半径，柔索半径的增大则会导致弯曲半径和柔索半径比减小。针对多种因素同时影响最大传递扭矩，通过正交试验找出主要影响因素并进行因素的优化配置，可以有效提高柔索传递能力。由式（10）可得，要实现最大传递扭矩为50 N·m，则预紧力不得低于2000 N，根据柔索最小破断拉力公式，确定弯曲半径和柔索半径比不大于17，为满足柔索使用原则，取弯曲半径和柔索半径比不小于15，则预紧力不得高于2600 N。取钢和钢之间的摩擦系数为0.1～0.2，正交试验结果及分析如表1所示。

由表1和图4可知，小回转空间内多圈缠绕柔索最大传递扭矩受包角影响最大，其次是预紧力、摩擦系数，相较而言，弯曲半径和柔索半径比、螺旋升角对最大传递扭矩影响较小。

3 基于ANSYS Workbench的接触分析

采用ANSYS Workbench对不同包角、摩擦系数、预紧力下的多圈缠绕柔索结构进行接触分析，得出其接触应力、摩擦应力的分布规律及大小。

转动轮和柔索的主要参数如表2所示。

柔索和转动轮接触面类型为Frictional[9]，对转动轮和钢丝绳分别采用6面体和4面体网格划分，在求解控制中打开大变形开关，设置边界条件，得到不同参数下接触应力和摩擦应力分布规律及大小如图5所示。

由图5可知，小回转空间内多圈缠绕柔索最大传递扭矩受包角影响最大，但包角大于10π后，最大传递扭矩不再随包角的增加而增大。

4 结论

小回转空间内多圈缠绕柔索最大传递扭矩受包角影响最大，其次是预紧力、摩擦系数，相比较而言，弯曲半径和柔索半径比、螺旋升角对最大传递扭矩影响较小。

图4 各参数与最大传递扭矩的关系

表1 正交试验结果及分析

主次顺序：A＞D＞C＞B；优组合：A3B2C3D3

表2 材料参数

小回转空间内多圈缠绕柔索传动中，增大包角可以有效地提高柔索最大传递扭矩，但包角大于10π后，最大传递扭矩不再随包角的增加而增大，原因在于多圈缠绕柔索结构达到一定圈数后会发生欧拉衰减效应[10]。

本文未考虑转动轮螺旋槽参数对最大传递扭矩的影响，螺旋槽的形状、深度、宽度等参数对最大传递扭矩的影响还有待探究。

[1]Hirose S，Arikawa Keisuke. Development of quadruped walking robot TITAN-VIII for commercially available research plat for m[J]. Journal of the Robotics Society of Japan，1999，17（8）：1191-1197.

[2]JaimeWekmeister，Alexander Slocum. Theoretical and experimental determination of capstan drive stiffness[J]. Precision Engineering，2007，31（1）：55-67.

[3]罗护，沈军，盛德军. 微型钢丝绳传动绳槽匹配及设计方法研究[J]. 机械科学与技术，2010，29（3）： 329-332.

[4]鲁亚飞. 精密柔索传动机理与设计方法研究[D]. 长沙：国防科学技术大学，2013：38-44.

[5]谢馨，祁超，江献良，等. 精密柔索传动张力的分析与测量[J].光学精密工程，2018，26（10）：2423-2429.

[6]张洪文，曹国华，李延伟，等. 钢丝绳传动在航空光学遥感器上的应用[J]. 激光与红外，2013，43（4）：418-422.

[7]郑飞，丁亚林，李娜，等. 基于某航空遥感器同步传动机构的精度分析[J]. 武汉理工大学学报，2010，32（6）：50-53.

[8]张芹. 多绳摩擦提升机的防滑问题探讨[J]. 煤矿机械，2007，28（5）：50-51.

[9]王强. 基于ANSYS WorkBech一字型转轴扭矩分析[J]. 机械，2018，45（7）：25-27.

[10]江祺琦，孟光，王建明. 卷扬机钢丝绳欧拉公式及欧拉衰减的研究[J]. 力学研究，2016，5（1）：10-16.

Influencing Factors of Maximum Transmission Moment of Multi-Lap Winding Cable

ZENG Qin，ZHU Jiangong

( School of Manufacturing Science and Engineering,Southwest University of Science and Technology, Mianyang 621000, China )

Cable drive is an effective transmission mode to realize the transmission with large moment in small rotating space because of its simple structure and flexible layout .In order to improve the transmission capacity of cable drive, the influencing factors of the maximum transmission moment of cable are studied, and it is concluded that the maximum transmission moment of cable is related to pretension, angle of contact, friction coefficient, bending radius, radius ratio and helix angle. Through numerical analysis, orthogonal test, contact analysis and ANSYS workbench, it is concluded that the maximum transmission moment of multi-lap winding cable is most affected by angle of contact, followed by pretension, friction coefficient in small rotating space, but when the angle of contact is more than 10π, the maximum transmission moment no longer increases with the angle of contact.

small rotating space；multi-lap winding cable；the maximum transmissi moment；contact analysis

TH132.3；V263.2

A

10.3969/j.issn.1006-0316.2020.03.004

1006－0316 (2020) 03－0020－06

2019－10－24

曾琴（1989－），女，四川乐山人，硕士研究生，助理讲师，主要研究方向为机械设计制造及其自动化。