基于TPMS建模方法进行仿生骨支架结构设计

石张傲，周鑫

基于TPMS建模方法进行仿生骨支架结构设计

石张傲，周鑫

（四川大学 机械工程学院，四川 成都 610065）

为了更好地拟合出人体骨细胞生存生长的多孔曲面环境，采用基于函数的极小三周期曲面（TPMS）建模方法，来进行仿生骨支架结构的设计。采用这种方法，能够通过调整函数的相关参数，实现对仿生骨支架孔径大小以及孔隙率大小的精准控制。选取了TPMS结构中的一种P曲面结构，通过与人体真实骨组织结构单元孔径大小以及孔隙率大小进行比对，选定了P曲面结构的参数值，并确定了仿生骨支架合理的单元尺寸，最后通过有限元仿真软件对模型进行了力学分析及评估，结果表明，设计的支架结构具有更匹配人体骨结构的力学性能，对指导构建人工骨支架结构具有重要意义。

TPMS；人工骨支架；有限元分析

由于意外创伤、疾病感染、骨肿瘤手术清除等多种原因，临床上骨缺损问题[1]日益严重，患者越来越多，目前，自体骨移植[2]仍然是治疗骨缺损疾病的最佳选择，因为自体骨具有良好的组织相容性，并且不用考虑排斥性，但自体骨移植也有很大的弊端和局限性。首先，自体骨移植供给部位供给量有限；其次，会大大增加手术区域和手术时间；最后，大面积的手术会增加疾病感染以及造成术后不适等并发症的风险。因此，人们开始寻求新的方法来解决这一系列的问题。

随着科技的进步，尤其医学3D打印技术取得的成功，推动了骨组织工程学[2-5]的发展，人工骨支架结构成为骨组织工程学的研究重点，传统意义上用于临床的骨支架结构[6-7]，多为无孔隙的硬金属块状结构，仅仅起到填补缺损的作用，或作为一些规则形状的支架结构，如正方体、钻石立方和蜂窝状等。这些结构虽然简单、便于设计和制备，但很明显和真实人体骨细胞生存的复杂曲面的三维贯通的多孔结构具有很大差异，植入人体后，不能令人满意。

作为骨细胞生长的支撑结构，骨支架应是表面光滑贯通无扭曲或尖锐棱角的多孔结构，便于细胞在支架上的附着和增殖。很多研究表明[8]，多孔骨支架结构孔径、孔隙率对结构的力学性能、骨细胞后续的渗入、附着增殖都有至关重要的影响。极小三周期曲面（TPMS，Triply Periodic Minimal Surface）[9-11]上各点平均曲率均为零，表面平滑光顺，在空间三个方向上周期分布，孔与孔之间相互贯通。曲面的结构形状由隐函数表达式确定，改变函数的参数可以方便地调整孔径以及孔隙率的大小，得到满意的支架结构。基于这些优点，选择极小周期函数的建模方法设计骨支架模型结构具有重大意义。

本文重点研究TPMS结构中的P曲面结构，通过改变函数表达式参数，得到匹配原生骨力学性能，并且孔径、孔隙率满足骨细胞生存条件的支架结构。

1 模型结构的设计

1.1 具有代表性的几组TPMS结构

TPMS结构均由隐函数表达式确定，其中具有代表性的几组曲面结构表达式分别为：

式中：a、b、c、μ均为常数，＝1,2,3,4。

当给a、b、c赋值为1，μ赋值为0时，就能得到TPMS结构中典型的基本单元结构，如图1所示。

1.2 多孔结构孔隙率的计算

孔隙率是固体结构中孔隙空间所占百分比，其计算公式为：

式中：V为多孔模型总体积；V为多孔模型孔隙总体积。

孔隙率的测量方法有多种，常见的有显微分析法[12-13]和称重法[14]，显微分析法要求多孔材料的样品截面尽量平整，通过显微镜或显微CT的方式获得样本的截面。然后统计样本的总面积S和包含孔隙的面积S，将体积比转化为表面积比。称重法通过称量模型样品的重量，将模型体积比转化为样品密度比，同样可行。在实际的操作中，由于使用的三维软件具有强大的测量功能，可以直接测出两部分体积，通过计算两部分体积比直接得到模型孔隙率。

1.3 改变函数参数得到理想的P结构模型

骨支架的孔径、孔隙率，对骨细胞生长及后续骨组织长入有很明确的影响，据研究[15-16]，当孔径为200～1200 μm、孔隙率为50%～80%，适合骨细胞渗入、附着、增殖。进一步分析表明[17-18]，孔径为400～1000 μm、孔隙率为55%～75%，与人体骨组织结构更类似，更利于骨组织长入。根据前面给出的P曲面表达式，当＝1、＝1、＝1，而取不同的数值时，可以直观看到单元模型孔径、孔隙率的变化情况，图2是当＝0、0.3、0.5、0.8、1.0时，P曲面单元结构的变化，这些变化给研究带来了很多启发。这仅仅只是改变了一个参数，如果同时改变几个参数，或者函数表达式进行一些调整，带来的变化更大。

为了更加直观地得到参数值的变化对单元模型孔径、孔隙率的影响，设计单元细胞结构尺寸为1.5×1.5×1.5 mm，测量分析计算得到＝0、0.3、0.5、0.8、1.0时孔径、孔隙率的具体数值，为后续支架的结构设计选择更加合理的单元结构，以及更加准确的参数值。如图3所示。

图1 TPMS典型的四组单元结构

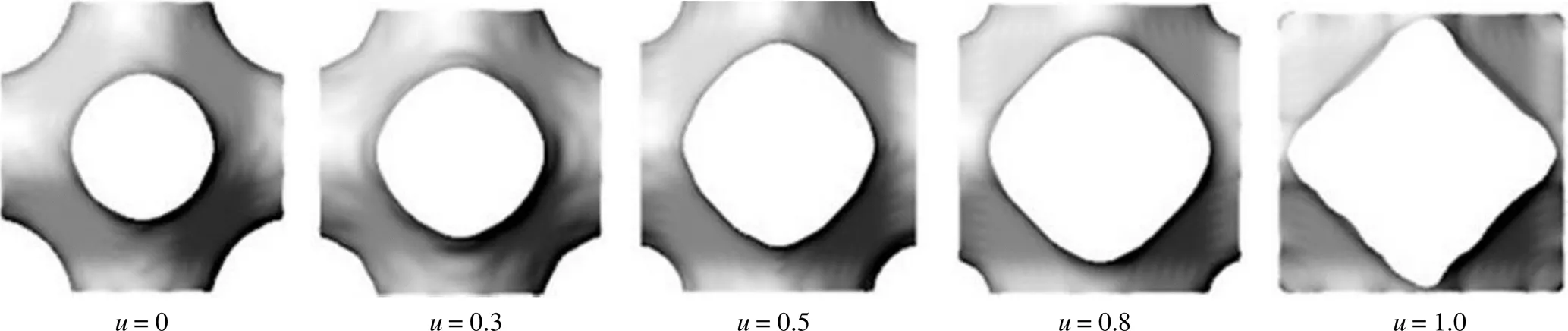
图2 单元结构随参数u值的改变做一定规律的变化

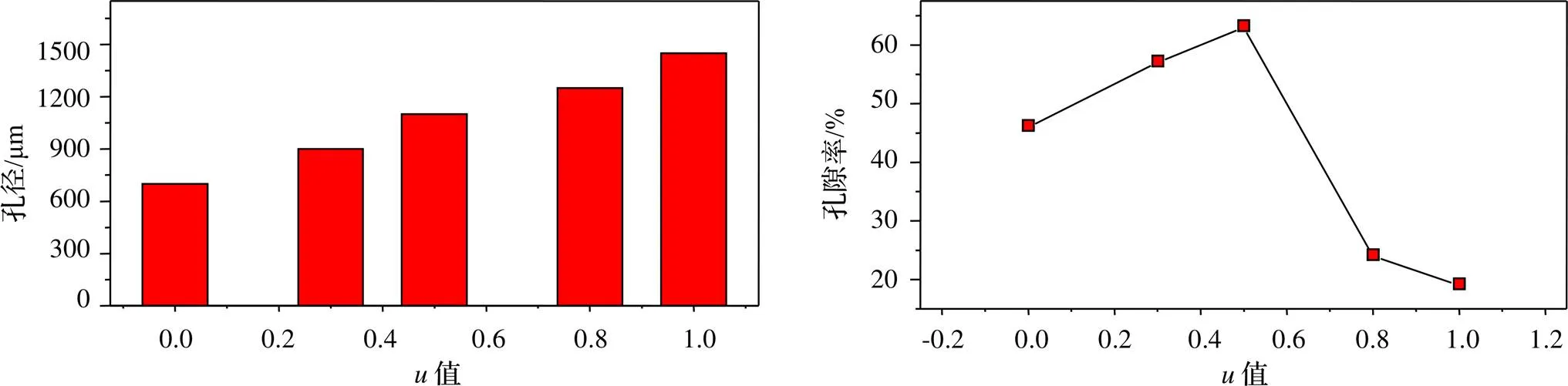
图3 u值对孔径及孔隙率的影响

从图3可以得出，如若将模型单元结构设计为表面封闭的实体结构，只有当参数值取为0.3及0.5时才能同时满足骨支架结构对孔径、孔隙率的基本要求，这无疑增加了支架模型设计的局限性，这时，可以换个思路，不将单元结构做成表面完全封闭的实体，而是将片状模型结构偏移一定的尺寸，这样即使当值选取0.8、0或者其他任意值时，改变偏移量也有可能可以获得合适孔径、孔隙率的模型结构。两种单元结构示意图如图4所示。

这两种单元结构的建模思想有一定的差异，无疑丰富了骨支架建模思路，但是对其更加具体的应用，还有待进一步探索。

在本文研究中，经过分析，取＝0.3，设计单元细胞结构尺寸为1.5×1.5×1.5 mm，将单元细胞结构设计为实体结构，并进行三个维度的阵列，依靠体与体之间的孔隙结构，同样能得到三维空间相互贯穿的多孔结构，并且这样得到的模型结构具有很好的力学性能，完全符合骨支架对力学性能的要求。

图4 两种不同的模型单元结构

图5为设计的整体模型结构，尺寸9×9×12 mm，整体孔隙率57%，孔径900 mm。

图5 u＝0.3时设计的整体结构模型

2 分析与讨论

本文设计的骨支架结构，假定应用在人体胫骨缺损部分治疗。用ANSYS软件进行力学仿真分析，由于钛合金材料具有强度高、耐腐蚀性好、耐热性高，并且与人体组织的生物相容性良好，不会发生排异、过敏反应，也没有毒副作用，对任何植物动物细胞都不会产生危害，于是被广泛应用于高端医疗领域，因此，赋予仿生多孔骨支架钛合金（Ti6Al4V）的材料属性。自定义添加钛合金材料属性为密度4620 kg/m3、杨氏模量110 GPa、泊松比0.3，为简化运算，选取2×2的单元结构进行仿真分析。

正常人体胫骨骨组织横截面积为176.25 cm2，人体运动时胫骨骨组织最高会承受体重的3倍重量[19-20]，所以对于体重为70 kg的正常人，胫骨骨组织垂直压力为0.117 MPa，由于植入体的固定方式为骨水泥固定、无相对位移，所以对支架下底面施加固定约束，并施加表面受垂直于下底面的压力。毫无疑问，骨支架植入人体后，垂直于支架表面的力为最大作用力，设计的模型结构是否满足植入的力学要求，也重点考虑垂直于模型的受力方向。将模型导入ANSYS软件，运用系统默认方式划分网格，选取整个底面添加固定约束，对整个上表面添加垂直作用力，如图6所示。

垂直向下的力＝0.117 MPa，支架模型的等效应力分布如图7所示。其等效应力分析结果表明，支架模型所受的等效应力大部分分布在0.26266 MPa以下。较大的等效应力主要集中在孔隙交接处，大小为2.02447e-9～0.26266 MPa。利用激光熔化加工的钛合金的屈服强度在1064 MPa，模型的最大等效应力为0.26266 MPa，远远小于钛合金屈服强度，所以满足屈服强度的要求[21-22]。

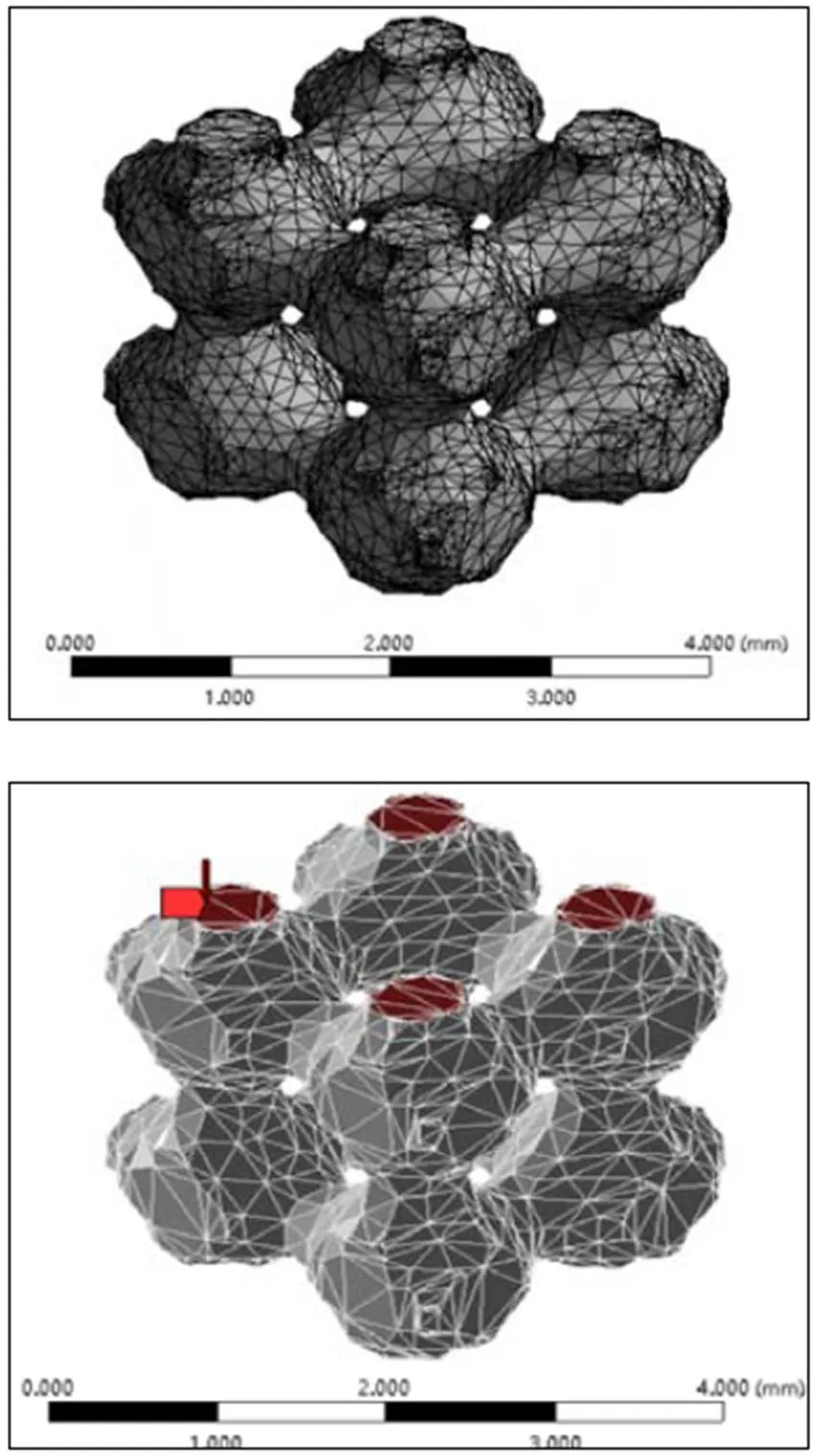
图6 模型网格划分及表面作用力图

图7 模型等效应力云图

支架模型总变形量的计算结果如图8所示，其总变形量的范围在0～1.6101e-6 mm，总变形量从上表面到下表面依次减小，且变形较大的地方为孔隙交接处。总变形量的最大值为1.6101e-6 mm，符合组织工程学对植入物的要求[23]。

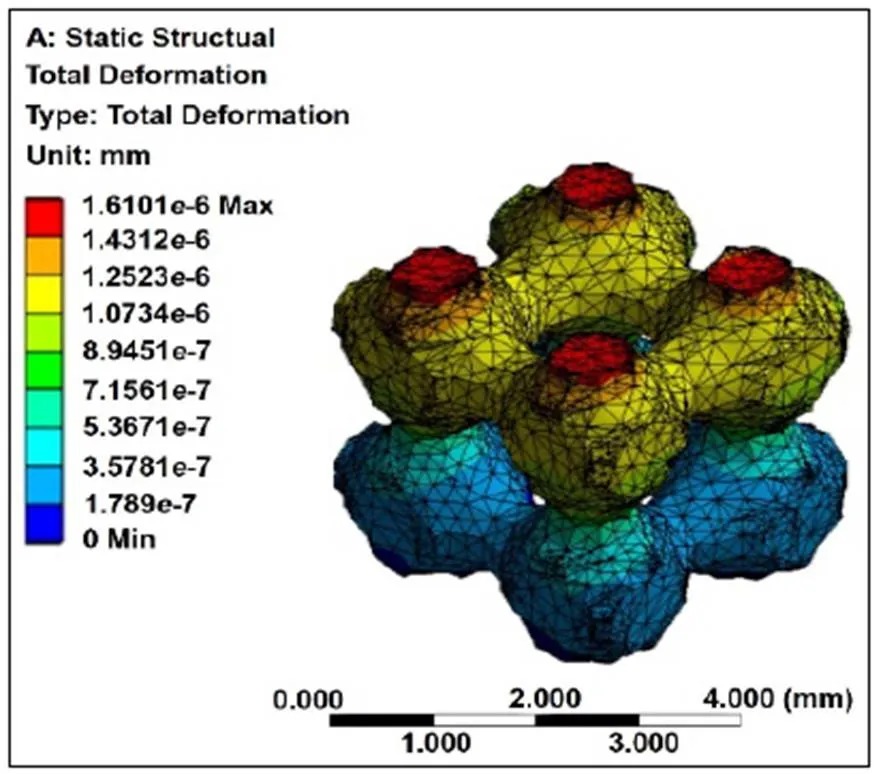
图8 模型总变形云图

3 结论

本文研究的目的是通过TPMS方法进行仿骨支架的建模，得到匹配人体真实骨性能的支架结构。通过查阅相关资料[24-25]，得出适合骨细胞附着增殖生长的孔径、孔隙率，于是，在进行仿骨支架结构设计时，通过改变函数参数，使模型的孔结构满足这些条件，通过相关计算，得出当＝0.3时，P曲面结构满足孔隙结构要求，并且具有优越的力学性能。后续通过ANSYS进行力学仿真分析，验证结果表明，设计的支架结构，力学性能优良，毫无疑问能够满足骨组织对骨支架结构力学性能的要求。

然而，论文研究工作中还有一些局限性。主要为虽然孔径、孔隙率满足细胞生存生长条件，并且钛合金材料制备的模型结构满足植入要求，但是并没有使用钛合金材料将模型制备出来，并进行确切的细胞增殖实验，得出细胞生长数据，弄清改变参数对细胞增殖生长的具体影响。所以下一步的重点工作是将模型运用3D打印成型技术、钛合金材料，将其制备出来，并进行细胞实验，考察一定周期内，细胞及组织生长状况，得出具体数据，方便后续对模型结构进行相关调整提供直观可靠的依据。

[1]Iyoda K，Miura T，Nogami H. Repair of bone defect with cultured chondrocytes bound to hydroxyapatite[J]. Clinical Orthopaedicsand Related Research，1993，288（288）：287-293.

[2]Burchardt H. Biology of bone transplantation[J]. Orthopedic Clinics of North America，1987，18（2）：187-196.

[3]Burg K J L，Porter S，Kellam J F. Biomaterial developments for bone tissue engineering[J]. Biomaterials，2000，21（23）：2347-2359.

[4]Meijer G J，de Bruijn J D，Koole R，et al. Cell-based bone tissue engineering[J]. Plos Medicine，2007，4（2）：260-264.

[5]Rezwan K，Chen Q Z，Blaker J J，et al. Biodegradable and bioactive porous polymer/inorganic composite scaffolds for bone tissue engineering[J]. Biomaterials，2006，27（18）：3413-3431.

[6]Yoshimoto H，Shin Y M，Terai H，et al. A biodegradable nanofiber scaffold by electrospinning and its potential for bone tissue engineering[J]. Biomaterials，2003，24（12）：2077-2082.

[7]乌日开西·艾依提，赵梦雅，等. 复合结构组织工程化人工骨的金属支架结构设计研究[J]. 新疆大学学报（自然科学版），2014，（4）：394-397，376.

[8]周俞. 基于骨组织微结构模型的仿生支架逆向设计[J]. 机械，2019，46（7）：1-5.

[9]Jung Y，Chu K T，Torquato S. A variational level set approach for surface area minimization of triply-periodic surfaces[J]. Journal of Computational Physics，2007，223（2）：711-730.

[10]Kapfer S C，Hyde S T，Mecke K，et al. Minimal surface scaffold designs for tissue engineering[J]. Biomaterials，2011，32（29）：6875-6882.

[11]Polthier K. Geometric data for triply periodic minimal surfaces in spaces of constant curvature[J]. Geometric Analysis and Computer Graphics，1991，17：139-145.

[12]Busse B，Hahn M，Niecke M，et al. Allocation of nonbirefringent wear debris: Darkfield illumination associated with PIXE microanalysis reveals cobalt deposition in mineralized bone matrix adjacent to CoCr implants[J]. Journal of Biomedical Materials Research Part A，2010，87A（2）：536-545.

[13]Newbury D E，Joy D C，Echlin P，et al. Advanced scanning electron microscopy and X-ray microanalysis[J]. Eos Archives，1986，35（69）：821-821.

[14]朱锐，沈霖，杨艳萍. 年龄、身高、体重、体重指数与武汉地区绝经后骨质疏松症患者骨密度的关系[J]. 中华骨质疏松和骨矿盐疾病杂志，2010，3（4）：234-238.

[15]Ki C S，Park S Y，Kim H J，et al. Development of 3-D nanofibrous fibroin scaffold with high porosity by electrospinning: implications for bone regeneration[J]. Biotechnology Letters，2008，30（3）：405-410.

[16]Lin C Y，Kikuchi N，Hollister S J. A novel method for biomaterial scaffold internal architecture design to match bone elastic properties with desired porosity[J]. Journal of Biomechanics，2004，37（5）：623-636.

[17]BegumSR，ArumaikkannuG. Design, analysis and fabrication of customised bone scaffold using RP technology[J]. International Journal of Computer Applications in Technology，2013，47（47）：364-369.

[18]Petrie AroninCE，Sadik K W，Lay A L，et al. Comparative effects of scaffold pore size, pore volume, and total void volume on cranial bone healing patterns using microsphere-based scaffolds[J]. Journal of Biomedical Materials Research Part A，2010，89A（3）：632-641.

[19]Ebrahimi H，Rabinovich M，Vuleta V，et al. Biomechanical properties of an intact， injured， repaired， and healed femur： an experimental and computational study[J]. Journal of the Mechanical Behavior of Biomedical Materials，2012（16）：121-135.

[20]姜海波，葛世荣. 基于CT扫描人体股骨的有限元分析[J]. 工程力学，2007，24（10）：156-159.

[21]Szpalski M，Gunzburg R，Aebi M，et al. A new approach to prevent contralateral hip fracture： Evaluation of the effectiveness of a fracture preventing implant[J]. Clinical Biomechanics，2015，30（7）：713-719.

[22]Weinans H，HuiskesR，GrootenboerHJ. Quantitative analysis of bone reactions to relative motions at implant-bone interfaces[J]. Journal of Biomechanics，1993，26（11）：1271-1281.

[23]Foucher K C，Hurwitz D E，Wimmer M A. Relative importance of gait vs. joint positioning on hip contact forces after total hip replacement[J]. Journal of Orthopaedic Research，2010，27（12）：1576-1582.

[24]Berner, A，et al. Effects of scaffold architecture on cranial bone healing[J]. International Journal of Oral and Maxillofacial Surgery, 2014，43（4）：506-513.

[25]Hollister S J，et al. Engineering craniofacial scaffolds[J]. Orthodontic & Craniofacial Research，2005，8（3）：162-173.

The Bionic Bone Scaffold Structure Design Based on the Triply Periodic Minimal Surface Modeling Method

SHI Zhang’ao，ZHOU Xin

( School of Mechanical and Engineering, Sichuan University, Chengdu 610065, China )

In order to better fit the porous surface environment for the survival and growth of human bone cells, in this paper, a function of the triply periodic minimal surface modeling method (TPMS) is adopted to design the bionic bone scaffold structure. With this method, the pore size and porosity of the bionic bone scaffold can be precisely controlled by adjusting the relevant parameters of the function. In this paper, one of the TPMS structures, p-curved surface structure is selected. By comparing it with the pore size and porosity of the real bone structure unit of human body, the parameter valueof p-curved surface structure is selected, and the reasonable unit size of the bionic bone scaffold is determined. Finally, the mechanical analysis and evaluation of the model are carried out by finite element simulation software. The result shows that the designed scaffold structure can better match the mechanical properties of human bone structure, which is of great significance for the construction of artificial bone scaffold structure.

TPMS；artificial bone scaffold；finite element analysis

R687.4

A

10.3969/j.issn.1006-0316.2020.03.001

1006－0316 (2020) 03－0001－06

2019－10－12

国家重点研发计划（2016YFC1100600）；国家自然科学基金（61540006）

石张傲（1992－），男，安徽安庆人，硕士研究生，主要研究方向为骨组织工程。