能量法结合径向条分法求边坡稳定性
2020-04-10莫智豪刘保东朱剑宏饶平平
莫智豪,刘保东,朱剑宏,饶平平
(1.上海理工大学 环境与建筑学院,上海 200093;2.南宁城建管廊建设投资有限公司,南宁 530219;3.广西路桥工程集团有限公司,南宁 530011)
边坡是一种自然地质体,在受到外界因素影响时,边坡土体会沿着一些不稳定的结构面滑动,导致边坡的失稳。边坡稳定性分析是岩土工程的重要研究内容,已经形成一个应用研究课题,其稳定性问题涉及采矿工程、水利和水电工程等许多工程领域,近年来受到越来越多的关注。边坡稳定性分析方法有很多种,其中基于定性判断的工程地质分析方法得到广泛应用,还有基于刚性定量计算的极限平衡法和基于数值计算的强度折减法[1-2]。工程地质分析方法主要分析了边坡的成因历史,研究了边坡所处的地质环境、形成的地质历史,以及影响边坡稳定性的变形破坏轨迹之间的关系,从而对其稳定状况作出宏观评价[3]。极限平衡法基于Mohr-Coulomb 屈服准则和静力平衡,根据边坡潜在破坏面上抗滑力与滑动力的比值来确定边坡稳定系数,然后合理评估斜坡的稳定性[4]。强度折减法是有限元中引入的计算安全系数的方法,通过对边坡土体参数进行折减,使边坡达到最终的极限平衡状态,根据该方法可以得到安全系数和潜在破坏面的位置[5]。
以上的边坡稳定性分析方法均在工程上有广泛的应用,且获得了工程界的认可,但各自均存在明显的不足。工程地质法类比条件因地而异,经验性强,没有数量界限,需要具有丰富的工程实践经验的地质工作者才能作出较为准确的判断。通过极限平衡法难以确定破坏面的形状和位置,这给边坡的稳定性分析带来了很大的困难。此外,极限平衡法没有考虑土的应力-应变关系,计算的土体条间力或滑块底部的反作用力不能代表滑坡滑动时的真实力,这给边坡稳定性分析带来了很大的不确定性,无法判断边坡的变形破坏模式。在强度折减法中,降低岩土强度参数c和φ的方法缺乏理论依据,并且以相同的比例减小,还是以不同的比例折减等问题仍缺乏合理依据,但目前还是得到了广泛的应用与认可。
本文使用的能量法从极限分析的上限定理演化而来。极限分析方法最初由Drucker 等[6]提出,为斜坡的稳定性分析开辟了一条新的道路。Chen[7]首次讨论了岩土结构的稳定性分析,并讨论了极限分析在岩土边坡稳定性中的应用。Michalowski[8-9]使用楔形体和竖直条块平动破坏机构以及转动机构对边坡进行了上限分析。王根龙等[10-12]采用塑性极限分析法结合条分法和等分圆弧面法对土坡进行了分析。赵炼恒[13]、陈静瑜等[14]基于极限分析上限定理,考虑孔隙水压力的影响,提出折线形滑面边坡稳定性计算模型。易庆林等[15]根据虚拟滑动位移,结合地下水的影响,提出滑坡稳定性计算模型。
本文从能量守恒的角度出发,建立了边坡稳定性计算模型。针对滑动面为对数螺旋面的边坡,采用径向条分法,虚设虚拟转角位移,考虑块体间相对位移产生的内部耗能,计算滑坡重力势能和滑面摩擦内能的变化,使用强度折减法计算边坡稳定性。
1 基本原理和物理模型
1.1 基本原理
利用滑坡体和滑动面作为能量守恒法判断边坡稳定状态的研究系统。假设滑动面上的土体沿对数螺旋滑动面的极点O产生非常小的角位移dθ,将其称为虚拟转角位移。在此过程中,重力势能的变化量为ΔU,抗滑力(滑动面上黏聚阻力与滑动摩擦力)做功ΔW1,块体分界面上由于土体自适应变形而相对运动产生的内能耗散(黏聚阻力所做的功)为ΔW2。
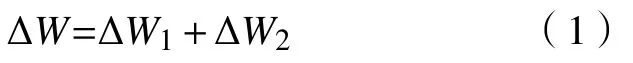
采用强度折减法[16]对土体参数c和φ进行折减,安全系数为
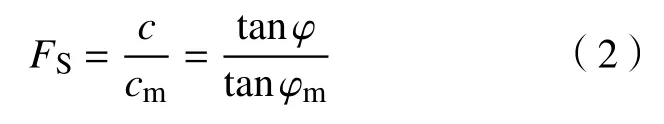
式中:c,tanφ为实际土体强度参数;cm,tanφm为维持边坡稳定的极限强度参数。土体参数折减后边坡达到极限平衡状态,即

1.2 物理概化模型
本文所研究的边坡稳定性计算物理模型如图1所示。图中:滑动面处于对数螺旋曲线AB上;点O是对数螺旋线的极点;点A是破坏面与边坡上部平面的交点;点B为坡脚位置;θA和θB分别为A点和B点对应的角度;r0为A点所对应的初始极径;H为边坡高度;α为坡角。假设边坡土体服从相关联流动法则和Mohr-Coulomb 屈服准则的理想塑性变形假设,根据Chen[7]所述,采用对数螺旋面作为边坡的滑动面。
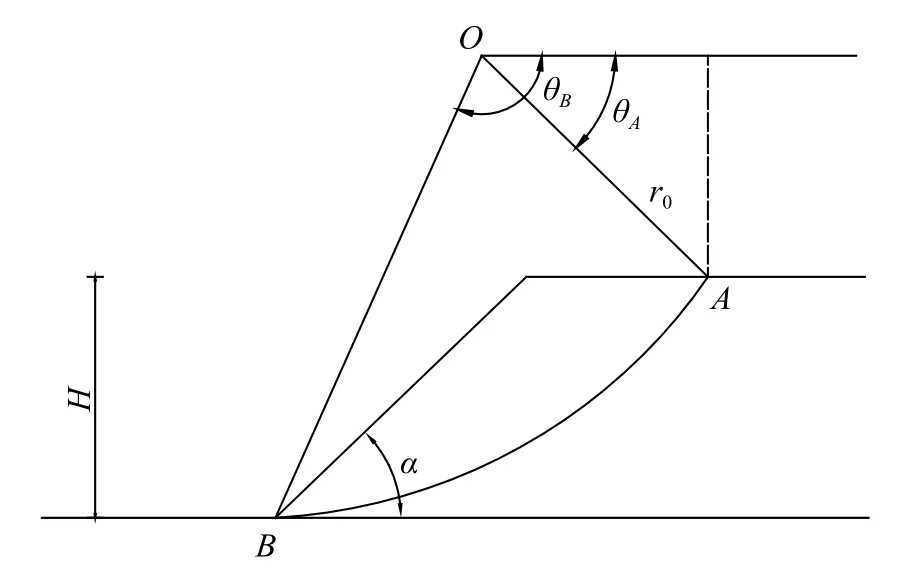
图1 边坡模型Fig.1 Slope model
对数螺旋滑动面曲线方程为
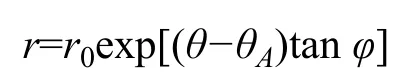
根据极限分析上限法的原理和许多大型滑坡的运动特征研究,土体在运动过程中,下部土体的运动速度通常大于上部土体的运动速度,在此基础上,如果仍然采用垂直条分法或斜条分法显然不合适。本文采用径向条分法研究滑动面上的土体,即从极点O中提取出一系列射线,将滑动面上的土体根据角度等分成n个小滑块,每个小块所占角度,如图2 所示。
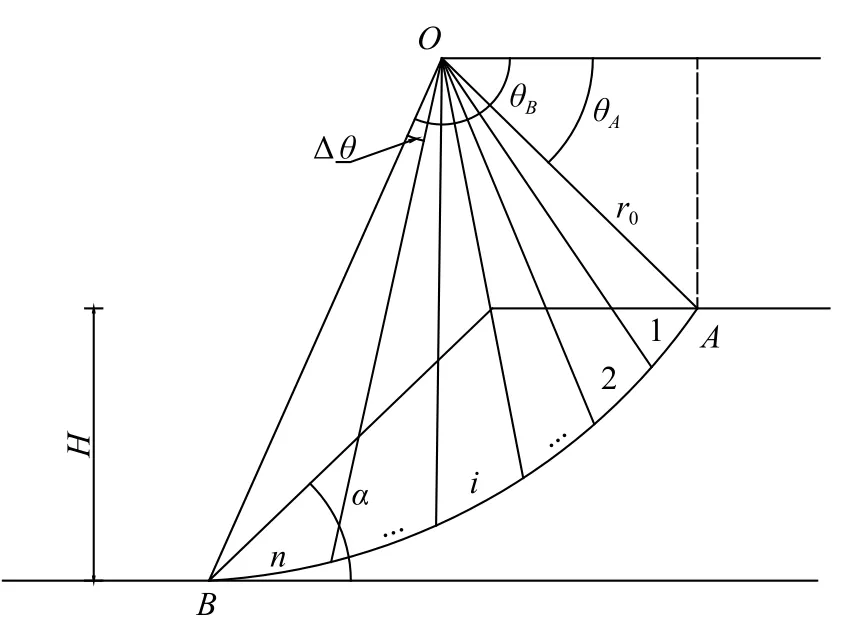
图2 径向条分后的边坡模型Fig.2 Slope model after radial slicing
本文对能量法边坡稳定性计算模型进行了以下简化假设:a.假设各块体为刚体;b.所研究的边坡滑动面为对数螺旋滑动面;c.边坡在产生虚拟转角位移dθ的过程中,由于自适应变形各块体间产生相对运动;d.不考虑相邻块体间土体自重所产生的摩擦耗能。
2 稳定性计算模型
2.1 重力势能改变量
如图2 所示,采用径向条分法将边坡对数螺旋滑动面上部的土体根据极角等分为n个块体。根据块体重心的变化来计算块体重力做功,对于扇形结构其重心在其角平分线上,所以分析中取块体中线进行计算。假设每个块体的重心位于块体中心线(块体对应角度的角平分线)的中点,第i个块体的质量为Gi。当某一时刻产生虚拟转角位移dθ时,第i个滑块的重心的位移为dSi,其对应的竖向位移为dyi,则重力势能改变量为
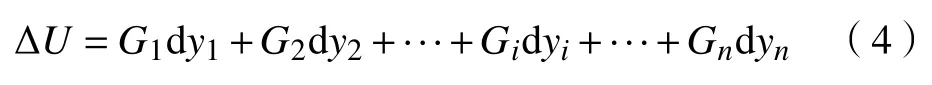
将图形简化为如图3 所示,计算第i个块体的重力势能改变量。∠QOA=θA,第i个块体重心线与水平线OQ之间的夹角为位移后新重心线与水平线OQ之间的角度为
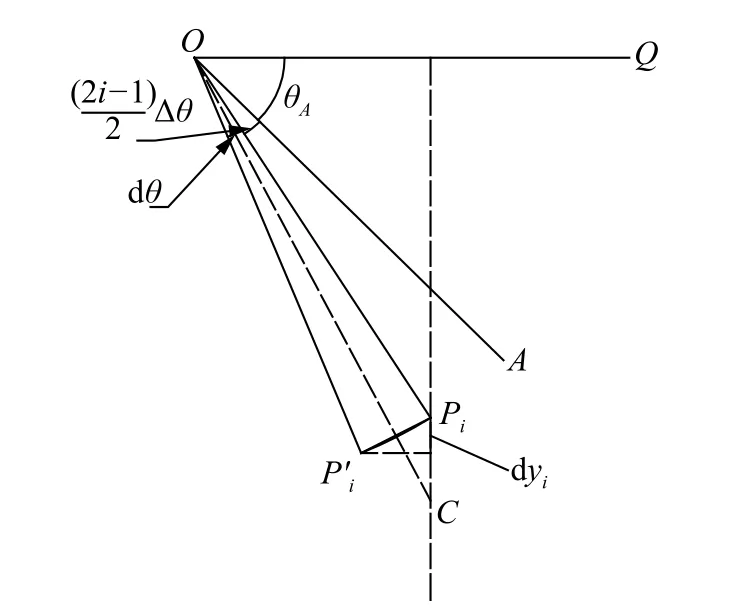
图3 滑块的重心位移示意图Fig.3 Sketch of slider center under gravity changes
设初始重心Pi到极点O的长度为′,在转动角度dθ后,Pi与之间的距离为
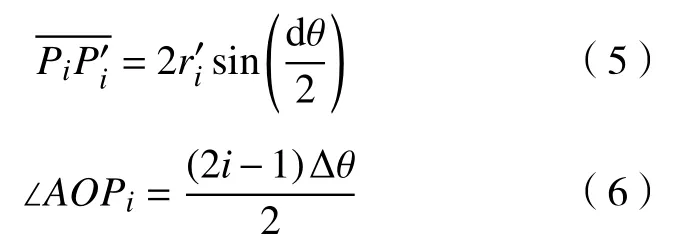
转动的角度为dθ,由图中几何关系可知:
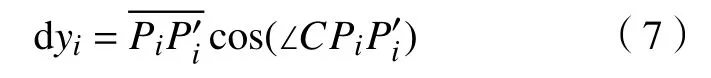
其中
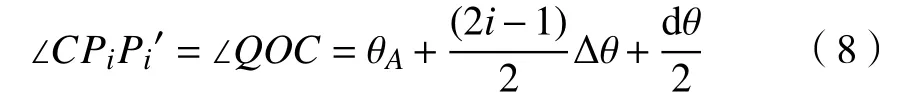
所以

2.2 滑动面抗滑力做功
由于滑动面上部土体产生位移,且存在黏聚力和滑动摩擦力,则滑动面上会产生能量耗散。
a.滑动摩擦力做功

式中,F为滑块自重在滑动面上的法向分力与摩擦系数μ的乘积,dsi=ridθ,r为滑块中线的长度。
b.黏聚力做功

式中,c为土体的黏聚力,Δs=riΔθ(当n足够大时,滑块在滑动面上的部分可近似为圆弧形曲线)。
对第i个块体进行计算,如图4 所示。
对其运动几何图进行分析,如图5 所示。
由几何关系可得
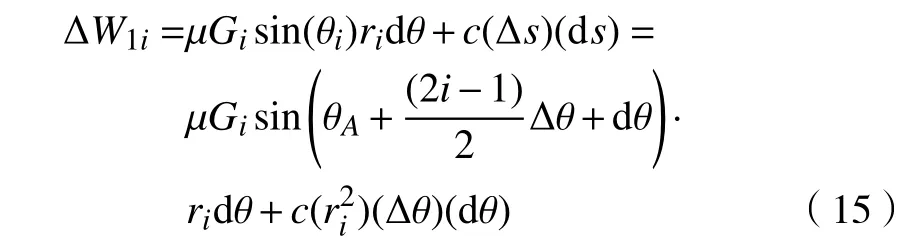
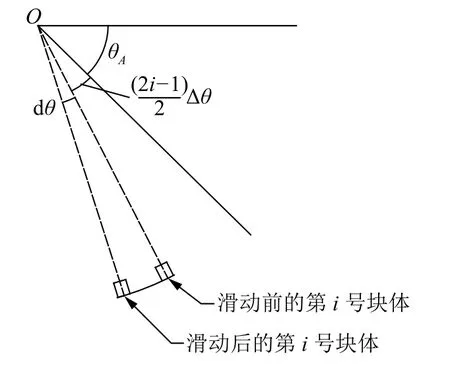
图4 滑动面上内能耗散示意图Fig.4 Energy dissipation on the sliding surface
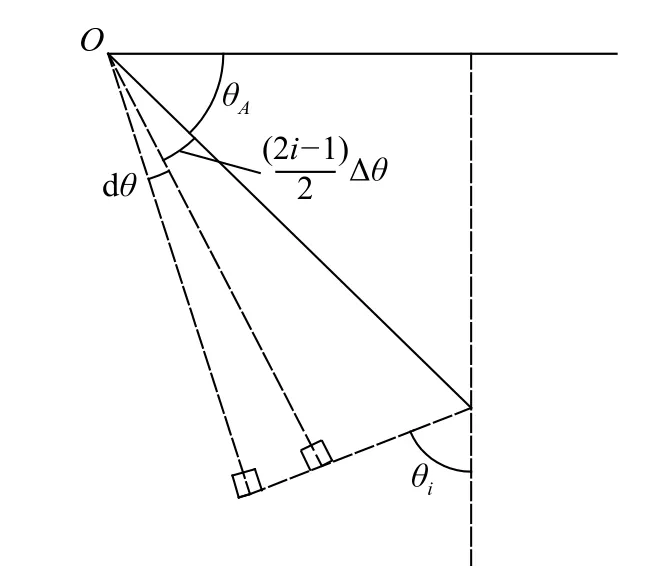
图5 滑块摩擦耗能计算几何分解图Fig.5 Geometric diagram of the calculated energy dissipation due to slider friction

2.3 相邻块体接触面上的能量耗散
由于采用对数螺旋滑动面,其上部土体会产生变形,块体间会产生能量耗散,如图6 所示。
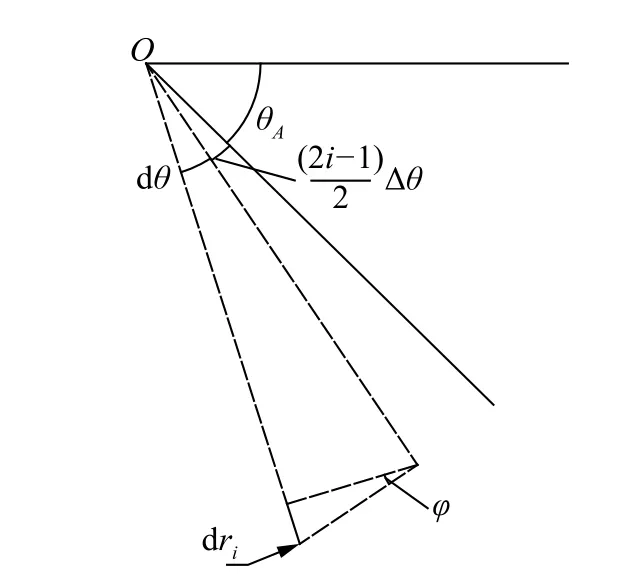
图6 块体径向位移Fig.6 Radial displacement of the slider
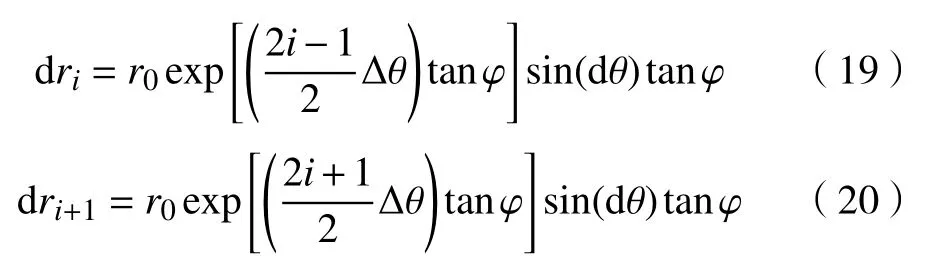
所以第i个块体与第i+1 个块体接触面相对位移
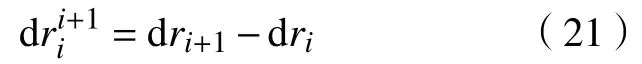
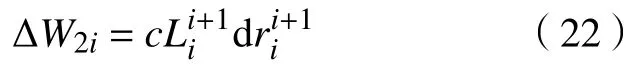
由于n个块体间存在n-1 个接触面,所以
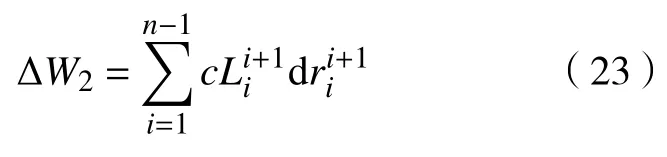
3 算例分析
3.1 算例概况
为了说明本文的合理性,采用工程算例进行验证。如图7 所示边坡,设边坡土体均质且服从Mohr-Coulomb 屈服准则,土坡高度H=20 m,坡角α=60°,土体重度γ=19 kN/m3,摩擦角φ=24°,黏聚力c=35 kPa。
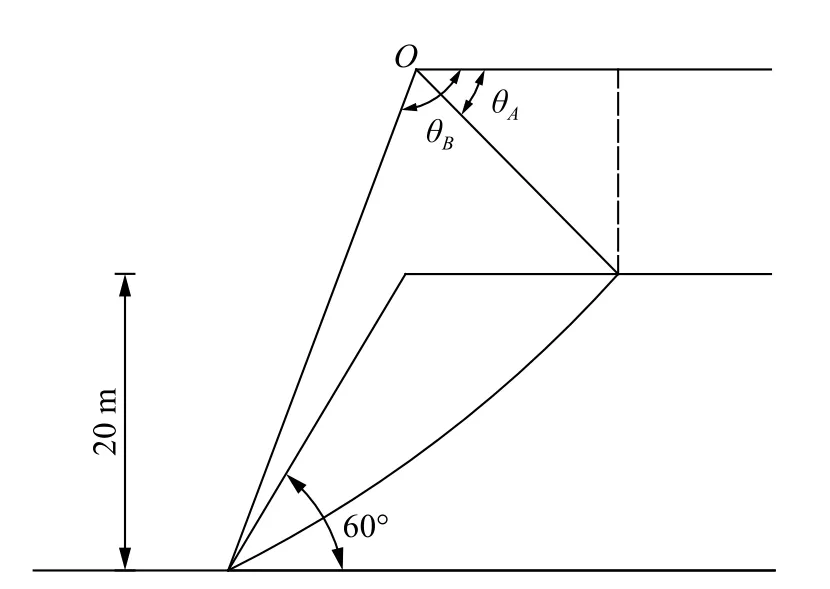
图7 稳定性计算模型Fig.7 Stability calculation model
3.2 计算方法
采用径向条分法,将对数螺旋滑动面上部土体根据角度等分为20 份,每份对应极角为(θA-θB)/20。假设虚拟转角位移dθ=0.01°。将推导出来的表达式使用Matlab 软件进行编程,使用fmincon优化程序对表达式中的变量θA和θB进行优化,得到最小安全系数FS,根据其对应的参数θA和θB即可得到最危险滑动面。
3.3 计算结果
通过本文介绍的能量法,计算求得稳定性系数FS=1.228。使用极限分析法对该算例进行建模和计算,得出稳定性系数FS=1.240,能量法和极限分析法的计算结果之间的差异为0.97%。通过本文方法得到的计算结果与常用的边坡稳定性极限分析方法获得的结果差别不大且更加准确,说明了本文方法的正确性,对边坡的稳定性评估及设计施工有一定的参考价值。
4 参数影响分析
对于给定的边坡模型,不同的参数对计算结果有很大的影响。基于算例1 中的边坡稳定性计算模型,分析了条块数n、虚拟转角位移dθ、黏聚力c、摩擦角φ和坡角α对稳定系数的影响,并将计算结果与极限分析上限法得出的结果进行了对比分析。
4.1 条块数n 对稳定系数的影响
从理论上来说,将滑动土体进行分块,考虑其块体间摩擦耗能,是对计算结果的进一步优化,且条块数n取值越大,结果越精确。对算例1 中的边坡稳定性计算模型,分别取条块数n为5,10,15,20,25,30,模型中其他参数不变,计算边坡稳定性系数,其计算结果如图8 所示。从图中可知,随着条块数n的增大,边坡稳定性系数FS逐渐减小,且当n大于一定值后,边坡稳定性系数FS趋向于收敛。由于计算过程比较复杂,因此在后面的例子中,模型的径向条块数均为20。
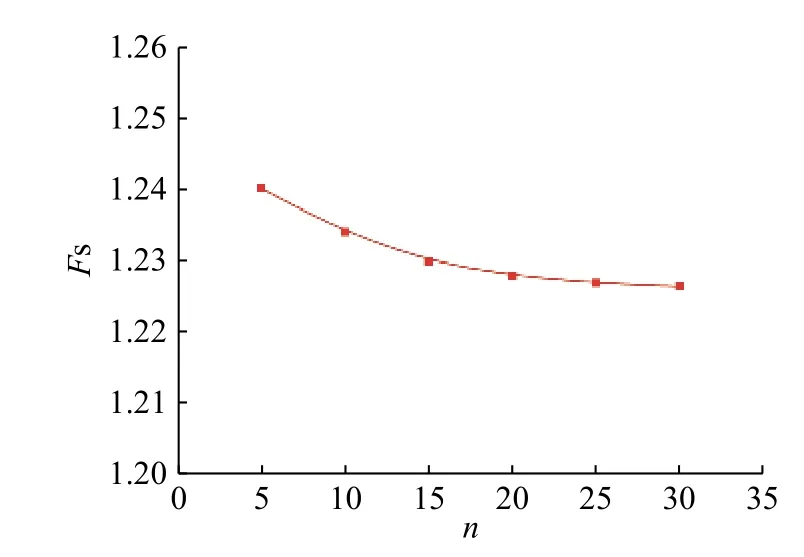
图8 条块数对稳定系数的影响Fig.8 Influence of number of slider blocks on the stability factor
4.2 虚拟转角位移dθ 对稳定系数的影响
从理论上来说,虚拟转角位移dθ数值越小,计算结果越精确。采用算例1 中的计算模型,令dθ取值0.001°,0.01°,0.1°,1°,10°,且其他参数保持不变,计算边坡稳定性,结果如图9 所示。从计算结果可以看出,在一定范围内,dθ取值越小,边坡稳定性系数FS越小,但当dθ小于某一数量级后,FS基本上趋于稳定。根据上述计算所得的结果,当dθ<0.1°后FS值基本趋于稳定,所以后面的算例中均按照dθ=0.01°进行计算。
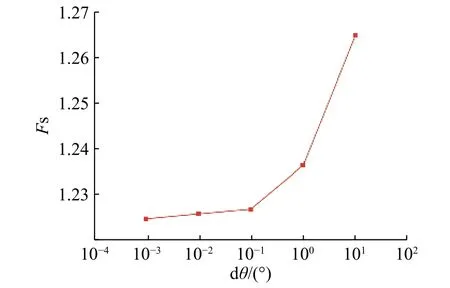
图9 转角位移对稳定系数的影响Fig.9 Influence of virtual displacement on the stability factor
4.3 物理参数c,φ,α 对稳定系数的影响
采用算例中的数据,分别对c,φ,α取不同值计算稳定性系数,并与极限分析法的计算结果进行了对比分析。如图10~12 所示。

图10 黏聚力对稳定系数的影响Fig.10 Influence of cohesive force on the stability factor
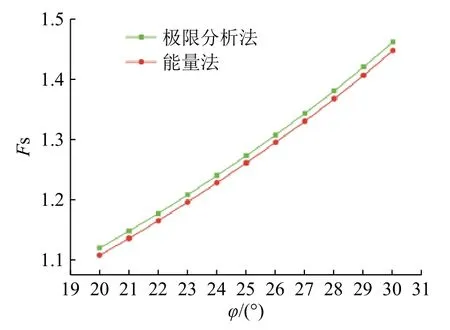
图11 内摩擦角对稳定系数的影响Fig.11 Influence of friction angel on the stability factor
根据图10 中的曲线,能量法与极限分析法计算出来的稳定系数相差不大,但能量法计算出来的结果更小。其变化规律基本一致,稳定系数随着c值的增大而增大。根据图11 中的曲线,边坡稳定系数随着土体内摩擦角φ值的增大而增大,但能量法的计算结果要小于极限分析法的计算结果。根据图12 中的曲线,能量法与极限分析法稳定系数均随坡角的增大而减小,且其减小规律基本一致,但能量法的计算结果更优。
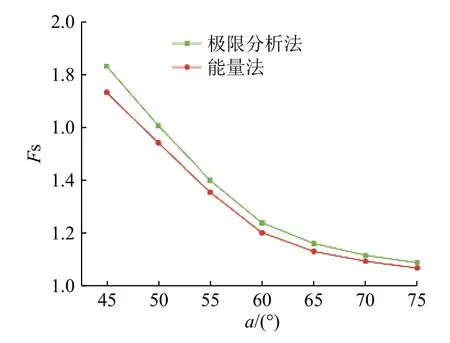
图12 坡角对稳定系数的影响Fig.12 Influence of slope angel on the stability factor
4.4 能量法与极限分析法的对比
本文的能量法与极限分析法有很多异同点。相同点是两者滑动面均为对数螺旋滑动面,且将滑动面上部划分的土体视为刚性块体。不同点主要在于建模方法的不同,在建立边坡物理计算模型过程中,能量法采用径向条分法。从极点引出一系列射线,将滑动面上部土体划分为若干径向条块,考虑块体与块体间的能量损耗,使安全系数更为精确。
从本质上来讲,极限分析法是通过构建虚拟速度场,从功率的角度来求解稳定系数,而能量法是假设虚拟角度,从能量的变化角度来求解。上述两种方法都是考虑滑块体的重力和滑动面上的抗滑力来进行计算,故而两种方法的计算结果应该是较为接近的。不同的是能量法通过虚拟转角位移dθ,计算力与位移的乘积,位移前后边坡状态不同。极限分析法通过虚设角速度ω,计算内外做功功率,边坡状态未发生变化。
5 结论
本文根据边坡失稳破坏过程中土体的运动模式,采用径向条分法和对数螺旋滑动面建立物理模型,虚设滑动面上部土体转角位移,采用能量法对边坡的稳定性进行计算,总结出以下几点:
a.通过建立能量法边坡稳定模型,考虑相邻块体间的能量损耗,推导出滑动土体重力做功公式ΔU、滑动面上内能耗散公式ΔW1以及各块体间的内能耗散公式ΔW2。结合强度折减法,计算边坡稳定系数FS。通过算例计算,并与极限分析法的计算结果进行对比验证。结果表明考虑内部能量耗散的能量法计算结果比极限分析法计算结果更优。
b.通过采用不同的土体参数与边坡几何参数,运用能量法与极限分析法分别计算稳定性系数,对比分析了各参数对边坡稳定性系数的影响规律,可为工程实践以及设计施工提供参考。
c.采用能量法计算边坡稳定性时,条块数n越大,计算结果越精确,虚拟转角位移dθ越小,计算结果越精确,边坡安全系数随着内黏聚力与内摩擦角增大而增大,随着坡角的增大而减小。
d.本文分析结果对工程实践有一定参考价值,但也存在不足。本文所研究的滑动面为对数螺旋滑动面,但实际中滑动面更为复杂。在计算块体间摩擦耗能时,只考虑了土体黏聚力的影响,未考虑各块体内部土压力造成的内能耗散。
