融合Spearman 相关性系数与多尺度框架的立体匹配算法

于修成，宋 燕，胡浍冕

（上海理工大学 光电信息与计算机工程学院，上海 200093）

立体匹配是机器视觉领域的研究热点之一。通过查找从不同视角获取的同一场景的两张或多张图像之间的匹配像素点，得到匹配像素点之间的位移差（即视差）[1]，然后通过三角化可得到其3D 深度，进而估算出场景的3D 模型。立体匹配已经广泛应用于视觉导航、物体定位和三维重建等领域[2]。

立体匹配自诞生以来取得了长足的进步。Scharstein 等[3]总结立体匹配的发展，建立了一套完整的立体匹配评价体系，并提供了相应的测试数据集，同时指出立体匹配过程可分为4 个阶段：代价计算、代价聚合、视差选择与优化和视差强化。在代价计算阶段，通过在视差范围内计算像素间的匹配代价来得到空间代价图。在空间代价图中，由于匹配代价计算得到的匹配代价图包含较大噪声，因此，在代价聚合阶段需要通过以像素点为中心的支持窗口内的其他匹配代价来修正当前像素点的匹配代价，因此，隐含假设了代价聚合具有平滑特性[3]。根据视差计算和优化策略的不同，立体匹配可以分为局部立体匹配和全局立体匹配。在局部立体匹配中，使用WTA（winner takes all）算法，从视差空间图中取每个像素点的最小匹配代价对应的视差作为当前像素点视差。全局立体匹配算法通常在视差空间图中定义一个能量函数，包含数据项和平滑项[4]。其中，数据项就是视差空间图中的匹配代价，平滑项用来表征相邻像素之间的视差约束程度，然后通过最小化能量函数可以得到最终的视差图。在视差强化阶段，通常采用相关的算法，如左右一致性检验、空洞填充以及中值滤波[5]等对获得的视差图进行修正，以得到误匹配率更少、场景中物体轮廓信息保持更好的视差图。在以上的步骤中，代价计算和代价聚合对获取有效的视差图的作用很大，因此，本文着重研究这2 个步骤。

在代价计算中，通过匹配基元的不同，可以将代价计算方法分为两类：基于像素和基于窗口的方法。在匹配成本计算时，前者基于像素与像素间的匹配相似度，而后者计算支持窗口之间的相似度[6]。虽然基于像素的方法效率很高，但它们的匹配精度较低。随着研究进一步的深入，一些基于窗口的成本计算解决方案被引入到代价计算中。典型的算法包括绝对平方差，这些方法能够大大降低误匹配率[7]。然而，由于此类算法的特殊性，在某些特殊领域有很大的局限性，例如，低纹理以及重复纹理等。因此，随着研究的深入，一些基于非参数变化的方法，如rank 变换和census变换被引入到匹配代价计算中[8]。

在代价聚合中，大部分代价聚合算法都隐含假设了代价聚合具有平滑性，可以看成是在空间视差图上进行滤波[9]。最简单的代价聚合方法是使用固定窗口，如盒子滤波或者高斯滤波器。由于隐含的施加平滑度，此类算法易造成深度边缘模糊的问题[10]。随着研究的深入，一些边缘保留滤波器被引入代价聚合中，其中，比较经典的是双边滤波[11]和导向滤波[12]。双边滤波器的计算量与其采用的核窗口的大小有关，核窗口越大，则滤波器计算量也越大，要取得好的滤波效果往往需要采用大的核窗口。导向滤波器的计算量与核窗口的大小无关，计算量相比双边滤波器小。然而，以上聚合算法都是基于支持窗口内的聚合，从而忽略了窗口外的像素信息，通过此类算法得到的视差图还有待进一步完善。近年来基于图论的思想，Yang[13]将核窗口扩展到整张图像，提出了一种非局部成本聚合方法，即在最小生成树上对代价进行聚合，使得匹配精度和匹配效率进一步提高。在Yang 等的基础上，Yao 等[14]提出通过分段树来聚合代价的方法。这些基于整幅图像聚合代价的方法能比局部的滤波器取得更好的视差图。以上立体匹配代价聚合方法推动了立体匹配的发展，使得立体匹配的精度进一步提高，但目前存在一个问题：多数是在图像的最大分辨率下进行处理的，而人类视觉系统是在多尺度空间中进行辨识物体，受此启发，Zhang 等[15]在文献中首次将高斯金字塔变换多尺度分解方法用于立体匹配代价聚合阶段的处理，搭建了一个跨尺度的代价聚合框架，有效地提高了采用局部算法得到的匹配率。

基于以上分析，本文提出一种基于Spearman相关性系数的多尺度代价聚合算法。在代价计算阶段，通过简化Spearman 相关性系数得到两种衡量匹配代价的模型。在代价聚合阶段，从传统的原始单分辨率匹配扩展多尺度上的匹配，从而实现Spearman 相关性系数与多尺度框架的融合。该方法相比其他算法，匹配精度得到了进一步的提高。

1 研究方法

1.1 匹配代价计算

在本文中，假定视差图是由经过校正后的立体图像对经过匹配获得。匹配代价是用来衡量不同视觉拍摄的两幅或者多幅同一场景不同图像在视差范围内对应像素点间的相似性。代价计算可看成是一种函数映射：f:RW×H×3×RW×H×3→RW×H×L，其中，W，H分别表示图像的高和宽，3 代表图像颜色通道，L为最大视差。则对于立体图像对I，I′使用式（1）得到匹配代价图。

对于原图的一个像素点p(x,y)，其中，x，y表示像素坐标，在视差为l时的匹配代价记为标量C(p,l)。现有匹配代价方法一般通过两种基元来计算C(p,l)，分别为单像素基元和窗口基元。IG（intensity+gradient）算法是基于单像素基元，计算公式为

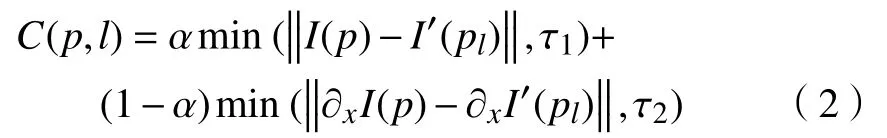
式中：I（p）表示图像I中像素点p的像素值；∂x表示x方向的像素梯度；τ1和τ2分别为像素和梯度的截断阈值参数；pl是右图中与p相差视差为l的图像坐标；α为调和参数。

常见的基于窗口基元的匹配代价计算方法包括rank 变换和Census 变换，这些都是基本的变换方法，在此不作阐述。

1.2 所提算法描述

Spearman 相关性系数用来衡量2 个相同大小序列的相关性。对于大小为n的序列X=(x1,x2,···,xn)，Y=(y1,y2,···,yn)，它们之间的Spearman 相关性系数可以用一个单调函数ρ(X,Y)表示。

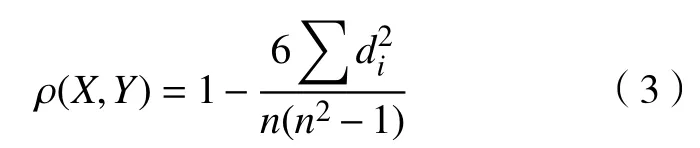
在立体匹配中，通常使用匹配代价来衡量匹配的程度，即匹配代价越小，则匹配的程度越高。因此，用最大值1 减去系数即可得到匹配代价。将以p和pl为中心的2 个支持窗口内像素集看作是2 个序列，则匹配代价可表示为

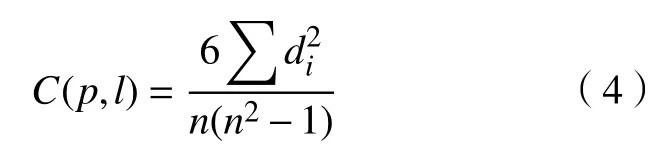
当进行代价匹配时，支持窗口大小一定，则n为常数，因此，对式（4）进一步等价可以得到最终的两种形式的匹配代价，即式（5）和式（6）。

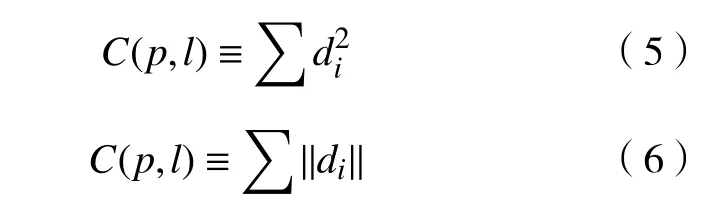
将式（5）和式（6）看作是基于Spearman 的代价匹配算法，即简化Spearman 的代价计算方法。由于该算法采用相关性作为匹配代价计算的基石，因此，其对光照干扰有较强的稳健性。但是，在低纹理和弱纹理等区域，其匹配代价还有待提高。在立体匹配中，大部分的局部算法都是在原始分辨率图像上进行匹配，这些方法能够取得较好的匹配效果，然而其在低纹理等区域的误匹配率高。考虑到人眼观察事物过程是一种由模糊到清晰的过程，因此，将Spearman 算法与多尺度框架进行融合，称此算法为Spearman 融合算法（SSpear），现介绍具体过程。

输入：立体彩色图像对I，I′。

a.建立高斯金字塔或者拉普拉斯金字塔Is，I′s，其中，s是金字塔的层数，s∈{0,1,···,S}；

b.在每一层中，通过式（5）或式（6）得到初始匹配代价图Cs；

d.通过以下公式得到最终的匹配代价

式中：A为(S+1)×(S+1)的系数矩阵；为第0 层的聚合后的匹配代价。

输出：基于原始尺寸图像的匹配代价。

最终通过WTA（winner takes all）算法得到最终的视差图。

2 实验结果与分析

使用Middlebury 立体匹配评估平台[16]对所提算法以及相关算法进行评估。Middlebury 数据集有2 个版本，分别为Middlebury 2.0 和Middlebury 3.0。2.0 版本共有31 个立体声对，记为M31。与2.0 版本相比，3.0 包含更复杂的场景。它提供了30 个立体图像对，分别为测试集和训练集，每个图像集有15 个图像对。在实验中仅使用训练集，表示为M15。使用误匹配像素的百分率（即绝对视差误差大于阈值的像素）作为评估标准。考虑到2 个数据集的分辨率，在M31 使用1 作为阈值，在M15使用2 作为阈值。实验主要由两部分组成：一种是在没有成本聚合的情况下，比较由各种匹配成本计算的视差图，包括Spearman 算法和融合方法S-Spear；另一种是比较相同成本聚合下匹配成本方法的匹配效果。

2.1 无代价聚合下匹配代价计算实验

选择基于梯度变换（GRD）、Census 变换、基于Spearman 算法（Spear）以及多尺度Spearman 算法（S-Spear）作为实验测试对象，在没有代价聚合方法的作用下，比较各种算法的性能。选择Middlebury 数据集中的M31 和M15 作为测试数据，以图像中非遮挡区域的匹配率（Non-occ）和全部图像的匹配率（all）作为测试算法性能的指标。数据集M31 和M15 所得测试数据如表1 和表2 所示。数据集M31 中立体图像对Venus 所得的实验结果如图1 所示。

表1 和表2 的结果表明，在数据集M31 所得数据中，所提Spear 算法和S-Spear 算法未经视差强化时在非遮挡区域的平均误匹配率（Avg-non）为13.76%和11.29%，所有区域的平均误匹配率（Avg-all）为26.43%和24.34%。在数据集M15 中，误匹配率分别为25.55%，23.32%，33.85%和30.96%。相比其他代价算法，所提Spearman 算法和多尺度Spearman 算法的误匹配率进一步降低。

表1 在数据集M31 上各代价计算方法所得测试结果Tab.1 Results of the cost computation methods on M31%

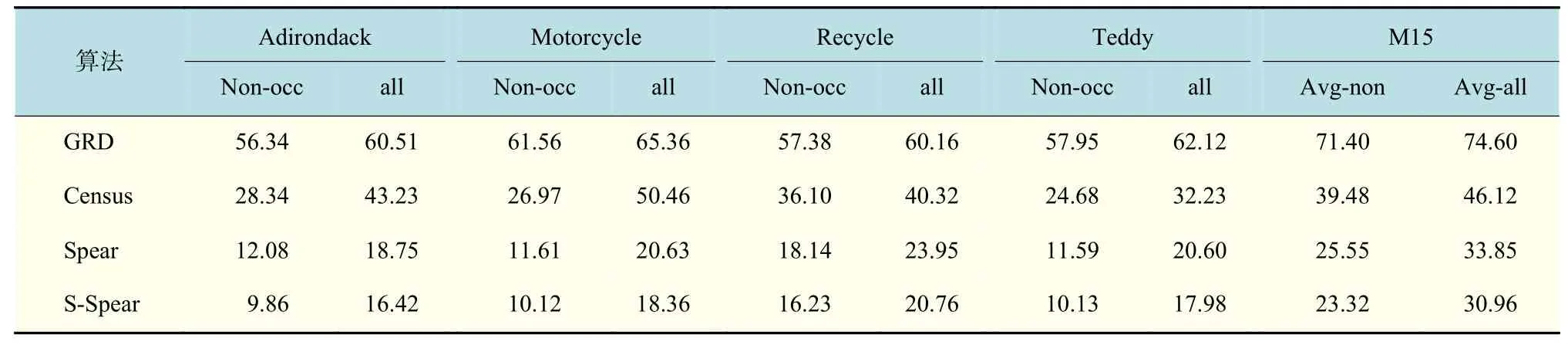
表2 在数据集M15 上各代价计算方法所得测试结果Tab.2 Results of the cost computation methods on M15%

图1 不同匹配代价算法所得的Venus 图像对的视差图Fig.1 Disparity maps of the Venus image pair for all cost computaion methods（without disparity refinement processing）

几种代价方法与所提Spear 算法和S-Spear 算法的视差图对比如图1 所示，可以看出，所提Spear 算法与S-Spear 算法的视差图中红色标记点（误匹配点）明显少于其他算法，在低纹理区域尤为明显。图1（e）中误匹配点明显少于图1（c），说明基于Spearman 算法的性能要优于GRD 算法，原因是基于Spearman 算法是基于窗口的匹配算法，在匹配精度上要优于GRD 算法。图1（e）中误匹配点明显少于图1（d），在低纹理区域尤为明显，说明基于Spearman 算法性能优于Census 算法，原因是基于Spearman 算法的是衡量窗口之间的相关性，而Census 算法则是简单地通过非参数变换得到最终的匹配代价。图1（f）中误匹配点要少于图1（e），由于增加了尺度因子，其在各个尺度进行了代价聚合，因此，多尺度的Spearman 算法要优于Spearman 算法。因此，所提算法在没有代价聚合时均表现出较好的匹配性能。

2.2 有代价聚合下匹配代价计算实验

在相同的代价聚合算法下，比较不同代价计算方法的性能。表3～5 分别为采用盒子滤波、导向滤波和最小生成树进行代价聚合得到的实验数据。图2 和图3 显示了融合最小生成树进行代价聚合时，数据集M15 中的Motorcycle 和Teddy 图像对所得的视差图结果。

表3～5 的中结果表明，无论是在盒子滤波、导向滤波还是在最小生成树滤波下，所提算法的误匹配率都要比其他代价计算方法低。如在最小生成树聚合的作用下，所提Spearman 算法和多尺度Spearman 算法在数据集M31 中非遮挡区域的平均误匹配率为8.26%和7.98%，所有区域的平均误匹配率为19.37%和18.26%，匹配效果进一步增强。图3 展示了M15数据集中Motorcycle 图像对所得的视差图，3（e）和3（f）是基于所提Spearman相关性系数和融合多尺度框架得到的视差结果图，其视差效果要明显好于GRD 和Census 算法得到的视差图（图3（c）和3（f）），从图中可以明显看出所提算法得到的视差图更接近真实视差图。

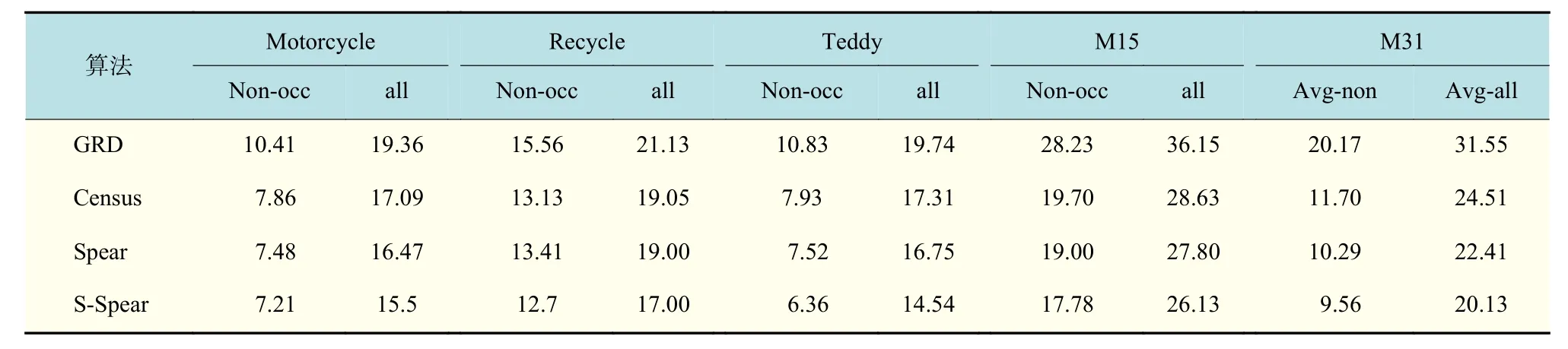
表3 盒子滤波作用下各匹配代价所得测试结果Tab.3 Results of the cost computation methods with box filter aggregation%

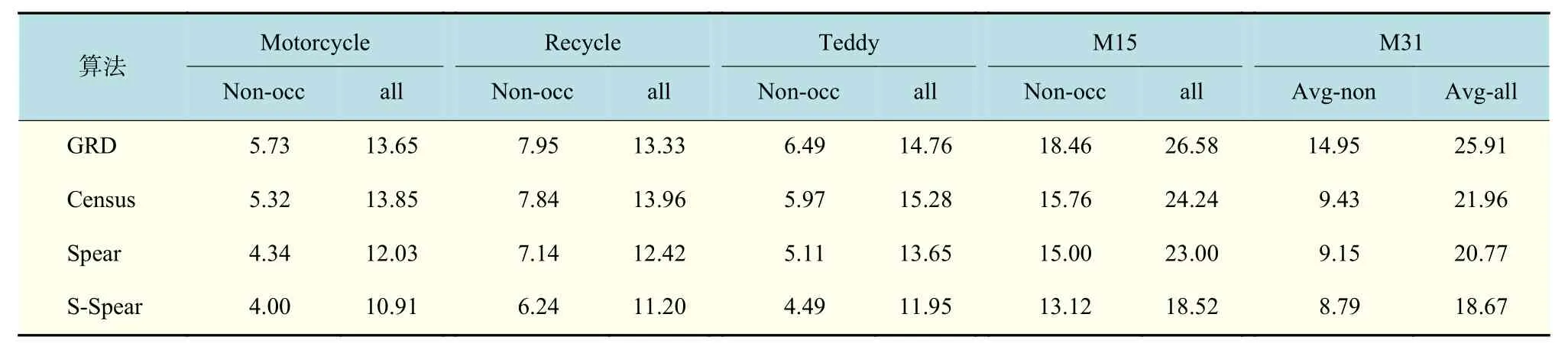
表4 导向滤波作用下各匹配代价所得测试结果Tab.4 Results of the cost computation methods with guide filter aggregation%

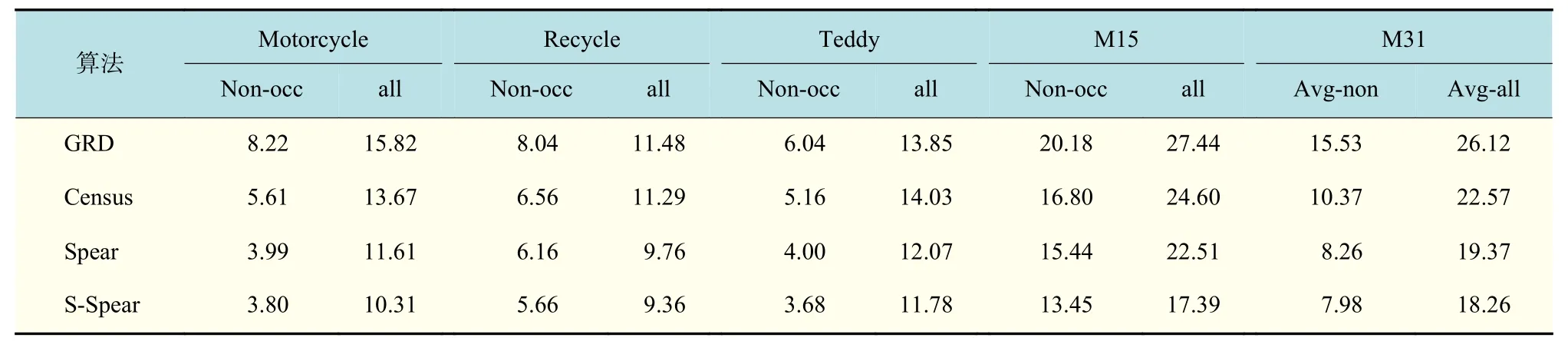
表5 最小生成树作用下各匹配代价所得测试结果Tab.5 Results of the cost computation methods with the minimum spanning tree aggregation%

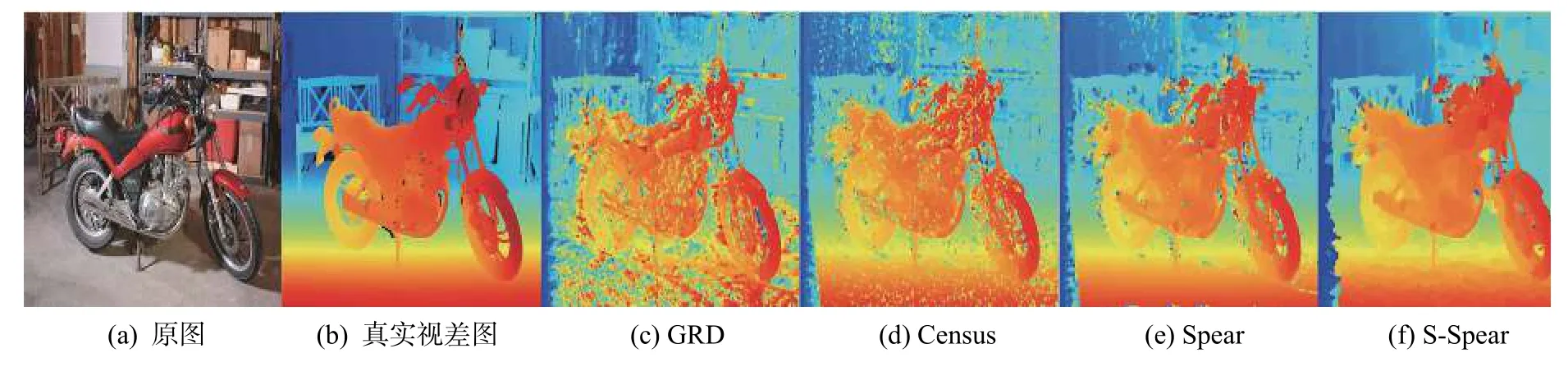
图2 不同匹配代价算法所得的Motorcycle 图像对的视差图Fig.2 Disparity maps of the Motorcycle image pair for all cost computaion methods（without disparity refinement processing）

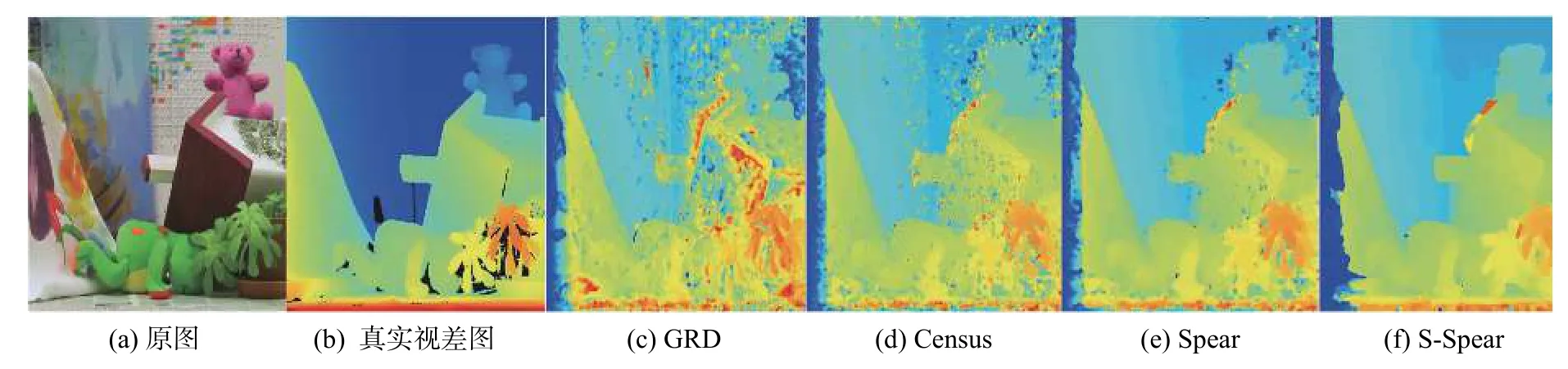
图3 不同匹配代价算法所得的Teddy 图像对的视差图Fig.3 Disparity maps of the Teddy image pair for all cost computaion methods（without disparity refinement processing）

3 结束语

提出了一种融合Spearman 算法的多尺度立体匹配算法。在代价计算阶段，通过Spearman 算法的演变得到两种代价计算模型。在代价聚合阶段，通过融合多尺度框架，使得匹配精度进一步提高，匹配的抗干扰能力进一步增强。实验结果表明，所提算法在Middlebury 测试平台上胜过其他代价计算方法。但是，从误差标记的视差图可以看出，所提算法在细节区域中精度还有待提高，今后的研究将针对细节作进一步的研究。