基于时域波形再现技术的车架焊缝疲劳寿命研究

2020-04-10高大威李智垠尚祎晨

上海理工大学学报 2020年1期

高大威，李智垠，尚祎晨

（上海理工大学机械工程学院，上海 200093）

车架焊缝疲劳损坏是影响汽车使用寿命的因素之一。在设计中考虑焊缝的疲劳寿命，才能避免车架关键区域在早期使用过程中出现疲劳损坏。传统的疲劳分析主要针对静强度问题，但在实际工况中，车架焊缝受路面不平引起的激励、发动机的工作振动等随时间变化的动态载荷，传统疲劳分析方法并不能准确预测其实际使用寿命。因此，提取动载荷准确预测车架焊缝疲劳寿命的研究具有重要理论意义和使用价值。

文献[1]以虚拟试验场法来进行时域波形复现，利用搭建的多体动力学模型进行虚拟迭代，求得反应路面不平度的路面激励信号。文献[2]介绍了较为先进的时域波形复现迭代自学习控制法，更加精确的频率响应函数（frequency response function，FRF）将会增加复现波形的准确性和鲁棒性。方剑光等[3]利用试车场采集的道路载荷谱和搭建的多体动力学模型，反求出路面激励，经过目标信号迭代后求出车轮轴头处的位移，进一步进行载荷分解得到车身载荷谱。Dannbauer 等[4]利用ADAMS软件搭建多体动力学模型，目标信号在软件中虚拟迭代，并将输出的动态载荷作为疲劳分析输入载荷，在有限元软件FEMFAT 中对车辆的前悬进行了疲劳寿命分析。文献[5-6]提出等效结构应力法，用于焊接接头的疲劳评定中，提高了焊缝疲劳寿命的预测精度。

为了能准确地预测出车架第三横梁和纵梁连接处焊缝的使用寿命，本文将经过处理的道路载荷谱进行目标信号虚拟后施加到搭建好的刚柔耦合多体动力学模型上，分解得到各连接点的时域动态载荷谱，作为车架焊缝有限元模型的输入谱，结合材料的疲劳特性曲线，计算出车架目标位置焊缝的疲劳寿命并给出优化方案，验证了该方案的有效性。

1 试验场数据采集

本研究的道路数据来源于国内某大型试车场。为了分别采集满载和空载两种载重状态下28 种道路工况的200 多个通道的力、力矩、加速度及位移等时域数据，在同一型号的试验车辆上分别安装相应的传感器。

在试验车辆的4 个轮心处安装轮心六分力仪，用来测量轴头3 个方向上的力（Fx，Fy，Fz）与力矩（Tx，Ty，Tz）；在车辆轴头、质心、前后减振器等位置安装加速度传感器，用来传递以上各处的加速度信号；在前后减振器支座处安装位移传感器，用来传递位移信号。以车轮六分力仪实测的垂向力Fz作为后续迭代过程中的目标信号，其他实测信号作为监控信号同样参与迭代。图1（a）为右后轮六分力测量仪，图1（b）为前减振器安装点三向加速度传感器。根据路况的不同将测量数据分类，并消除毛刺漂移。

图1 试验车辆上的传感器Fig.1 Test sensors on the test vehicle

2 多体动力学模型搭建

搭建精确的多体动力学模型是疲劳寿命研究的重要前提。通过整车多体动力学模型，可对采集的道路载荷谱进行分解，获得目标焊缝区域疲劳寿命分析所需的动态载荷谱。

2.1 前后悬架搭建

采集前后悬架的模型的硬点、刚度、阻尼、质量、构件质心坐标、转动惯量等参数，使用LMS Virtual Lab 软件中的Motion 模块搭建模型，以非线性曲线和Bushing 模型来拟合衬套、悬置、缓冲块等非线性部件相应的力学特性。

前悬架系统由前悬子系统、转向子系统、试验台子系统和前稳定杆Beam 梁子系统组成。上述多体动力学模型搭建过程的重难点在于转向系统的拓扑关系建立以及Beam 梁建模。根据已采集的参数建模，可以搭建出如图2（a）所示的前悬架多体模型。

同理，可搭建如图2（b）所示的后悬架多体模型。

图2 前后悬架模型搭建Fig.2 Multi-body model of suspensions

2.2 刚柔耦合整车模型搭建

对于刚柔耦合整车动力学系统，将车架视为柔性体子结构，结合固定界面模态综合法（craigbampton，简称CB 法），获得满足需要的解。单个柔性体视作子结构，其结构动力学方程为

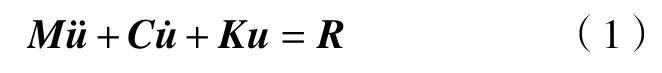
式中：M，K，C，R，u分别为子结构的质量矩阵、刚度矩阵、阻尼矩阵、外力矩阵及坐标矩阵；为加速度矩阵；为速度矩阵。

在CB 法中，前后悬架子结构视为刚体，其模态已经包含在约束模态中，在分析动力学问题时，不必将刚体模态分离出[7]。整车刚柔耦合模型的建立包含以下几部分：子机构的装配、试验台的添加、进一步调节部件的质心位置和转动惯量等参数、添加相应的约束。进行整车静平衡状态载荷对标之后，刚柔耦合整车模型如图3 所示。

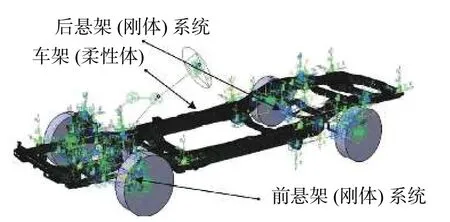
图3 刚柔耦合整车模型Fig.3 Rigid-flexible hybrid modeling

3 目标信号迭代

由于仿真过程的不稳定性，直接将目标信号（轴头垂向力Fz）加载于不受约束的多体模型时会发生模型的漂移和翻转现象。而在假设轮胎模型为理想模型的情况下，通过轴头的垂向位移时域信号可以间接地表示路面不平度激励，将该位移信号施加到多体动力学模型上时，模型不会发生翻转和漂移。故需将实车采集到的力信号转化成动力学模型的位移驱动信号。

3.1 时域波形复现法含义

搭建的整车多体动力学模型在不考虑轮胎非线性的条件下仍然具有高非线性[8]，为了避免模型非线性对复现试验目标信号带来的影响，需要迭代逆向求出多体模型的位移驱动信号。时域波形复现（time wareform replication，TWR）即该逆向迭代反算位移信号的过程，由两大部分组成：多体动力学模型系统识别和目标信号迭代运算。

3.2 多体动力学模型系统识别

系统识别是求解系统频率响应函数（FRF）及其反函数的过程，该频率响应函数表征了上述虚拟试验台架测试系统在给定频率下的稳态输出与输入的关系，其流程如图4 所示。

通常情况下，整车的频率f的范围在40 Hz 以下，选用目标频段范围设置在0.5～40 Hz 的白粉红噪声[9]WPN作为系统识别激励信号。白粉红噪声在频域范围内由式（2）确定。

式中：fst为起始频率；fb为边界频率；fend为终止频率；p为控制系数。

图4 系统识别流程Fig.4 Process of system identification

通过运算后可得到轴头激励的频域和时域信号。对时域内激励信号和响应信号进行快速傅里叶变换，可以了解激励信号和响应信号在频域内的情况。设时域内激励信号为u(t)，响应信号为y(t)，运用软件LMS Motion-TWR，经过傅里叶变换得出激励和响应的频域信号分别为U(f)和Y(f)。定义U*(f)和Y*(f)分别与U(f)和Y(f)是复共轭的关系，Iuu(f)和Iuy(f)分别是u(t),y(t)的自功率谱和互功率谱[9]，且存在如式（3）的关系。

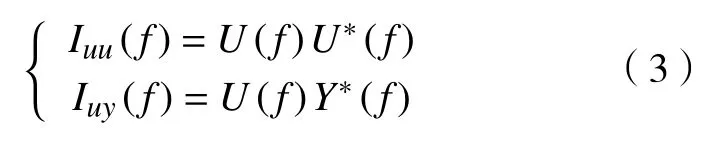
系统频率响应函数

与多体动力学模型具有高度非线性不同，通过系统识别得到的系统频率响应函数FRF 是线性的。因此，需要对FRF 精度进行评估。系统频率响应函数H(f)与自功率谱Iuu(f)，Iyy(f)和互功率谱Iuy(f)有如式（5）的关系。

通过软件LMS Motion-TWR，对于多输入多输出的系统（MIMO），可计算输入输出信号之间的多重相干函数，即各频率上分量间的线性相关程度，来评价FRF 质量[10]，如式（6）所示。

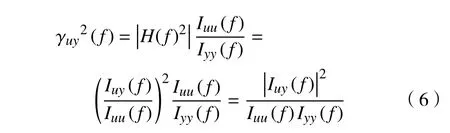
式中：0≤γuy2(f)≤1，当系统没有其他信号干扰时，γuy2(f)=1，代表输出完全由输入引起；若输入信号与输出信号不相干，γuy2(f)=0；若γuy2(f)≥0.8，可以认为频率响应函数估计的可信度较高，该值越接近1，说明系统识别的质量越高。

当相干函数小于0.8 时，说明该次系统识别激励信号不满足要求，应当对采用的白粉红激励信号进行调试，直至相干函数符合要求。图5 为4个轴头的相干函数C，可知系统识别得到的频率响应函数质量较高。

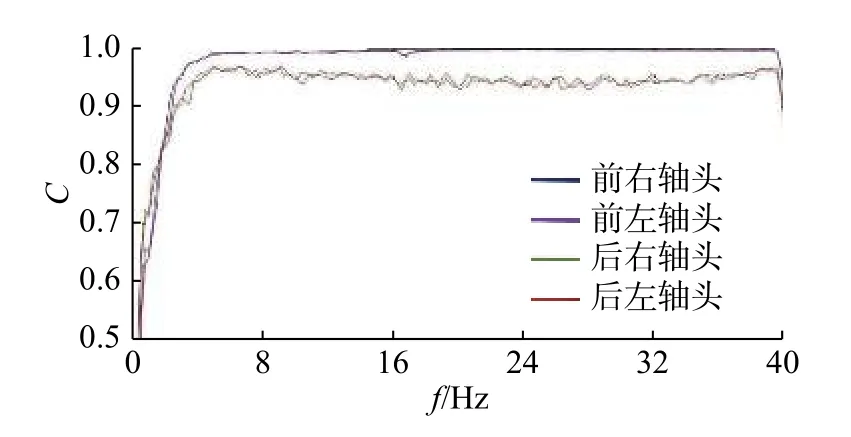
图54 个轴头的相干函数Fig.5 Coherence function of the four shaft heads

3.3 目标信号迭代

通过轮心轴头的垂向力信号和系统识别求出的频响函数FRF 的反函数H-1(f)反求初始的位移驱动信号u0(t)，如式（7）所示。

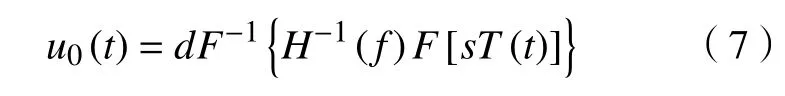
式中：s为目标信号系数；d为驱动信号系数；F为傅里叶变换；F-1为傅里叶逆变换；t为时间；T(t)为时域内垂向力信号。

信号迭代流程如图6 所示。

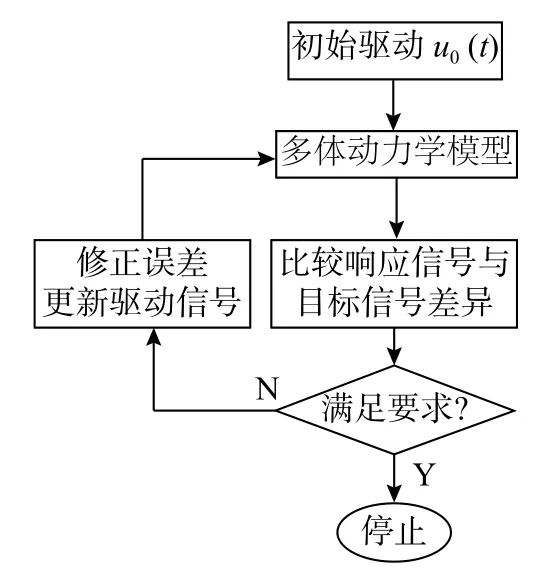
图6 信号迭代流程Fig.6 Process of signal iteration

由此可得第n次迭代时的驱动信号为

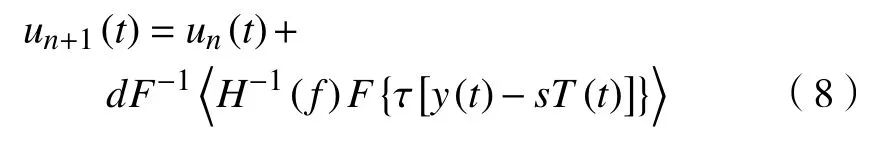
式中：n为迭代次数；τ为误差加权系数。

迭代的收敛速度取决于模型的精度，也取决于式（7）和式（8）中的各迭代调控参数。在计算机迭代中，应合理设置目标信号大小，并在每完成一次迭代后根据响应信号和目标信号的波形调整下一步迭代中的各系数。

迭代结果可通过3 种方式评估：时域频域波形重合度评估、伪损伤比评估、软件Responses/Targets Display 功能评论。在波形重合度评估中，除了观察目标信号和迭代信号的波形外，也需观察同一次迭代中监控信号的迭代情况。以中等比利时路况为例，图7 为时域下左后轴头垂向力迭代局部情况。将最后迭代得到的响应信号施加于多体动力学模型上，输出连接点的动态载荷谱，图8 为分解出的左前下控制臂前端点六分力载荷谱。

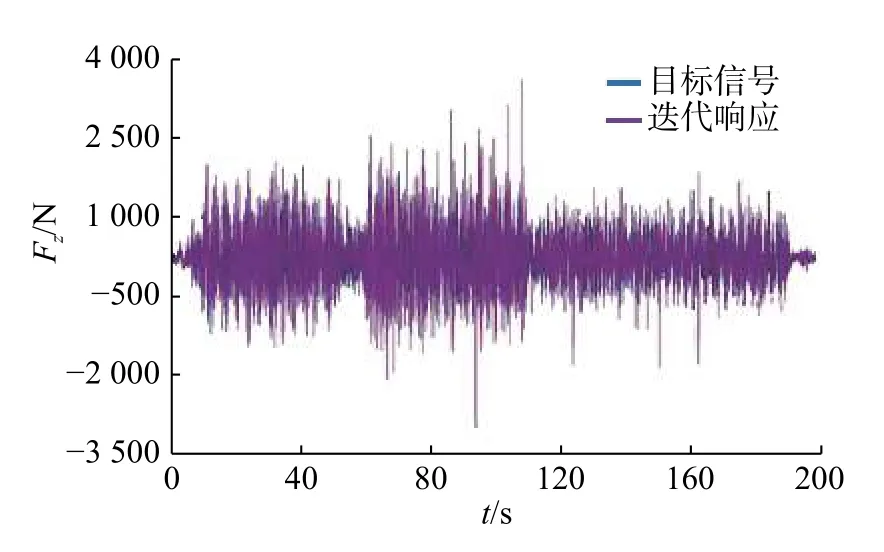
图7 时域下左后轴头垂向力迭代局部情况Fig.7 Spectrum of vertical force at the rear-left shaft head

4 车架焊缝疲劳寿命分析

分别对选定区域中的48 个关键位置进行静力分析，在Nastran 软件中对每个连接点的6 个方向上分别施加单位载荷以了解不同方向载荷对结构的影响[11]。经分析，垂向和侧向载荷在实际使用过程中对目标焊缝疲劳损伤贡献量较大，故应着重研究垂向载荷和侧向载荷较大的路况。依据准静态法，利用静态载荷组结合时域载荷谱去替代载荷作用点所受到的实际外部动态载荷，可获得构件动态应力分布。动态应力的数学表达式为[12]

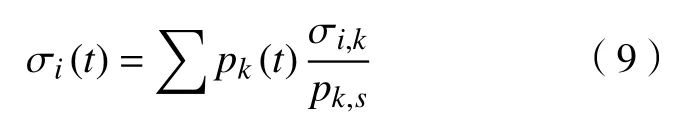
图8 左前端下控制臂前端点六分力Fig.8 General force at the front-left lower control arm

式中：σi(t)为某位置的应力时间历程；k为载荷序号；pk,s为第k种静态载荷；pk(t)为与pk,s相应位置处的载荷时间历程；σi,k为静态载荷k产生的应力响应。

4.1 Volvo 法焊缝寿命求解

Volvo 法是nCode 软件Seam Weld 模块下降低有限元模型焊缝单元网格尺寸敏感性，对焊缝疲劳寿命进行求解的一种方法。

焊缝单元应力一般由弯曲应力σb和拉压应力σn线性叠加而成。指定节点的弯曲程度通过挠度比率r表示。

显然，0≤r≤1。若r=1，则表示单元呈现的是纯弯曲的柔性状态；若r=0，则表示单元呈现的是纯拉压的刚性状态。常取阈值rth=0.5 为判断标准[7]。当0≤r≤rth时，则选用r=0 的刚性S-N曲线；当rth≤r≤1 时，选用插值法结合刚性和柔性S-N曲线。N为材料或构件的疲劳寿命，S为应力。因计算得到的裂纹焊趾处单元挠度比率均远小于0.5，故选择刚性S-N曲线作为材料属性。

在各种迭代路面中，中等比利时路况使车架承受较大的垂向载荷，蛇形规范路况使车架承受较大侧向载荷。将这两种路况分解成48 个关键点的动态载荷谱并与有限元模型结合，最终利用Seam Weld 模块求解出中等比利时路况单次里程焊缝寿命为6 010 次，蛇形规范路况单次里程焊缝寿命为9 950 次。