具有两种不同阻尼模型的非黏滞阻尼系统的状态空间方法

修国众，时 宝，王丽英

（海军航空大学航空基础学院，山东烟台264001）

0 引 言

黏性阻尼模型是最常用的振动阻尼模型，因具有简单性和便利性的特点，黏滞阻尼模型被广泛应用，即使真正的阻尼特性被认为是非黏性的.耗散力依赖于瞬时广义速度以外的任何量的阻尼模型称为非黏滞阻尼模型，相应的振子称为非黏滞阻尼振子.在许多非黏滞阻尼模型中，卷积型非黏滞阻尼模型可能是线性分析范围内最一般的模型［1］.

考虑卷积型非黏滞阻尼模型是阻尼与质点速度的历史相关，假设阻尼可以表示为核函数与质点的速度的卷积，即

其中，G(t)是核函数；ẋ(t)是质点的相对速度.

在文献［2-4］中，作者提出许多卷积型非黏滞阻尼模型来精确描述黏弹性材料的耗散机理.阻尼模型有几种物理上真实的数学形式，如Biot模型［5］在拉普拉斯域可表示为：

一些作者将流变学理论应用于线性黏弹性模型，如广义麦克斯韦模型［6］：

在许多阻尼模型中，指数阻尼模型［7］在物理上最有意义，也是应用最为普遍的，在拉普拉斯域表示为：

在动力设计中经常会遇到具有两个或两个以上不同耗能水平的机械工程系统，因此这些阻尼系统往往涉及多个不同的阻尼模型.然而，在文献［8-9］中，作者只讨论单一的指数阻尼系统；ADHIKARI［10］提出了指数型阻尼线性系统的精确状态空间方法；WAGNER 等［11］提出了一种基于运动方程扩展状态空间的表示方法，该方法除了利用位移和速度作为状态向量外，还利用了一组内部变量，本文作者在本研究中也使用了该方法；LI 等［12］提出了用有理多项式的分式（广义阻尼模型）来描述多个阻尼模型的想法，试图用统一的阻尼形式来表示不同的阻尼模型，为本文作者求解具有两种不同阻尼模型的非黏滞阻尼系统提供了思路和方法.

本研究的目的是创建具有两种不同的阻尼模型的非黏滞阻尼系统的状态空间公式.在第一节中，将给出具有两种不同阻尼模型的三自由度非黏滞阻尼系统的拉普拉斯域运动方程，根据最小实现理论，将两种不同阻尼模型构造为矩阵相乘的形式，通过使用Kronecker 积将系统方程写成简化形式；在第二节中，通过引入内部变量变换，得到了时间域上的一阶线性系统.作为一个特殊例子，考虑了指数阻尼系统，得到了类似于文献［11］的指数阻尼系统的状态空间方法，验证了该方法的有效性.

1 具有两种不同阻尼模型的非黏滞阻尼系统的一般形式

图1为三自由度非黏滞阻尼系统的力学模型图.该系统有3个质量块，每个质量块为m，并由刚度系数为k 的弹簧连接.系统的非稳态阻尼模型由两种不同的阻尼模型组成，如图1 阴影部分所示.其中，G1(t)是Biot阻尼模型，G2(t)是指数阻尼模型.

图1 具有两种不同阻尼模型的三自由度系统

具有两种阻尼模型的三自由度非黏滞阻尼系统的拉普拉斯域运动方程可以表示为：

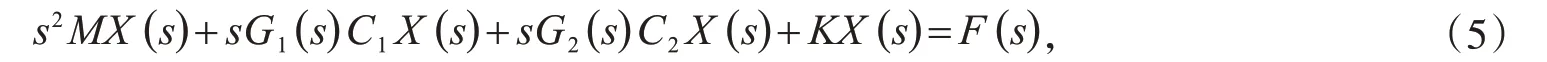
其中，M(M ∈R3×3)和K(K ∈R3×3)分别是系统的质量矩阵和刚度矩阵；C1'C2(C1'C2∈R3×3)是频变阻尼系数矩阵；G1(s)，G2(s)是频变阻尼函数；F(s)是外力向量；X(s)表示响应向量.假设：

不大于分母的阶数qk，即pk≤qk，并且qk≥1，则根据最小实现理论，有理多项式可以表示为：

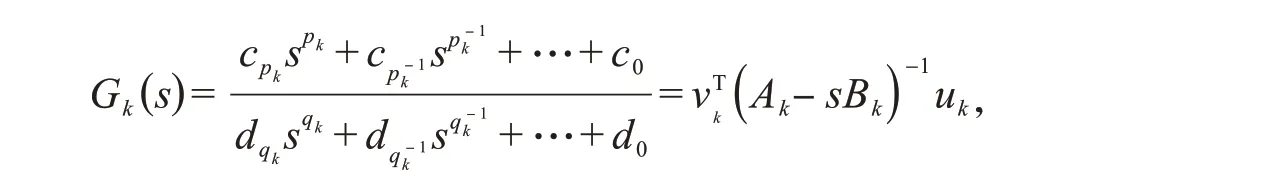
其中，矩阵Ak'Bk∈Rqk×qk；向量vk'uk∈Rqk×1.一般假设分母最高次阶项的系数为1，即dqk=1，则可将上述矩阵和向量构建为：

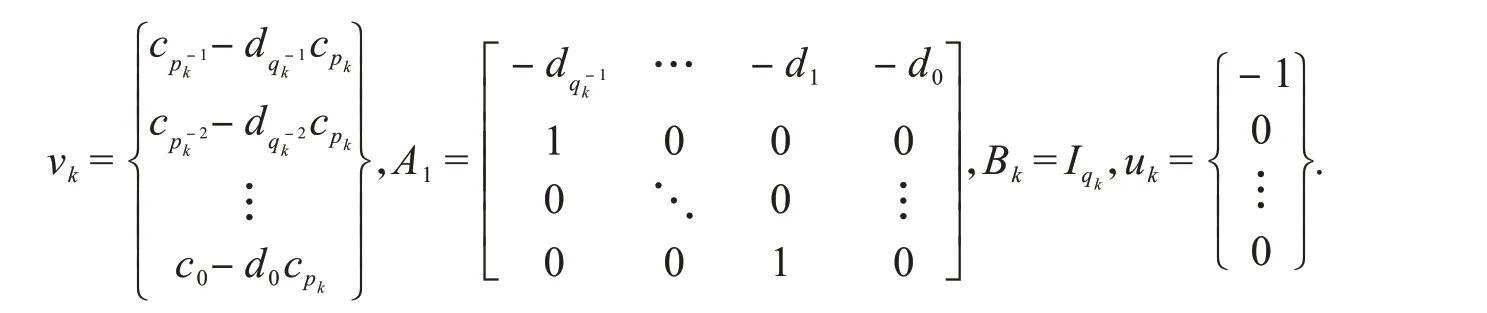
假设系统的两种阻尼模型：一种是两个系列的Biot阻尼模型；一种是两个系列的指数阻尼模型.将这两种不同的阻尼模型根据引理可表示为有理多项式的形式：

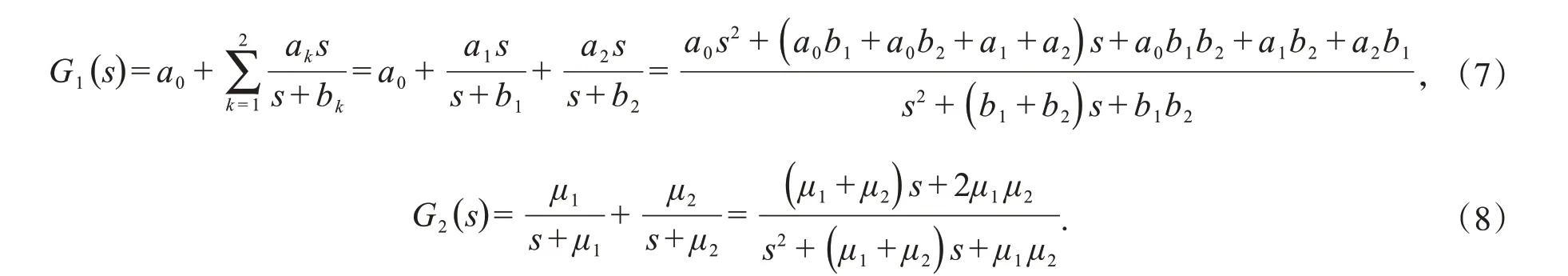
因为分子和分母没有公因子，则可以根据引理写成形式：

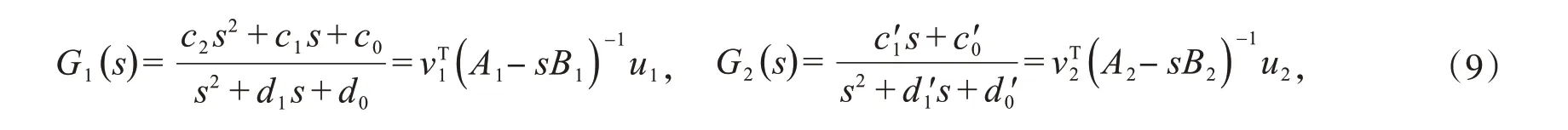
其中，矩阵A1'B1∈R2×2，A2'B2∈R2×2；向量v1'u1∈R2×1，v2'u2∈R2×1.矩阵和向量可表示为：

通常，阻尼材料只是整个系统的小部分，这意味着频变阻尼系数矩阵C1，C2∈ℝ3×3不是一个全秩矩阵.假设矩阵Ck的秩是rk，则有：

因此，系数矩阵Ck可分解为：

由上述假设，则有：

其中，Irk表示秩为rk的单位矩阵.

定义Kronecker 积是两个矩阵间的运算.Kronecker 积是张量积的特殊形式，以德国数学家利奥波德克罗内克命名，用符号⊗表示.假定A 是一个m×n 的矩阵，B 是一个p×q 的矩阵，Kronecker 积A⊗B则是一个mp×nq的分块矩阵：

由Kronecker积定义，可以将式（13）替换为：

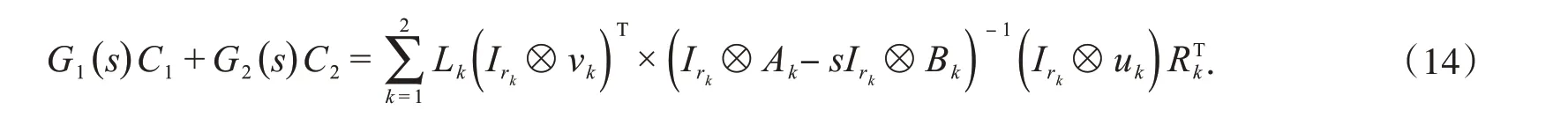
令：

可得：

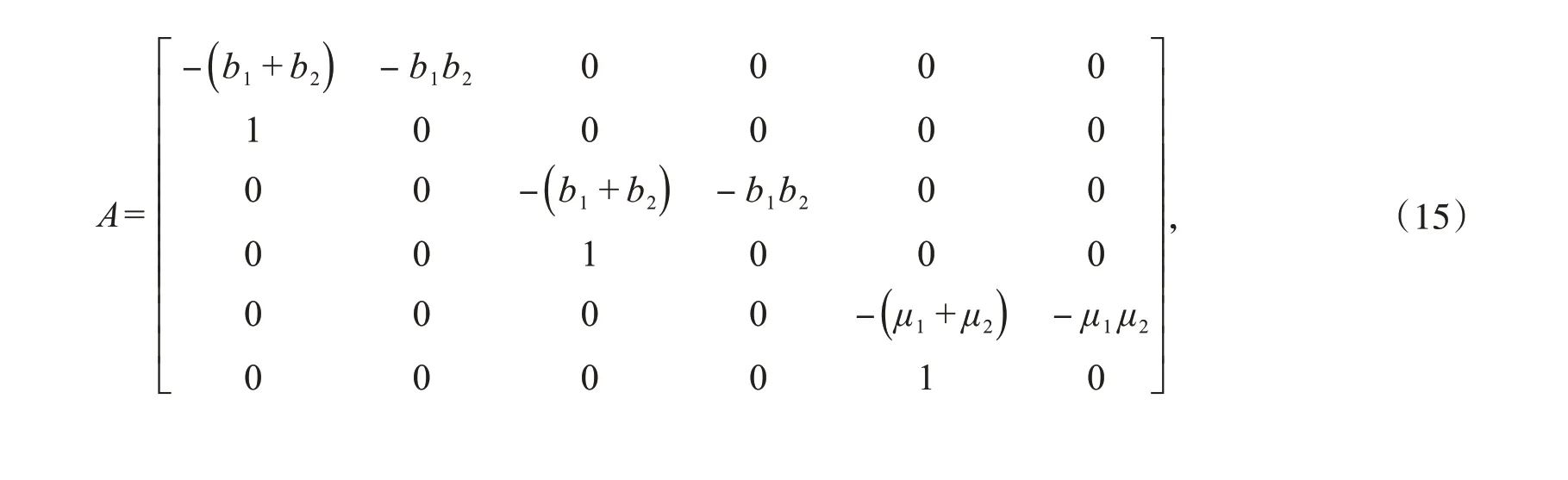
则式（13）可以简化为：

将式（19）代入式（5），则式（5）可以简化为：

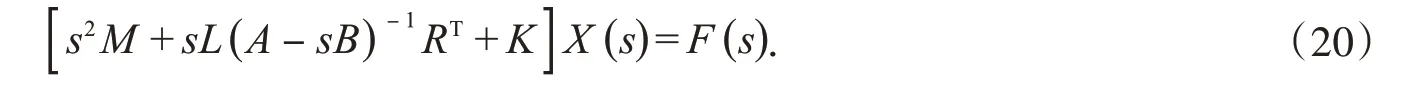
2 具有两种不同阻尼模型的三自由度非黏滞阻尼系统的状态空间方法

为了建立该系统的状态空间公式，引入内部变量：

式（21）两边同乘以(A-sB)-1，可得：

为了获得内变量的时变行为，通过拉普拉斯逆变换得以下形式：

其中，x(t)=ℓ-1[X(s)]，y(t)=ℓ-1[Y(s)].将式（21）代入式（20），再利用拉普拉斯逆变换，得到一个增广耦合系统：

假设质量矩阵M是非奇异的，引入黏滞阻尼系统的常用状态向量：

由式（23）～（25）可以构建线性系统：

假设矩阵A是非奇异的，则式（23）可化为：

将式（27）代入式（24），则得：

由式（25），（27）和（28）可构建线性系统：

定理具有两种不同阻尼模型的三自由度非黏滞阻尼系统的拉普拉斯域运动方程为

系统的两种阻尼模型，一种是Biot 阻尼模型如式（7），另一种是指数阻尼模型如式（8），则可得到该系统时间域上的状态空间公式如式（29），并且

由这些系统矩阵，用模态叠加法可得到系统的动态响应.

为了验证该方法的有效性，假设系统只有指数阻尼模型，Biot阻尼模型为0，则指数阻尼系统的拉普拉斯域运动方程可以表示为：

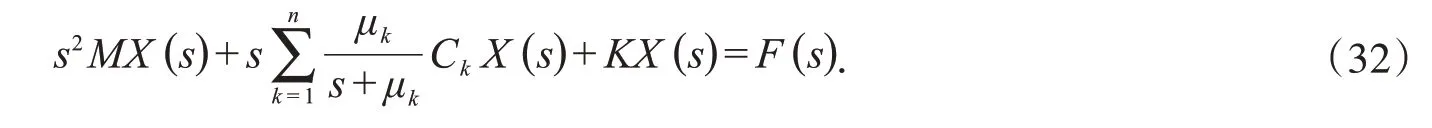
根据引理，指数阻尼模型可表示为：

由定理可得系统矩阵：

这一结论类似于文献［11］指数阻尼系统的状态空间方法.如果式（32）的系统矩阵是对称的，可得Lk=Rk，则系统（33）也是对称线性的.

3 结 论

在动力设计中，经常遇到两个或两个以上耗能水平显著不同的机械工程系统，这些系统往往涉及多种阻尼模型.本文作者对具有两种不同阻尼模型的三自由度非黏滞阻尼系统进行分析，运用Kronecker积将拉普拉斯域的系统方程化简为一般系统的形式，再引入内部变量变换创建了一种基于常状态向量的非黏滞阻尼系统状态空间公式.并以指数阻尼系统为例，验证了状态空间公式的有效性.状态空间公式可以简化为常见的黏滞阻尼系统和指数阻尼系统的形式，这种拓展的状态空间公式可应用于具有多种阻尼模型的非黏滞阻尼系统的分析.