转运通道中燃料组件沸腾传热的试验研究
2020-04-09毛喜道
毛喜道,夏 虹
(1.哈尔滨工程大学 核科学与技术学院,黑龙江 哈尔滨 150001;2.中国核电工程有限公司,北京 100840)
压水堆核电站采用的燃料组件通常为棒束结构。在反应堆换料过程中,水平放置的乏燃料组件要通过1条水下通道完成从反应堆厂房到乏燃料水池的运输。这条水下通道称为转运通道,采用水平布置,贯穿安全壳。在转运通道中,乏燃料组件由带孔的承载器和运输小车承载和保护[1-2]。在运送过程中,存在多种可能的原因,如机械故障、失电等,使乏燃料组件较长时间滞留于仅存在自然循环冷却的转运通道中。为确保水平放置的燃料组件在通过转运通道时的热工安全,防止燃料包壳过热[3],需研究乏燃料组件在转运通道中的传热问题。课题前期已针对正常卸料工况和事故卸料工况开展了试验研究,获得了单相自然对流条件下转运通道中燃料组件顶角传热条件恶劣区域的局部传热特性[4]。本文考虑更加极端的热流密度参数和水温参数,以研究沸腾条件下燃料组件的传热特性。
1 乏燃料组件在转运通道中的换热
转运通道中燃料组件棒束呈水平状态,其沸腾过程与水平管束池沸腾有一定的相似性。工业领域中,管束池沸腾传热问题主要集中于化工及动力换热设备,如再沸器、蒸发器等。在目前的工程设计中,管束池沸腾传热计算以单管换热系数叠加修正项的经验关联式为主。
在池沸腾研究方面,针对壁面材料、表面特性、工质物性等影响沸腾的不同因素,各国学者开展了许多研究。其中Rohsenow池沸腾关联式获得了较广泛的应用[5],计算平板、单管等工况时具有一定的准确性。但由于影响沸腾的因素比较复杂,在部分工况下Rohsenow关联式的计算误差会在±50 %以上[6-7]。因此,为提高计算准确性,针对不同的条件和工况,往往需开展不同的专门试验来得到针对性强的计算式。
水平管束池沸腾过程较单管情况更为复杂,管束中下部加热管产生的气泡对上部管的冲刷会减薄液膜,同时引起气泡的聚合和提前脱离,强化上部管的传热。Kang[8-9]针对双管管束开展了管束效应机理研究,朱长新等[10]、贾岫庄等[11]、施明恒等[12]、龙恩深[13]和田文喜等[14]针对多管管束开展的核态池沸腾研究结果均证实了上述现象。也有研究发现,在较高热负荷情况下,管束下部产生的气泡会形成包覆效应,使上部管的传热系数增长减弱[15],甚至减弱上部管的传热[10]。由于水平管束池沸腾过程的复杂性,大部分研究者都认为水平管束池沸腾传热没有普遍适用的关系式[16]。
在转运通道承载器中水平放置的燃料组件池沸腾过程,与再沸器、蒸发器等水平管束有一定的区别,因为组件的冷却水入口和顶部蒸汽出口均受到承载器开孔的阻碍,如图1所示,燃料组件顶部的部分燃料元件处于一种半封闭状态,蒸汽易在此位置发生聚集而影响换热,目前尚无文献报道该几何条件下的水平管束池沸腾特性。本文对易发生蒸汽聚集的水平燃料组件顶角区域开展沸腾试验,根据试验结果和数据,拟合传热的关联式。

图1 燃料转运通道、承载器和燃料组件示意图Fig.1 Schematic of fuel transfer tube, carrier and fuel assembly
2 试验装置和参数范围

图2 试验段三维模型Fig.2 3D model of test facility
本试验装置的设计和布置见文献[2,4]。试验段的内径与转运通道原型相同,轨道、承载器的横截面方向的几何尺寸也与转运装置原型相同,试验中用电加热组件模拟燃料组件的中间部分。图2为试验段的三维示意图,图中:1为位于转运通道中心对称面的燃料组件,试验中由750 mm长的电加热组件模拟;2为模拟承载器;3为模拟转运小车;4为冷凝器,将试验段产生的饱和蒸汽冷凝为饱和水,用于模拟转运通道两侧水池进口处蒸汽和水的交换。在1和4中间增加了网状阻力元件,用于补偿本试验段之外转运通道中流体的压力损失。为保持试验段中压力稳定,试验段外设置了容积补偿器。在试验段底部设置了用于补偿散热的辅助加热器。
整个沸腾试验过程中,试验段压力维持在0.1 MPa,燃料组件两侧入口的过冷度精确控制在0.5 ℃以内。模拟燃料加热组件表面热流密度的范围为2 400~20 000 W/m2,加热棒材质为经过抛光的316L不锈钢,表面粗糙度Ra≈0.8 μm。根据前期研究成果[1,4],燃料组件顶角部分受到承载器壁面的影响,传热条件较差。同时,由于承载器上壁面不利于气泡排出,蒸汽易在此位置发生聚集,如图3所示。

图3 承载器顶角处加热棒壁温测量示意图Fig.3 Schematic of wall temperature measurement in upper corner of fuel carrier
由于受到试验本体的空间限制,试验中仅分别测量了1#、3#和5#加热棒的顶部壁温,如图3所示。为保证试验精度,温度测量采用一级精度T型热电偶,压力测量采用罗斯蒙特3051压力变送器。仪表在使用前均进行了校准。由于沸腾换热系数计算中需要壁面温度和入口水温的差值,为减小测量误差,试验中壁温和水温采用了相同模/数转换通道和冷端补偿温度,其差值可消去模/数转换和冷端补偿等误差。综合考虑校准不确定度和补偿导线引入的不确定度,试验测量范围内,温差测量95%置信水平下不确定度为±0.6 ℃;压力测量误差为±0.14%。
为排除加热管壁面不稳定的汽化核心对试验结果的影响,在正式试验前,开展了加热管表面老化工作。试验从低热流密度向高热流密度进行,在每个工况稳定0.5 h后,再记录加热棒的功率和各热电偶温度,同时观察管束沸腾现象。
3 试验结果分析
3.1 沸腾换热曲线
图4为沸腾换热系数与热流密度的关系。图4中黑色实线为采用Rohsenow[17]关联式计算的单棒池沸腾换热系数曲线,用于与燃料组件试验结果进行对比。从图中可看出,燃料组件1#、3#和5#加热棒顶部沸腾传热系数均高于单棒的情况。燃料组件试验段各顶部测量棒的换热系数随热流密度的增加而增大,但随热流密度的增大,换热系数增大的幅度变缓。
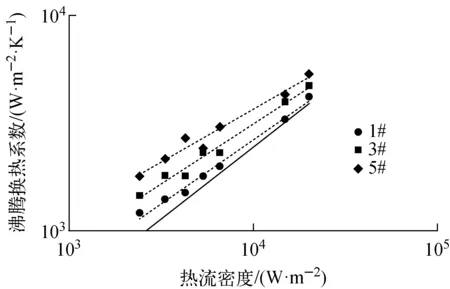
图4 沸腾换热系数与热流密度的关系Fig.4 Relationship of boiling heat transfer coefficient and heat flux
1#棒位于承载器的顶角部位,水和气泡的运动受到承载器的影响最大,这在图4中也有所体现:1#棒的沸腾换热系数是3根棒中最低的。随着加热棒远离承载器的顶角,沸腾换热系数逐步增大。
图5为1#、3#和5#加热棒顶部沸腾传热系数实验值与Rohsenow关联式计算值之比htop/h1(htop为顶角处加热棒顶部局部沸腾换热系数,W·m-2·K-1;h1为Rohsenow关联式计算值)与热流密度的关系。从图5可看出,随加热棒壁面热流密度的增大,1#、3#和5#棒与单管的沸腾换热系数的比值逐步减小。其中,在壁面热流密度约为20 000 W/m2时,1#棒的换热系数已接近单棒值,说明此时承载器顶角处气泡聚集的包覆效应已基本抵消了管束效应。

图5 htop/h1与热流密度的关系Fig.5 Relationship of htop/h1 and heat flux
3.2 换热关联式
从图4可知,燃料组件顶角处,加热棒顶部沸腾换热系数随位置和热流密度的变化而变化。试验过程中,系统压力为0.1 MPa,定性温度为试验系统压力下对应的饱和温度,池式沸腾特征长度l*=σ/[g(ρl-ρg)]。将沸腾换热系数参照Pior关联式[6]形式进行最小二乘拟合,如式(1)所示,则可获得1#、3#和5#棒位置处的局部沸腾传热系数经验关联式。
(1)
式中:q为加热棒表面热流密度,W·m-2;k为液体导热系数,W·m-1·K-1;hfg为汽化潜热,J·kg-1;ρg为气相密度,ρl为液相密度,kg·m-3;σ为表面张力,N·m-1;g为重力加速度,m·s-2;Pr为普朗特数;l*为池沸腾特征长度;C、n和m为待定系数。
根据试验数据分别求出htop、q、Pr和各物性参数后,通过多元回归分析,求出待定系数。式(2)~(4)分别为1#、3#和5#棒顶部沸腾换热系数拟合关联式,该组关联式适用于系统压力0.1 MPa、燃料组件进口冷却水水温接近饱和温度、热流密度在2 400~20 000 W/m2条件下的承载器顶角部位加热棒顶部饱和沸腾传热系数的计算。加热棒材质为经过抛光的316L不锈钢,表面粗糙度Ra≈0.8 μm。
h1,top=
(2)
h3,top=
(3)
h5,top=
(4)
图6示出了试验数据与拟合关联式计算结果的偏差。从图6可看出,除个别数据点外,3个拟合关联式与试验数据的偏差均在±10%以内,说明拟合关联式具有较好的准确性。

图6 试验结果与拟合关联式计算结果的偏差Fig.6 Deviation between experimental data and correlation results
4 结论
本文针对反应堆换料燃料转运通道中乏燃料组件池沸腾工况,研究了承载器顶角区域燃料棒的传热特性,结论如下。
1) 在试验参数范围内,承载器顶角区域中燃料组件最上排加热棒顶部的沸腾传热系数均高于Rohsenow关联式单管池沸腾传热系数计算值,但越靠近顶角的加热管的沸腾换热系数越接近单棒的沸腾传热系数。
2) 随热流密度的增大,燃料组件最上排顶角区域加热管饱和沸腾传热系数逐步增大,但与单管池沸腾传热系数的差异逐步减小。
3) 通过拟合实验数据,得到了承载器中顶角区域1#、3#和5#棒顶部的饱和沸腾换热关联式,可为后续工程应用中评估燃料组件在转运过程中的热工安全状态和表面最高温度提供参考。
