内阻尼对柔性连接转子系统稳定性的影响

2020-04-09白宇杰高剑波

原子能科学技术 2020年4期

白宇杰，高剑波

(核工业理化工程研究院，天津 300180)

工作在柔性支承下的高速转子系统容易发生动力学失稳，如美国航天飞机的液氢涡轮泵转子由于密封流体激振力引发次同步进动[1]，我国液氢涡轮泵转子由于内阻尼也发生了严重的失稳问题[2]。引发转子系统失稳的因素很多，常见的如油膜失稳、密封失稳、碰摩失稳和材料内阻尼失稳等[3]，确定失稳原因是进行转子支承系统设计的关键。目前柔性连接转子系统在试验中遇到进动失稳而无法正常升速，初步研究表明柔性连接处材料阻尼和结构阻尼构成的内阻尼是失稳的主要因素，需开展进一步研究以指导工程设计。

关于内阻尼对转子系统稳定性影响的研究较多[4-9]。白长青等[4]用黏性阻尼和滞后阻尼模型建立了考虑内阻尼的Timoshenko梁-转轴有限元模型，并分析了内阻尼对失稳转速的影响。Mendonca等[10]采用Ni等[11]的内阻尼模型分析了安装在复合材料转轴上的转子系统稳定性。Arab等[12]采用一维黏弹性理论建立了考虑内阻尼的铺层复合材料转轴的转子动力学稳定性。Vervisch等[13]用试验方式研究了旋转阻尼对失稳转速的影响。上述研究中的内阻尼模型主要面向柔性转子，关心的是转子的柔性模态，难以直接应用于本研究中的柔性连接刚性转子系统中。根据一维Kelvin-Voigt黏弹性理论的复数形式，可将连接处的材料阻尼和结构阻尼集总在柔性连接处的刚度中，形成考虑内阻尼的复刚度模型[14-16]。采用复刚度模型不仅可有效分析系统稳定性，且可从模态试验中获取代表内阻尼的虚部系数[17]。

本文根据Kelvin-Voigt黏弹性理论建立适用于柔性连接转子的复刚度模型，提出通过模态试验得到代表内阻尼的虚部系数的测试方法，在此基础上建立考虑内阻尼的转子支承系统动力学模型，分析内阻尼和减振器参数对稳定性的影响。

1 数学模型

1.1 内阻尼模型

对于在交变载荷下会产生内耗的材料，可采用Kelvin-Voigt黏弹性理论的一维本构关系进行描述，其应力应变关系如下：

(1)

其中：σ为应力；E为材料的杨氏模量；μ为材料的阻尼系数；ε为应变；t为时间。直接测量材料的Kelvin-Voigt黏弹性理论中的阻尼系数比较困难，相关文献非常少，本文通过以下方式间接获取。

假设在简谐激励下的应变为ε=ε0cosωt，则可得到应力应变的方程为：

(2)

其中：ε0为应变幅值；ω为激励频率。显然式(2)为椭圆方程，其中椭圆面积为材料循环1周所吸收的能量ΔU：

(3)

在循环1周中的最大弹性应变能U为：

(4)

于是可得到材料的损耗因子η：

(5)

在小阻尼情况下，对于转子本身的第i阶模态频率，可得到：

ηi≈2ξi

(6)

其中，ξi为第i阶模态的阻尼比，结合式(5)有：

(7)

测量无外阻尼时柔性连接转子本身的模态频率和模态阻尼比，根据式(7)就可得到某一模态频率激励下材料的阻尼系数，即得到该频率下材料的Kelvin-Voigt黏弹性理论的一维本构关系。但直接运用该本构关系推导转子系统的动力学方程较复杂，且会引入非线性项，对于建模和计算都会带来较大困难，因此本文考虑Kelvin-Voigt黏弹性理论的复模量形式。

假设ε=ε0eiωt，代入式(1)可得：

(8)

结合式(7)可得到适用于某一模态频率激励下材料的复模量：

(9)

上述推导得到的复模量模型主要适用于某一阶模态频率，同时柔性连接转子本身的内阻尼较小。如果转子系统在升速中主要发生某一阶模态失稳，则可采用该复模量模型。

1.2 动力学模型

图1为柔性连接转子支承系统，其中转子的左右两部分通过柔性连接件串联而成，转子的左端为弹性支承，右端为减振器，吸收振动能量并提供整个系统的阻尼。柔性连接件和转子直接通过结构配合完成连接，容易产生结构阻尼，同时本身材料阻尼较大，因此在整个转子中会引入较大的内阻尼。

对于图1所示的柔性连接转子支承系统，假设转子为轴对称刚体，仅在水平和竖直方向振动，支承特性各向同性，转子中部柔性连接件主要提供左右两部分转子的弯曲刚度，忽略剪切刚度，因此柔性连接处的振动位移一致。转子左右两端的长度、质量、极转动惯量、赤道转动惯量分别为L1和L2、m1和m2、Jp1和Jp2、Jd1和Jd2，转子中部柔性连接处的弯曲刚度为C，弹性支承刚度为k1，减振器主刚度为k2、集中质量为m3、次刚度为k3、阻尼系数为c3。整个系统包括转子左端(x1，y1)、中部柔性连接处(x2，y2)、转子右端(x3，y3)和减振器(x4，y4)共8个自由度。

图1 柔性连接转子支承系统Fig.1 Flexibly connected rotor support system

令转子以角速度ω旋转，计算转子支承系统的动能和势能，应用拉格朗日方程，可得到系统的运动方程为：

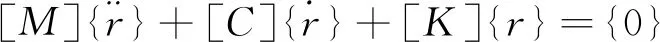
(10)

其中：{r}为虚数形式的自由度，即ri=xi+yi。系统中的质量矩阵[M]、阻尼与陀螺矩阵[C]和刚度矩阵[K]分别为：

(11)

(12)

(13)

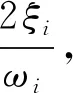
C*=C(1+idiω)

(14)

针对感兴趣的模态，在测量其模态频率和模态阻尼比后，根据式(9)就可得到相应的内阻尼系数，并将复弯曲刚度代入式(10)，即是考虑复模量的转子支承系统动力学方程。值得注意的是，根据静态下模态测试结果计算的内阻尼系数，在升速过程中可能会改变，尤其是柔性连接处相对运动导致的结构阻尼，更可能随转速而变化，不过在本文中暂不考虑该因素对内阻尼系数的影响，如计算结果精度不够可在下一步研究中进行修正。

本文研究的转子系统动力学方程，包含了保守力和循环力，可采用线性系统的Routh-Hurwitz准则判断系统的稳定性。但在考虑式(14)的复刚度后，矩阵中元素出现了复数，采用该准则还需进一步论证。幸运的是采用复刚度不改变系统的线性特征，因此可直接求解转子系统动力学方程的特征根，根据特征根的实部正负来判断系统从稳定到失稳的过程，即可得到系统的稳定性。

2 试验测试

2.1 模态测试

为了在转子支承系统动力学方程中应用复刚度，需获取式(14)中的虚部系数，因此需获得转子本身的模态频率和模态阻尼比。

由于转子本身含有柔性连接件，因此采用立式方法进行模态测试，转子上端用非接触式电磁轴承约束，下端放置于无阻尼的底座。激振方式为锤击法，拾振方式为贴在转子壁面上的加速度传感器。在转子壁面画好网格后，采用多点激振、单点拾振的方式进行模态测试，每个激振点重复测量3次。运用LMS Lab的模态分析模块进行数据处理，得到转子本身的模态频率和阻尼比，如表1所列。

表1 转子的模态频率、模态阻尼比和虚部系数Table 1 Modal frequency, damping ratio and imaginary part coefficient of rotor

由表1可知，本研究共测试了4个转子，统计了两个感兴趣的模态，分别是转子一弯和转子二弯，如图2所示。其中：转子一弯模态指的是转子左右两部分作为刚体围绕柔性连接体做刚性振动，该模态频率受柔性连接处弯曲刚度影响较大；转子二弯模态指的是转子左右两部分分别进行柔性振动，与转子材料性能关系较大，因此比转子一弯频率高得多。表1也列出相应模态的虚部系数，转子一弯的虚部系数在10-5量级，转子二弯的虚部系数在10-7量级。在进行数值分析时，会根据出现进动的频率选取相应量级的虚部系数进行计算。

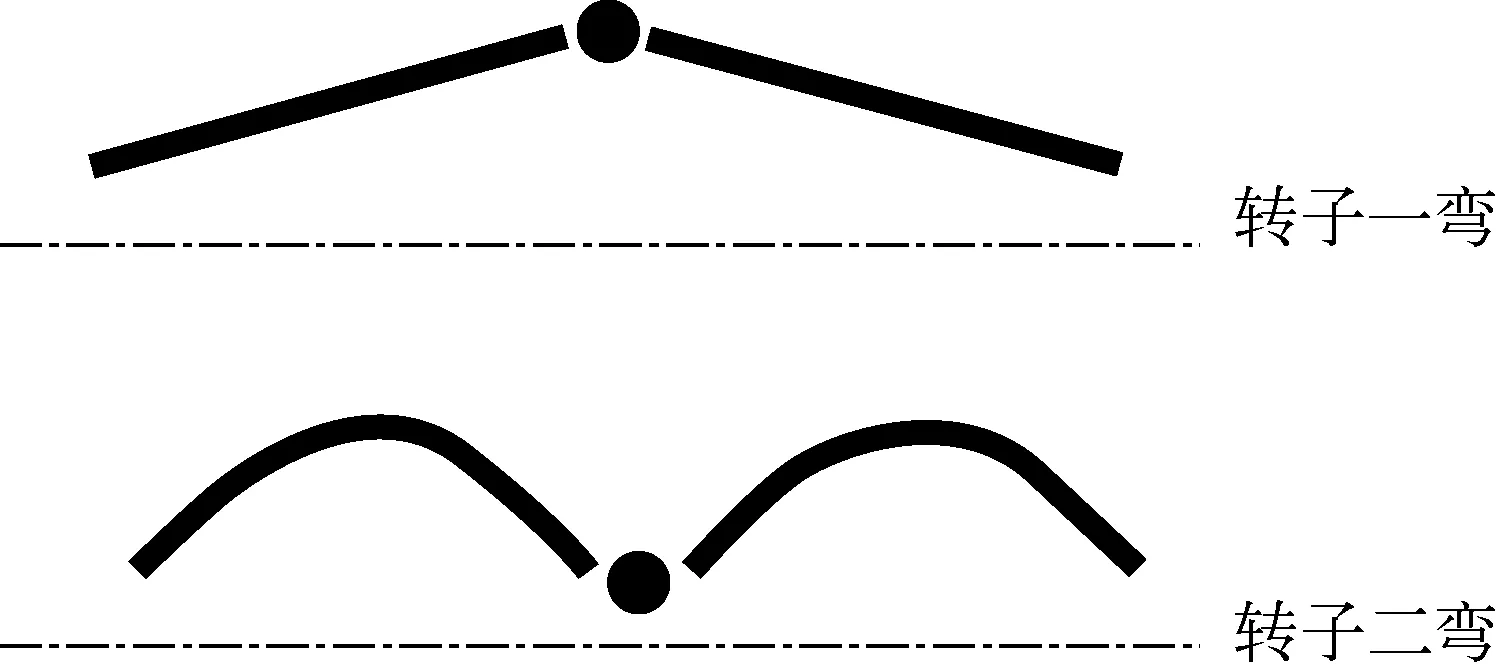
图2 转子一弯和转子二弯模态Fig.2 1st and 2nd bend mode shapes of rotor

2.2 升速试验

本文采用如图3所示的测试平台进行升速中的稳定性检测。测试平台包括左端提供弹性刚度的弹性支承和右端的减振器，其中减振器中较窄部分代表主刚度，较宽部分代表集中质量、次刚度和阻尼系数。转子水平地放置在弹性支承和减振器上进行旋转。通过两个正交的电涡流传感器采集转子柔性连接处的振动信号，采用LMS Lab软件对振动信号进行时域和频域分析。在开始采集后，进行转子升速，实时分析振动信号频谱中的主频是否为1×频率，是否会出现其余振动频率。在出现其他振动频率且不会衰减时，记录此时的转子转速，就得到进动出现的转速和相应的进动频率。在正式试验之前，转子均经过了良好的动平衡，不会出现振幅过大导致碰摩的问题。

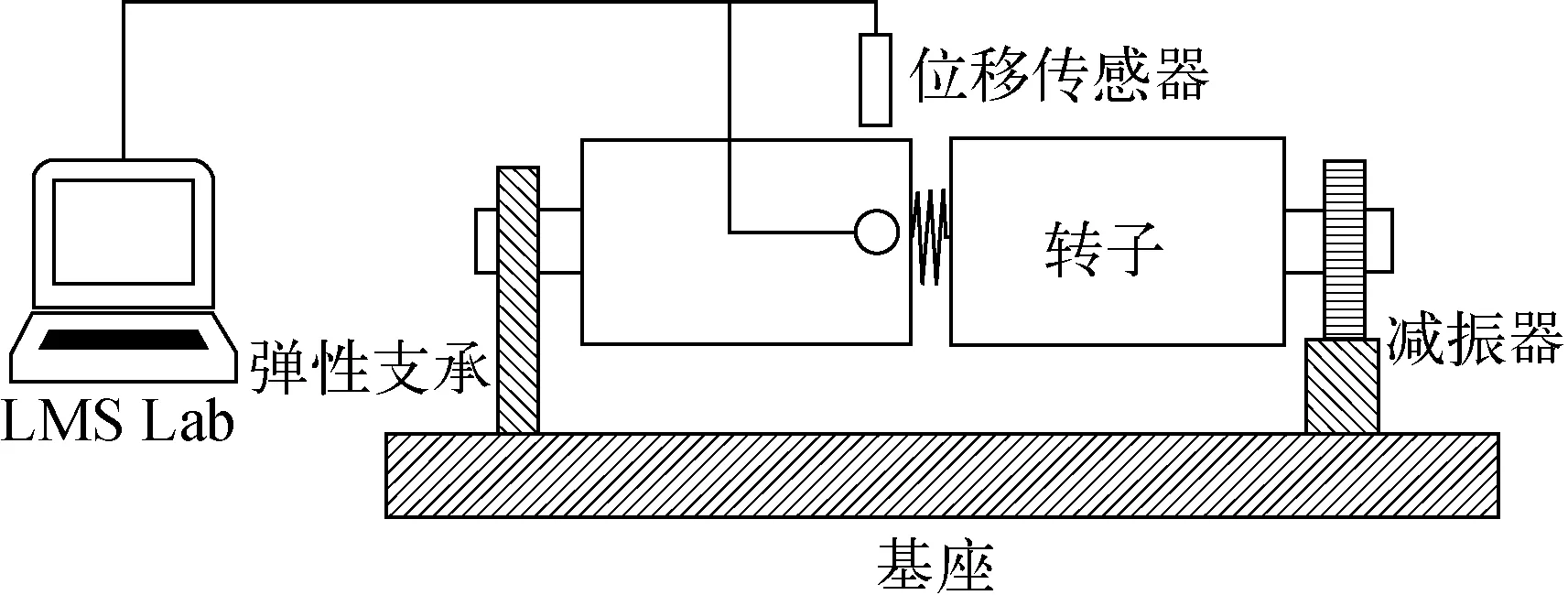
图3 试验测试平台Fig.3 Experiment set-up

3 结果分析

在正式试验和相应的理论计算中采用的弹性支承刚度k1=450 N/m，减振器主刚度k2=5.5×104N/m、集中质量m3=0.02 kg、次刚度k3=650 N/m、阻尼系数c3=40 N·s/m，弯曲刚度C=1 600 N/rad。由于转子强度限制，实际试验中主要检测在0～800 Hz范围内是否失稳，超过800 Hz后的转速不在讨论范围内。

4个转子的升速试验结果列于表2。在进行理论计算前，需先判断出现进动的模态是转子一弯还是二弯。通过对比理论与试验结果发现，升速中出现进动的主要模态为转子一弯模态，因此在进行失稳转速计算时需采用转子一弯模态所对应的虚部系数。由表2可知，1、2、3号转子通过理论计算得到的失稳转速与试验结果较符合，2和3号的理论失稳转速与试验结果相差在5%以内，而4号转子的理论与试验结果相差较大，可能是转子在升速过程中内阻尼增大较多，已远超过静态下的内阻尼。结合转子一弯模态虚部系数大小和失稳转速可知，随虚部系数增大，失稳转速逐步下降，这一结论符合黏弹性转子发生失稳的定性结论。

表2 转子支承系统失稳转速和进动频率Table 2 Threshold speed and processing frequency of rotor support system

分析不同参数对转子升速过程中一弯模态阻尼比的影响。图4示出虚部系数对一弯模态阻尼比的影响。图5示出di=0时转速对一弯模态阻尼比的影响。由图4可见，不同转速下的一弯模态阻尼比随虚部系数的增大而线性减小，在虚部系数为25×10-6～30×10-6时，转速为150～250 Hz下的一弯模态阻尼比为负数，进入失稳区域，即在该支承参数下转子最高升速到150 Hz左右。由图4还可看出，不同转速下的一弯模态阻尼比差距较大，转速为450 Hz时最大，与图5中静止时一弯模态阻尼比随转速的变化规律一致，在转速为438 Hz时取得最大值。这是因为减振器为一维振动系统，在一弯模态频率与其共振频率相近时，出现进动后减振器处于共振状态，振动幅度最大，相应的阻尼效果最好。在实际中可根据进动时的一弯模态频率进行减振器参数匹配，以期达到最佳阻尼效果。

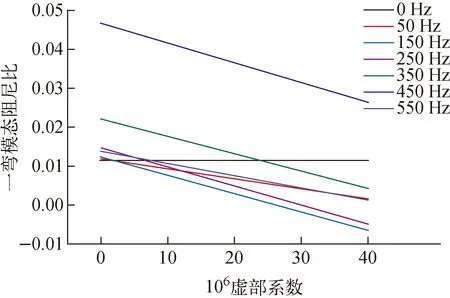
图4 虚部系数对一弯模态阻尼比的影响Fig.4 Effect of imaginary part coefficient on modal damping ratio of 1st bend

图5 di=0时转速对一弯模态阻尼比的影响Fig.5 Effect of speed on modal damping ratio of 1st bend at di=0

考虑内阻尼并计算不同减振器阻尼系数下一弯模态阻尼比随转速的变化，如图6所示。转速为400 Hz时一弯模态阻尼比随阻尼系数的变化如图7所示。由图6可看出，在阻尼系数为10 N·s/m时一弯模态阻尼比随转速的增大迅速下降，失稳转速约为150 Hz，阻尼系数增大到20 N·s/m后失稳转速约为600 Hz，随阻尼系数继续增大，失稳转速减小。在阻尼系数约为20 N·s/m时取得最高失稳转速，说明减振器在该阻尼系数下的阻尼性能最好，和图7所示规律一致。减振器是一维的弹簧阻尼系统，在进动频率即一弯模态频率与其共振相距较大时，处于过阻尼状态可获得最大阻尼性能，在进动频率接近其共振时，处于欠阻尼状态可获得最大阻尼性能，且存在最佳的阻尼系数。

图6 di=30×10-6时转速对一弯模态阻尼比的影响Fig.6 Effect of speed on modal damping ratio of 1st bend at di=30×10-6

图7 一弯模态阻尼比随阻尼系数的变化Fig.7 Change of modal damping ratio of 1st bend with damping efficient

由上述分析可知，转子虚部系数和减振器参数均会对升速过程中的失稳转速产生影响，因此以一弯模态阻尼比降低为0为界限作为失稳转速，得到不同虚部系数和减振器参数下的稳定域，如图8所示。图8中曲线代表不同阻尼系数所对应的失稳转速，空白部分为稳定域，阴影部分为失稳域。阻尼系数较小时同一个阻尼系数下会对应多个失稳转速，这并不矛盾，此时可认为阻尼系数是该转速下的失稳阻尼系数。由图8可看出，为保证转子不进入失稳域，则阻尼系数既不能太大，又不能太小，存在对应最高失稳转速的最佳阻尼系数，如图8a中约为20 N·s/m。如果可在升速中更改阻尼系数，则在图8b中随转速实时地降低阻尼系数可达到最高的失稳转速650 Hz。对比图8a、b可知，在同样的阻尼系数下，虚部系数越小则对应的失稳转速越小，如阻尼系数在20～40 N·s/m范围内的最小失稳转速约为650 Hz，而虚部系数较大时的最小失稳转速约为450 Hz，虚部系数对大和小阻尼系数时的失稳转速影响很大。对比图8b、c可知，提高减振器阻尼刚度可有效扩大稳定域的范围，提高失稳转速，但对于小阻尼系数下的失稳转速影响较小。