基于Beam-based近场动力学模型的材料冲击响应研究

刘 宁,王 帅,胡梦凡

(南京理工大学 机械工程学院,江苏 南京 210094)

用传统数值方法研究陶瓷装甲、混凝土工事等抗弹材料侵彻毁伤问题时,还不能提供完整的冲击破坏图像对冲击破坏过程给予动力学一致的分析,限制了结构防护的性能优化和评价。材料冲击破坏是一个裂纹形成、扩展、分叉直到最终破碎的复杂过程,经典连续介质力学理论在处理这种高度非线性和不连续性问题时具有一定的局限性,主要难点在于经典连续理论的数学模型是基于连续性假设下的包含空间导数的偏微分方程,一旦所研究的问题出现损伤、裂纹扩展、分层、断裂和穿透等不连续问题时则不存在位移偏导数,从而出现求解困难。

近年来一种新兴的基于非局部思想的近场动力学方法(Peridynamics,PD)从根本上解决了传统数值方法面临的求解困难,该方法已在模拟裂纹萌生、扩展、分离等不连续问题时表现出了独特的优势[1-2]。PD理论与经典连续介质力学最大的区别在于,PD方法使用空间积分方程来描述物质力学行为,而经典连续介质力学是基于位移的导数建立运动方程。PD理论的这一特征表明,材料域内任意位置的损伤的萌发和扩展是自发产生的,并且可沿任意路径进行,而不需要特别引入任何裂纹扩展准则[3]。

近场动力学理论体系中键基模型(bond-based PD)得到了广泛应用[4-5],但常规键基模型只考虑了物质点间的轴向力作用,仅有一个“材料常数”,导致了对材料泊松比的限制,如平面应力问题材料泊松比为1/3,三维问题泊松比限制为1/4,制约了键基近场动力学模型的应用范围。本文基于有限元Euler-Bernoulli梁单元模型思想[6-9],提出一种新型Beam-based近场动力学本构关系,突破常规键基近场动力学模型对材料泊松比的限制,通过算例验证新型PD模型对冲击动力学问题的适用性。

1 Beam-based PD模型

1.1 Bond-based PD基本理论

PD理论将物质体系看作由众多物质点构成,每个物质点具有确定的体积和密度,空间域Ω内的物质点x与其周围δ范围内的物质点x′∈Ω:‖x′-x‖≤δ存在相互作用力f,如图1所示,在任意时刻t,物质点x的运动方程为

(1)

式中:ρ为物质密度,u为物质点x的位移,e为体力密度,H代表了物质点x的近场邻域范围。

定义参考构形中物质点x与x′之间相对位置矢量ξ和相对位移矢量η分别为

ξ=x′-x,η=u′-u

(2)

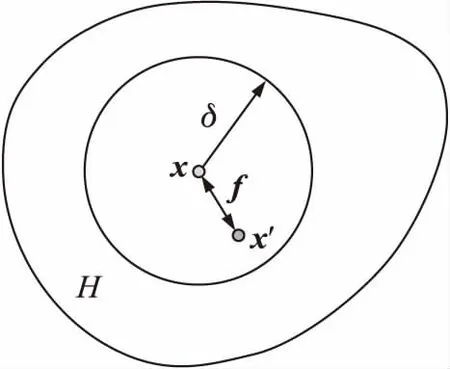
图1 PD理论模型

对于Bond-based PD模型,式(1)中物质点间的相互作用力f可以写为

(3)

式中:c为材料微弹性模量,可看作近场动力学理论中的“材料常数”;s为物质点之间键相对伸长率:

(4)

通过PD理论中应变能密度与经典弹性力学中应变能密度的等价关系[5],可推导出PD微弹性模量c,如平面应力问题微弹性模量:

(5)

式中:E为弹性模量;ν为泊松比,且为1/3,三维问题的泊松比限制为1/4,固定的泊松比限制了Bond-based PD模型的应用范围和求解精度。

在近场动力学中,某物质点的破坏程度用近场域内与该粒子有相互作用的键的断裂比例表征:

(6)

式中:μ为物质点之间键是否断裂的判据,即

(7)

式中:s0为键的临界伸长率。μ=1,表示物质点之间键未发生断裂;μ=0,表示键已断裂。

1.2 Beam-based PD模型的构建

基于有限元Euler-Bernoulli梁单元模型,在Bond-based PD模型的基础上加入了物质点间相对转动效应,建立了新型Beam-based PD模型,物质点间作用力由轴向力密度f1与切向力密度f2两部分构成,如图2所示,(x,x′)为初始构形,(y,y′)为现时构形。

Beam-based PD本构方程可以表示为

f=CS

(8)

式中:C为微弹性模量矩阵,可通过应变能密度等效方法推导;S为物质点相对伸长率矢量。在小变形情况下,参考有限元Euler-Bernoulli梁单元模型,将物质点相对伸长率矢量S进行泰勒展开和线性化处理:

(9)

式中:u1,u2,u′1,u′2分别为物质点变形前后轴向和切向位移矢量,r为物质点间相对位置矢量。

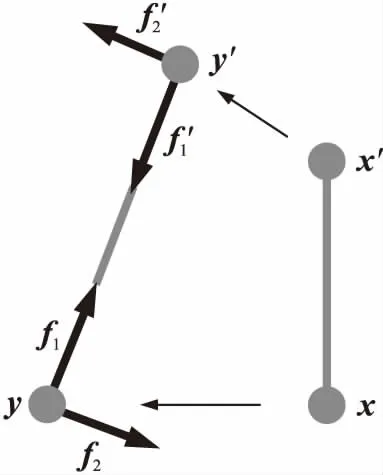
图2 梁模型物质点运动

1.2.1 二维Beam-based PD模型

二维情况下Beam-based PD本构函数可写为

(10)

式中:c1,c2分别为轴向和切向微弹性模量。

由式(9)可得物质点间轴向力与切向力表达式:

(11)

在二维笛卡尔坐标系下,物质点间轴向相对位移与切向相对位移可通过物质点坐标相对位移分量表示,如图3所示。

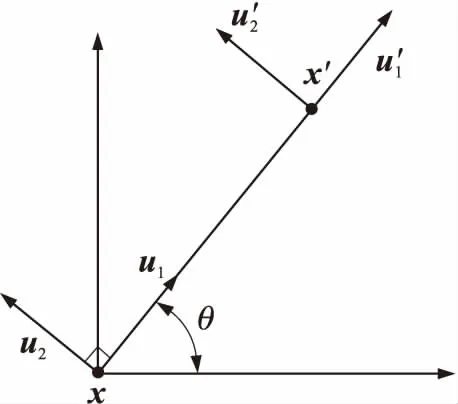
图3 二维梁模型物质点位移分量示意图

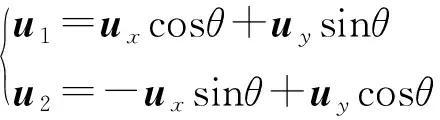
(12)

将式(12)带入式(11)可得:

(13)

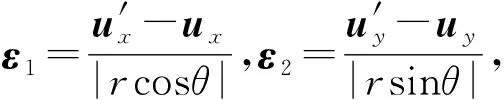
物质点间“梁单元”具有的微势能为

(14)

物质点x的应变能密度为

(15)

同时,在弹性力学中,平面应力问题的应变能密度为

(16)

根据应变能密度等效法,由式(15)、式(16)可得Beam-based PD模型轴向微弹性模量c1与切向微弹性模量c2:

(17)

写成矩阵形式:

(18)

式(17)中c1与c2为2个相互独立的PD常数,其中c1>0,c2≥0。可见对于平面应力问题,Beam-based PD模型的泊松比取值范围为(-1,1/3],大大扩展了传统键基PD模型的应用范围。

同理,可推导平面应变问题中Beam-based PD模型微弹性模量矩阵:

(19)

式中的泊松比范围为(-1,1/4]。

1.2.2 三维Beam-based PD模型

三维情况下Beam-based PD本构方程可写为

(20)

写成分量形式:

(21)

三维条件下物质点间“梁单元”微势能为

(22)

积分可得三维PD应变能密度:

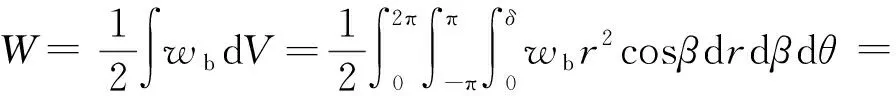
(23)

而经典弹性力学中三维应变能密度为

(24)

通过应变能密度等效方法,可得三维Beam-based PD模型微弹性模量:

(25)

写成矩阵形式:

(26)

式中:c1>0,c2≥0,三维Beam-based PD模型泊松比范围为(-1,1/4]。

2 数值方法

2.1 离散方程

将计算域进行离散,运动方程式(1)的离散形式可表示为

(27)

式中:i表示当前物质点,n为时间迭代步数,Vj为当前物质点i的邻域内物质点j的体积。

2.2 PD冲击接触算法

将冲击弹丸视为刚体,在冲击过程中弹丸不断把被冲击材料物质点从其运动轨迹上排挤开,如图4所示,受排挤物质点速度为

(28)

(29)

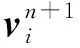
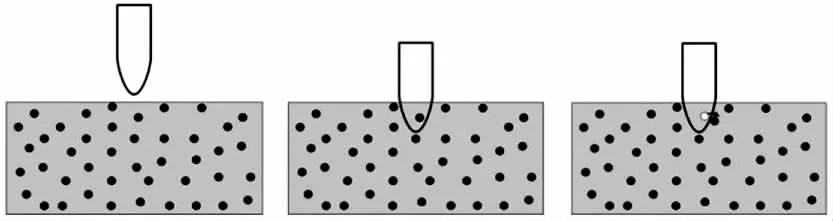
图4 刚性体冲击接触模型

3 算例研究

3.1 平板冲击

图5为刚性圆盘冲击矩形板模型[10],圆盘质量m=1.57 kg,直径D=50 mm,以速度v0=32 m/s冲击无约束矩形板上边缘中间位置,矩形板长l=200 mm,宽b=100 mm,厚度d=9 mm,密度ρ=8 000 kg/m3,弹性模量E=191 GPa,泊松比ν=1/3。采用Beam-based PD模型计算圆盘冲击过程,离散物质点间距Δx=1 mm,近场邻域范围δ=3.015dx,时间步长Δt=0.1 μs。

图6为不同时刻矩形板内部应力波云图,由图可见,在圆盘冲击矩形板后,应力波以冲击点为圆心,以半圆形辐射状向周围传播,应力波传播到左、右边界和底部边界时发生反射,多次反射后形成了复杂的应力分布特征,但在整个冲击过程中矩形板仅发生弹性形变,没有发生破坏。

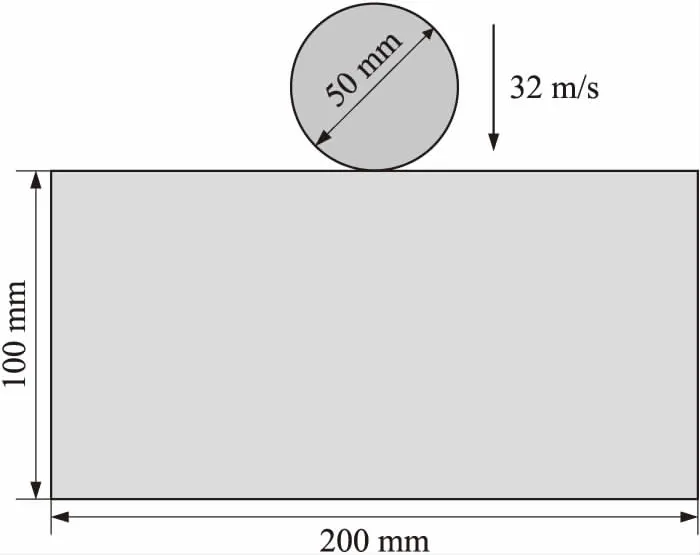
图5 圆盘冲击矩形板模型

图6 矩形平板应力波传播云图

为了验证Beam-based PD模型对不同泊松比材料的适用性,进一步计算了泊松比ν=1/4时矩形板中心的冲击响应,作为对比同时给出了有限元计算结果,如图7所示。

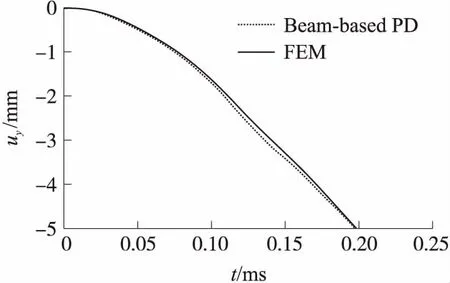
图7 泊松比为0.25时中心点位移变化曲线

由图7可见,本文模型计算结果与有限元结果吻合较好,验证了本文模型的正确性,新型PD模型有效拓展了Bond-based模型的应用范围。

3.2 三维Kalthoff-Winkler冲击模型

Kalthoff-Winkler冲击试验是用刚性圆柱弹丸冲击带有对称预置裂纹的马氏体时效钢靶板,观测裂纹的扩展过程,包括裂纹扩展方向和扩展速度等[11]。试验结果表明,圆柱体撞击靶板时产生冲击压缩波,使得裂纹从裂尖处开始扩展,产生Ⅱ型裂纹,最终形成的裂纹与预制裂纹夹角约为70°。Kalthoff-Winkler冲击试验已成为研究材料动态断裂本构模型和数值方法的经典验证算例。Kalthoff-Winkler冲击模型如图8所示,材料参数如表1所示。图中,圆柱直径D=50 mm,冲击速度v0=32 m/s,靶板长度l=200 mm,厚度d=9 mm,宽度b=100 mm,预制裂纹长l0=50 mm,间距h=50 mm,裂纹宽度a=1.5 mm。

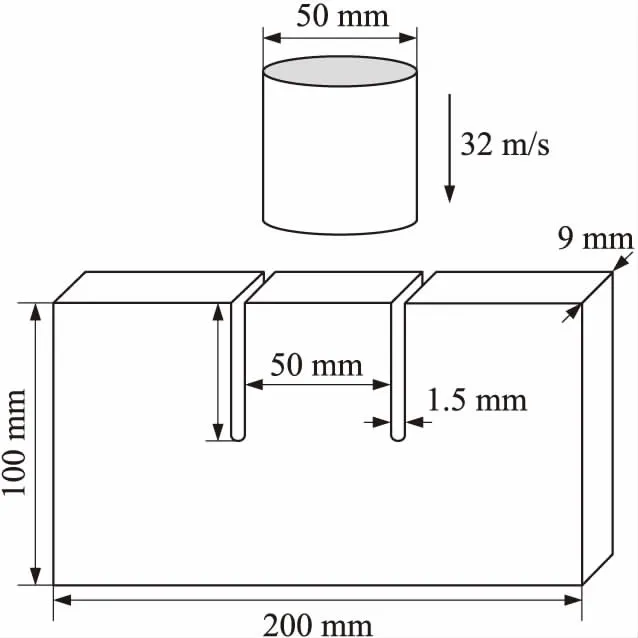
图8 Kalthoff-Winkler试验几何模型

表1 靶板材料参数

E/GPaρ/(kg·m-3)ν1907 8300.3

采用Beam-based PD模型模拟Kalthoff-Winkler冲击试验,取物质点间距Δx=1 mm,近场邻域δ=3.015dx,材料临界伸长率s0=0.01,时间步长Δt=0.58 μs。

图9为Beam-based PD模拟的裂纹扩展过程,裂纹从预制裂纹尖端开始扩展,几乎沿一条直线对称扩展至靶板左、右两侧边缘,裂纹扩展方向与预制裂纹夹角大约为68.3°。图10为文献[12]给出的Kalthoff-Winkler冲击试验结果和扩展有限元仿真结果。由图可见,本文模拟的裂纹扩展过程与试验值吻合较好。

众所周知,传统有限元法难以直接模拟材料破坏过程,而改进的扩展有限元法需要人为设置合适的破坏准则才能模拟裂纹扩展。本文建立的Beam-based PD模型不仅扩展了传统键基模型的适用范围,还能够模拟裂纹的自然萌生和自发扩展过程,无需任何外部干预,在处理材料冲击破坏问题时显示出巨大的优势,为冲击动力学研究提供了新的研究手段。

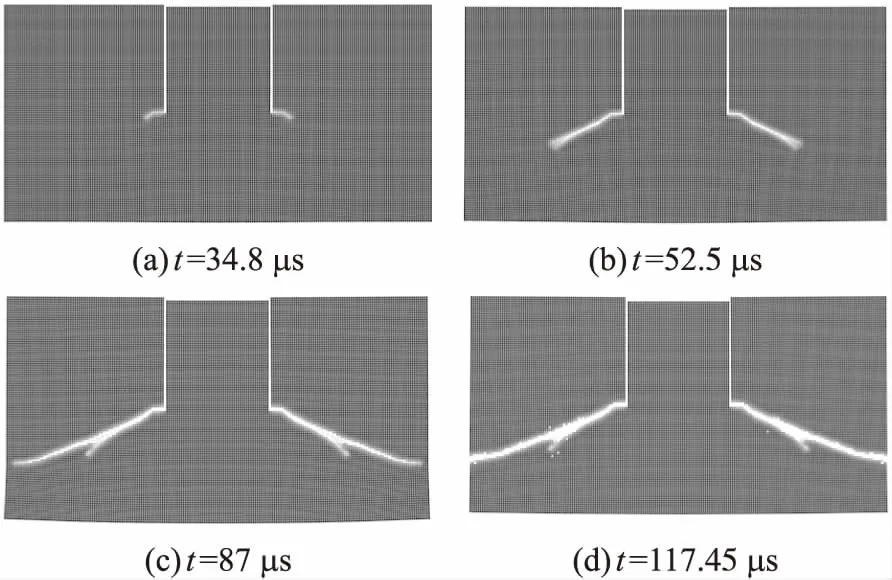
图9 Beam-based PD模拟的裂纹扩展过程

图10 Kalthoff-Winkler试验及扩展有限元结果[12]

4 结束语

本文针对常规Bond-based近场动力学模型对材料泊松比的限制,借鉴有限元Euler-Bernoulli梁单元模型,在Bond-based模型的基础上加入了物质点间相对转动效应,建立了新型Beam-based PD本构模型,有效拓展了泊松比范围。圆盘冲击矩形板模拟结果表明,泊松比对动态冲击响应具有重要影响,本文模型能够正确反映材料泊松比效应。模拟了Kalthoff-Winkler靶板冲击过程,裂纹扩展角度和裂纹扩展速度与试验结果吻合较好,新型Beam-based PD模型能以材料真实泊松比准确计算冲击载荷作用下材料的变形和破坏过程。本文模型对认识脆性材料冲击破坏的复杂物理机制具有明显优势,为冲击动力学问题研究提供了一条新的技术途径。