高速射弹表面超空泡形成特性的数值计算分析

胡雨博,余永刚

(南京理工大学 能源与动力工程学院,江苏 南京 210094)

为应对现代海战的需要,大量弹箭武器的打击范围已经从空中、水面延伸到水下。水下高速弹箭武器由于隐蔽性好、突击能力强,已成为各国海军武器装备的发展重点。由于水的密度远大于空气密度,常规弹丸在水下运动时受到的阻力约为空气中的800倍,因此常规弹丸在水中航行时速度迅速衰减[1-2]。为了减小弹丸的速度衰减,获得更高的存速,如何显著降低弹丸水下运动的阻力成为了研究的重点。

超空泡技术[3-4]是一种革命性的减阻方法,其显著的减阻效果对水下航行体的研制和开发产生了巨大的影响。施红辉等[5]对6 mm口径钝头体射弹在30～40 m/s速度范围内的水下运动过程进行了实验研究,分析了水深对超空泡形态和弹丸阻力系数的影响,及超空泡与自由面之间的相互作用。路丽睿等[6]对不同头型的9 mm射弹低速斜入水过程进行了试验研究,得到了射弹头型对入水空泡、运动速度和阻力系数的影响。张木等[7]针对带圆盘空化器的多锥体射弹进行了斜入水试验,分析空化数变化和结构参数变化对多锥体射弹阻力系数的影响。Kinnas等[8]应用基于速度势的边界元方法,通过数值模拟得到了翼型结构的空泡形状。Kunz等[9]对超空泡的流场特性做了大量的数值仿真,分析了水下航行体表面的压力分布和空泡形态的尺寸。Kirschner等[10]利用细长体理论和边界元方法对超空泡航行体进行了数值计算,在超空泡的形态模拟和超空泡的控制方面取得了一定成果。Neaves等[11]采用自适应网格技术,对超声速和跨声速超空泡射弹运动进行了数值模拟,研究了射弹高速入水时的模型总阻力和表面压力分布。王柏秋等[12]采用动网格技术模拟了直径2～4 mm的圆柱体在超空泡状态下的自然减速运动过程,得到了该过程中超空泡形态及模型阻力系数的变化规律。金大桥等[13]对15 mm口径的水下射弹进行了数值模拟,研究了空化数在0.01～0.2范围内时结构参数变化对自然超空泡形态特性和减阻特性的影响。易文俊等[14-15]针对30 mm口径的水下高速运动弹丸进行了数值模拟,研究了空化器结构及弹丸结构对自然超空泡形态特性及减阻特性的影响。综上所述,国内外学者针对较小口径射弹超空泡状态下的空泡形态以及阻力系数进行了大量的试验研究和数值模拟,但是对于空泡在高速运动的较大口径弹丸表面的形成过程和空泡发展速率的变化过程研究较少。

本文基于均质平衡多相流理论,建立了水下高速射弹超空泡形成过程的数理模型,并针对不同速度的76 mm射弹进行了数值模拟。对超空泡在弹丸表面形成的非稳态过程进行了研究,分析了射弹速度变化对超空泡形成过程、空泡发展速率的变化及阻力系数衰减过程的影响。研究结果可为超空泡射弹火炮武器的射弹流体动力外形设计提供参考。

1 数值计算模型

1.1 连续性方程与动量方程

高速射弹在水中航行时,弹体表面将形成超空泡。为了描述超空泡形成特性,本文基于均质平衡多相流理论,将弹体外的流动介质看作密度可变的单相流体,即水蒸气与水的混合物。假设混合流之间不存在分界面,整个混合物允许相互对流,各相共享同一压力场和速度场,由此可得到二维轴对称的连续性方程和动量方程。

混合相连续性方程:

∂ρm/∂t+∂(ρmvz)/∂z+∂(ρmvr)/∂r+(ρmvr)/r=0

(1)

混合相动量方程:

(2)

式中:vz,vr分别为柱坐标系下的速度分量;p为流场压力,下标m表示混合相,·v=∂vz/∂z+∂vr/∂r+vr/r;ρm为混合物的密度,μm为混合物的动力黏度,由水蒸气和水的体积加权平均得到:

ρm=φvρv+(1-φv)ρl
μm=φvμv+(1-φv)μl

式中:ρv,ρl分别为水蒸气和水的密度;μv,μl分别为水蒸气和水的动力黏度;φv为混合物中水蒸气的体积分数。

1.2 空化模型

弹体表面空化过程中水蒸气相的连续性方程:

(3)

式中:wv=φvρv/ρm,为水蒸气的质量分数。

相间质量传输率R可用空化模型来模拟:

R=Re-Rc

(4)

式中:Re为水蒸气的生成率,Rc为水蒸气的凝结率。

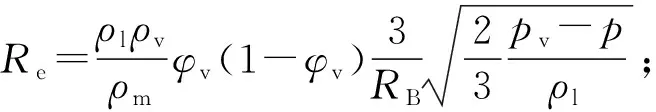
1.3 简化Tait方程

当Ma>0.3时,需要考虑液体的可压缩性。Tait方程是通过采用非线性回归的方法,对能够反映压力-速度-温度三者关系的试验数据进行拟合,得到的液体状态方程。为了简化模型,不考虑流场温度变化对物性参数的影响,采用忽略温度修正项的简化Tait方程。简化Tait液体状态方程为

(ρ/ρ0)κ=K/K0

(5)

式中:K=K0+κΔp,Δp=p-p0。

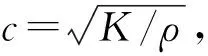
1.4 空化数与阻力系数模型

空化数是描述空化起始状态的一个无因次参数,其定义为:σ=(p∞-pv)/(0.5ρlv2),式中:p∞为环境压力,ρl为流体密度,v为弹丸速度。

弹丸表面产生空化现象后,由于弹体表面流体介质的密度减小,弹丸表面摩擦阻力降低,从而达到良好的减阻效果,因此,通过观测摩擦阻力与摩擦阻力系数的变化,能够反演空泡的发展过程。摩擦阻力Ff与摩擦阻力系数Cf计算公式如下:

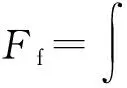
(6)

式中:黏性切应力τw=μm(dv/dr)r=0,Cf=Ff/(0.5ρlv2S),其中:S为特征面积,这里取弹丸圆柱部横截面积。

2 模型验证

搭建水下枪发射系统,试验总体装置由水箱、射击平台、脉冲点火源和高速录像系统四部分组成。试验射弹模型结构:圆盘空化器直径Dn=6.6 mm,弹丸头部长Ln=11.2 mm,弹丸圆柱部长Lc=42.8 mm,弹丸全长Lb=54 mm,弹丸最大截面直径Dm=12.7 mm。水下射击试验采用密封式发射,试验时,利用脉冲点火电源点燃燃烧室内火药,采用FASTCAM-Ultima APX高速数码相机记录弹丸表面超空泡形态,其最大分辨率为1 024×512,频率为4 000 s-1。通过高速录像图片得到的射弹初速为383.5 m/s。利用上述数学模型,以相同的射弹结构以及试验工况,对射弹表面超空泡形态进行数值模拟。图1为1.75 ms时刻试验与计算得到的弹丸表面超空泡形态,其中实线为数值模拟结果,虚线为试验结果。由图可知,数值模拟与试验得到的弹丸表面超空泡形态基本相同。

图1 1.75 ms时刻超空泡轮廓

以弹丸顶部中点为原点,轴向为x轴方向,径向为y轴方向,t=1.75 ms时弹丸表面超空泡轮廓图,如图2所示。由图可知,数值模拟与试验得到的弹丸表面超空泡轮廓几乎重合,平均误差仅为1.1%。

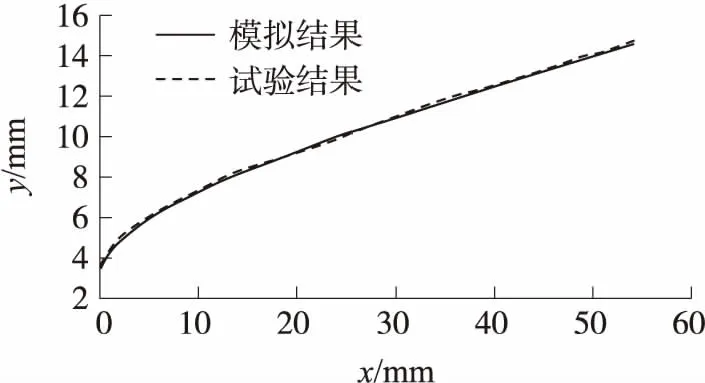
图2 弹丸表面超空泡轮廓试验与模拟对比

根据文献[7]中的试验,以500 m/s和900 m/s的弹丸初速作为速度入口,以101 325 Pa的压力作为压力出口,对30 mm带圆盘空化器的航行体进行数值模拟,将计算得到的阻力系数CD与试验测量值进行对比,结果如表1所示,表中,e为误差。

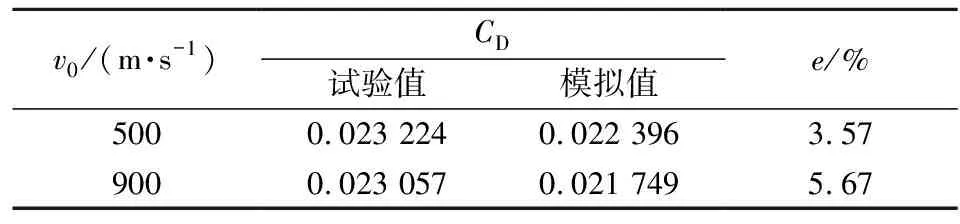
表1 阻力系数的试验值与模拟值的对比

由表1可以看出,通过模拟与试验得到的弹丸阻力系数基本相同。综上所述,计算结果与试验结果吻合较好,说明本文建立的数值计算模型基本合理。据此可以以相同的数学模型和计算方法对76 mm口径弹丸超空泡的形成过程进行数值预测。

3 数值预测及分析

在以上模型验证的基础上,针对设计的76 mm高速射弹在水中形成超空泡的过程进行数值预测。弹丸简化结构如图3所示,其中,圆盘空化器直径Dn=18 mm,弹丸头部长Ln=238 mm,弹丸圆柱部长Lc=132 mm,弹丸全长Lb=370 mm,弹丸最大截面直径Dm=76 mm。

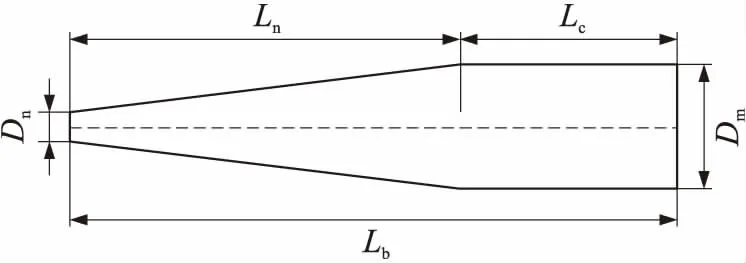
图3 76 mm口径弹丸模型结构

考虑到模型和流场都是轴对称的,建模时取对称体的一半进行网格划分和计算。网格采用结构性网格,并对弹丸表面附近区域进行局部加密。分别取网格总数为153 919,218 806,310 350,进行网格无关性验证,对v=900 m/s(σ=0.000 49)时不同网格数下的阻力系数进行数值模拟,得到的阻力系数分别为0.075 3,0.069 3,0.067 8。可以看出网格总数为153 919和218 806时的阻力系数与网格总数为310 350时的阻力系数相差分别为11.06%和2.21%,因此出于提高计算效率的考虑,网格总数选择为218 806。利用Fluent软件,采用二维非定常求解器,边界条件设置为左侧边界为速度入口,上、下边界和右侧边界为压力出口,如图4所示,模型壁面为无滑移条件。数值模拟中,采用基于压力的隐式算法求解,对湍流模型采用标准k-ε模型,采用非平衡壁面函数处理近壁面区域,应用PISO算法求解压力和密度的耦合。为了避免一阶迎风格式可能引起的假扩散问题,对流相的离散采用二阶迎风格式。为了研究速度变化对超空泡形成过程的影响,以500～1 300 m/s(σ=0.001 59～0.000 23)为速度入口,以水深10 m的压力201 325 Pa为压力出口进行数值模拟。

图4 边界条件及网格划分

图5为v=800 m/s(σ=0.000 62)时弹丸表面超空泡的形成过程。由图可见,在0.1 ms时弹丸头部、圆柱部和尾部3个区域都产生了空化现象。在弹丸头部前端和尾部,水蒸气迅速产生并积聚形成局部空泡,但在圆柱部前端只产生了少量水蒸气。随后,圆柱部表面产生空化现象的区域迅速增大,在0.6 ms时已包裹整个圆柱部,但是水蒸气积聚效果不佳,导致圆柱部区域的水蒸气含量较低,无法称为形成局部空泡。这个过程中弹头部和弹尾部的局部空泡也在逐渐发展。当弹丸头部全部被空泡包裹时,3个产生空化现象的区域互相联通,弹丸圆柱部区域水蒸气含量开始再次增加,使圆柱部区域逐渐被空泡包裹,2.2 ms时弹丸全部被水蒸气包裹,弹丸表面形成超空泡。

图6显示了v=800 m/s时弹丸表面不同位置的混合物中水蒸气的体积分数φv随时间的变化规律,其中,x表示距弹头部顶点的轴向距离。x<238 mm属于弹头部区域,x>238 mm属于弹丸圆柱部区域,x=238 mm为弹头部区域和弹丸圆柱部区域的分界点。由图4可见,空化现象在弹丸头部区域和弹丸圆柱部区域的发展过程有所不同。在弹头部区域,弹丸表面各点依次产生空化现象,其水蒸气含量近似呈线性上升,当φv≥0.5时[5],可认为形成空泡,随后水蒸气含量继续升高,直至0.9以上。

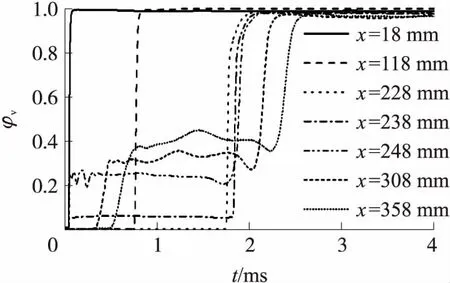
图6 混合物中水蒸气体积分数变化曲线

空化现象的发展在弹丸圆柱部区域可分为3个阶段:第一阶段,弹丸圆柱部表面各点依次产生空化现象,各点处产生水蒸气后的水蒸气体积分数φv迅速提高至0.4左右,并且越靠近弹丸尾部的点水蒸气含量越高。这是因为弹丸圆柱部表面各点处的水蒸气由两部分组成:一部分是由空化产生并在原地积聚的水蒸气,另一部分是由上游各处产生并顺流而下的水蒸气。因此,越靠近弹丸尾部的位置混合物中水蒸气含量越高。

圆柱部表面各点经过第一阶段的快速积累后进入第二阶段,各点水蒸气含量进入平台期,在此期间水蒸气含量略有波动但总体而言几乎保持不变,这是因为弹丸圆柱部各点的部分水蒸气会向下游流去。由图6可见,当点x=238 mm处处于平台期期间,水蒸气含量仅为不到0.1。这是由于流体经过弹丸头部区域后,弹丸圆柱部区域的空泡脱体点不在圆柱体的前缘而是略微靠后。当点x=228 mm处水蒸气含量大于0.8后(tp=1.81 ms),点x=238 mm处的平台期结束,水蒸气含量开始再次提升。这是由于1.81 ms后有弹头部区域的水蒸气向圆柱部区域流动。由此可知,弹丸头部全部被空泡包裹后,圆柱部表面各点依次结束平台期。不同射弹速度下水蒸气含量平台期持续时间如图7所示。由图可见,平台期持续时间会随着弹丸速度的增加不断变短。

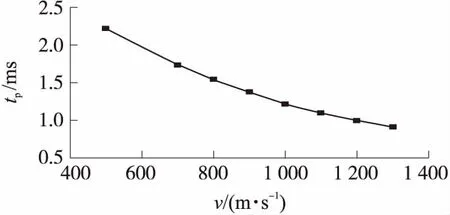
图7 不同速度时平台期持续时间

第二阶段平台期结束后,第三阶段中圆柱部表面各点的水蒸气含量开始再次迅速增加,形成空泡后,水蒸气含量继续升高至0.9以上。由于弹丸圆柱部区域水蒸气含量上升的2个阶段所需时间非常短,所以平台期的持续时间可以近似看成超空泡形成所需的时间。从图7中拟合出平台期持续时长随弹丸速度变化的经验公式,可用作估算不同速度下超空泡形成所需时间,即

(14)

式中:v为弹丸速度(m/s),t为时间(ms)。

图8为不同射弹速度下弹头表面已形成空泡的位置随时间的变化曲线,此曲线斜率可表征空泡的发展速率。由图可见,曲线呈非线性变化,各条曲线的斜率在弹头前端最大,随后逐渐减小,说明在弹头前端空泡的发展速率最快,随后减小。射弹速度越快,空泡包裹弹头部所需时间越短。为了进一步考察空泡发展速率在弹头部表面的变化过程,对图8中各曲线求导,可得出不同射弹速度下弹头表面不同位置的空泡发展速率vc,如图9所示。由图可见,弹头表面空泡发展速率的变化过程可以分为2个阶段,即由一个快速的线性衰减阶段逐渐过渡到一个近似呈缓慢线性衰减的阶段,在第一阶段中空泡发展速率将衰减60%左右。射弹速度越快,空泡发展速率越高,第一阶段中衰减得越快,衰减幅度随射弹速度变化从59.84%逐渐增加至65.09%,而第二阶段中空泡发展速率的衰减速度则几乎不变。

图8 不同弹丸速度时弹头部空泡发展过程

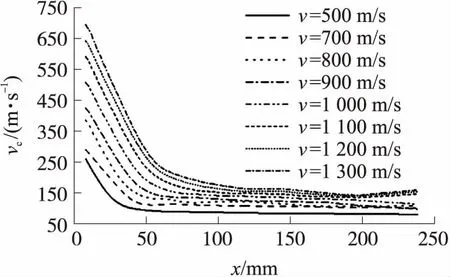
图9 不同弹丸速度时弹头表面不同位置空泡发展速率

图10显示了弹头部空泡发展速率变化过程的第一阶段终点位置(A)在弹头表面的变化。由图可见,随着射弹速度的变化,A点位置在弹头表面1/4处左右很小的区域内移动(x=37～58 mm),并随着射弹速度的增加逐渐向弹头尾部方向移动。

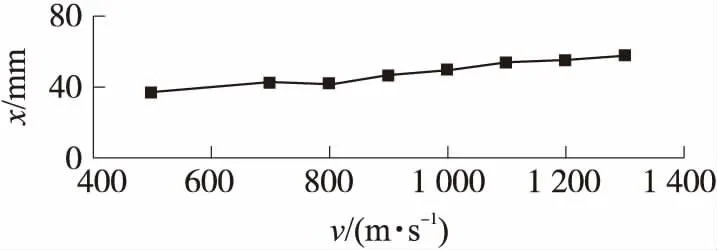
图10 弹头部空泡发展第一阶段终点所在位置随速度的变化曲线

图11为不同射弹速度时圆柱部表面已形成空泡的位置随时间的变化曲线。由图可见,曲线近似呈线性变化,射弹速度越快,曲线斜率越大。为了更仔细地研究空泡发展速率在圆柱部表面的变化过程,对图11中各曲线求导,可得出不同射弹速度时圆柱部表面不同位置的空泡发展速率vc,如图12所示。由图可见,圆柱部表面空泡发展速率的变化可以分为2个阶段,第一阶段空泡发展速率迅速衰减,第二阶段空泡发展速率的衰减速度明显降低。射弹速度越快,空泡发展速率整体越高,第二阶段中衰减得也越快,但第一阶段中衰减速度变化不大。

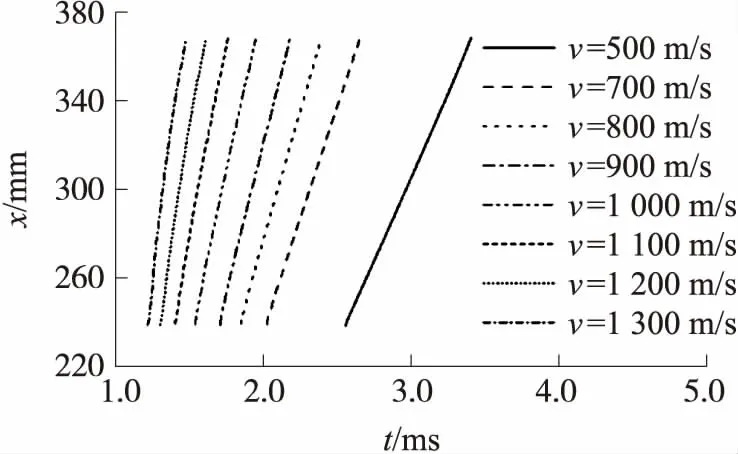
图11 不同弹丸速度时圆柱部空泡发展过程

图13显示了圆柱部空泡发展速率变化的第一阶段终点位置(B)在圆柱部表面的变化。由图可见,随着射弹速度的变化,第一阶段终点位置在圆柱部表面很小的区域内变化(x=244 mm左右),其位置随着射弹速度的增加先向弹尾方向移动,当速度高于900 m/s后,又向圆柱部前端方向移动。

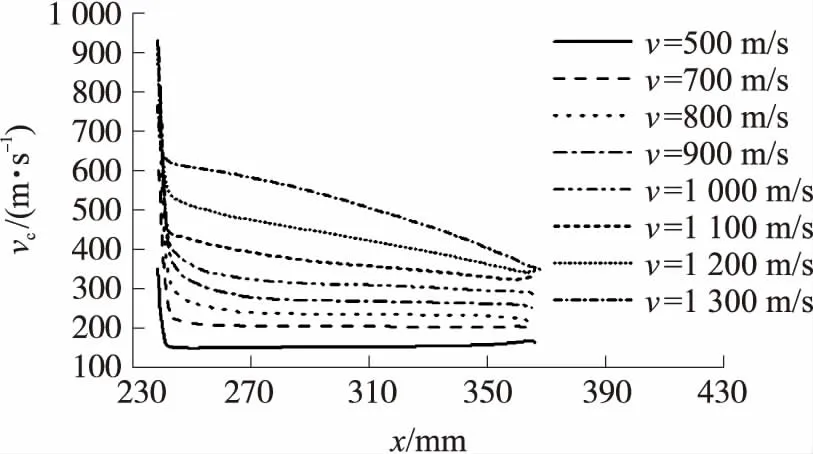
图12 不同弹丸速度时圆柱部表面不同位置空泡发展速率

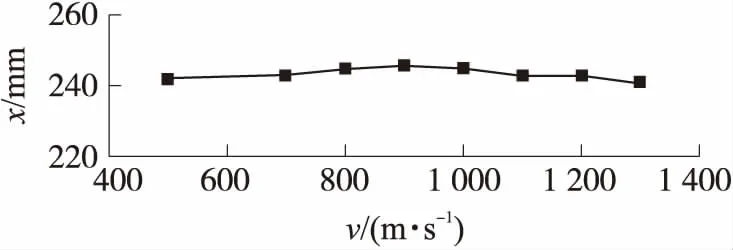
图13 圆柱部空泡发展第一阶段终点所在位置随速度的变化曲线

图14显示了不同射弹速度下弹丸表面摩擦阻力系数与时间的关系,其中弹丸表面摩擦阻力由弹丸头部区域和弹丸圆柱部区域摩擦阻力两部分构成。由图可见,弹丸表面摩擦阻力系数的衰减大致分为3个阶段,与空化现象在圆柱部区域的发展特性相对应,即2个短时间的快速下降阶段,中间包含一个较长时间的平缓下降阶段。

图14 不同弹丸速度时摩擦阻力系数随时间的变化曲线

第一阶段中摩擦阻力系数衰减的原因有2个:主要原因是,在弹丸圆柱部产生空化现象的区域迅速增大,虽然没有形成局部空泡,但是降低了圆柱部表面混合物的密度,减小了圆柱部区域的摩擦阻力;另一个原因是,在弹丸头部产生了较小的局部空泡,降低了一部分弹丸表面摩擦阻力。第二阶段中弹丸圆柱部水蒸气含量在平台期中变化较小,因此圆柱部区域的摩擦阻力系数基本不变,而弹丸头部空泡的逐渐发展使弹丸头部的沾湿面积不断减小,弹头部区域摩擦阻力不断减小,因此弹丸表面摩擦阻力系数会较长时间地平缓下降。第三阶段摩擦阻力系数再一次短时间地快速下降,是因为此时弹丸头部已全部被空泡包裹,弹丸圆柱部水蒸气含量开始迅速提升,弹头部摩擦阻力系数基本不变,圆柱部摩擦阻力系数迅速下降,导致了弹丸表面摩擦阻力系数进一步迅速衰减。由图14可见,随着射弹速度的增加,摩擦阻力系数衰减的各阶段所需时间都有所减小,且摩擦阻力系数达到稳定时的值越小。当射弹速度提高到1 100 m/s后,速度继续增加,摩擦阻力系数达到稳定的时间几乎相同,且达到稳定时的值变化不大。

4 结论

本文针对76 mm高速射弹超空泡形成的非稳态过程进行了数值分析,可得出如下结论:

①水中高速射弹弹体表面不同部位空化过程特点不同。在弹头部区域,沿轴线方向各点依次产生空化现象,其水蒸气含量呈线性上升到0.9以上;在弹丸圆柱部区域,各点依次产生空化现象,且其水蒸气含量先迅速上升至0.3～0.4,随后进入平台期,待弹头全部被空泡包裹后,弹丸圆柱部水蒸气含量平台期结束,水蒸气含量再次上升直至0.9以上。空泡在弹丸头部是一次形成的,而在弹丸圆柱部是渐次形成的,当弹丸表面全部被空泡包裹时即形成超空泡。在一定范围内,射弹速度越快,平台期持续时间越短,超空泡形成得越快,超空泡形成时间满足指数型变化规律。

②空泡发展速率变化特性与弹体部位密切相关。在弹头部,其变化过程是由一个快速的线性衰减阶段逐渐过渡到一个近似呈缓慢线性衰减的阶段,空泡发展速率在第一阶段中将衰减60%左右。射弹速度越快,空泡发展速率越高,且在第一阶段中衰减得越快,衰减幅度也越大,衰减幅度最高可达65.09%;而第二阶段中空泡发展速率的衰减速度则几乎不变。随着射弹速度的变化,第一阶段终点位置(A)在弹头表面1/4处左右的区域内移动(x=37～58 mm),随着射弹速度的增加,第一阶段终点位置逐渐向弹丸尾部方向移动;在弹丸圆柱部,空泡发展速率的变化过程可以分为2个阶段,第一阶段空泡发展速率衰减迅速,第二阶段衰减速度则明显降低。射弹速度越快,空泡发展速率整体越高,第二阶段中衰减也越快,但第一阶段中衰减速度变化不大。随着射弹速度的增加,第一阶段终点位置(B)在圆柱部前端很小的区域变化(x=244 mm左右)。由此,为了缩短射弹表面超空泡形成所需时间,需要尽可能使位置A、B沿弹丸轴向向后移动。

③ 弹丸表面摩擦阻力系数呈非线性衰减,衰减过程分3个阶段,与空化现象在弹丸圆柱部发展过程的3个阶段相对应。射弹速度越快,阻力系数衰减得越快,达到稳定时的值越小。当速度提高到1 100 m/s后,再增大射弹速度,阻力系数达到稳定的时刻几乎不变,且达到稳定时的值变化也不大。