固定鸭舵修正弹非线性与非定常气动数值模拟

钱 龙,常思江,杨文龙,魏 伟

(1.南京理工大学 能源与动力工程学院,江苏 南京 210094;2.中国兵器工业试验测试研究院,陕西 华阴 714200;3.中国兵器工业第208研究所,北京 102202)

弹道修正弹是近年来国内外的研究热点之一[1-2],与常规榴弹相比命中精度高,与一般导弹相比成本较低,因此具有重要的军事和经济价值。在诸多弹道修正弹方案中,一类固定鸭舵修正弹由于其控制机构简捷、与原弹适配性好等特点,近年来受到广泛关注。所谓固定鸭舵修正弹就是指在常规弹药前端将引信部分替换为以鸭舵作为修正机构的精确制导组件,通过控制指令使其滚转角在空间中的方位固定,以实现弹道二维修正作用。

目前在二维弹道修正技术研究方面美国一直处于领先地位,在本世纪初就提出分阶段研发精确制导组件(PGK)即二维弹道修正引信方案,于2014年在大口径榴弹上成功地实装二维修正引信模块,并通过了产品的验收试验。相比而言,国内研究起步较晚,但近年来也开展了相关工作。在飞行动力学方面,常思江等[3]对固定鸭舵双旋弹进行了七自由度飞行动力学建模与仿真计算;吴映峰等[4]推导了固定舵匀速转动时攻角的强迫运动解,研究了此旋转稳定二维修正弹的飞行稳定条件;于剑桥等[5-6]研究了固定翼双旋弹的角运动特性和飞行稳定判据,得出了不同鸭舵安装角以及飞行速度对动力学分岔特性的影响。在弹丸的气动特性方面,纪秀玲等[7]研究分析了一定马赫数、小攻角范围内的纵向气动系数随鸭舵方位角的变化规律;郝永平等[8]利用流体力学和动力学软件联合仿真研究了不同横风大小下鸭舵的修正能力;朱少雄等[9]利用Fluent仿真研究了气动参数在小攻角范围内的变化规律;吴萍等[10]采用风洞实验研究了该弹气动特性在一定攻角下随马赫数及舵偏角的变化规律,徐辉雯等[11]研究了组件反旋和不旋的气动特性。

以往气动特性方面相关研究重点主要为:通过理论数值计算或者风洞实验给出气动系数,讨论其在多种不同工况下的变化趋势。但以往的理论计算多集中于小攻角范围内,并没有针对大控制力时弹丸飞行攻角较大的气动特性进行分析,且总体来看在真实运动模拟方面或者说在更为接近真实的条件下的数值计算的研究还较少。

因此,本文先利用计算流体动力学方法对固定鸭舵修正弹进行了多马赫数、较大攻角范围的气动数值计算,获得了该弹的非线性气动系数,然后提出一种考虑弹丸进动运动在内的非定常数值模拟方法,对弹丸包含角运动的气动力展开计算和分析。

1 数值方法及计算条件

1.1 数值方法与验证

修正弹头部、弹身具有不同的转速,故其气动计算采用动网格中的滑移网格技术。综合考虑计算资源、速度以及精度,本文采用Spalart-Allmara(SA)湍流模型、二阶迎风差分格式以及密度基隐格式对亚、跨、超声速下固定鸭舵修正弹的绕流场进行数值模拟。

为了对拟采用的方法进行验证,选取M483A1大口径弹为对象,进行气动力定常和非定常计算验证。如图1所示,图中C′1为法向力系数导数,C′2为俯仰力矩系数导数。

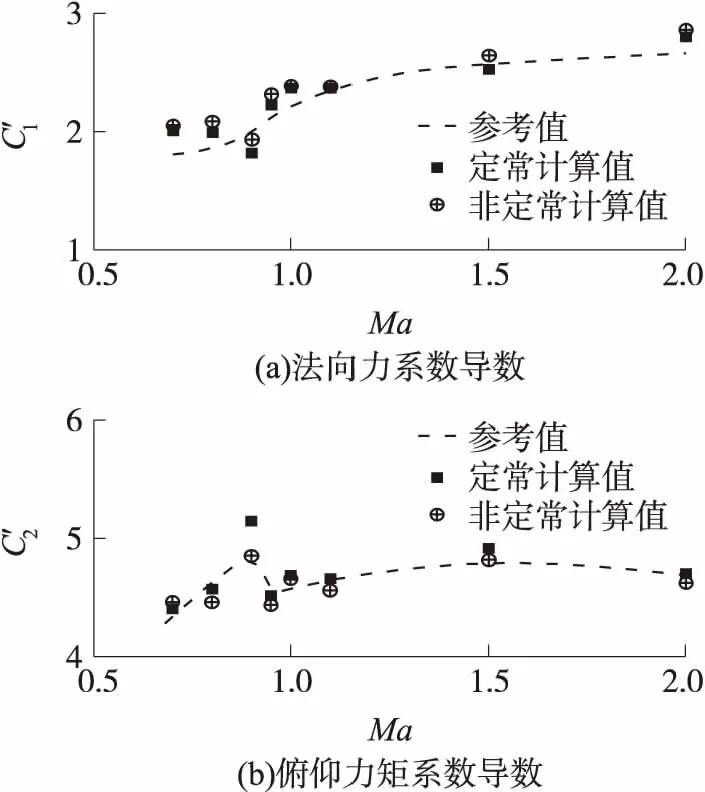
图1 气动参数随马赫数变化曲线

所得计算结果与文献[12]中由靶道实验提取的气动数据均值规律基本一致,且C′1误差小于10%,C′2误差小于6%,这表明拟采用的数值计算方法可行有效。

1.2 工况选取与网格划分

图2 固定鸭舵修正弹

考虑到弹丸实际飞行的马赫数区间,为研究弹丸的非线性气动特性,选取工况如下:

①工况1。定常工况,Ma=0.5,0.8,0.95,1.0,1.1,2.0,3.0;α=0°,2°,4°,8°,15°,20°。

弹丸在实际飞行中会存在快、慢圆运动。设计良好的弹丸在出炮口后快圆运动的幅值迅速收敛后几乎消失,而在全弹道慢圆运动为主,故在数值模拟中,可忽略快圆运动,仅考虑慢圆运动,据此设计工况3。

由于工况2和工况3为非定常计算,且头部、弹身具有不同转速,故计算采用滑移网格,将全流场分成三部分,分别为计算域1、计算域2和计算域3,并使用交接面(Interface)产生信息交互。弹体附近的网格和完整网格如图3和图4所示。具体实现工况3中所述运动的方法见后文3.2.2节。

图3 弹体附近流场边界网格

图4 整体流场边界网格

2 流场分析

为直观地体现弹丸周围流场的状态,选取典型的亚、跨、超声速流场图,分析其气动特性。

2.1 纵向流场

图5为在不同马赫数下且α=0°时的流场速度云图,图中舵面后上方的异常点是由于滑移网格在此发生了重叠,对计算结果并无影响。

由图5可以看到马赫波呈现不同状态下的应有规律:亚声速飞行时,扰动能向前传播;跨声速时,弹头前方产生正激波,并随着马赫数上升而发展为斜激波;超声速时,激波逐渐附体,扰动只能向后传播。图中在舵面后缘、弹身靠近圆柱部的折转处和弹尾处存在膨胀波,速度存在突增情形。

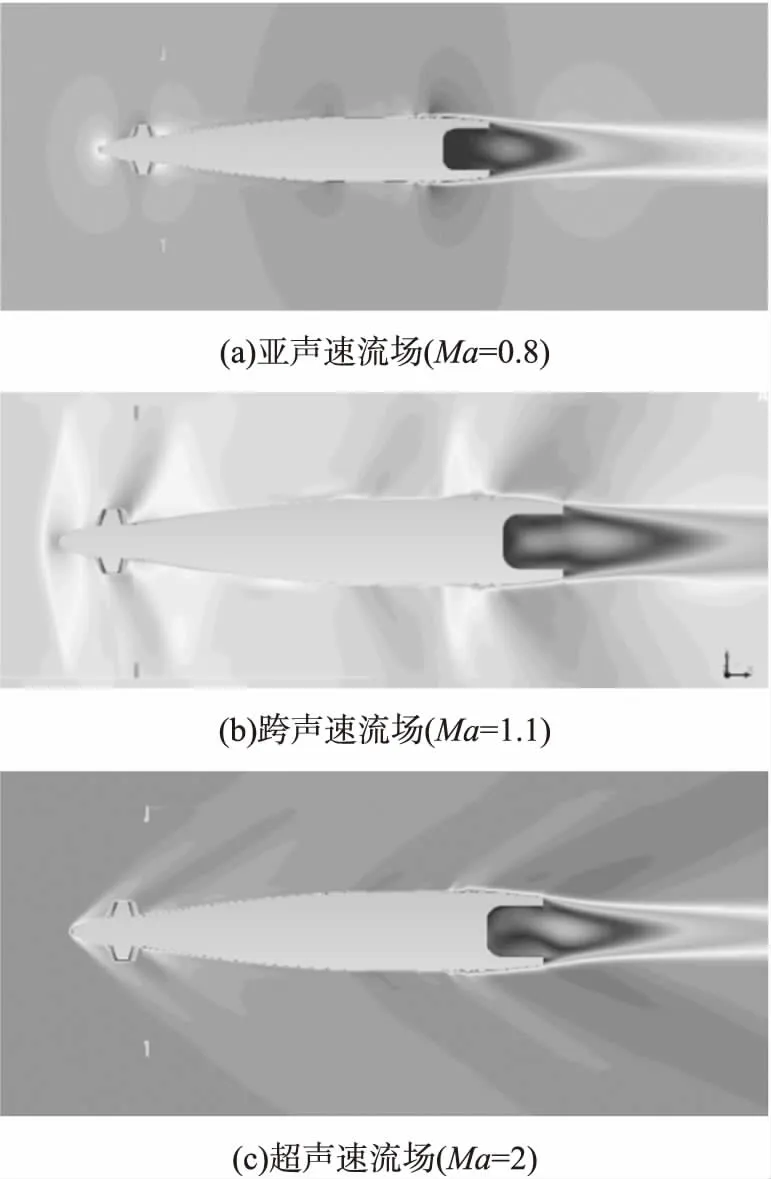
图5 不同马赫数,α=0°时的流场速度云图

2.2 横向流场

图6为不同工况下头部某一固定截面的压力云图,其中图6(a)～6(c)为定常计算的工况1,图6(d)～6(e)为非定常计算的工况2,图6(f)为非定常计算的工况3。由图6可以看出,在定常计算中舵面迎风面受到的压力明显高于背风面,在马赫数较小的情况下,扰动传播在舵面之间存在相互干扰,在同为迎风面的第三象限,压力明显高于其他象限;同理,在同为背风面的第二象限,压力最低。而在马赫数较高时,这种干扰几乎可以忽略,由舵偏产生的压差影响局限在舵面附近,不对其他舵片产生影响。

对比图6(a)～6(c)与图6(d)～6(e)可知,在非定常计算中,当组件反旋时舵面的压力分布向四周有扩散趋势,原本压力梯度在舵面与激波之间变化较大,而反旋时压力梯度较为平均。当具有一定攻角时,下舵面附近的压力比上舵面附近的压力高,下差动舵提供的导转力矩更大。图6(f)为弹丸进动到半个周期时的压力云图,此时同向舵仍为向上,但是弹轴指向下方,攻角提供的升力效果大,总体升力仍然指向下方,上方的差动舵处于迎风区,提供的导转力矩更大。

图6 不同工况下舵面附近的压力云图

3 计算结果及气动特性分析

3.1 定常工况下的气动特性分析

本节的定常工况结果可以总结该弹在不同马赫数和攻角下的气动特性,并为非定常工况结果提供对比。

3.1.1 阻力系数

图7给出阻力系数在不同攻角下的结果,由于计算的马赫数点较多,故图中仅给出4个马赫数数据点下阻力系数随攻角的变化。由图可见,随着攻角的增大,修正弹的阻力系数与普通弹丸规律相似,基本也和攻角呈抛物线关系,无攻角时阻力系数最小。阻力系数与攻角的关系式为

CD=CD1+CD2α2

(1)

式中:CD为阻力系数,CD1为阻力系数线性项,CD2为阻力系数非线性项。由此可得出如表1所示的非线性系数,表中,R2为线性回归中的判定系数,其值越接近1说明符合度越高。

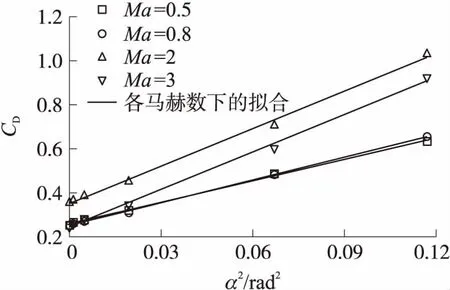
图7 阻力系数随攻角平方的变化

由图7和表1可见,采用传统阻力系数攻角模型对修正弹进行气动力参数的拟合效果良好,无论线性阻力项还是非线性阻力项,该固定鸭舵修正弹与普通弹丸的阻力系数规律基本一致;零升阻力系数在Ma=1.1左右达到最大;阻力系数的非线性项除了在跨声速略有波动外基本随马赫数增大而增大。

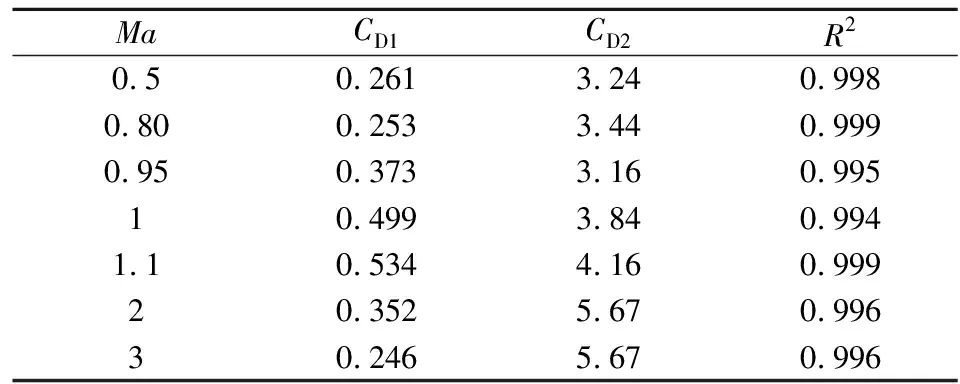
表1 阻力系数的线性项和非线性项

3.1.2 升力系数

图8为不同马赫数下该弹的升力系数随攻角的变化曲线。由图可见,升力系数在超声速区域与攻角呈较好的线性关系,而在亚、跨声速区间与攻角存在一定的非线性。

由于该弹在0°攻角时也产生升力和俯仰力矩,与普通弹丸存在区别，故假设升力系数的表达式为

CL=CL0+CL1α+CL2α3

(2)

式中:CL为升力系数,CL0为0°攻角时由俯仰舵产生的升力系数,CL1为升力系数线性项,CL2为升力系数非线性项。拟合结果如图8所示,得出的各项升力系数如表2所示。

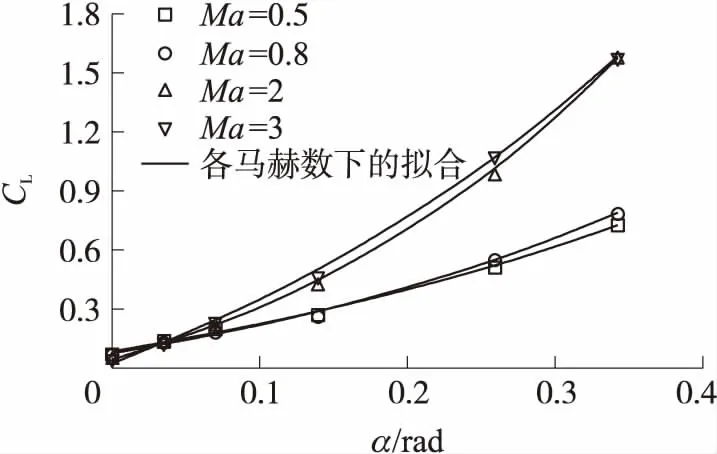
图8 升力系数随攻角的变化

表2 升力系数的线性项和非线性项

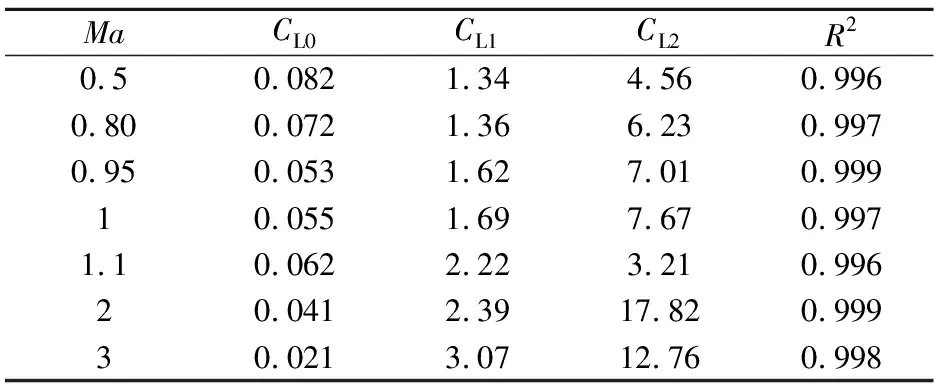
MaCL0CL1CL2R20.50.0821.344.560.9960.800.0721.366.230.9970.950.0531.627.010.99910.0551.697.670.9971.10.0622.223.210.99620.0412.3917.820.99930.0213.0712.760.998

由表2结果可见,该类固定鸭舵修正弹的升力系数线性项和非线性项基本随着马赫数增大而增大;由俯仰舵产生的升力系数增量在跨声速Ma=1.1左右达到最大。

3.1.3 俯仰力矩系数

图9为不同马赫数下俯仰力矩系数随攻角的变化关系。在小攻角下俯仰力矩系数与攻角近似呈线性关系,并且在0°攻角下也存在俯仰力矩;在大攻角下可以参考升力系数表达式,同样考虑俯仰力矩系数的非线性,有表达式:

CMz=CMz0+CMz1α+CMz2α3

(3)

式中:CMz为俯仰力矩系数,CMz0为0°攻角下由俯仰舵产生的力矩系数,CMz1为俯仰力矩系数线性项,CMz2为俯仰力矩系数非线性项,得出俯仰力矩的各项系数如表3所示,拟合结果如图9所示。

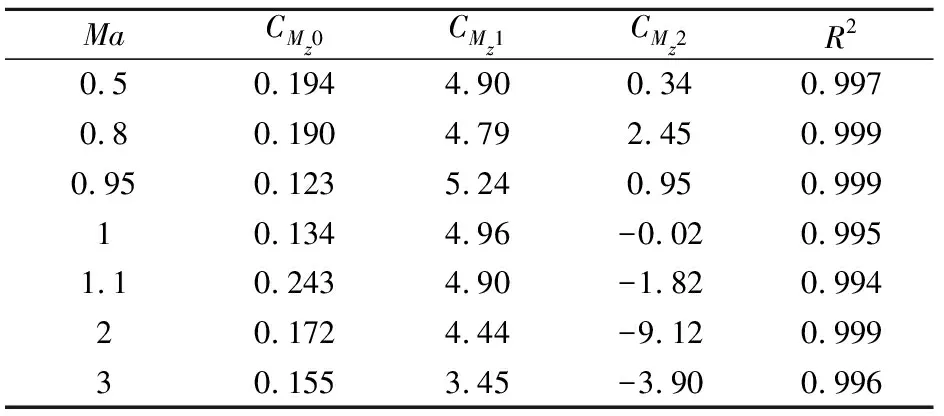
表3 俯仰力矩系数的线性项和非线性项

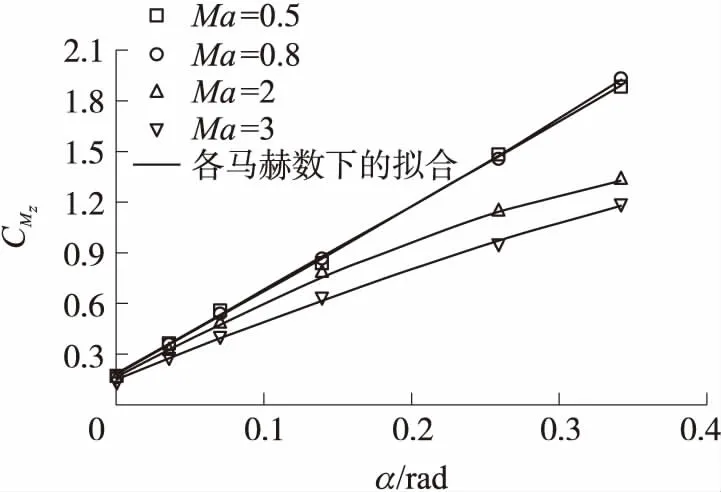
图9 俯仰力矩系数随攻角的变化

由表3结果可见,与一般旋转稳定弹相比,该弹的俯仰力矩系数非线性项CMz2的符号变化有所差异。该弹的CMz2在亚声速区域为正值,在超声速区域为负值,在跨声速区域由高马赫数到低马赫数呈由负到正的转变。

3.1.4 舵面导转力矩系数

鸭舵组件自由滚转时会产生滚转阻尼力矩,故在计算时将舵片方位固定,从而提取出较为准确的舵面导转力矩系数CMx。

图10为不同马赫数下导转力矩系数CMx随攻角的变化关系。

在Ma=1.1及以上和Ma=0.8及以下时,导转力矩系数随攻角的变化较小;在Ma=0.95和Ma=1时,由于鸭舵局部表面产生激波,其随攻角的变化较大;并且当Ma=0.95时,导转力矩系数先减后增,马赫数为1时,导转力矩系数先增后减再增。当攻角在0°～8°范围内时,导转力矩系数都随着马赫数变化而剧烈变化,且在攻角为8°时最为明显。

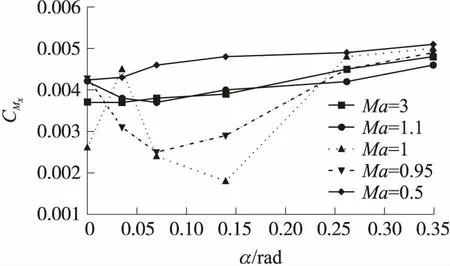
图10 导转力矩系数随攻角的变化

综上所述,当弹丸处于跨声速时,其舵面导转力矩系数随攻角的变化较为剧烈,舵面气动冲击较为剧烈,激波变化情形复杂,难以形成统计规律,因此在施加控制时应当尽量避开跨声速区域。

3.2 非定常工况下的气动特性分析

3.2.1 弹身高旋对气动特性的影响

由于定常工况下无法模拟弹丸的角运动及其自旋,针对弹身高速自旋情形,重点研究弹身自旋以及头部组件具有一定滚转速率后的气动特性。

图11中曲线为工况1的阻力系数曲线,实点为工况2非定常计算结果。由图可知,在相同马赫数下,工况1和工况2的计算结果非常接近。在理论上,弹丸高旋会产生附面层畸变和附面层位移,相当于改变了弹丸的外形,但结果表明这种改变对于弹丸纵向气动力特性的影响微弱,可忽略不计。

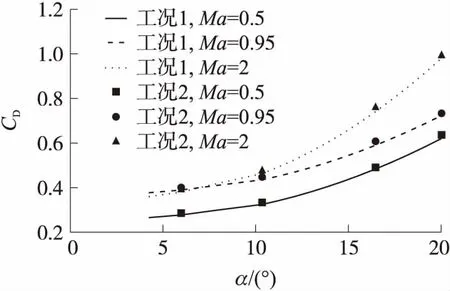
图11 工况2与工况1阻力系数的对比

另外,当头部以较慢的速度反旋时,组件的导转力矩减小,弹身阻尼力矩系数与头部组件有控静止时相比数值几乎不变。

3.2.2 进动角运动对气动特性的影响

模拟进动过程的步骤如下。

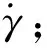
图12 进动模拟示意图

由于攻角面相对于速度系旋转,为方便讨论,这里的升力系数和俯仰力矩系数相对于速度系而言,即攻角面内的力和力矩在铅直面内的投影。图13给出了阻力系数、升力系数和俯仰力矩系数随鸭舵组件滚转角的变化。

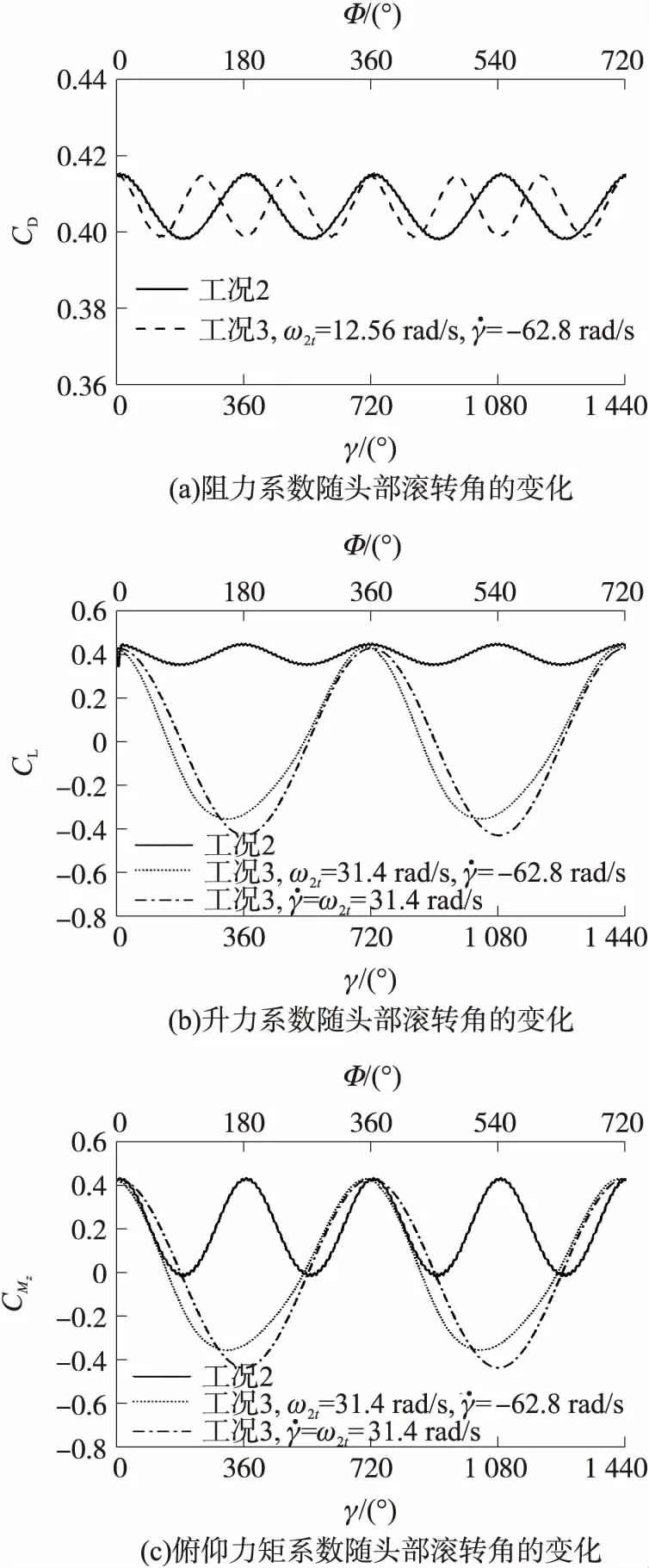
图13 进动频率较高时气动系数变化曲线

研究图13(a)中阻力系数的变化。在进动的1个周期内,组件在速度系内滚转2周,但相对于攻角面旋转3周;虽然鸭舵改变了总阻力系数,但是增量不到5%。

升力系数和俯仰力矩系数由攻角面位置和舵面位置共同决定,在本算例中两者的极小值出现在靠近半个进动周期之前的位置。如图13(b)、13(c),在弹运动到Φ=180°,γ=360°时,俯仰舵位置在水平方向并且向上偏,此时并不是升力系数最小的时刻;而当弹丸进动到1/4周期(Φ=90°)时,组件旋转了半周(γ=180°),俯仰舵向下,总体升力系数和翻转力矩为负。在1个周期内,升力系数最小值的绝对值略小于升力系数的最大值。由此可以得出,当使组件滚转周期与弹丸的进动周期成一定规律时,由舵面产生的升力改变弹道轨迹的效果微弱,升力大小主要由攻角幅值决定,而由舵面产生的翻转力矩占比较大,改变弹丸姿态的能力较强。

当ω2t=12.56 rad/s时,升力系数和俯仰力矩系数的变化如图14所示,弹丸进动1个周期,组件相对于速度系滚转了5周。可见由舵面产生的升力对全弹的升力贡献微弱,而由舵面产生的力矩占比很大。可以得到,当进动频率下降以后,俯仰舵产生的控制修正能力较大,能提供较大的翻转力矩。

图14 进动频率较低时气动系数变化曲线

以上2个算例考虑了弹丸的慢圆运动,模拟了固定鸭舵修正弹可能存在的2个飞行状态,得到了在1个进动周期内舵面滚转角对全弹升力系数、阻力系数、俯仰力矩系数的影响规律,但并未对存在动力平衡角的情形进行深入讨论。

4 结论

本文先对固定鸭舵修正弹进行了定常工况下的气动模拟,研究了其非线性气动力系数,之后分析了其具有自旋以及包含进动运动的气动特性,结论如下:

①与普通旋转弹类似,该弹的升力、阻力和翻转力矩也能较好地拟合出非线性气动系数,有利于在实际工程中分析该弹的稳定性;该弹的CMz2在亚声速区域为正值,超声速区域为负值,在跨声速区域由高马赫数到低马赫数由负转变为正。考虑静不稳定弹的陀螺稳定因子,CMz2为正不利于飞行稳定,可见为保证该弹的飞行稳定性需首先保证其亚声速范围内的飞行稳定性。

②该弹修正组件所受导转力矩系数在跨声速段随攻角的变化较为剧烈,即使在小攻角(α=5°)内也存在强非线性;在非跨声速段的变化则较为平缓,这对工程应用有重要参考价值。

③当进动频率和组件滚转周期符合一定规律时,该弹升力系数的非对称变化可能会对弹道产生微弱影响;而由舵面产生的翻转力矩改变弹丸姿态的能力较强。