电动涡旋压缩机转子的模态分析及试验研究

范子喆, 唐景春, 韩 凯

(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)

在电动汽车的空调系统中,电动压缩机是其核心部件。对电动涡旋压缩机的转子进行模态分析,提取其固有频率和相应的振型,可以为涡旋压缩机的工作转速设计提供依据,避免工作频率与固有频率重合造成的共振,降低动涡旋盘传动组件因振动产生的疲劳损伤和噪声,提高驾驶舒适度和压缩机使用寿命。

28 mL电动涡旋压缩机的结构示意图如图1所示,在其运转过程中,曲轴的振动通过轴承传递到壳体上,从而激发壳体及其他零部件的振动,当激振频率与系统的某阶固有频率接近时,振幅会急剧增大[1]。

固有频率和振型是转子结构设计中的重要动力学参数。文献[2]基于动力学理论讨论了涡旋压缩机曲轴的振动特点,建立了振动分析数学模型;文献[3]对六缸柴油机曲轴的模态进行了有限元分析;文献[4]对有限元分析中边界条件对模态试验的影响进行了研究;文献[5]对模态试验中测试点的选择方法进行了优化;文献[6]对涡旋分子泵的转子进行了模态分析和实验验证;文献[7]分析比较了曲轴和曲轴部件的固有频率和振型的差异;文献[8]对模态试验中力传感器的附加质量辨识及消除方法进行了研究;文献[9]开展了对模态试验中不同附加约束方式的对比试验。

图1 电动涡旋压缩机结构示意图

本文以振动分析理论为研究基础,利用ANSYS软件对28 mL电动涡旋压缩机曲轴转子进行模态分析[10],并利用激振器法对28 mL电动汽车空调涡旋压缩机的转子零件进行了模态测试。

1 模态分析理论

根据振动理论,一个具有N个自由度的线性结构系统中,运动的微分方程为:

(1)

进行如下简化假设:M、K是常量;不考虑阻尼影响,C=0;结构没有激励,F(t)=0;材料为线弹性材料,不包含非线性特性。

当不考虑阻尼和外界条件等影响因素时,方程(1)可简化为具有n个自由度的无阻尼自由振动微分方程:

(2)

(M+ω2M)x=0

(3)

其中,ω2为特征值,即固有频率的平方;x为特征向量,其物理意义表示振型。

无阻尼振动系统特征方程如下:

det(K-ω2M)=0

(4)

求解方程(3)的特征值问题,也就是求解方程(4)的根ωi(i=1,2,…,n),即可得到结构的固有频率和固有振型。

2 转子模态分析

2.1 实体模型及网格划分

28 mL电动涡旋压缩机的转子由曲轴转子、同步永磁体和固定于同步永磁体上用于二次平衡的平衡块3个部件组成。利用UG软件对其进行实体建模,如图2所示。

图2 转子几何模型

将实体模型导入ANSYS时,转子的同步永磁体和曲轴之间为过盈配合,过盈量取0.04 mm,网格划分后,转子的有限元模型如图3所示,含有38 810个节点和11 674个单元。

图3 转子有限元模型

2.2 基于有限元法的模态分析

ANSYS中模态提取方法主要有缺省方法(Block Lanczos)、子空间法(Subspace)、Power Dynamics法、缩减法(Reduced)、非对称法(Unsymmetric)、阻尼法(Damped)等。针对电动涡旋压缩机转子实体模型几何尺寸小的特点,采用缺

省方法计算模态,其材料属性定义见表1所列。

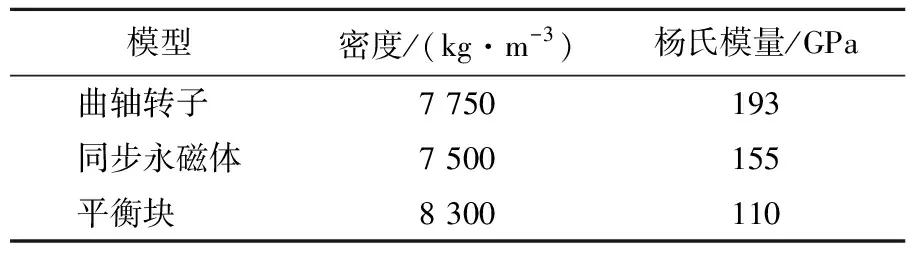
表1 各部件的材料属性

提取前4阶振动模态,振型如图4所示,对应的固有频率见表2所列。一阶振型表现为扭转振型,固有频率为87 Hz,可视为刚体模态;二阶和三阶振型表现为转子的两轴承中间段沿径向弯曲,固有频率相接近;四阶振型表现为二阶弯曲,振动的方向位于不同的平面内,曲柄销端部弯曲度较大。

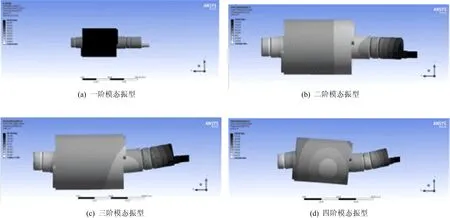
图4 模态仿真振型云图

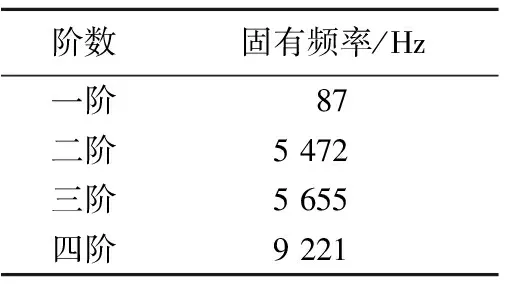
表2 模态仿真固有频率

3 转子模态试验

因为转子具有较强的磁场,采用激励锤方法产生的误差较大,所以激振系统选择更加稳定的激振器来施加激励频率。

转子模态试验装置如图5所示，由转子、激振器、加速度传感器、数据采集器、功率放大器以及计算机组成[12-13]。

试验分析采用LMS.Test.Lab17A软件,提取转子在无约束状态的固有频率,利用实测数据来验证有限元模型的准确性。

图5 转子模态试验装置

激振器给予转子激励频率使其产生振动,振动信号通过6个加速度传感器和数据线传到64通道的NVH测试分析系统,记录激励和响应的信号,经过数字信号处理,获得与响应激励自由度对应的频响函数,通过Modal Analysis中的Poly MAX提取出频响函数中的固有频率和振型。

试验获取的频响函数如图6所示,稳态图如图7所示,一阶模态的稳态图如图8所示，图6～图8中，振幅响应由加速度/力表征，加速度以g为基准，力的单位为N。

图6 频响函数

图7 稳态图

图8 一阶模态稳态图

求取固有频率和振型,转子的振型如图9所示。转子固有频率的试验结果与计算结果对比见表3所列。

表3数据表明,2种方法获取的固有频率值之间的最小误差为四阶的0.8%,最大误差为二阶的7.9%。

误差产生的原因如下:

(1) 对转子实体模型进行了简化,输入的材料属性与实际的材料属性存在一定的误差。

(2) 仿真算法基于线性理论,而实际转子由许多部件组成,存在非线性因素。

(3) 试验时转子利用胶水和磁性固定于激振器上,对试验结果有一定影响。

(4) 电动涡旋压缩机转子体积小、质量轻,6个加速度传感器的附加质量对模态试验产生了一定的误差影响。

图9 试验模态振型

对涡旋压缩机转子进行模态分析的主要目的是为了避免激励频率接近一阶模态固有频率而引起的共振,一阶临界转速为87 Hz(5 220 r/min),实际转速应偏离临界转速20%以上,因此压缩机转子的额定工作转速应低于4 176 r/min或者高于6 264 r/min。

试验测得的转子模态参数与仿真计算的结果基本吻合,表明了本文模态分析的有限元模型是较为准确的。

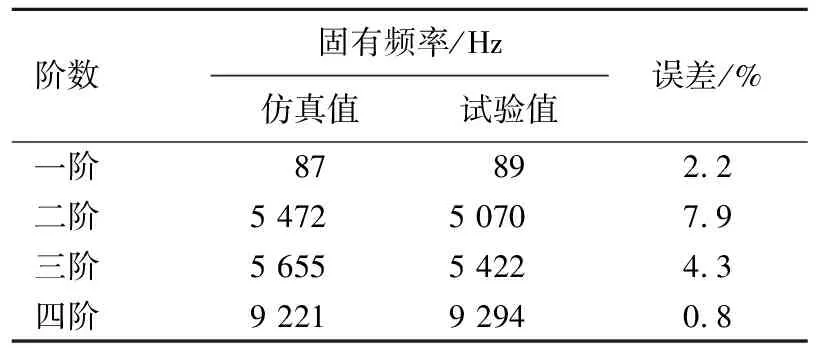
表3 计算模态与试验模态结果对比

4 结 论

(1) 本文建立了电动涡旋压缩机转子的有限元模型,通过网格划分与约束,得到了前4阶固有频率和相应的振型图,其中一阶固有频率为87 Hz。

(2) 用激振器法对压缩机转子进行了模态试验,并对仿真结果与试验结果产生误差的原因进行了分析。比较试验数据与计算模态结果可知,前4阶的固有频率最大误差为7.9%,小于10%,验证了压缩机转子模态分析有限元模型的准确性。

(3) 转子的模态分析为其曲轴的研发与优化设计提供了理论数据,根据仿真模态的固有频率,28 mL电动涡旋压缩机转子的额定工作转速应低于4 176 r/min。