有限热源下斯特林制冷机的χ函数优化

王寿海，吴锋，云慧敏，章超明

(武汉工程大学光电信息与能源工程学院，湖北 武汉 430205)

0 引言

当前，节能问题备受重视.斯特林制冷机因具有制冷范围广、效率高、体积紧凑等优势而受到业界的青睐.以有限时间热力学的方法进行优化分析，对提高能源利用率、保护生态环境降低污染意义重大.

在有限热源方面，陈林根、孙丰瑞、李俊等[1-7]研究了有限热源下具有热漏的双热源热机的优化配置，并论证了热机在有限时间内有限尺寸、有限热容以及热漏对最大功率、最大效率以及最优循环的重要性.叶兴梅、苏孙庆等[8-9]建立了有限热源下不可逆气体的ST热机模型，并得出了输出功率和效率两者之间的关系.吴锋[10]、马一太[11]、黄跃武[12]研究了变温热源对不可逆制冷机的影响，将制冷系数的面积比ε/A作为新的目标函数进行了优化分析，并对其火用输出率和火用效率的关系进行了探讨.在斯特林制冷机方面，Hachem H[13]，Luo E C[14]提出了斯特林的参数化理论和实验研究，并讨论了制冷机的制冷量、COP、损耗以及制冷温度，得到了制冷率取最大值时所对应的孔隙率.Ahmadi M H[15]研究了纳米尺度的大小对不可逆斯特林制冷机的影响，通过对两种不同的多目标进行优化，得出将MECOP最大化，可以得到ESI、ECOP的最大值和ecf的最小值.杨惠山[16]、田鑫泉[17]、严子浚[18]对斯特林制冷机的性能系数、制冷率、生态学以及回热性能进行了优化分析.

制冷率和性能系数是衡量制冷机工作效率的重要参数.当制冷率达到最大值时，性能系数的取值较小；而当性能系数取最大值时，制冷率则为0.为了能较好地解决制冷率和性能系数的平衡，严子浚于1984年在自然杂志中提出了χ准则，它是性能系数与制冷率的乘积.其后de Tomás C[19]、隆瑞[20]又将费曼棘轮-棘爪制冷机在最大性能系数、最大制冷率和χ准则优化下的性能进行了对比分析，得出在相同条件下χ准则下的制冷率和性能系数可同时达到最优值，相对于单一追求最大性能系数和最大制冷率而言，该准则下制冷机的整体性能更佳，更具优势和研究意义.本文中将该准则应用于不可逆斯特林制冷机中，建立含热阻、不可逆因子、热漏的不可逆模型，最终分析得出相关参数对χ*-ε和χ*-r*的影响.

1 斯特林制冷机的循环模型

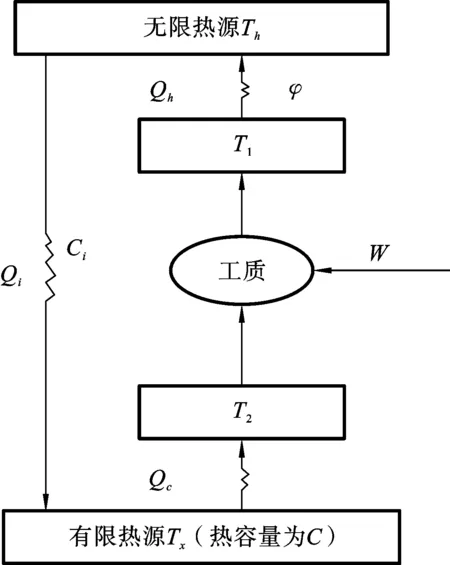
图1 斯特林制冷循环模型

假设将理想气体作为斯特林制冷机的工质，工质工作于高温热源(大气环境)温度为Th的无限热源，低温热源(制冷对象)为有限热源，设其热容量为C，由于热容量有限，设TL和TL1分别为制冷循环开始和结束时低温热源的温度，Tx为低温热源的瞬时温度，则TL1≤Tx≤TL.制冷机工质在等温压缩和等温膨胀时的温度分别为T1和T2.整个循环过程的模型如图1所示.

图1中，高、低温热源与工质之间的热量交换分别为Qh、Qc，不可逆因子为φ，高、低温热源之间发生的热漏为Qi，热漏所对应的换热系数为Ci，外界环境向制冷机内部的输入功为W.

制冷循环的换热过程满足牛顿线性传热规律，制冷机工质与高低温热源之间在经历等温压缩、膨胀过程中的换热量为：

dQ1=α(T1-Th)dt

(1)

dQ2=β(Tx-T2)dt

(2)

式中，α、β分别为高、低温热源和制冷机工质的传热.

低温热源的热容量是有限的，故而低温热源与工质的热量交换过程亦可表示为：

dQ2=-CdTx

(3)

对公式(3)进行积分可得：

Q2=CΔT=C(TL-TL1)

(4)

联立公式(3)、(4)可得：

β(Tx-T2)dt=-CdTx

(5)

(6)

制冷机工质为理想气体，故内可逆过程高、低温热源和工质的换热量分别为：

Q1=nRT1lnλ

(7)

Q2=nRT2lnλ

(8)

若不考虑热漏，仅考虑循环的内不可逆性，一般内不可逆性主要表现在高温热源与制冷机工质的换热过程中，可得ST制冷机工质和高、低温热源的换热量分别为：

(9)

(10)

2 目标函数

分别对公式(1)进行从等温压缩前的状态1到等温压缩后的状态2的积分，对公式(5)进行从等温膨胀压缩前的状态3到等温膨胀后的状态4的积分，可得到工质在经历等温压缩和等温膨胀的时间分别为：

(11)

(12)

假设制冷机工质定容过程的时间t3、t4与等温过程成正比关系，则整个制冷循环所经历的时间为：

(13)

式中k为比例常数.

热漏损失：热源之间的热量损失如下：

Qi=Ciτ(Th-Tx)=τqi

(14)

式中，Ci——高低温热源之间的换热系数；τ——制冷机的循环周期；qi——热漏率.

考虑内不可逆性、热漏损失等不可逆因素，分别联立公式(6)、(9)、(12)以及(10)、(12)可得实际不可逆ST制冷机工质和高、低温热源之间交换的热量为：

Qh=φQ1-Qi

(15)

Qc=Q2-Qi

(16)

由此可得制冷率和性能系数分别为：

(17)

(18)

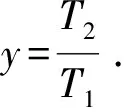
(19)

将公式(19)分别代入到公式(17)～(18)中，可得到最佳压缩温度下所对应的最佳制冷率以及最佳性能系数为：

(20)

(21)

同时将制冷率和性能系数综合考虑，引入χ准则[19]：

(22)

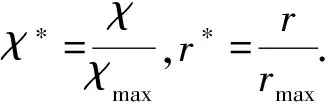
3 数值计算

本文中χ准则作为目标函数，分析各种不同的参数对χ函数整体的影响.取热容量C=1 000，Th=300，TL=77，ΔT=TL1-TL.

图2 热漏和不可逆因子对χ*-ε的影响

由图2可得，χ*-ε的曲线关系呈柳叶形分布.图2(a)中热漏率qi分别取20 w/s、30 w/s、50 w/s时，函数χ*在性能系数ε=0.14时取得极大值，热漏只影响函数χ*极大值的取值，并不影响极大值点(ε)的值，且热漏率越大，函数的极大值越小.图2(b)中不可逆因子φ分别取1.2、1.3、1.5，函数χ*随着不可逆因子的增大而逐渐减小.

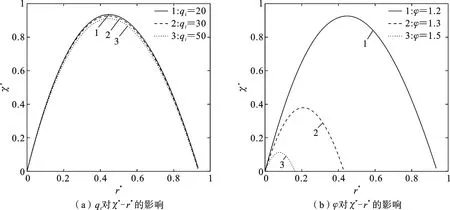
图3 热漏和不可逆因子对χ*-r*关系的影响

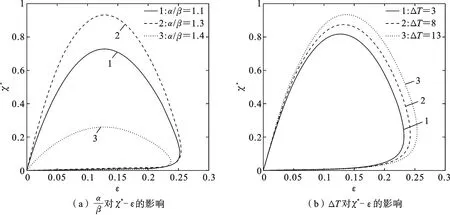
图和ΔT对χ*-ε关系的影响

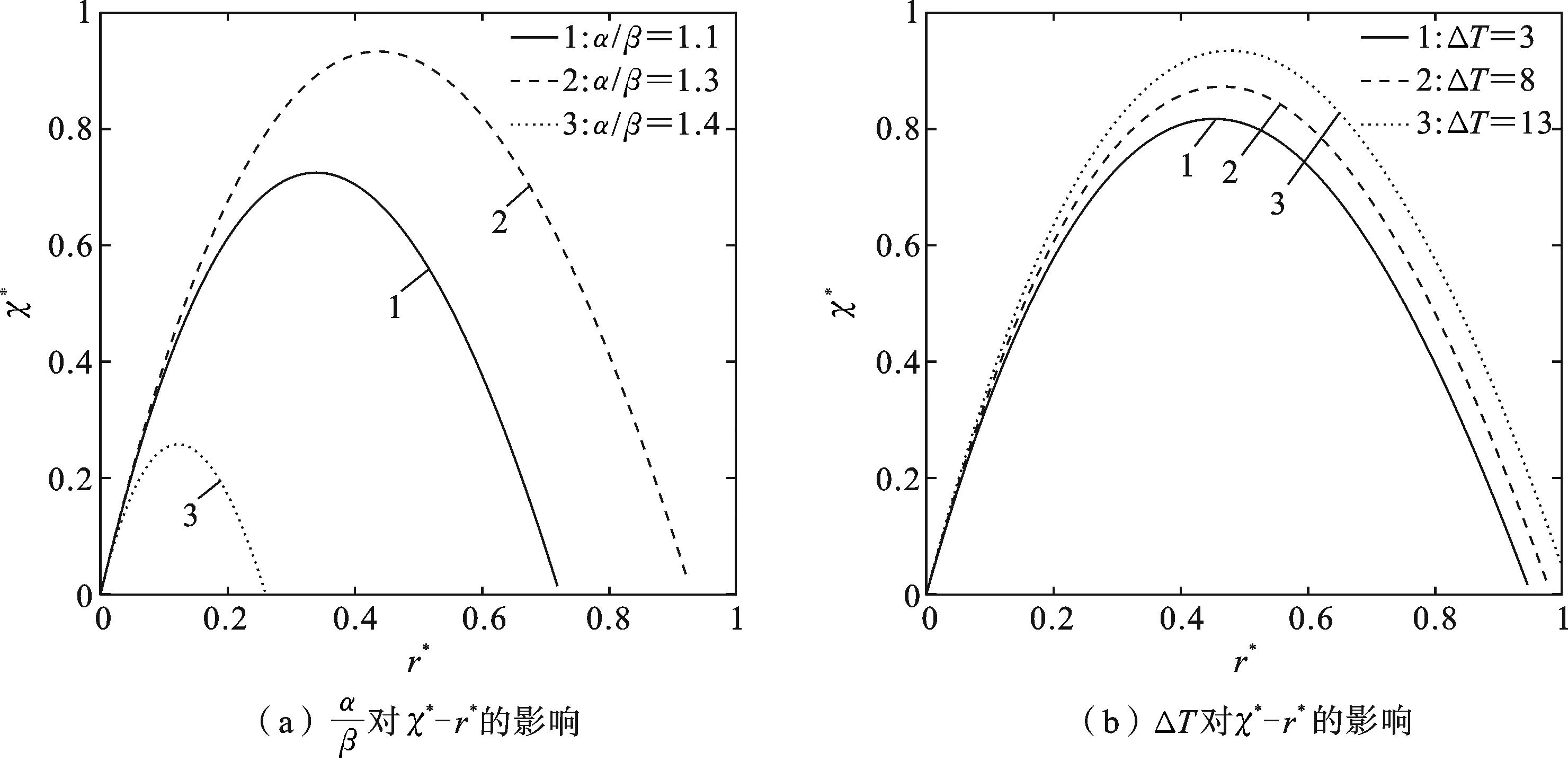
图和ΔT对χ*-r*关系的影响

4 总结

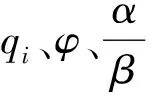
综上所述，减小热漏和不可逆因子，选择合适的传热系数之比以及尽可能提高低温热源的温度变化量，对提高斯特林制冷机的性能尤为重要.