基于零空间行为法的自主水下机器人避障策略

庞师坤， 梁晓锋， 李英辉， 易 宏

(上海交通大学 海洋智能装备与系统教育部重点实验室；海洋工程国家重点实验室，上海 200240)

自主水下机器人(AUV)是具有智能行为的高级水下机器人，具有活动范围广、机动灵活、隐蔽性好等特点，能够适用于复杂的海底环境.为了在不可预知的海底环境中安全完成既定任务，AUV要能够利用自身携带的传感探测设备(声呐、摄像头等)并结合相应的算法进行实时避障.人工势场法[1-4]、动态窗口法[5-7]、A*及其改进算法[8-13]、基于行为法[14-18]等，是目前应用较多的避障方法.

基于行为法广泛应用于诸如移动机器人、无人艇、无人机等的无障碍路径规划领域.无障碍路径规划采用自底向上的系统构建方法，基于行为法将任务目标分解为一系列相互作用的基本子行为，如感知、探测、避障、规划，构成并行控制回路，通过协调配合后作用于执行机构，产生相应的目标任务动作.单个子行为仅需要完成某项简单任务，能够对环境产生快速响应，并且可以灵活地扩展整个系统的能力[19].行为选择机制主要有行为抑制法、加权平均法和模糊逻辑法[20].其中模糊逻辑法可以实时地调整任务权值，从而优化任务完成的质量，因此在实际应用领域很受欢迎.文献[21]提出的零空间行为(NSB)法即为模糊逻辑法的一种.与其他基于行为的方法相比，NSB法在保持首要任务完全完成的前提下，可以充分利用零空间完成其他次要任务，具有实时性强、各子任务间零冲突的优点.

本文采用NSB法，针对AUV在复杂海底环境中对静态和动态障碍物的规避进行研究.在按需对整体任务进行分解的基础上，建立不同优先级的子任务函数，并对不同障碍物的避障策略进行分析.

1 NSB法

NSB法首先将整体任务，即驶向目标点，分解成多个各自独立控制目标的子任务，并分别列出各子任务函数，每个子任务函数都能完成对应的控制目标；然后将子任务分成不同的优先级，将由低优先级的任务向量向高优先级任务向量的零空间投影得到任务的整体综合输出函数传递给底层的执行机构以控制AUV的动作.设：η=[xyψ]T为AUV惯性坐标系下的位置和艏向角；ν=[uvr]T为AUV随体坐标系下的速度和转艏角速度(u为纵向速度，v为横向速度，r为转艏角速度)；σ为控制目标的任务变量，其函数模型为

σ=f(η)

(1)

将σ对η求导可得

(2)

式中：J(η)为η的输出雅可比矩阵.

速度矩阵的最小二乘解为

(3)

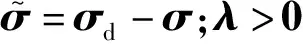
用i表示任务的优先级(i=1时，任务优先级最高)，第i个任务的速度输出可表示为

(4)

第i个任务的向较高一级任务零空间的投影为可表示为

(5)

式中：I为单位矩阵.

由低等级的任务向较高一级的任务空间投影，可得出整体控制目标的速度输出为

(6)

当有3个不同等级任务时，综合任务的速度输出可表示为

vd=v1+N1(v2+N2v3)

(7)

以两个任务为例，其综合输出速度的几何模型如图1所示.v2首先向v1的零空间投影，进而得到vd=v1+N1v2，vd为任务速度v1和任务速度v2的NSB输出.

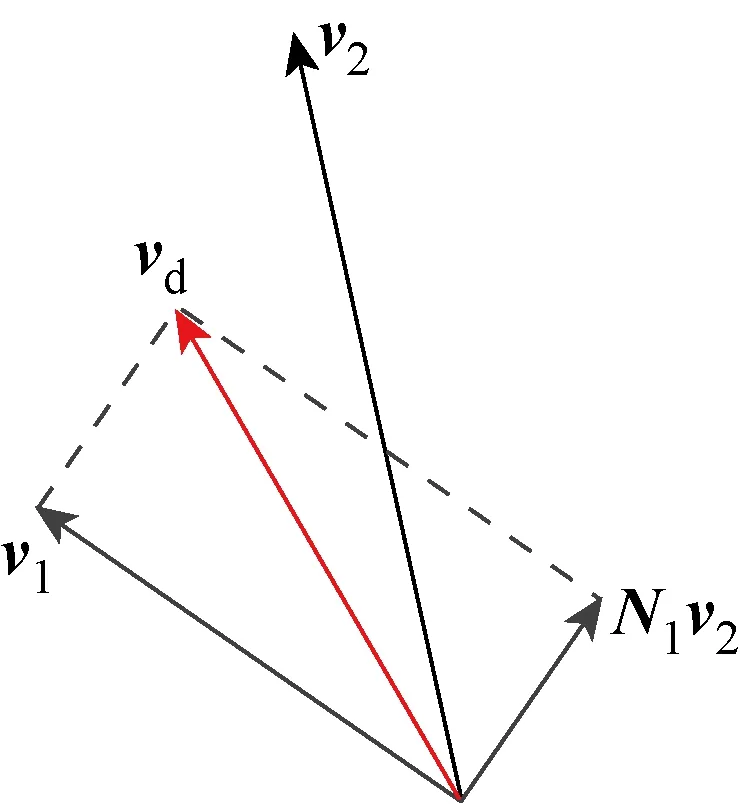
图1 两任务时综合输出速度的几何模型

2 避障策略

本文主要针对AUV对平面内不同类型障碍物的避障策略进行分析讨论.为便于分析模拟，根据实际情况和AUV绕过障碍物的方向，假设：

(1)障碍物无法与AUV进行通信且不会对AUV进行主动规避.

(2)AUV可以探测到相对于动静态障碍物的运动速度和方位角，选择逆时针或者顺时针方向绕过障碍.

(3)AUV可以探测到当前时刻动态障碍物的速度，但是无法预知其下一时刻速度，因此假设动态障碍物的运动速度是固定的.

根据假设(1)，当AUV利用自身携带的传感器(声呐、摄像头等)探测到障碍物时，需根据障碍物类型进行主动规避.单个静态障碍物类型相对简单，文中不再赘述.针对动态障碍物，可分为正面障碍物(见图2)和侧面障碍物(见图3)两大类.对于正面障碍物，AUV可以选择顺时针或逆时针方向进行规避(本文设为逆时针规避)；对于侧面障碍物，AUV需要判断自身与障碍物的相对运动方向和方位，选择合理的转艏方向，从而顺利规避障碍物.

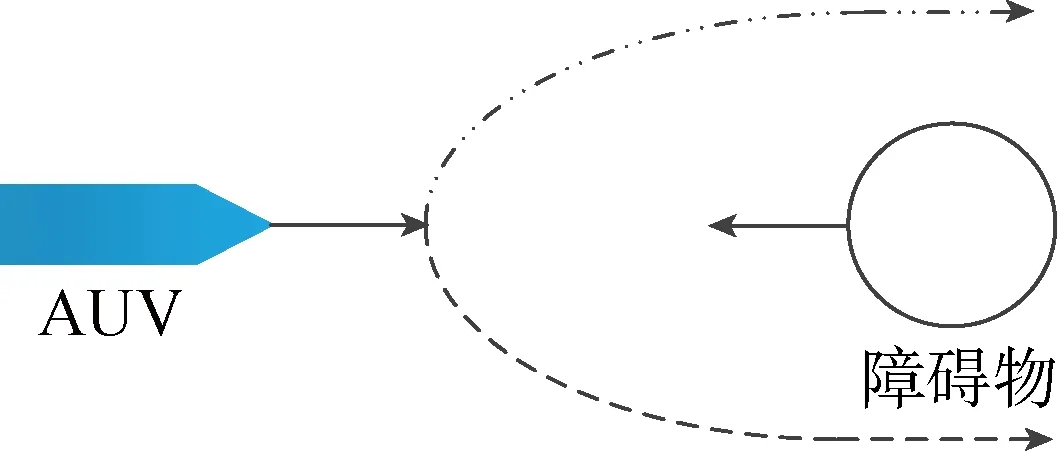
图2 正面障碍物

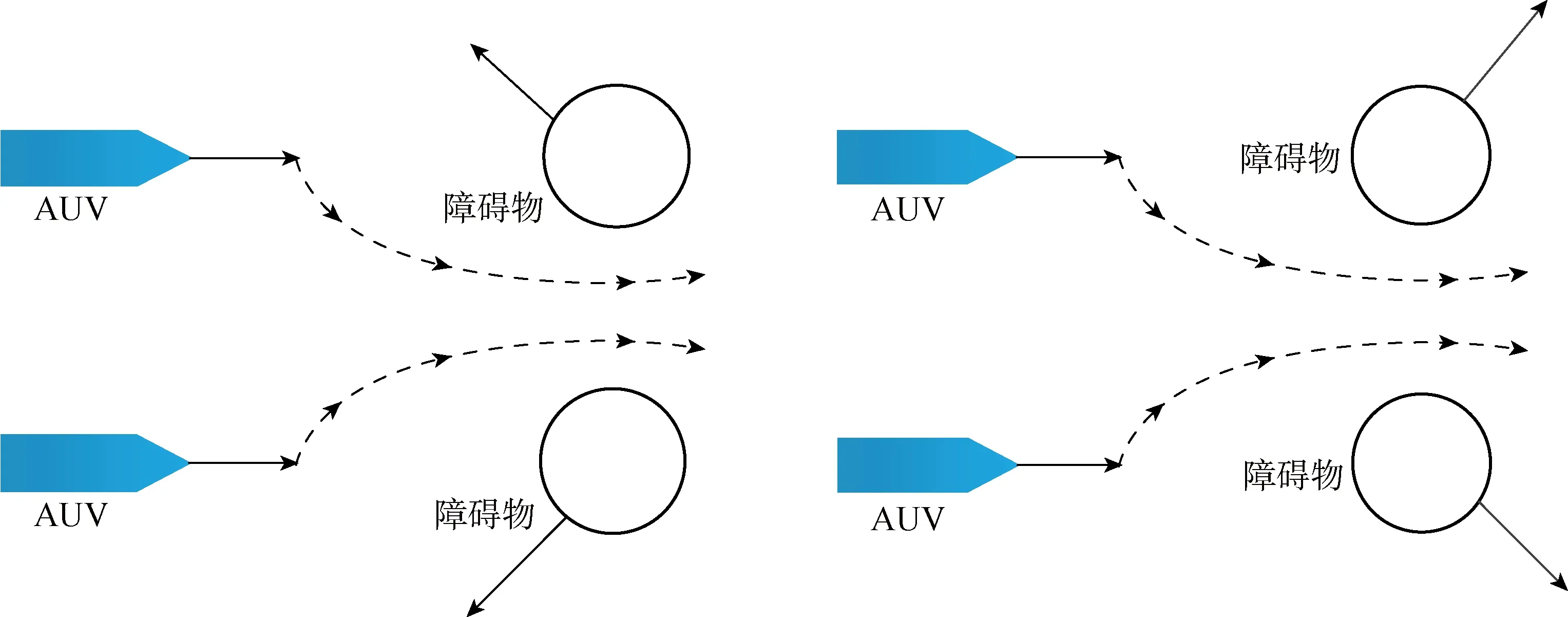
图3 侧面障碍物

根据假设(2)，首先将障碍物的速度转换到AUV随体坐标系上:

(8)

式中：上标b和n分别表示随体坐标系和惯性坐标系；R(θ)为转换矩阵；θ为转换角.

AUV在随体坐标系下相对障碍物运动方向为

(9)

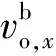
由于β(见图4，图中vo和vv分别为障碍物和AUV的速度)的取值范围为-180°<β<180°，而常规的四象限定义0°<β<360°，所以当β<0°时，β需在原来的基础上加360°，从而满足要求.AUV根据β所在的象限，选择绕过障碍物的方向，当β在第 I 和第 II 象限时，选择顺时针方向，当β在第 III 和第 IV 象限时，选择逆时针方向.在此情形下，AUV从障碍物后面绕过且两者方向没有交叉，因此路径是安全的.

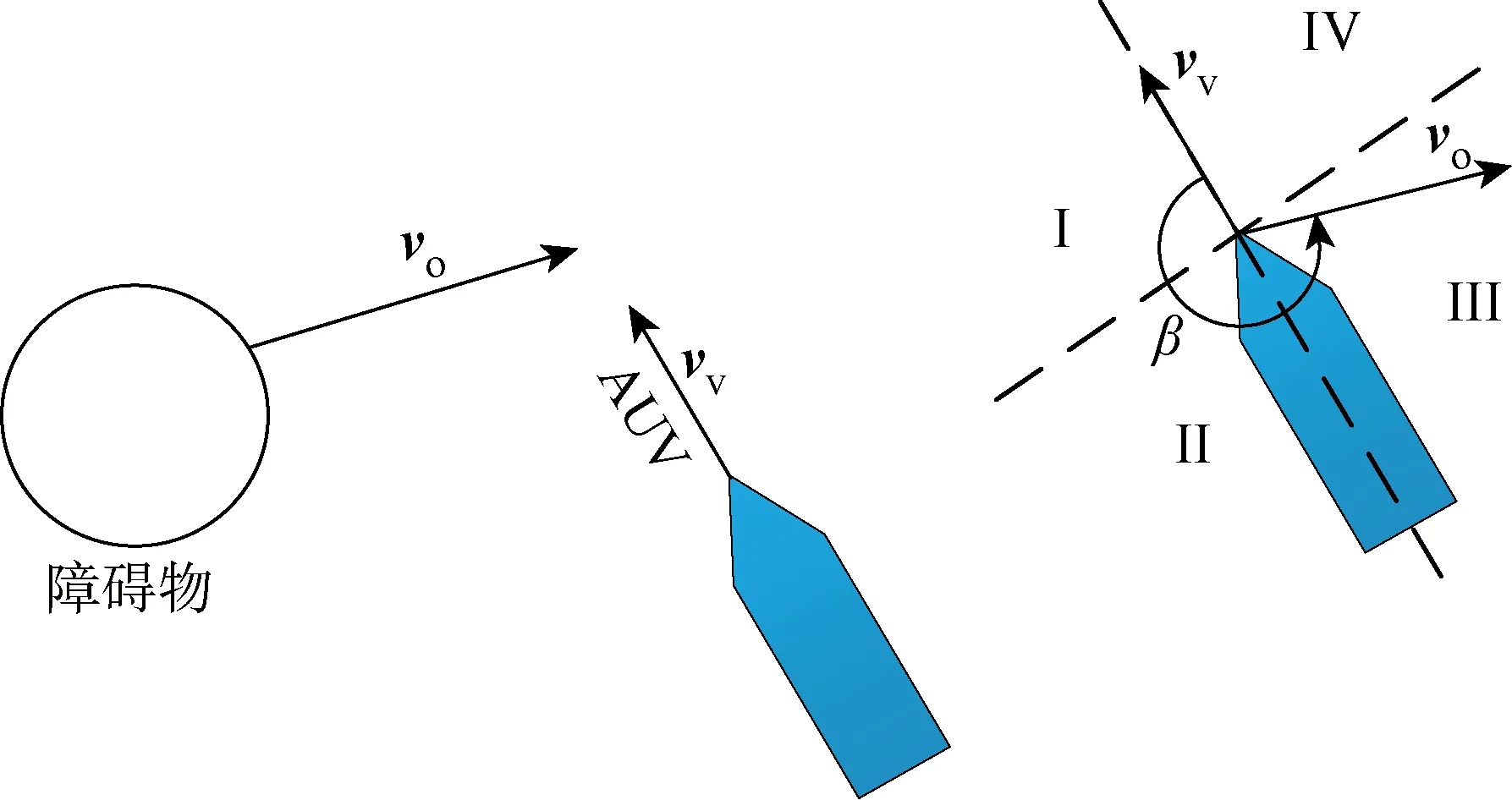
图4 β角象限示意图

文中设定当AUV运动方向相对于障碍物的运动方向角度的绝对值小于20° 时为正面障碍物，此时|β-180°|≤20°.

2.1 障碍物探测

AUV和障碍物的路径V(t)和O(t)分别表示为

(10)

(11)

式中：θvt为AUV到目标点的方向角；θo为移动障碍物的方向角；t为时间变量；pv,x、pv,y和po,x、po,y分别为当前时刻AUV和障碍物的位置，两者之间的距离为

(12)

首先当AUV探测到障碍物时，启动避障算法.AUV根据当前时刻自身和障碍物的速率以及相对方向角等信息，计算下一时刻两者的相对位置.根据假设(3)，当f(t)进入到障碍物的安全范围内时，AUV开启避障子任务.根据迭代信息和NSB算法，AUV判断是否已经安全绕过障碍物.如图5所示，当AUV在位置a时，探测到障碍物，同时估算路径并启动避障算法，此后则一直进行探测和位置的迭代更新；在位置b时，AUV根据实时更新的障碍物相对位置和方位角，再次进行路径估算，判断路径是否安全；在位置c时，确认路径安全，避障算法停止，AUV驶向设定目标点.

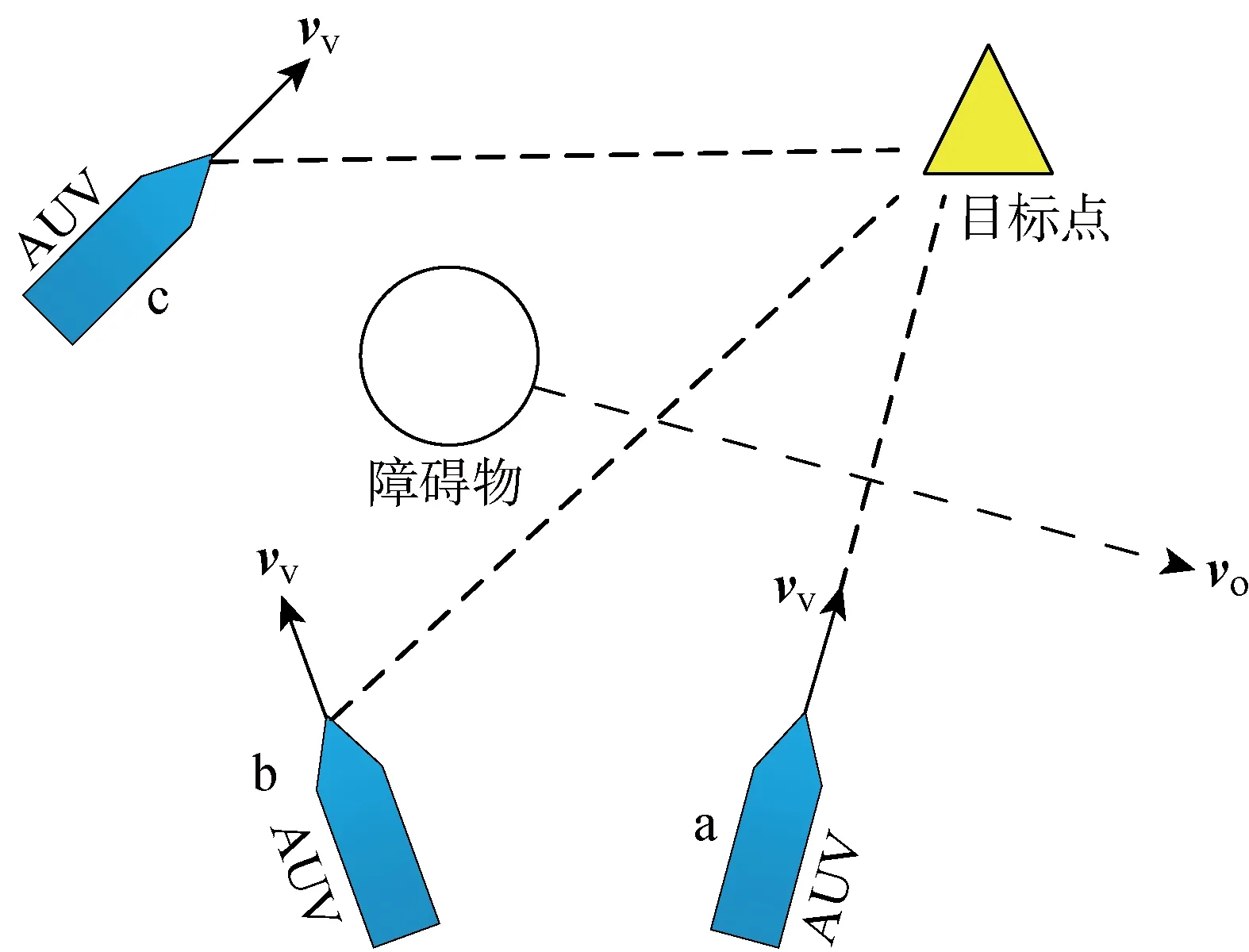
图5 AUV避障过程

2.2 任务分解

为了使基于NSB法的避障策略能够处理静态和动态障碍物，并根据前文所述的避障策略选择绕过障碍物的方向，按照不同优先级将避障任务分解为任务1(避障)、任务2(绕过障碍物)、任务3(驶向目标点)3个子任务，同时根据AUV与障碍物之间的相对距离将障碍物周围分为安全区、常规避障区和紧急避障区3个区域(见图6).在安全区内，认为障碍物对AUV无威胁，AUV正常驶向目标点，即为任务3；在常规避障区内，AUV探测到障碍物，启动任务2，关闭任务1、3，以便AUV选择绕过障碍物的方向和虚拟切点位置；在紧急避障区内未绕过障碍物前，AUV启动任务1、2，关闭任务3，确保AUV以最佳路径顺利绕过障碍物；确认绕过障碍物后，在避障区内任务1、3同时启动，关闭任务2；驶出避障区后，关闭任务1、2，开启任务3，AUV重新规划路线，选择最短路径驶向目标点.

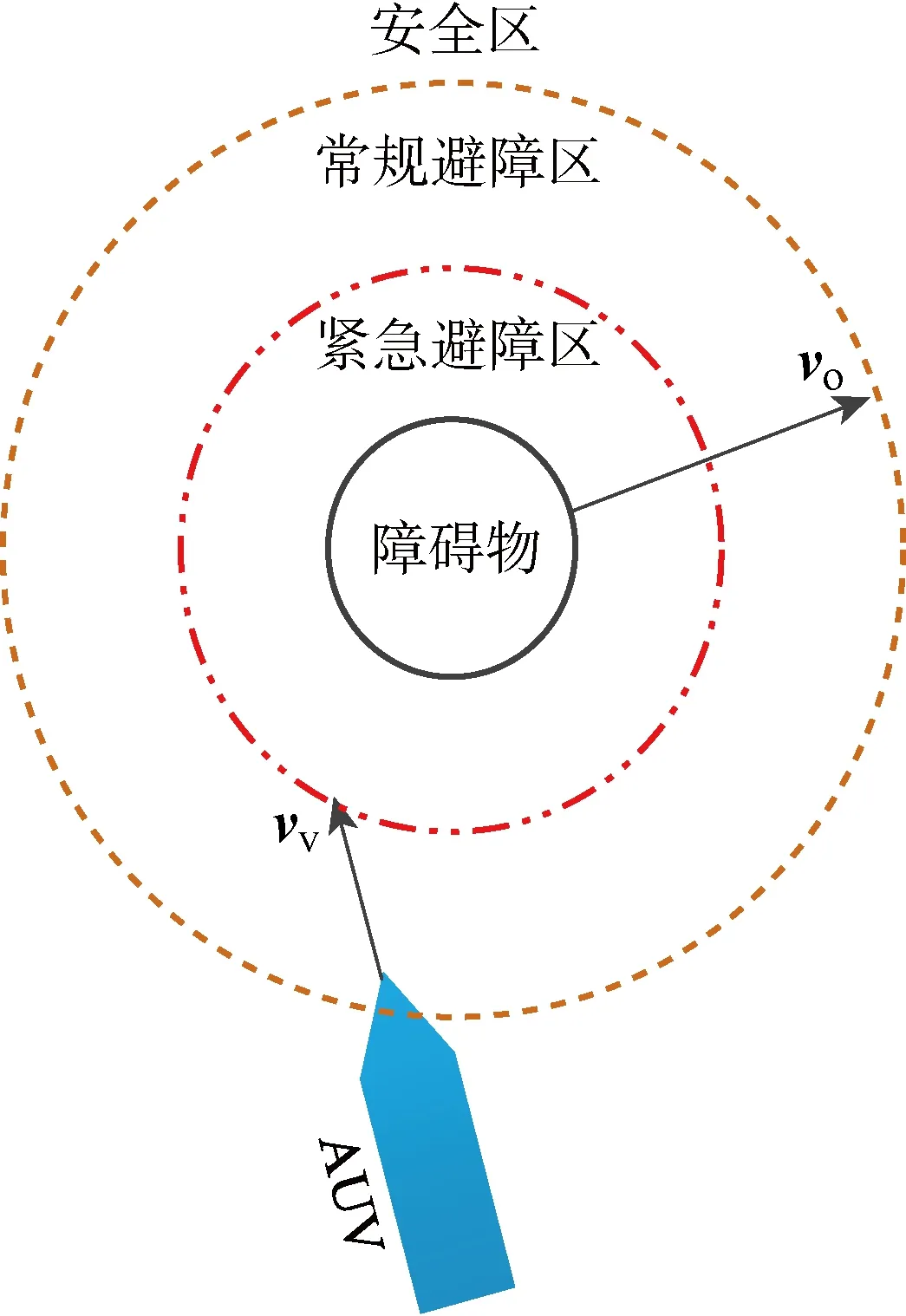
图6 不同避障区

任务1避障.在多控制目标任务中，避障任务作为最高优先级，任务变量σ1表示AUV的位置Pv到障碍物中心Po的距离：

(13)

σ1,d为障碍物的安全阈值(安全距离)：

σ1,d=d

(14)

对应的雅可比矩阵为

(15)

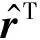
任务1的输出速度为

(16)

式中：λ1为任务1的增益矩阵.其零空间向量为

(17)

任务2绕过障碍物.作为第2优先级的控制目标任务2，引导AUV按照顺时针或者逆时针方向绕过障碍物，其任务变量为

(18)

(19)

式中：to为障碍物上的虚拟切点.

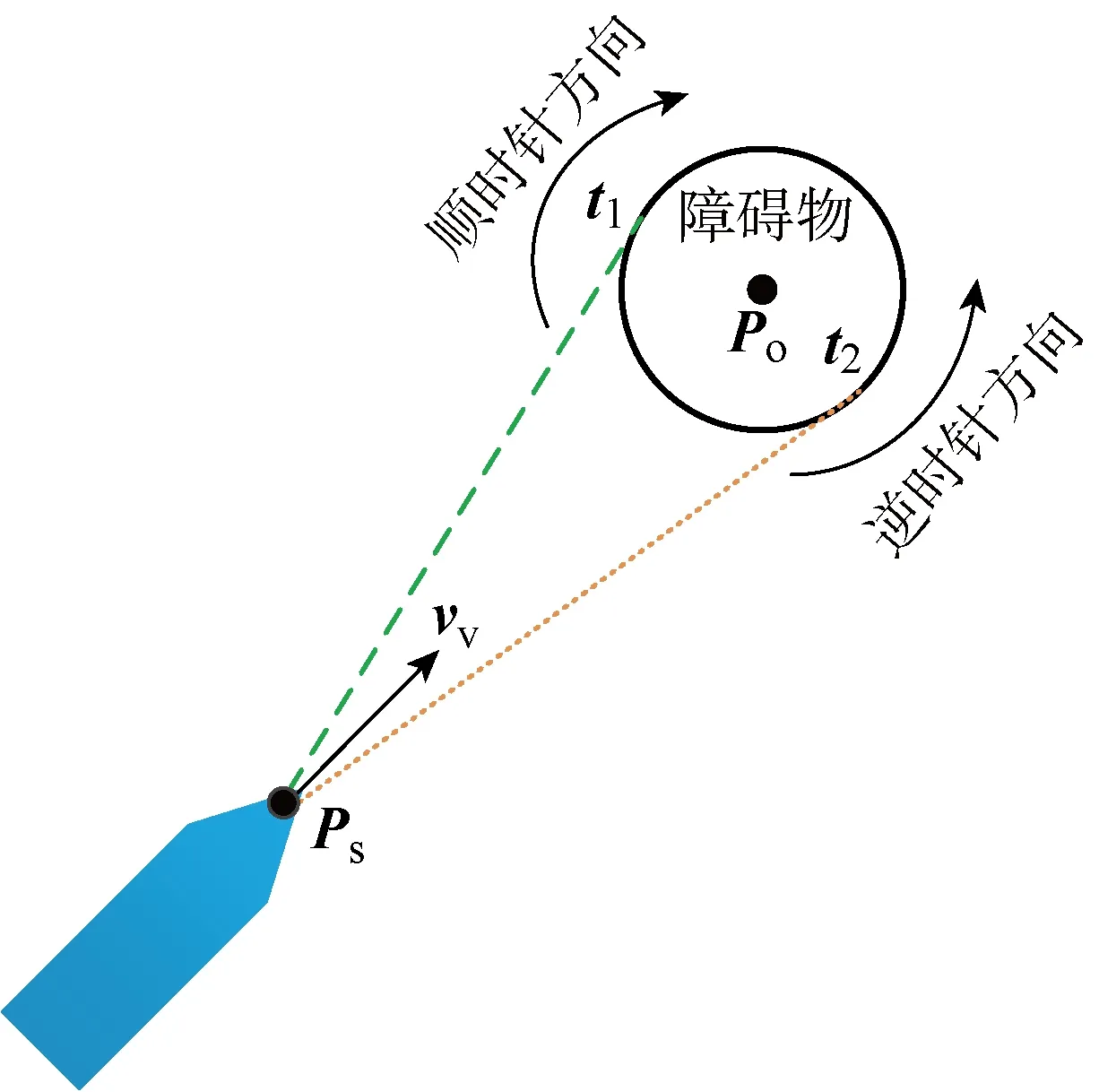
图7 虚拟切点示意图

首先定义起始点Ps分别到障碍物中心点Po和切点t1(见图7)的向量Pso和Pst1：

Pso=Po-Ps

(20)

Pst1=t1-Ps

(21)

其长度分别为

(22)

(23)

式中：ro为障碍物半径.

然后确定Pst1与xOy平面的夹角θt1：

式中：θt1,1为Pso和Pst1之间的夹角；θt1,2为Pso与xOy平面的夹角.

设二维转换矩阵R(θ)为

(27)

则切点t1为

(28)

式中：dt为当前时刻AUV距离障碍物的距离.

同理，当AUV逆时针绕过障碍物时，

θt2=θt2,2-θt2,1

(29)

切点t2为

(30)

任务2的变量为一条直线，其雅可比矩阵为

提高高速公路工程建设质量具有重要意义，对此公路建设管理工作必须在创新驱动下积极开展创新活动，从管理思路、管理方法、技术标准等多个环节开展创新活动，积极引入新技术、新方法，从管理制度开始调整，重视科技创新工作，多种方法共同使用，以提高高速公路建设管理水平。

J2=I

(31)

输出速度为

v2=λ2(to-Pv)

(32)

式中：λ2为任务2的增益矩阵.

那么零空间N2=0，任何低级任务的输出速度投影到该任务空间，投影都为0.考虑到任务2和任务3不可能同时激活，因此该零空间亦不会使用.

任务3驶向目标点.在本文中最低优先级为驶向目标点的控制目标任务3，在AUV避障任务完成前后，确保AUV沿最短路径到达目标点.考虑到AUV沿直线到达目标，其任务变量为

同任务2类比，其雅可比矩阵、输出速度和零空间分别为

式中：Pt为目标点位置；λ3为任务3的增益矩阵.

根据式(6)，AUV的综合任务速度输出为

vd=v1+N1v2+N1N2v3

(38)

为了保证避障任务的顺利完成，本文设计了适用于NSB法的任务管理器(见图8和9).任务管理器根据AUV探测到的障碍物和避障算法，决定何时激活和抑制对应的任务.特别需要注意的是，当任务1未激活时，任务2、3无需向该任务零空间进行投影.

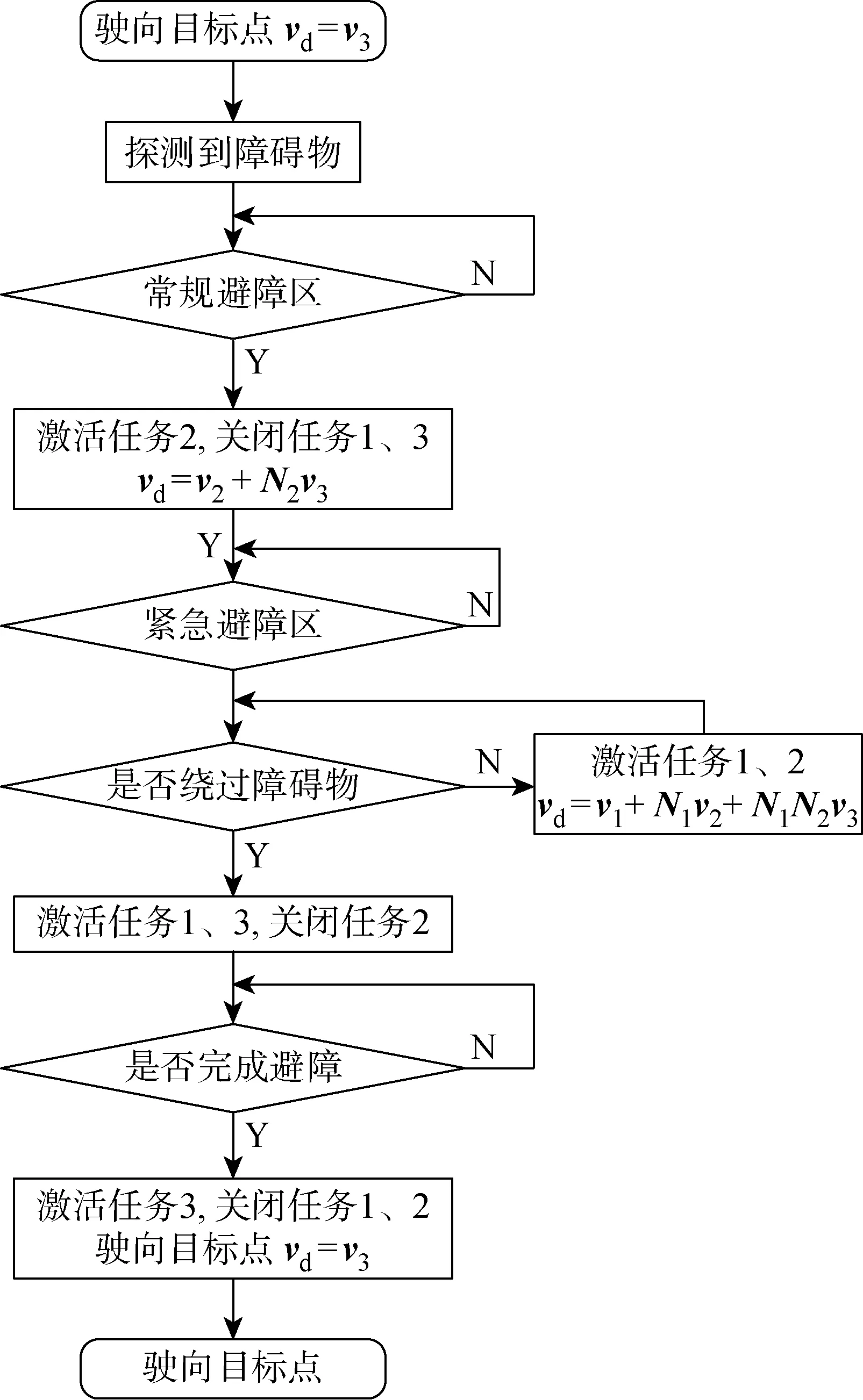
图8 NSB任务管理器控制逻辑图

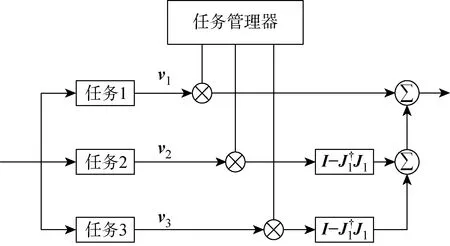
图9 NSB任务管理器工作示意图

3 模拟分析

为更加有效地阐述NSB法的避障效果，将基于行为法中传统的行为抑制法和加权平均法的避障效果与NSB法相比较，避障效果如图10所示.设AUV的初始状态、目标点坐标和障碍物位置信息分别为

ηs=[0 m 0 m 0°]T

ηt=[70 m 70 m -]T

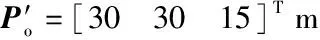
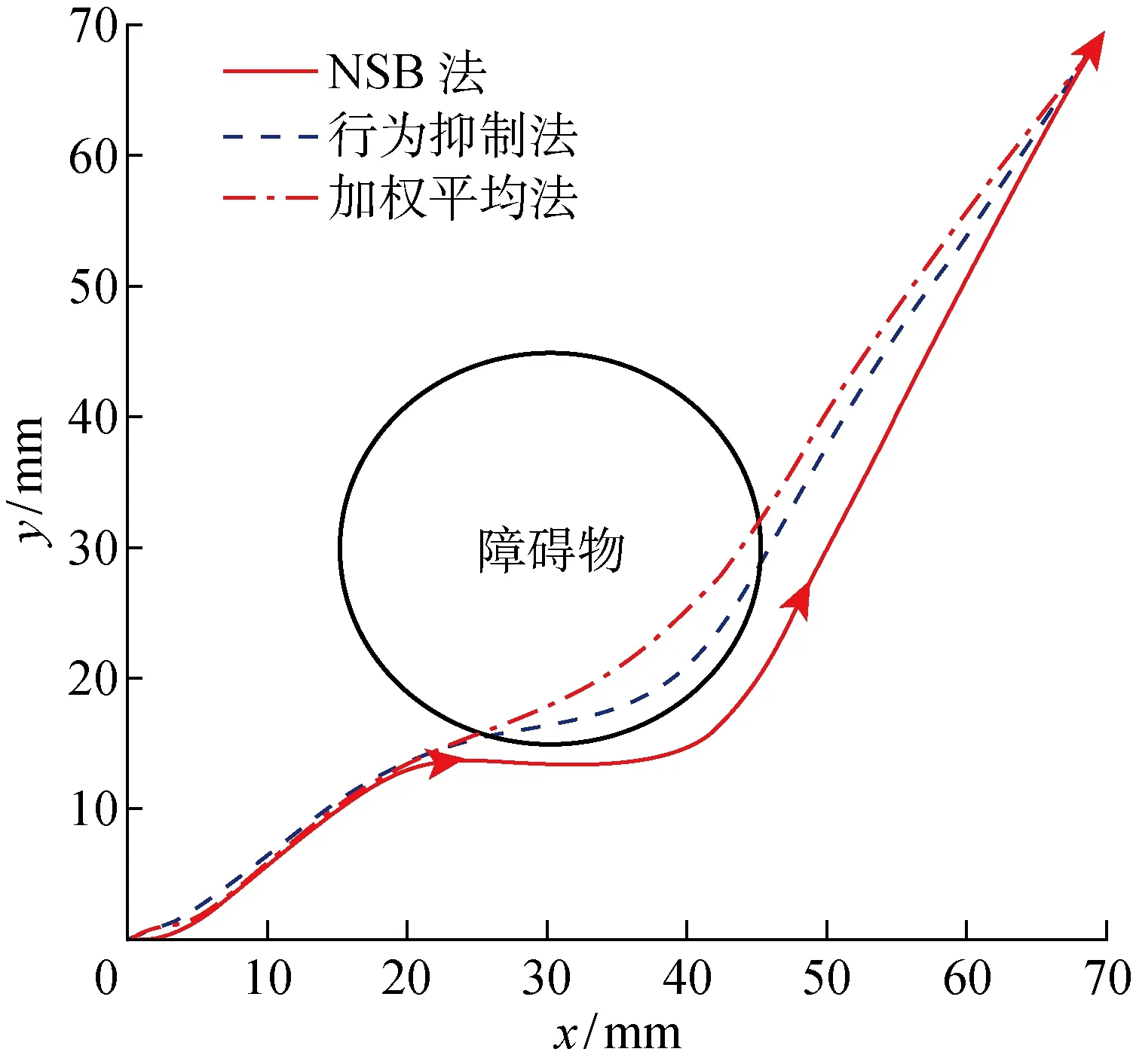
图10 不同方法避障效果对比图

其中前两个元素分别为障碍物的横纵坐标位置信息，最后一个元素为障碍物安全半径.从图中可以看出，对于静态障碍物，相对于行为抑制法和加权平均法的避障，基于NSB法的避障路径没有突入障碍物的安全范围，并且避障效果良好.说明NSB法按照设计方案，将低优先级的驶向目标点任务向较高优先级的避障任务的零空间投影，能够较好地处理不同优先级任务之间的冲突，并且最终圆满完成任务.而行为抑制法和加权平均法的避障路径中，有部分路径突入了障碍物的安全范围.如果障碍物的安全半径设置较小，AUV在驶向目标点的过程中很有可能与障碍物发生碰撞，这种情况一旦发生，不仅无法按预期完成任务，而且还会对AUV的自身安全造成难以预料的影响.合理推测，当面对动态障碍物时，行为抑制法和加权平均法的避障效果相对会更差.综合对比说明，NSB法相对于行为抑制法和加权平均法，有一定的优越性和实用性.在以上分析的基础上，以3种情况为例继续展开基于NSB法的避障效果仿真计算.

情况1首先设置4个静态障碍物，其中两个在AUV的路径范围内.因此，AUV在驶向目标点的过程中，必须绕过这两个障碍物，同时需要避免另外两个障碍物的影响.

设AUV的初始状态和目标点位置分别为

ηs=[5 m 7 m -57.32°]T

ηt=[160 m 130 m -]T

4个障碍物的位置坐标和安全半径分别为

模拟结果如图11所示.

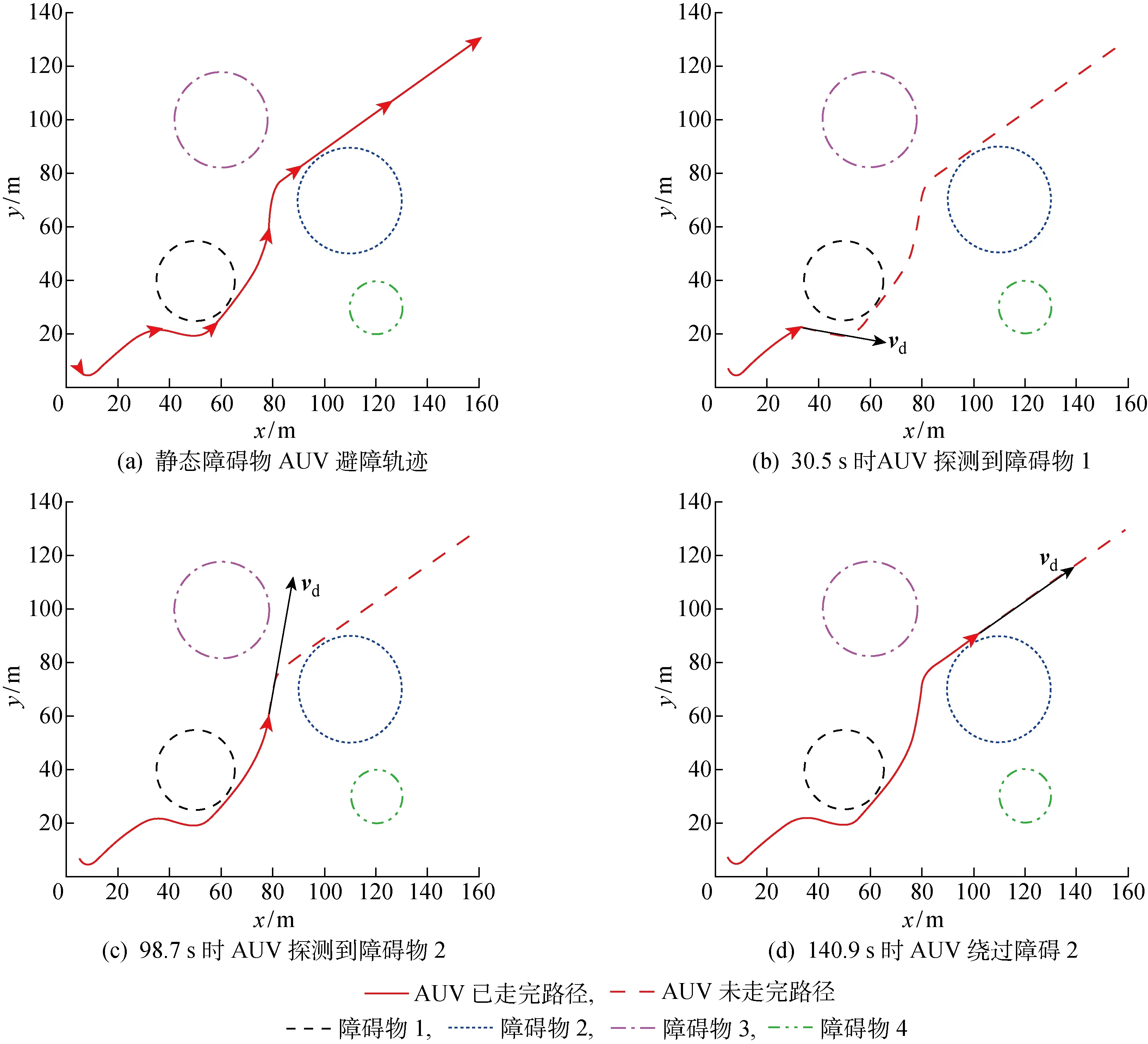
图11 静态障碍物AUV避障策略图

如图11(a)所示，AUV面对静态障碍物时能够及时避开障碍物并驶向目标点；如图11(b)所示，在30.5 s时AUV探测到障碍物1，启动避障算法，逆时针绕过障碍物；如图11(c)所示，在98.7 s时AUV已经绕过障碍物1继续驶向目标点，并探测到障碍物2的存在.相对于从障碍物2和4之间穿过，AUV从障碍物2和3之间穿过路径较短，因此AUV选择按顺针方向绕过障碍物2；如图11(d)所示，在140.9 s时AUV按照避障算法安全绕过障碍物2，驶向既定目标点，基于NSB的避障算法对静态障碍物避障效果良好.

情况2对于动态障碍物，本文设置了2个沿不同方向逼近AUV的动态障碍物，以考察NSB法对动态障碍物的应对能力.AUV在驶向目标点的过程中，需要实时探测相对于障碍物的距离和行驶方向，选择避开障碍物的最佳路线.

设AUV的初始状态和目标点位置分别为

ηs=[0 m -20 m 0°]T

ηt=[120 m 140 m -]T

两个障碍物的位置和安全半径分别为

障碍物的运动速度分别为

vo1=[-1.0 m/s 1.5 m/s 0°]T

vo2=[-0.8 m/s 0.8 m/s 0°]T

模拟结果如图12所示.

图12表明AUV基于NSB法的避障策略对于动态障碍物同样有效.如图12(a)所示为AUV在驶向目标点的过程中发现动态障碍物、绕过动态障碍物并最终驶向目标点的完整路线图.如图12(b)所示，在10.7 s时AUV探测到动态障碍物2，根据障碍物运动方向，选择以顺时针方向绕过障碍物，并在51.7 s时绕过障碍物2(见图12(c))；如图12(d)所示，在63.8 s时AUV在继续行驶途中发现动态障碍物1，同时启动避障算法；由图12(e)可以看出，在110.8 s时AUV以逆时针方向绕过障碍物1之后继续驶向目标点；图12(f)所示为AUV驶向目标点.

情况3当障碍物沿AUV正面运动方向相向运动时，被视为正面障碍物.当AUV在驶向目标点的过程中遇到正面障碍物时，需要判断相对于障碍物的行驶角度，并及时选择避开障碍物的方向(逆时针或顺时针).

设AUV的初始状态和目标点位置分别为

ηs=[5 m 7 m 57.32°]T

ηt=[150 m 200 m -]T

障碍物的初始位置和安全半径为

速度参数为

vo=[-1.0 m/s -1.2 m/s 0°]T

模拟结果图13所示.

图13(a)所示为遇到正面障碍物时AUV的避障轨迹图；如图13(b)所示，在43.7 s时AUV探测到障碍物，并根据相对行驶方向判断为正面障碍物，同时启动避障算法；如图13(c)所示，在68.4 s时AUV绕过正面障碍物；如图13(d)所示，在82.9 s时AUV逆时针绕过障碍物后继续驶向目标点，验证了NSB算法对正面障碍物避障的可靠性.

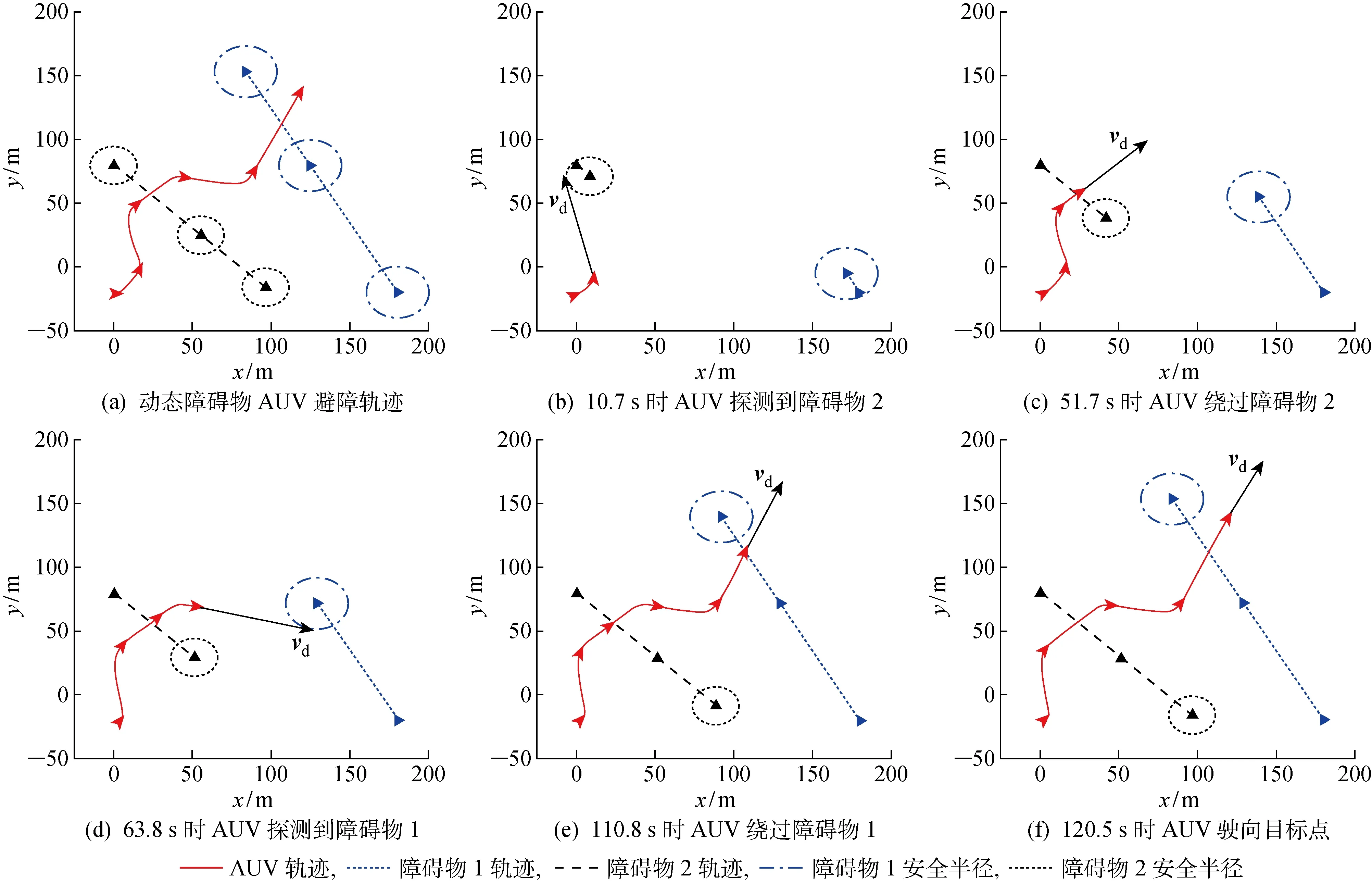
图12 动态障碍物AUV避障策略图

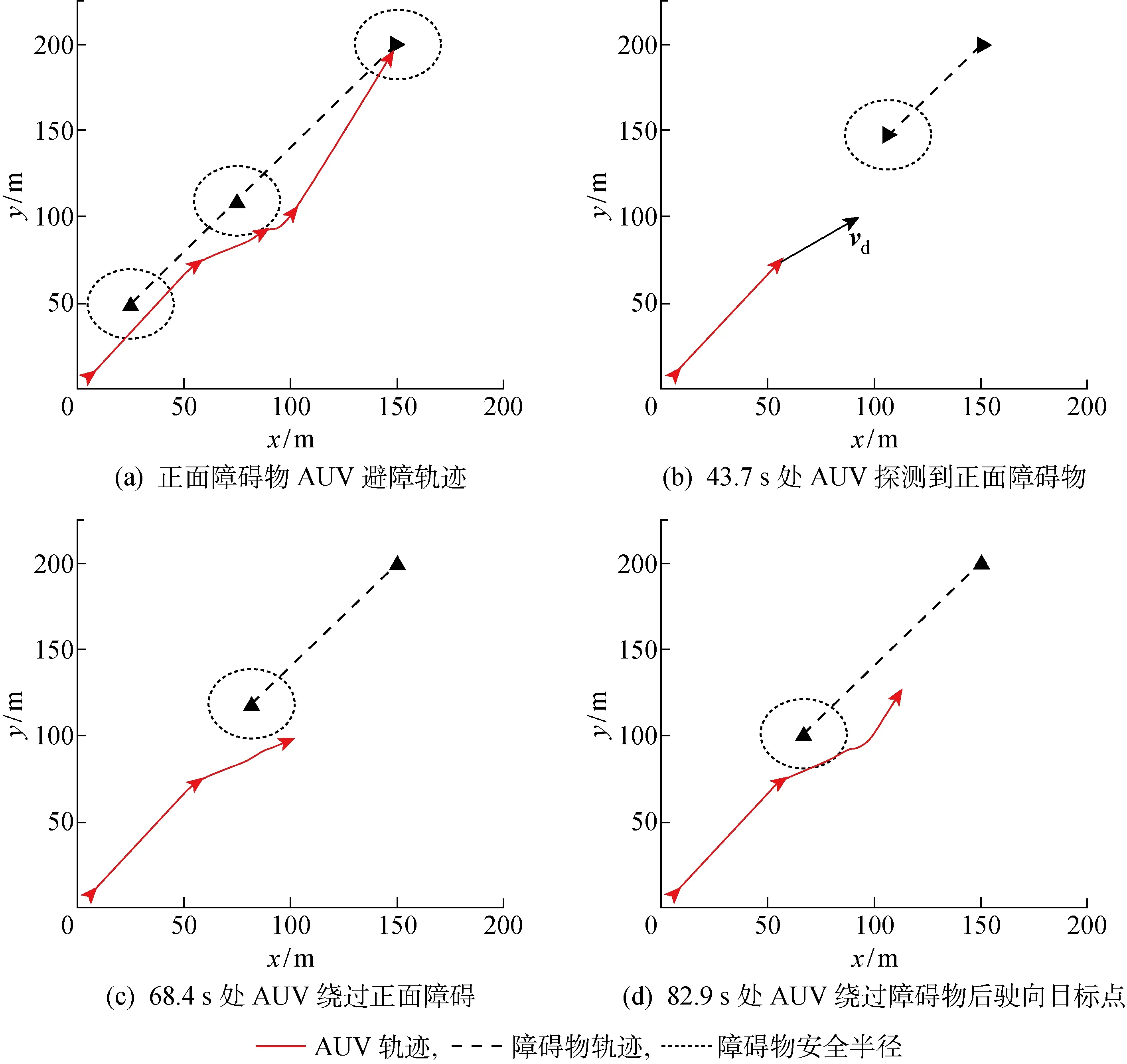
图13 AUV正面障碍物避障策略图

4 结语

本文基于NSB法，研究分析了AUV对于动静态障碍物的避障问题.对于多任务目标控制，NSB法能够有效避免各任务间冲突，出色完成避障任务.在介绍NSB法的基础上，针对AUV在驶向目标点过程中可能遇到动态和静态障碍物的情形，设计了不同的避障策略，把总体任务分解为不同等级的任务控制目标，建立了相应的输出函数，得到了AUV整体任务的函数输出模型.对于何时激活子任务，设置了任务管理器，以保证各控制目标顺利实现.最后利用AUV模型进行了仿真验证，结果表明：对于静态和动态障碍物，AUV均能够顺利绕过障碍物最终驶向目标点，达到预期目标，验证了该方法的实用性.

文中所设计的基于NSB法的AUV避障策略，结合实验室现有AUV编队控制(主从式(L-F)法，图论法等)的相关积累，可开展更加深入和多方向的研究，如将该方法运用到编队避障中，也可将NSB法拓展至三维空间，研究AUV或AUV编队在三维空间中的避障和路径规划问题.