基于人工势场和虚拟领航者的智能车辆编队控制
2020-04-08王树凤张钧鑫张俊友
王树凤, 张钧鑫, 张俊友
(山东科技大学 交通学院,山东 青岛 266590)
智能交通系统(ITS)作为交通系统的未来重要发展方向,能有效地缓解交通拥堵、事故频发和资源紧张等社会问题.而多智能车辆编队作为ITS发展过程中的重要研究内容,在兼顾道路交通安全的前提下,能充分利用道路容量,提高道路交通效率和车辆燃油经济性,因此成为交通发达国家研究和应用的重点[1].
人工势场法[2]作为智能体编队控制的常用方法,通过定义相应的人工势场得到相应的队形,且与领导者跟随方法、基于行为法[3-4]等算法相比较,算法简明,具有较高的灵活性和适用性,但易使编队对象陷入局部最小点[5].因此,文献[6-8]提出人工势场法和虚拟领航者相结合的编队模型,不仅解决了编队系统对领航者的依赖问题,而且消除了势场存在局部最小点的隐患.Sabattini等[9]通过引入定点势场来消除局部最小点,获得了不同的正多边形编队形状.随着智能体编队应用的不断发展,人工势场法在无人机编队[10-11]、水下车辆编队[12]、道路车辆编队等方面的应用也越来越广泛,其中智能车辆编队作为智能体编队拓展应用的研究热点,主要研究内容包括队形形成、队形保持等行为.针对人工势场法应用到道路车辆编队,Li等[13]基于人工势场提出简单的两车辆跟驰模型,实现了智能车辆的跟驰行为,但忽略了车辆的横向交互和道路尺寸约束对车辆编队的影响,因此无法保证模型适用于多车辆公路编队,上述编队模型的应用对象或者为智能体,或者编队环境为非实际道路环境.
本文以基于人工势场和虚拟领航者的4智能体编队模型为研究基础,以多智能车辆在公路环境中的编队为研究对象,分析了公路环境中车辆编队行为,考虑车辆动力学以及道路安全准则等条件约束,建立车辆编队的最小安全距离模型,提出虚拟领航者的椭圆形作用域,并以4车辆编队为例,确定虚拟领航者的具体作用范围,建立4智能车辆编队单元模型;并基于分解-迭代思想和道路实际条件,提出编队单元的纵、横向迭代,实现多智能车辆(车辆数量大于4)公路编队行为.为验证建立的车辆编队模型,使用MATLAB进行多智能车辆公路编队仿真验证.
1 多智能车辆公路编队行为分析
为更好地控制车辆编队行为,使之与理想编队行为一致,本文基于车辆公路编队约束条件和智能体编队模型提出智能车辆公路编队规划框架,如图1所示.

图1 编队规划框架
1.1 智能车辆编队目标
由图1可知,车辆公路编队约束作用于编队模型,从而使形成的编队达到目标要求.为更好地分析编队约束,首先应明确公路编队目标.
当车辆编队运行在公路环境中时,为提高道路通行效率,应实现以下行为[14]:
(1)车辆速度一致性,即车辆在遵守交通规则的前提下,各车辆速度大小、方向保持一致;
(2)车队距离保持理想值,即当车辆之间距离过大或者过小时,车辆自主进行距离调节;
(3)车队安全高效地从出发点到达目的地,即车队在遵守交通安全规则的前提下,其前进方向保证正确.
综上所述,车辆公路编队的目标为各车辆间速度一致,距离一致,即
(1)
式中:t为编队完成时间;th为编队形成时间;vi(t),vj(t)分别为t时刻车辆i,j的速度;qi(t),qj(t)分别为t时刻车辆i,j的位置;L为理想编队距离.
1.2 公路环境的安全约束
由上述公路编队目标可知,车辆编队不同于智能体编队控制,具有公路运行安全约束,主要包括道路条件的几何约束和车辆自身的动力学约束,约定x方向为纵向,即车辆行驶的方向,y方向为横向.
1.2.1道路尺寸条件约束 保证编队车辆之间不发生碰撞且不超出车道边界:
(2)
式中:Lx,Ly分别为相邻车辆的编队纵向、横向安全距离;qi,x,qi,y,qj,x,qj,y分别为第i,j辆车的位置在x,y方向的分量;Hu,Hd分别为车道的上、下边界.
1.2.2车辆动力学约束 保证编队车辆安全、平稳地行驶需满足:
(3)
式中:vmax为公路限速值;ax,max,ay,max分别为车辆在x,y方向的最大加速度,分别取值ug,0.5ug[15],u为道路路面附着系数,g为重力加速度.
1.3 编队距离的安全约束
由式(1)可得,L作为编队建立的基础,决定了编队的几何形状,在道路编队应用中分为纵向距离Lx和横向距离Ly.
1.3.1编队纵向安全距离 合适的车辆纵向间距不仅可以保证车辆编队行驶的安全性,提高公路的交通流量,而且还可以提高车辆的燃油经济性.由于本文中设定多智能车辆行驶路况为平缓路面,不考虑路面高度起伏对车队的影响,所以选用车辆固定间距模型[16],图2所示为智能车A,B分别在t0,t1时刻的距离示意图.t0为车辆A开始减速的时刻,可将其设为0;t1为车速从vA减速到vB时,两车之间距离为0对应的时刻,为两车不发生碰撞的极限情况;Lx,min为两车不碰撞的最小纵向安全间距;S1,S2分别为智能车A,B从t0到t1行驶的距离;l为车辆长度.

图2 固定间距模型示意图
从图2可以看出,保证两车不发生碰撞的极限情况为
S2+Lx,min≥S1
(4)
由式(4)得到保证后车A不与前车B发生碰撞的最小纵向安全间距Lx,min为
(5)
式中:vA(0),vB(0)分别车辆A,B在t0时刻的速度;aA(t),aB(t)分别为车辆A和B在t时刻的纵向加速度;t,η为时间.
为提高编队车辆行驶安全性,在最小纵向安全距离基础上增加安全因子,即
Lx=ζLx,min
(6)
式中:ζ为距离调节因子,取值为1.2.
1.3.2编队横向安全距离 在交通规则的约束下,智能车辆应在各对应车道内行驶,理想情况下智能车辆应沿车道中心线行驶.而车辆宽度相比道路宽度不能被忽略,因此编队横向距离为
Ly=H-c
(7)
式中:H为公路的车道宽度,一般取值为3.5 m;c为车辆宽度,一般取值为2.5 m.
2 基于人工势场和虚拟领航者的车辆编队模型
为使车辆编队模型规划出的编队行为满足编队约束,结合上述分析,对基于人工势场法和虚拟领航者的智能体编队模型进行改进.
2.1 多智能体编队模型
人工势场法作为一种虚拟力方法,其基本思想为建立不同的势场来控制被控对象的运动.文献[7]在人工势场的基础上,引入虚拟领航者联合控制多智能体编队的形成,具体编队模型如图3所示.
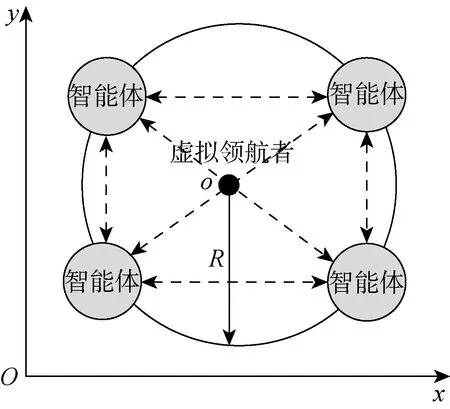
图3 智能体编队控制模型示意图
图3中虚线表示势场力作用,智能体i受到的势场力ui表示如下:
(8)
式中:b为一个实现系统阻尼作用的正数[7].式(8)中fv-l为虚拟领航者势场力:
其中:Kv-l为正增益系数;dv-l为智能体和虚拟领航者之间的距离;R为编队外接圆半径;rv-l.式(8)中fv-v为智能体势场力:
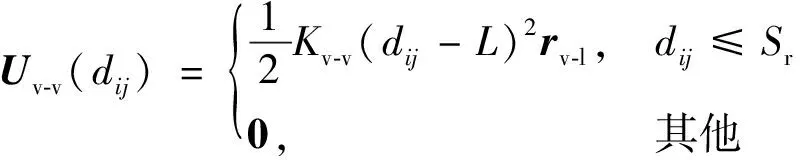
其中:Kv-v为正增益系数;dij为第i,j智能体之间的距离;Sr为智能体感知范围半径.
因此,上述编队模型使多智能体产生以下行为:
(1)势场Uv-l控制各智能体驶向以虚拟领航者为圆心,半径为R的圆周;
(2)势场Uv-v控制各智能体之间的相对距离;
(3)在两种势场共同作用下,4智能体最终形成理想编队.
2.2 4车辆编队模型的建立
上述编队模型应用对象为4智能体编队,因此其应用于智能车辆编队时存在以下不足:① 编队模型没有考虑道路条件的限制;② 编队模型不适用于多车辆(车辆数量大于4)编队.因此本文基于车辆道路编队行为,对该编队模型进行改进.
2.2.1改进的虚拟领航者作用范围 由于4智能体编队模型中的虚拟领航者的作用范围为圆形区域,使得编队的形成方位不确定,同时如果编队车辆数目较多,将导致虚拟领航者半径过大,而受道路尺寸的限制,这些因素都会给车辆编队在道路中的行驶带来安全隐患.
为使形成的车辆编队与公路尺寸及编队距离约束相匹配,基于两者在纵、横方向上的差异,对虚拟领航者的圆形作用区域进行改进.在x方向上,增大势场作用的距离;在y方向上,势场作用距离则变小,因此改进后的势场作用域由圆形变成了椭圆.根据椭圆的定义,设在x,y方向上,虚拟领航者势场作用距离为a和b.因此势场Uv-l变为
(9)
式中:dv-l=‖qi(t)-c1‖+‖qi(t)-c2‖,c1,c2分别为椭圆作用区域的焦点位置.
由式(9)可得改进后的虚拟领航者作用示意图,如图4所示.由于势场Uv-l控制各智能车驶向以虚拟领航者为圆心的椭圆周上,为保证车辆行驶满足交通法规约束,基于虚拟领航者的椭圆作用范围和编队距离的对称性,设定虚拟领航者沿车道边界线运动.
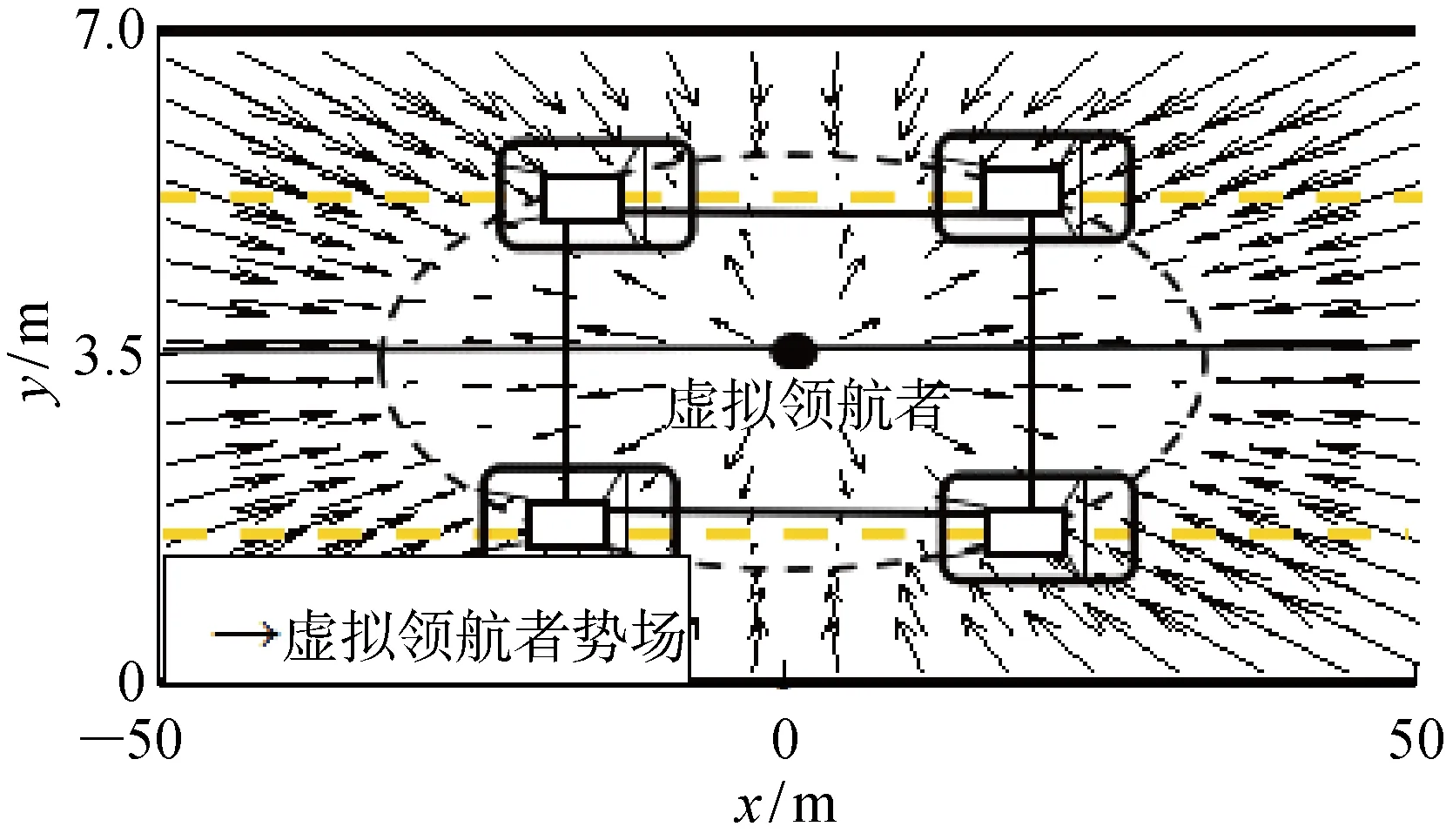
图4 改进的虚拟领航者势场模型示意图
虚拟领航者沿车道分界线前进且其作用范围由圆形区域改进为椭圆区域,使得编队模型无需增加额外势场就可以解决编队系统自身在虚拟领航者圆形作用域具有旋转自由度的问题,保证了编队前进方向的准确性和智能车辆在编队过程中满足道路条件的限制.

(10)
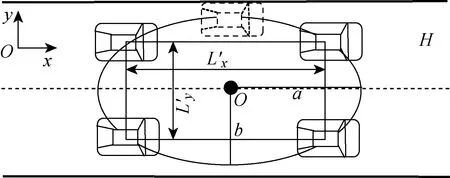
图5 车辆位置与椭圆区域的关系图
因此,虚拟领航者的椭圆作用范围具体表示为
(11)
式中:b∈(L′y/2H-c/2];L′y=Ly+c.
由式(12)可得,虚拟领航者的作用范围与编队距离、车宽、道路宽度密切相关.在实际应用中,可通过调节虚拟领航者的作用范围调整编队车辆的位置,以适应交通状况的变化.
2.2.3模型稳定性分析 综上所述,4智能车辆编队模型为
(12)
由Lyapunov函数得出编队模型系统总能量为
V=
(13)
由上述势场函数定义可知V是非负数,且只有当智能车车队形成理想队形时,V=0.而考虑该函数的时间导数:
(14)
由式(8)和(12)可推出
(15)
则有:
(16)

由LaSalle不变性原理[7]可以得到:已经临近稳定并且无耗散的平衡状态将以这种无耗散形式达到渐进稳定.
2.3 编队单元的迭代应用
由于虚拟领航者势场作用范围改进为椭圆形区域,使得上述编队模型只适用于4车辆编队.而针对多车辆编队(车辆数量大于4)问题,本文基于微积分的分解-迭代思想,通过增加虚拟领航者把编队车辆分解为相同的基本编队单元,每个编队单元由4车辆和1虚拟领航者组成,而基本编队单元又通过虚拟领航者之间的迭代串联形成编队.其具体原理如图6所示,其中基本编队单元由虚线所连接的车辆和1个虚拟领航者构成.

图6 编队单元迭代示意图
基于实际道路特点和编队要求,编队单元既可以横向串联,也可以纵向串联,因此可组成不同形状的编队,提高了模型的应用灵活性.同时,编队迭代单元只需保证单元内车辆位置的准确性就能确保编队的准确性,减少了模型的应用计算时间.此外,公路的曲率半径一般较小,在弯道上行驶的编队车辆,在其迭代单元范围内可近似认为车道为直道.因此对编队车辆进行分解-迭代处理,保证了编队车辆位置的准确性,无论编队车辆数量多少,公路线形如何,都可以有效准确地控制编队的队形,提高编队模型的应用灵活性.
3 仿真实验与分析
为验证提出的智能车辆编队模型所规划的公路编队是否合理,利用MATLAB进行车辆编队路径仿真.设定编队路径仿真运行路况为三车道路况,车道宽度为3.5 m,车道限速为80 km/h,路面附着系数为0.75,并设定虚拟领航者匀速运动,其速度为50 km/h,初始位置分别为(-30,0)和(-80,0)m,编队车辆初始状态参数如表1所示.

表1 编队车辆状态参数
为了更好地观察车辆编队的形成,把编队形成过程在全局坐标系中体现出来,如图7(a)所示,6辆智能车辆在编队模型的作用下,逐渐形成理想编队形状.而图7(b)和7(c)则是两编队迭代单元的路径形成过程.

图7 理想编队的形成过程
以第一编队迭代单元路径仿真为例,阐述车辆编队的形成.如图7(b)所示,编队开始时,各智能车辆初始位置不满足理想编队要求,受到势场Uv-v和Uv-l的共同作用,1车道的车辆(车辆1和车辆4)慢慢驶到2车道,3车道的车辆(车辆2和车辆3)则向道路中心线方向行驶,直至各车之间的距离达到理想编队距离,同时跟随虚拟领航者向前行驶.
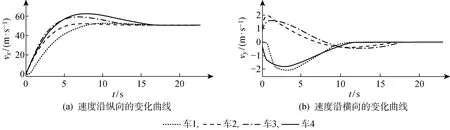
图8 智能车编队过程中的速度变化曲线
图8为第一个迭代单元的车辆在编队形成过程中速度的变化曲线.从图8可以看出,车辆在编队形成过程中速度从0变化至50 km/h,最终与虚拟领航者的速度达成一致.由于车辆受车辆最大纵向以及侧向加速度的限制,其速度变化有一定的差异,但是变化趋势平缓,在满足车道要求的基础上,也满足车辆的动力学要求.
后一编队迭代单元车辆速度变化趋势和前一迭代单元基本类似,也满足车辆约束和道路约束.本文不再对其进行详细阐述.
由以上编队仿真结果可知,采用改进的编队控制模型规划的编队路径,满足车辆动力学约束与道路约束,符合车队编队目标要求.
4 结论
(1)根据车辆公路理想编队行为特点,提出了虚拟领航者势场的椭圆形作用区域,建立了4车辆编队单元模型,保证了车辆满足编队安全约束,并通过Lyapunov函数证明了模型的稳定性.
(2)基于多车辆(车辆数量大于4)编队,依据分解-迭代思想提出编队单元的纵、横向迭代,确保了编队车辆位置的精确性,提高了编队模型的应用灵活性,并通过多车辆编队仿真结果证实了编队控制模型的有效性.
