浸没及非浸没刚性短植被群对异重流运动特性的影响

熊 杰， 袁野平， 林颖典

(1.浙江大学 海洋学院，浙江 舟山 316021；2.中国建筑第三工程局有限公司，武汉 430073)

异重流又称密度流，指密度差异使得一种流体沿着交界面流动，且在流动过程中不与其他流体发生全局性掺混的现象[1].异重流按密度差异的形成原因可分为2类：组分驱动异重流和颗粒驱动异重流[2-3].

在自然环境和实际工程中，植被可以显著影响异重流的运动过程[4]，影响程度取决于植被特性，如刚性植被(植被形变可以忽略)和柔性植被(植被形变不可忽略)，或浸没式植被(植被高度小于水深)和非浸没式植被(植被高度大于水深)[5-6].目前室内实验与数值模拟是研究异重流较为常见的手段，可直观地显示各参量的变化，国外已取得诸多成果.Tanino等[7-8]研究开闸式异重流在随机排列植被作用下的运动特性，观察到2种不同的运动形式：异重流与环境水体呈线性界面(三角形轮廓)和非线性界面(典型轮廓，为半椭圆形头部及掺混剧烈的长条形尾部).其中，由于植被阻力相对于惯性力和黏性力而占主导作用，异重流演化为三角形轮廓，与多孔介质中的“两层”流动形态极为相似[9].Zhang等[10]通过室内实验和理论分析得出结论，异重流流入植被后的头部速度随时间逐渐减小并且与流入植被的体积成正相关.Testik等[4]通过实验研究发现持续入流式异重流流经非浸没式植被时会进入阻力阶段，头部演化为三角形轮廓并且角度趋于定值.Cenedese等[11]发现，异重流流经规则排列浸没式植被(密度为9.0%)时，因流动过程中圆柱体尾迹形成涡量加强掺混，在流过植被(密度为35.0%)时因瑞利-泰勒(R-T)不稳定性加强掺混.Zhou等[12]通过大涡模拟研究浸没式植被对异重流运动特性的影响，发现异重流在坍塌阶段头部速度随植被密度增大呈现先增大后减小的变化，并且在不同排列方式(线性排列和交错排列)植被下存在4种运动形态(贯穿流、溢出流、倒转流、层间流).目前国内在植被对异重流运动特性影响方面的研究极少.

刚性植被对异重流运动特性的研究主要集中在长植被群对异重流头部速度、头部形态、浓度结构等宏观方面的影响，而关于短植被群对异重流的影响以及流入植被时异重流内部的速度场和涡度场等微观结构研究甚少.在实际工程中，植被区域附近的微观结构对探明植被对异重流影响的机理具有十分重要的意义.

本文利用实验手段，综合考虑短植被群密度和高度的影响，对因密度差异形成的开闸式异重流进行水动力学特性研究.实验中采用高速摄像机记录异重流发展过程，获取头部位置、头部速度和形态特征，利用粒子图像测速技术(PIV)获得异重流流入植被时的速度场、涡度场及特征断面速度和涡度变化，为植被作用下污染物扩散和物质运输研究提供科学参考依据.

1 实验装置及步骤

开闸式异重流实验在长200 cm，宽20 cm，高20 cm的长方体有机玻璃水槽中完成，如图1所示.H为水深，闸门置于距离水槽右端10 cm处且采用步进电机控制，能够消除人工启闭闸门引起的扰动和偶然误差的影响.为使异重流匀速阶段流经植被区域[5]，植被放置距离闸门右侧40 cm处，即4个闸门长度，此时异重流处于匀速阶段.植被简化为直径D=7 mm的刚性木质圆柱体，采用3种不同的植被高度(Hv=3，6.5，16 cm)，并将植被固定在长(Lv)30 cm和宽(Wv)20 cm的有机玻璃板上，即植被群大小为30 cm×20 cm.环境水体和异重流同时分别注入闸门左侧和右侧水槽内，当水槽两侧液面高度H达到14 cm时，停止注水.等待水槽内水体静止时开启闸门，闸门采取加速上升方式且运动时间为0.2 s，异重流坍塌并沿着水槽底部向前运动，环境水体在其上方作相反方向运动[13]，异重流到达水槽末端时实验结束.

采用高速摄像机拍摄异重流的运动过程，均采用标定板进行水平和垂直标定，将1台Nikon摄像机(机1)架设于水槽前方100 cm处侧向拍摄异重流立面二维全程运动现象，该CCD摄像机分辨率为 1 920 像素×1 080 像素，帧率为25 帧/s.异重流流入植被过程中的速度场、涡度场及特征断面变化等数据通过PIV获得，拍摄范围处于距离闸门20～60 cm处.该系统包含1台垂直于植被放置的CCD摄像机(机2，分辨率为 2 320 像素×1 726 像素，帧率为100 帧/s)和1个平行于水槽中心线的激光器(波长为532 nm，扩散角为45°).

实验在室内25 ℃恒温进行，通过分析清水和盐水的温度差异，两者温差最大值为0.07 ℃，可以确定实验中异重流产生是由密度差引起的，温度差异形成的异重流可以忽略不计.

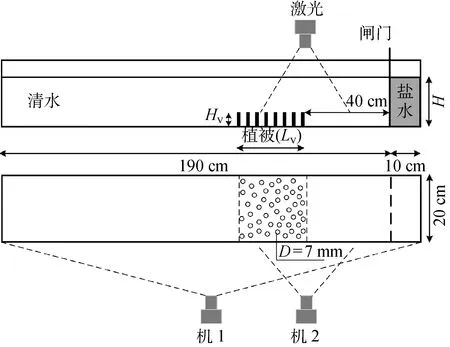
图1 开闸式异重流实验水槽设置

2 实验工况及条件

为确保实验的可比性，消除量纲对实验结果的影响，对实验中部分参数进行无量纲化处理.流体之间密度差异是产生异重流的根本原因[1]，本文采用有效重力加速度[13]描述差异，其定义为

g′=Δρg/ρ0

(1)

式中：Δρ=ρ1-ρ0，ρ1为异重流密度，ρ0为环境水体密度；g=9.81 m/s2，为重力加速度.

描述异重流运动状态[11]的雷诺数以及惯性力与重力相对大小的弗劳德数为

Re0=uTH/ν

(2)

(3)

式中：uT为异重流头部全程平均速度；ν为水的运动黏滞系数，取值10-6m2/s.

植被单位面积内所占比例可表示为RSPF, 计算公式为

RSPF=NπD2/(4LvWv)

(4)

式中：N为植株数目.

以H和特征时间tc=H/(g′H)1/2为参量，对异重流头部位置x、头部速度u、头部高度h和时间t进行无量纲化：

(5)

表1给出异重流运动的实验参数：除工况1为无植被存在，其余工况均为Lv=30 cm；采用无量纲植被高度hv=Hv/H，非浸没式植被hv取1.00.实验中异重流均采用食用盐配置，浓度均为S=1.55%(无量纲化参量浓度S为盐水中溶解的食盐与盐水质量之比)，实验中各组雷诺数均大于 1 000，认为异重流为湍流流动，黏性作用对实验结果影响不显著[14].

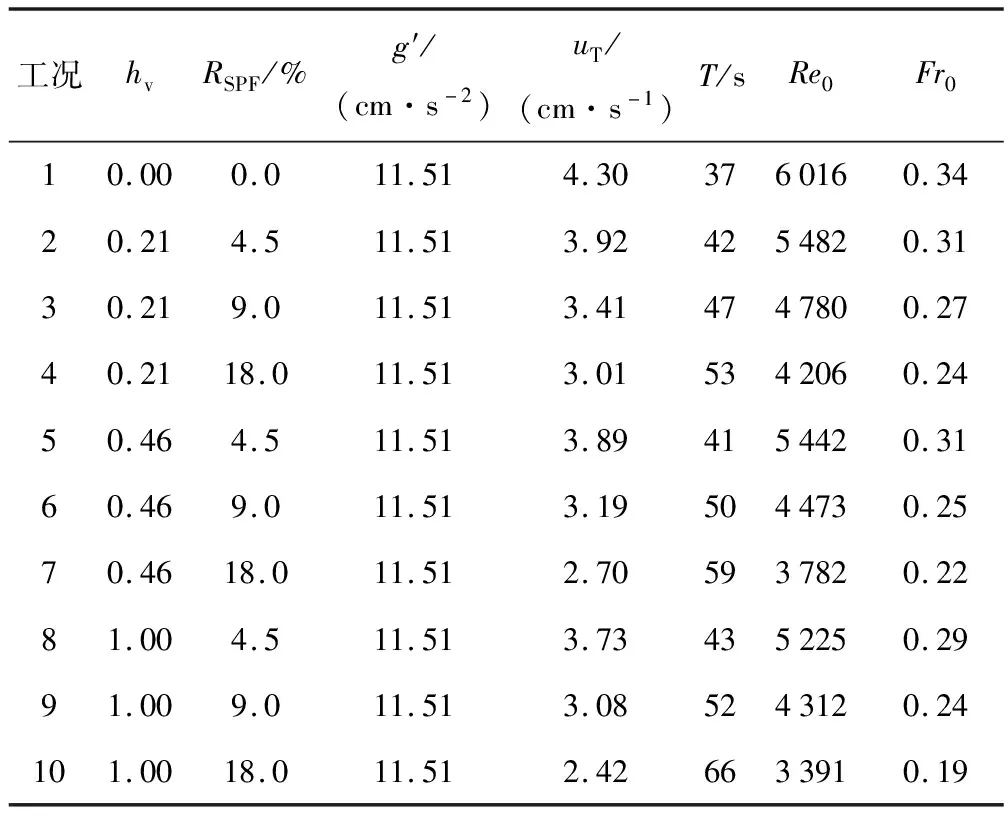
表1 实验工况及参数

3 实验结果及分析

3.1 形态分析

异重流在闸门开启后会沿着水槽底部向前运动，在流经不同密度和高度的植被时，形态发生改变，如图2所示.异重流在沿着光滑底床流动时头部高度约为H/2[15]；当hv=0.21时，异重流在流经植被时头部高度稍有抬升，头部高度大于H/2；当hv=0.46时，异重流头部典型形态消失，演化为三角形轮廓，部分流体会在植被顶部向前流动(图2(f))；当hv=1.00时，异重流在植被间运动，头部轮廓趋于平滑并且演化为三角形轮廓(图2(i))，与文献[8]观察结果一致.

图2 异重流遇到植被时形态变化

当hv=0.21时，异重流在流经不同密度植被时与流体在两层多孔介质中流动的形态极为相似[16].在RSPF=4.5%(图2(a))和9.0%(图2(b))时，异重流依然保持半椭圆头部形态，下层流体在植被间运动，上层大部分流体在植被顶部流动，类似于在粗糙度较大的底床上运动，植被间的流体由于植被的阻挡效应，流体速度减慢，与周围流体的掺混减少，即开尔文-亥姆霍兹(K-H)涡减少，湍动能减小.植被上部流体上界面与环境水体发生挟带和掺混，下界面向下坍塌并补充到植被内部流体中去，将势能转化为动能，维持异重流继续向前运动.对于RSPF=18.0%(图2(c))，异重流流入植被时出现2个头部并且分层向前运动，两者速度几乎保持一致，由于高锰酸钾与盐水有很好的相容性，所以水体颜色可以清楚地反映异重流浓度的变化；通过观察可以发现植被内部异重流颜色较植被上部更浅，因此可以认为异重流植被区域流体密度比植被上部密度低.异重流上部区域流体的上界面与环境水体间会产生K-H不稳定[17]，使上部流体因挟带和掺混作用而被稀释；下界面由于植被上部流体较植被内部流体密度大而产生R-T不稳定性，从而与下部流体发生交换[11]，向下输入动能维持下部区域异重流向前流动的能量.

当hv=0.46时，对于RSPF=4.5%(图2(d))和9.0%(图2(e))，由于植被抬升，高出植被的流体可迅速滑塌至植被间运动，所以异重流几乎全部在植被间运动，头部速度降低，与环境水体掺混作用减弱，形成K-H涡不显著，交界面趋于平滑，湍动能减少.对于RSPF=18.0%(图2(f))，异重流分为两层在植被内部和顶部运动，大部分异重流在植被内部运动并且因植被抑制掺混而形成三角形轮廓，少部分异重流要克服重力势能跃上植被并在顶部向前运动，在新的“底部边界”上运动时底部粗糙度更大，导致头部速度较慢，造成头部速度小于植被内部异重流头部速度，形成两层流动.

当hv=1.00时，异重流均在植被间运动，植被密度越大，异重流被抬升的高度越大，界面更加平滑且阻挡在植被后方的体积更多.

3.2 头部位置

x*=u*t*

自相似阶段拟合公式为

x*=a(t*)b

其中：a、b为拟合参数，b代表x*和t*数据线性化后的拟合直线斜率，斜率越小代表头部速度越小.

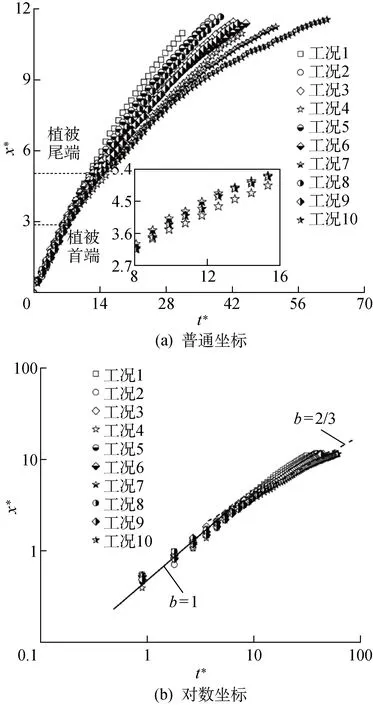
图3 异重流无量纲头部位置随时间变化关系

表2 实验工况及拟合参数

对于滑塌阶段，工况1中xt=94.36 cm，约为10倍闸门长度，与文献[5]结果一致，而植被的存在可以使异重流的转换点前移；当hv=0.21和0.46时，转换点与植被密度成负相关，植被密度大时植被高度对转换点的影响表现为使之显著性前移；当hv=1.00时，转换点xt=(42.70±1.00)cm，即异重流刚进入植被就进入自相似阶段，植被密度对异重流转换点影响不显著.究其原因，实验中存在非浸没式植被时，植被代替了水槽左侧边壁，异重流运动过程中产生内波可被植被反射而向相反方向运动，迅速抵达异重流头部位置，加上植被的阻挡效应，两者共同作用可以显著使转换点前移.所有工况中u*=0.40±0.02，u=(5.09±0.30)cm/s，可以认为植被的存在使转换点的位置前移，但对滑塌阶段头部速度影响不显著.

自相似阶段的异重流头部速度随时间变化而逐渐减小，工况1中b=0.73，比文献[5]中2/3偏大，是因为水槽底床摩擦力不同.由表2可知，当hv=0.21时，工况4与工况2中b相等，较工况3中更大，原因为工况4中异重流的转换点x*=3.74，在植被后约12 cm，而后异重流向下坍塌，势能转化为动能，此阶段的存在导致b取值较大；当hv=0.46，1.00时，b与植被密度成负相关，植被密度越大，则b值越小，原因在于植被密度越大，对异重流阻挡效应越显著，异重流动能耗散越大，头部速度递减越快.当RSPF=4.5%，9.0%时，本研究中的b值与植被高度成负相关，原因在于植被高度越大，对异重流的阻挡效应越显著；非浸没式植被的b值最大，原因在于植被密度较小时，植被高度变化对异重流的阻挡效应不显著，并且异重流流过非浸没式植被时不再受内波的影响，此时植被代替水槽右侧边壁，阻挡内波向前运动，速度递减变缓.当RSPF=18.0%时，b值与植被高度成负相关，因为当植被密度较大时，植被对异重流的阻挡效应占主导作用，而此时植被高度越大，阻挡效应越明显.

为了进一步分析植被对异重流的阻挡效应，表3列出异重流在植被区域及其前、后的特性参数.表格中ub，uv，ua分别为异重流头部在植被前(0～40 cm)、植被区域(40～70 cm)、植被后(70～160 cm)的平均速度.速度减幅N1及N2分别代表流过植被群后，异重流头部速度减幅及异重流头部到水槽左端的速度减幅：

N1=(ub-uv)/ub，N2=(ub-ua)/ub

由表3分析可得，植被高度越大，密度越大，对异重流的阻挡效应越强，异重流减速越显著.观察工况3和工况4，N1值较其他工况大，而N2值并不显著.当hv=0.21时，异重流流过植被时头部速度减小是植被对异重流的阻挡效应和异重流被抬升导致动能转化为重力势能两者共同作用的结果，N1值较大；而后异重流继续向前运动，重力势能转化为动能，植被阻挡效应类似加大底床粗糙度，减速效果不显著，导致N2值较小.当hv=0.46，1.00时，异重流头部受到植被阻挡时，会通过减小与环境水体的掺混速率，使异重流头部速度递减变慢，N1值较小；然而植被高于异重流厚度，对异重流整体阻挡效应显著导致能量耗散较大，N2值较大.

表3 异重流区域速度

3.3 掺混系数

异重流的掺混机制对动力特性研究至关重要.Morton等[18]假设掺混速率与头部速度成正比，掺混系数为

E=we/u

(6)

式中:we为掺混速率.

通过MATLAB获取头部位置与时间的关系后计算出u，再进一步获取瞬时速度.然而，至今尚无直接计算we的有效方法.Jacobson等[19]通过考虑二维侧面面积的变化研究空间平均掺混速率，得到

(7)

式中：A为异重流侧视图面积.当异重流完全流出闸门后开始计算，若异重流流入植被，则侧视图面积折减为A=A1(1-RSPF)+A2，A1为植被内部异重流侧面面积，A2为植被外部异重流侧面面积.

为了精确分析植被对异重流掺混系数和掺混速率的影响，研究区域取闸门至植被后约100 cm处(0≤x*≤12).图4所示为异重流掺混速率与头部位置及头部速度之间的关系.由图4(a)可见,对于工况1(不存在植被)，掺混速率随头部位置递减，在x*=7～12时，we约为0.01～0.02 cm/s.当植被存在时，在流入植被之前，异重流掺混速率随头部位置迅速递减；而后由于植被的阻挡效应，掺混作用减弱，掺混速率趋于线性递减；流过植被后掺混速率随头部位置缓慢递减并且趋于0.当hv=0.21时，掺混速率较其他有植被工况更大，究其原因，一方面是部分异重流在植被上部运动，与环境水体接触面积增大，掺混速率增大；另一方面由于R-T不稳定性，植被上部和内部异重流持续交换，掺混速率增大.由图4(b)可见，掺混速率在坍塌阶段初期与头部速度关系不显著，但当异重流从坍塌阶段调整至自相似阶段后，与头部速度呈现线性递减关系，这和Jacobson等[19]结果相近.在线性阶段，可得出线性回归方程(R2=0.638)为

we=au+b

(8)

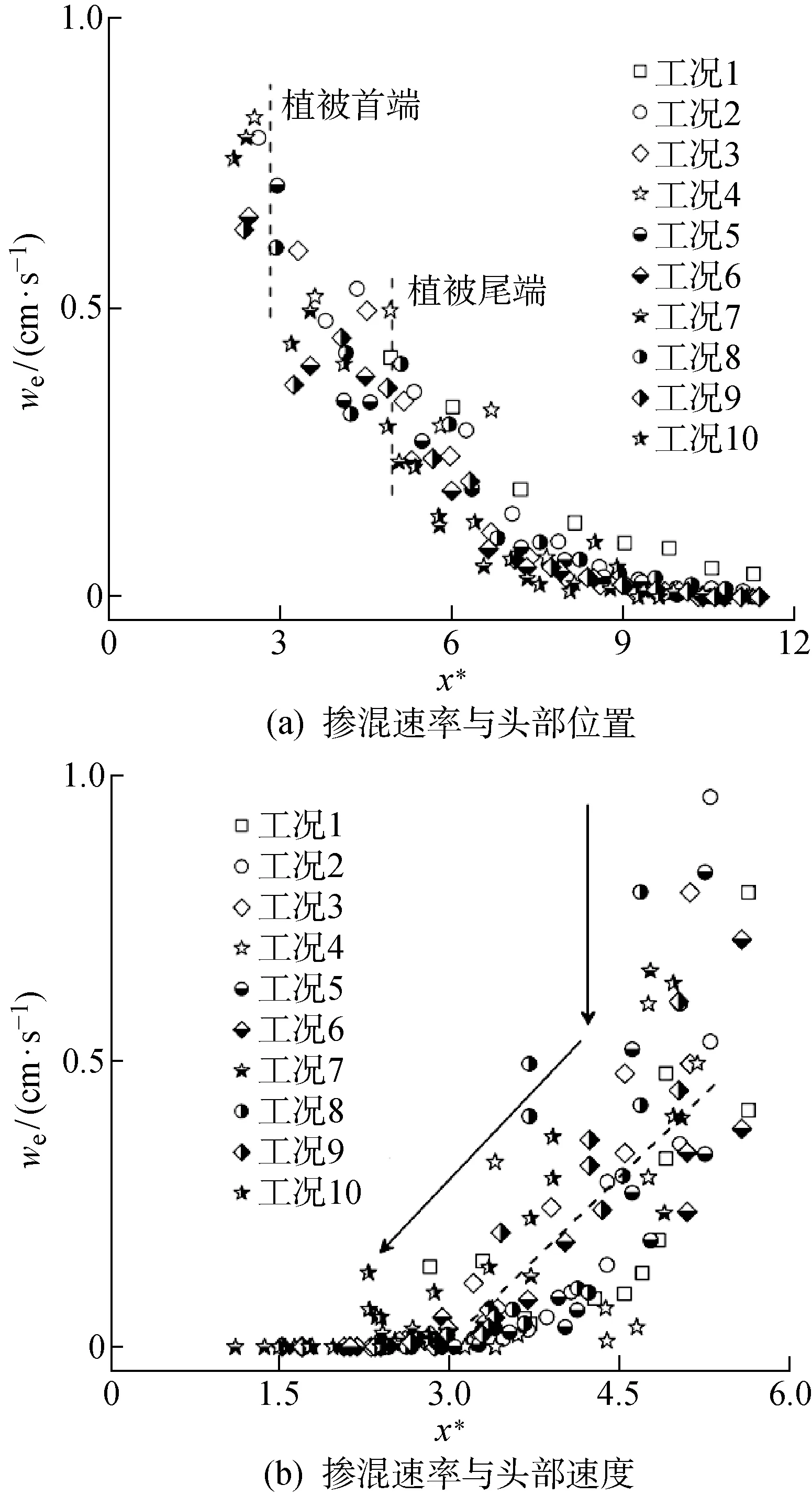
图4 异重流掺混速率的变化

式中：a=0.171 cm/s；b=-0.484 cm/s.a和b这2个经验常数通过实验中的掺混速率和头部速度关系拟合得到.文献[18]中a=0.044 cm/s，b=-0.035 cm/s，认为实验中植被群的存在影响了头部速度和掺混速率，导致掺混速率随头部速度递减变快，故a值较大.当a=0时，we=-0.484 cm/s，异重流静止时会被环境水体稀释因而掺混速率为负值.因此，式(8)适用于异重流处于自相似阶段且头部速度低于某临界值时掺混速率可忽略不计的情况.

掺混系数通过式(6)计算得到，与头部位置的关系如图5所示.掺混系数随头部位置逐渐减小，对于工况1，在x*=3～5时，E≈0.10～0.15.对于不同高度植被而言，当hv=0.21时，植被的阻挡效应导致异重流运动速度减慢，掺混受到抑制，掺混系数减小，但是部分异重流能够在植被上部运动，上界面与环境水体掺混和下界面R-T不稳定性的影响导致掺混系数增大，两者拮抗作用导致掺混系数减小不显著，此时x*=3～5，E≈0.10～0.13；当hv=0.46，1.00时，异重流几乎全部在植被内部运动，受植被阻挡效应显著，导致掺混系数较小，此时x*=3～5，E≈0.06～0.11.在x*=7～12时，对于无植被的工况1，E≈0.02～0.06，而对有植被工况，E≈0～0.02，平均掺混系数仅为工况1的25.0%，短植被群可显著抑制异重流的掺混；对于不同密度植被而言，植被密度越大，单位面积圆柱体数量越大，与异重流接触面积越大，阻挡效应越显著，掺混系数越小.

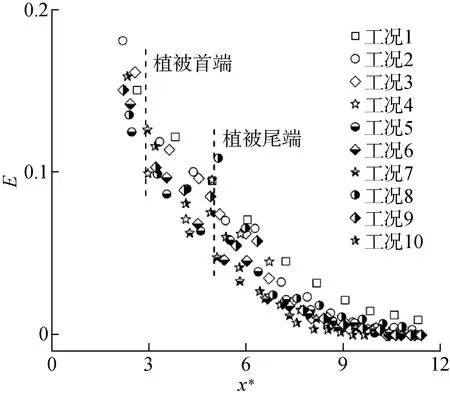
图5 异重流掺混系数与头部位置的关系

3.4 速度场和涡度场

利用PIV系统记录异重流流入植被的微观速度场和涡度场变化过程.在工况3时异重流头部位置到达植被时刻及其前1 s和后1，2，3 s时的局部形态、流场图和涡度图，将异重流头部到达植被时刻定义为t=0，如图6所示分别为t=-1 s，t=0及t=1，2，3 s时的情况.由图6(a)可知，在异重流头部未到达植被之前，由于底部无滑移边界条件和上部边界剪应力共同作用，可清晰地显示异重流头部前方有一个略微抬升的“鼻子”，这和文献[17]相符合.由于异重流与环境水体存在速度剪切和密度剪切作用，所以会在交界面上剧烈掺混而形成典型的K-H不稳定现象.随着异重流继续向前运动，部分沿着水槽底部在植被间运动，大部分被抬升而在植被上部向前运动，但仍然保持开闸式异重流典型形态.由图6(b)可见，根据10张照片的平均结果描述异重流0.1 s内的平均速度和涡度场，涡度

ω=∂ux/∂y-∂uy/∂x

(9)

式中：x和y为水平和垂直方向；ux和uy为水平和垂直方向的速度.

在异重流到达植被之前，速度场和涡度场分布与文献[20]结果一致，近似以最大流速为界，下部涡度值为负值，上部涡度值为正值(涡度正负代表方向：以顺时针为正，逆时针为负).下部涡度负值是由底部无滑移边界条件和底部摩擦力[17]共同引起的，上部涡度正值是K-H不稳定性和斜压不稳定性[3](密度和压力梯度不平行)共同作用的结果.异重流流过植被时，植被顶部区域出现负涡度带，原因在于植被存在阻挡效应，植被顶部和异重流前方迎流面附近的流体以植被顶部为基础形成新的“底部边界”，代替了水槽底部对异重流运动的影响，而异重流在新的“底部边界”上运动形成明显的负涡度带.由于植被的阻挡效应，未能获得异重流在植被内部的涡度场和速度场.

为了进一步分析异重流流入植被时速度v和ω的变化情况，以植被群起点的左侧0.2 m处设为零点(X=0)，分别选取在X=0.15，0.20，0.25 m处选取3个断面(S1, S2, S3)，如图6(a)所示，得到速度和涡度分布情况.由图7(a)可知，在t=3 s时，分析3个断面在x方向上的速度：S1位于植被区域，植被内部速度场由于实验限制未获得呈现速度为0，而异重流最大速度出现在其高度的1/2位置处；S2取于植被起始位置，速度剖面呈现“双峰状”，最大速度与植被顶部的距离约为该断面处异重流高度的1/3，进一步验证了异重流以植被顶部为“底部边界”的运动形式；S3取自植被外部区域，所得到的速度剖面与文献[21]在无植被情况下的研究结果一致.图7(b)为S2于不同时刻的x方向速度，其最大速度值及高度随时间变化不显著，v≈0.065 m/s.对于H<0.05 m区域，异重流断面速度值随时间逐渐增大；对于H>0.05 m区域，断面速度值随时间先增大后减小.涡度变化如图7(c)所示，3个断面的涡度值均小于41/s，断面1和断面2的涡度值分布形态均呈现“双峰状”，且近似于下1/3区域为负，上2/3区域为正；断面3的涡度值则近似于下2/3区域为负，上1/3区域为正.对于图7(d)，t=1, 2, 3 s 时均大致呈现下部涡度值为负，上部涡度值为正的现象；下部涡度值随时间变化显著，上部涡度值变化不明显.

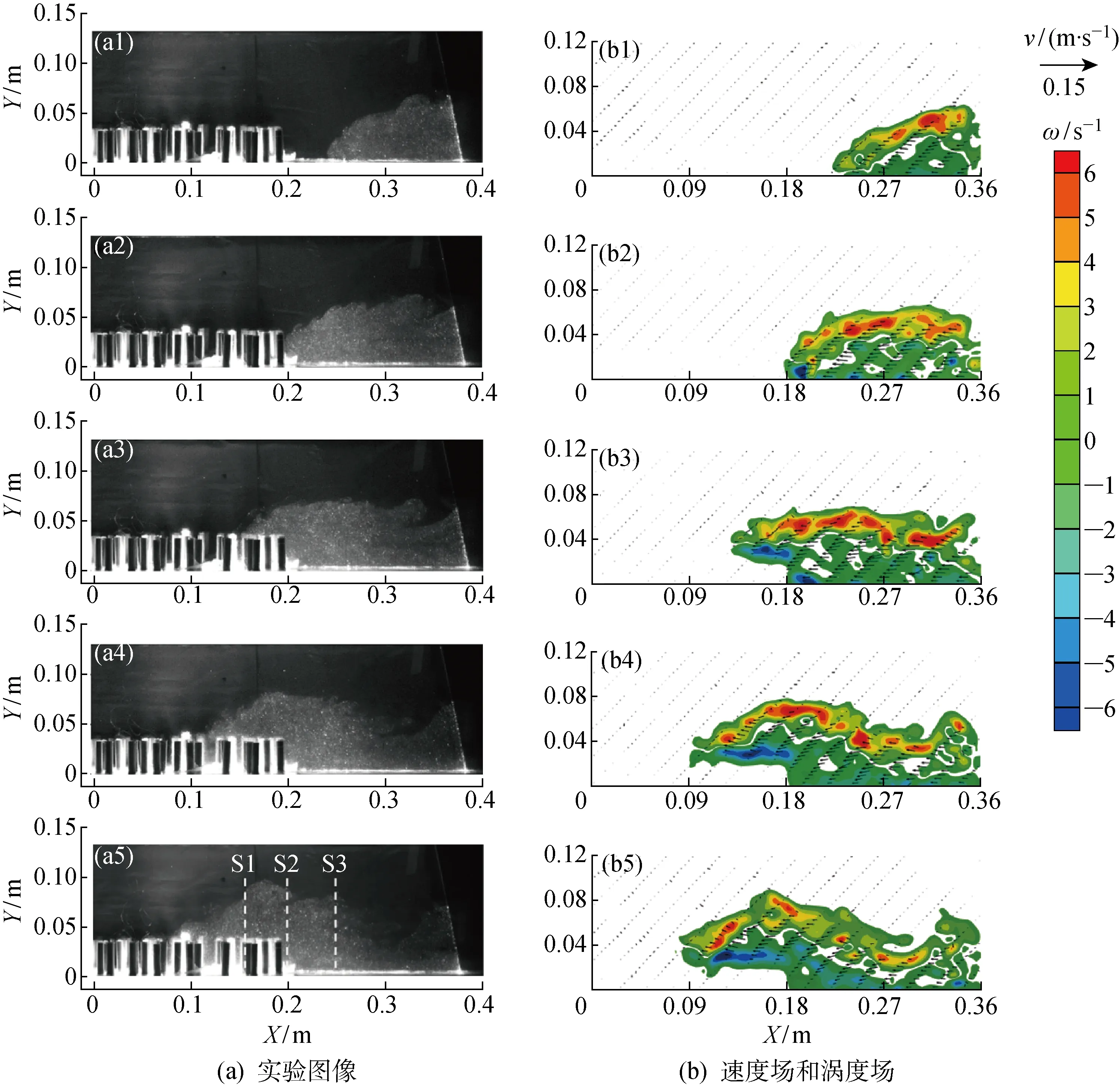
图6 异重流流入植被过程(工况3)

图7 异重流流入植被的动力特征

分析植被密度对异重流涡度场的影响，表4中列出了4种不同工况下异重流上层正向涡度值之和随时间变化的情况，ωave为4个时刻的平均正向涡度，N3为各工况平均正向涡度与工况1平均正向涡度的比值.对于无植被工况，异重流正向涡度在实验研究的时间范围内随时间递增，但增长率逐渐减小.对于有植被工况，工况2中异重流正向涡度与时间成正相关，但增长率逐渐减小，工况3和4中异重流正向涡度随时间呈现先增大后减小的变化规律.这是因为植被密度较小时(RSPF=4.5%)，异重流受植被阻挡效应较弱，在实验时间范围内异重流均处于发展阶段；当植被密度较大时(RSPF=9.0%，18.0%)，异重流形态发展在t=3 s时刻受植被显著抑制而导致正向涡度值呈现减小趋势.对于不同工况，异重流运动时间相同时，植被密度越大，平均正向涡度值越小；植被密度越大，阻挡效应越显著，异重流头部速度越小，掺混作用越弱，抑制正向涡度的发展效果越显著.

表4 不同工况下异重流上层正向涡度值总和

4 结语

在异重流发展过程中，植被会对其运动特性产生显著影响.本文进行一系列开闸式异重流水槽实验，分析短植被群的不同植被密度和高度对异重流运动的影响，主要结论如下：

(1)hv=0.21时，异重流流入植被时会被抬升，而后坍塌并继续保持头部典型形态向前运动；RSPF=9.0%，18.0%，hv≥0.46，异重流流经植被头部典型形态消失，与环境水体界面趋于平滑，最终演化为三角形轮廓，并且头部角度随位置先增加而后递减.

(2)异重流运动过程分为滑塌和自相似阶段，植被不影响滑塌阶段异重流的头部速度，但可使转换点位置前移.当植被高度相同时，植被密度越大，对异重流的阻挡效应越显著；当RSPF=4.5%，9.0%时，植被高度变化对异重流的阻挡效应影响不显著；当RSPF=18.0%时，植被高度越大，对异重流的阻挡效应越显著.

(3)异重流掺混速率在坍塌阶段初期与头部速度关系不显著，但在自相似阶段随头部速度递减，并且植被可以减小掺混速率.掺混系数在流入植被前处于较高值(E≈0.15)，随头部位置迅速递减，流入植被后逐渐递减，流出植被后趋于0且变化不显著.掺混系数与植被密度成负相关，与高度亦成负相关.

(4)异重流在流入植被之前，上部涡度正值是由于异重流与环境水体界面K-H不稳定性和斜压不稳定(密度梯度与压力梯度不平行)的共同作用；下部涡度负值是由于壁面无滑移条件、黏滞阻力导致R-T不稳定性的共同作用.流入植被后，异重流以植被顶部为新的“底部边界”形成负涡度带，但植被会抑制正涡度的形成，且抑制程度与植被密度成正相关.

本研究仅局限于一种异重流浓度且植被长度为短植被群，多种浓度和多种植被长度的研究有待进一步开展，以便将来能更为广泛地应用于实际工程.