考虑裁切效应飞艇囊体模型充气数值模拟与试验

2020-04-08陈务军高成军王雪明

上海交通大学学报 2020年3期

李意，陈务军，高成军，王雪明，何巍

(1.上海交通大学空间结构研究中心，上海 200240；2.中国特种飞行器研究所，湖北荆门 448035)

平流层飞艇作为近地空间多功能作业平台，主要用于通信中继、高空侦探以及科研探索等领域.近年来，随着太阳能电池和新型复合材料等技术的发展，飞艇技术的研究受到越来越多的关注[1-2].飞艇作为一种典型的充气膜结构，在材料层次和结构层次均具有明显的非线性特征.另外，在飞艇的制作过程中，裁片裁切和热合集成对飞艇囊体的初始形态产生一定的影响[3].由于柔性结构准确验证具有一定难度，所以目前关于飞艇囊体精细模型力学性能测试的报道较为少见.

飞艇囊体材料通常为多功能编织的复合材料薄膜，由于纤维织物具有复杂的微观结构且编织结构具有方向性，所以囊体材料表现出较强的力学非线性和各向异性.在正常情况下，囊体基本处于双向受力状态，单轴拉伸试验难以准确地反映囊体材料的力学特性，因此目前常采用双轴试验对其力学特性进行测试.有关膜材料双轴拉伸力学特性的研究表明[4-8]，膜材的双向受力性能具有明显的非线性，且弹性参数受到不同应力比和应力组合的影响.Minami[9]提出多步线性法近似描述纤维材料的力学特性，并采用四边形和三角形单元建立材料的双轴拉伸特征曲面；Bridgens等[10]提出了采用样条曲线方程描述织物纤维材料应力响应面的方法；陈建稳等[5]对URETEK3216LV进行了一系列双轴拉伸试验，得到应力空间中材料弹性参数的响应曲面，并总结应力比和应力组合对膜材双向拉伸力学性能的作用规律.

飞艇囊体常为低阻型双轴椭球体，由纺锤形裁片热合拼接而成.制作过程中裁切及热合对于囊体的初始形状产生明显的影响[11-12]，该效应在结构分析和设计中被称为“裁切效应”.在大体积飞艇的整体设计中，由于裁片数量较多，单幅裁片的横向曲率较小，所以裁切效应通常被忽略[13-14]；对于小型的试验性飞艇模型，裁切效应则会显著影响囊体的初始状态.目前，关于飞艇囊体裁切效应的研究较少，Wagner[12]在各向同性飞艇囊体的分析设计中考虑了裁切效应.

为研究柔性飞艇囊体模型充气过程中的力学响应，本文提出了考虑裁切效应的囊体精细化建模分析方法.首先进行多组应力比下囊体材料双轴拉伸试验，拟合出材料弹性参数应力响应面并编写材料模型子程序；之后对裁片进行建模分析，得到飞艇囊体初始构型的有限元模型，并对囊体充气过程进行数值模拟；最后进行了柔性飞艇模型充气试验，通过对比试验和数值模拟结果，验证了基于裁切效应建模分析方法的正确性.

1 双轴拉伸试验

1.1 囊体材料及试件

飞艇蒙皮一般选择轻质、高强和高模量的膜材，验证性模型尺度通常较小.为便于制作且考虑到飞艇较大的变形，囊体材料采用柔性较好的聚酯薄膜，膜材厚度为0.59 mm，面密度为440 g/m2.

双轴拉伸试验采用十字形切缝试件，试件的对称轴分别平行于织物的经向和纬向，如图1所示.十字形试件臂长为200 mm，中心区域为160 mm×160 mm，夹持区的宽度为40 mm.为了减小应力集中，两臂相交处为半径15 mm的倒角，另外试件臂上设置长度100 mm的平行切缝，用于减小应力松弛，使得中间核心区应力场均匀分布[15].引伸计放置在距离中心点20 mm处，两针脚之间距离为40 mm，用于测量拉伸过程中的材料变形.

1.2 试验过程

基于单轴拉伸试验测量得到膜材经向和纬向强度分别为68.1和53.8 kN/m.参考飞艇结构设计规范FAA-P-8110-2[16]，双轴拉伸试验荷载最大值取材料单轴拉伸强度的25%，试验过程中经向和纬向荷载最大值均取10 kN/m.为考察不同应力比组合方式下膜材的力学特性，双轴拉伸试验选取了11组不同应力比的组合方式，每组循环加载3次，并在组间增加一组1∶1的过渡试验，用于消除前一加载比例的影响.

1.3 试验结果及分析

双轴拉伸试验结果如图2所示，图中σ为应力，ε为应变，图中比例为经向与纬向的应力比，比例之后的“经向”和“纬向”意为该应力比加载下经向和纬向的应力应变曲线.可以看出，在相同的应力水平下，纬向应变明显高于经向应变，并且由于材料各向异性特征明显，在同一应力水平下，经纬向滞回环存在较大差异.观察3次循环过程可知，首次循环应力应变曲线的非线性最为明显.随着循环次数增加，膜材的残余应变逐渐减小，应力应变滞回环趋于稳定.

为了表征材料双轴拉伸力学特性，采用应变响应曲面对材料在应力空间中的响应进行描述.在此基础上可以求解膜材弹性参数响应曲面，求解过程见文献[5]和[7].为了将弹性参数响应面运用到数值模拟中，采用MATLAB对3维曲面进行拟合，得到响应面的数值表达式.其中经向弹性模量、纬向弹性模量和泊松比的响应面拟合回归系数分别为0.982，0.969以及0.956，响应曲面的数学表达式分别为

(1)

式中：Ex和Ey分别为经向和纬向弹性模量；d为膜材厚度；σx和σy分别表示经向应力和纬向应力；μxy为泊松比.

式(1)近似描述了膜材双向受力时弹性模量及泊松比在应力空间中的响应，可通过用户自定义材料子程序(UMAT)整合到Abaqus中[17]，表征有限元模型材料的力学特性.

2 裁切效应及数值模拟

在膜结构制作过程中，裁切部分主要包括裁片、展平、应力补偿以及裁片热合[18-20].由于初始状态下囊体膜面应力为0，所以可以忽略应力补偿过程.本节主要分析裁切、展平以及裁片热合所引起的飞艇囊体初始构型变化，并在此基础上建立有限元模型，对囊体充气过程进行模拟.

2.1 裁切与展平

飞艇囊体设计模型的外轮廓线为双轴椭圆，其形状为绕中心轴的理想回转体，如图3所示.图3(a)中方程分别为囊体左半侧和右半侧的外轮廓线方程.在囊体制作时，根据设计形状沿母线裁切成6幅裁片，每幅裁片大小相同，沿囊体轴向中心对称.取一幅裁片展平，关于膜面展平过程中产生的褶皱问题和解决方法已经有了较多的研究[21-22]，本文基于等面积原则进行展平，为了避免扭曲和皱纹，裁片在纵向进行延长，展平后的裁片如图3(c)所示.

图3 囊体缩比模型及裁片

图4 裁片边界条件

2.2 热合集成

展平后裁片之间通过热合焊接成封闭的整体.由于热合集成过程较为复杂，为了对其进行模拟，可忽略焊接时的细节，简化为平面裁片提升至3维空间的过程.

采用Abaqus对平面裁片提升过程进行模拟.建立平面裁片有限元模型，裁片厚度取0.59 mm，采用壳单元S4R，考虑模型几何非线性，材料属性根据式(1)编写用户自定义材料子程序(UMAT)导入模型中[17].如图4所示，创建裁片边界条件，在裁片周围施加位移边界条件，将裁片边缘上的节点提升至理想模型母线上的对应节点.横切面S截取的裁片展平位置和提升位置如图5所示，图中N为边缘节点，N′为提升后对应的边缘节点，dy，dz为节点提升过程中的位移，方向与图4坐标方向对应.提升后形成的圆弧圆心角为60°.

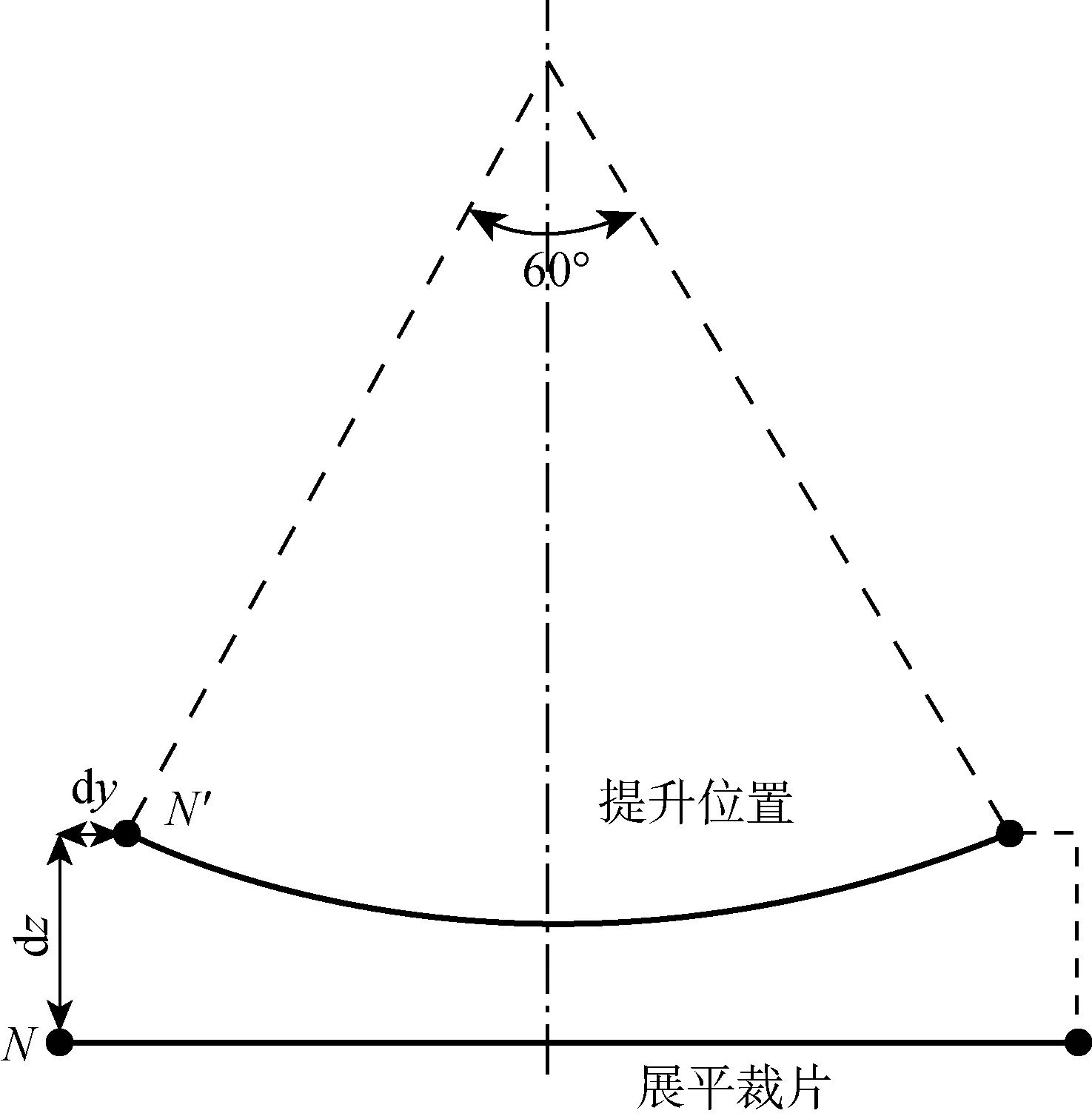
图5 裁片提升示意图

图6 裁片提升过程结束时的竖向位移

模拟得到裁片提升后的变形如图6所示，图中U为竖向位移，为了得到热合集成后囊体初始构型的有限元模型，对提升后的裁片进行轴向阵列，并将裁片之间的节点合并.释放边界条件后生成的有限元模型如图7(a)所示，图7(b)为理想回转体模型，通过对比可知，裁切效应对于囊体初始构型产生明显的影响.

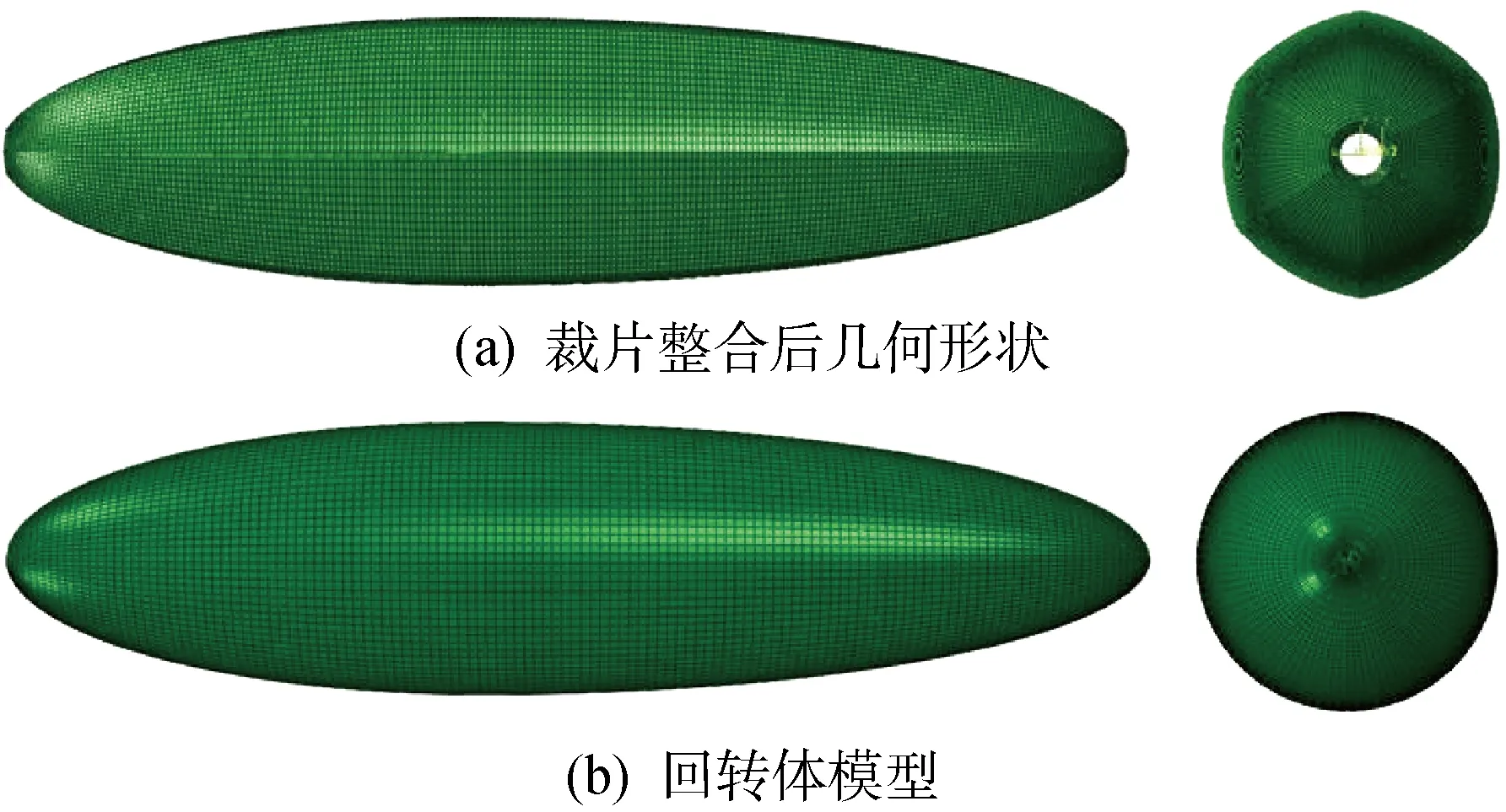
图7 缩尺模型初始构型

2.3 充气过程数值模拟

根据考虑裁切效应得到的囊体初始构型的有限元模型，模拟内压值分别为1，3，5，7，9 kPa时囊体膜面的变形响应.囊体模型采用两点悬挂的约束方式，其材料属性和单元属性均与裁片有限元模型一致.为考察裁切效应的引入对有限元分析结果的影响，建立理想回转体有限元模型，并在相同气压工况、约束形式及材料属性条件下，模拟其充气过程中膜面变形响应.

3 充气试验

3.1 囊体模型

试验对象为柔性囊体模型，囊体长为2.5 m，长细比为4∶1，通过6幅相同裁片沿纵向热合焊接而成.模型头部沿母线热合一条密封拉链，可以沿拉链拉开囊体，实物模型如图8所示.沿囊体拉链所在母线上布置两个吊点S1和S2，吊点S1距离囊体头部0.6 m，吊点S2与S1之间相距1.25 m，模型的几何尺寸及吊点布置如图9所示.囊体材料采用柔性较好的聚酯薄膜，厚度为0.59 mm，与双轴拉伸试验试件的材料相同.

图8 飞艇囊体实物模型

图9 模型吊点分布(m)

3.2 试验过程

充气试验采用气压控制系统调节囊体内压，并测量内压值从0升高到9 kPa的膜面形态变化.由于内压值为0时囊体形状不稳定，将内压值为0.5 kPa作为初始状态.充气过程包括5个内压工况，分别为1，3，5，7，9 kPa.

试验布置如图10所示，采用3维摄影技术对膜面变形进行测量[23].在模型正前方一幅裁片表面贴上反光靶点，靶点呈阵列排布，横向间距为7.5 cm，竖向间距为5 cm.由于充气过程中变形主要发生在膜面中部，将靶点布置在变形较大的中部区域.

图10 充气试验布置

试验对每个气压状态下的膜面形状进行测量，利用单反相机从3个角度拍摄膜面贴有靶点区域，利用Photomodeler Scanner软件对照片进行处理，得到靶点的3维空间坐标.对比初始状态下靶点空间位置，得到靶点区域的变形云图，处理流程如图11所示.

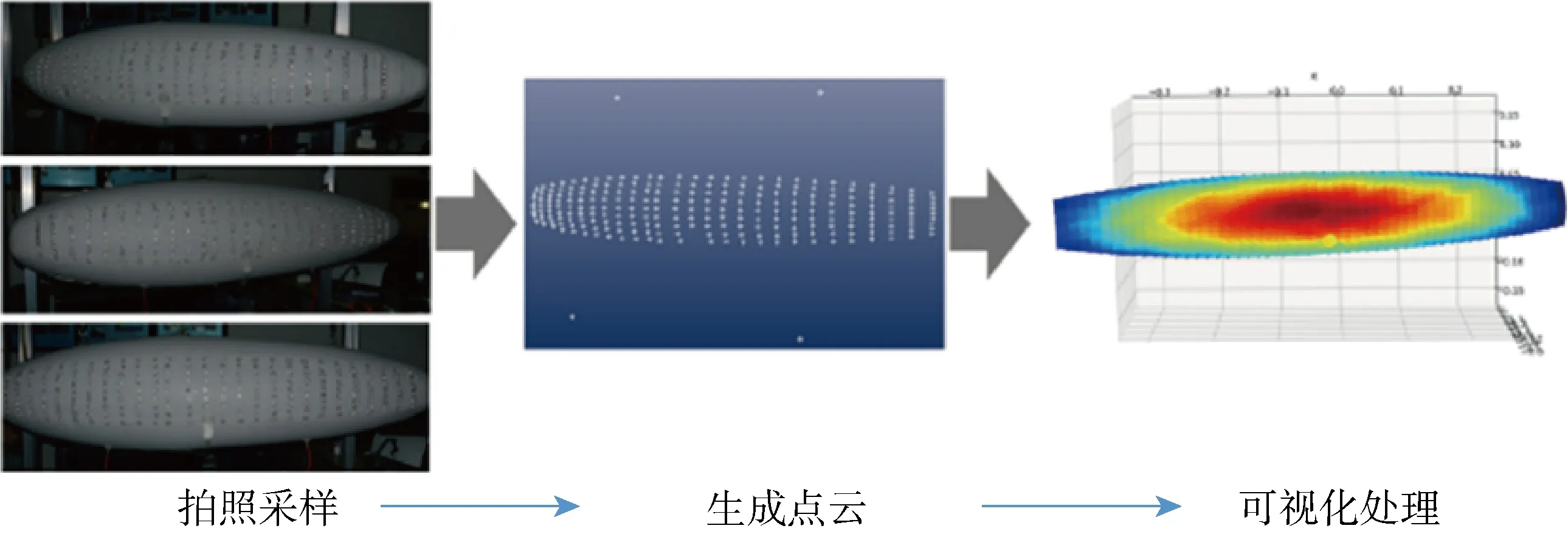
图11 三维摄影处理过程

4 结果与分析

内压为9 kPa时飞艇囊体缩尺模型的数值模拟和试验结果如图12所示，图中SL1为囊体截面半径最大面所在位置，SL2为囊体中间位置截面所在位置.图12(a)为考虑裁切效应的模型变形云图，囊体裁片中间区域的变形大于两侧变形，在垂直于囊体轴向截面内，越靠近裁片拼接的热合缝区域，膜面变形越小.图12(b)为理想回转体模型变形云图，图中显示膜面变形沿囊体轴向出现明显的分层现象，囊体表面变形最大值位于囊体横截面直径最大处.图12(c)为裁片实测的变形云图，可以看出裁片表面变形最大值分布在中间椭圆形核心区域内，越靠近裁片外侧，膜面的变形越小.

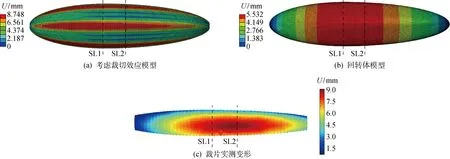
图12 9 kPa状态膜面变形分布对比

对比两种模型数值结果和试验结果可知，考虑裁切效应模型数值结果与充气试验膜面变形分布一致，靠近热合缝区域变形低于裁片中间区域变形，这是由于初始状态下囊体横截面并非理想圆形，而近似为六边形，充气过程中裁片中间区域向外鼓出，热合缝处受到表面张力的影响有回缩的趋势，所以越靠近热合缝处，膜面变形越小.

为了比较充气过程中裁片横截面曲线的变化，分别提取初始状态和9 kPa状态下有限元模型和试验结果的裁片横截面曲线分析，提取充气前、后SL1和SL2处截面曲线变化，如图13所示，图中p为内压，横坐标x为裁片横截面(SL1,SL2)弦长方向坐标，设弦长中点为0，纵坐标y为裁片横截面曲线.可见，考虑裁切效应模型裁片截面曲线与试验曲线基本一致，初始状态下，试验模型与考虑裁切模型裁片截面曲率大致相同，均小于回转体模型裁片曲率；随着气压的增加，试验模型与裁切模型截面曲率增大，逐渐接近回转体模型，说明囊体充气前后由初始近似六边形演变成圆形，证实了基于裁切效应的建立的初始构型有限元模型的正确性.

图13 SL1和SL2处裁片截面曲线有限元和试验对比

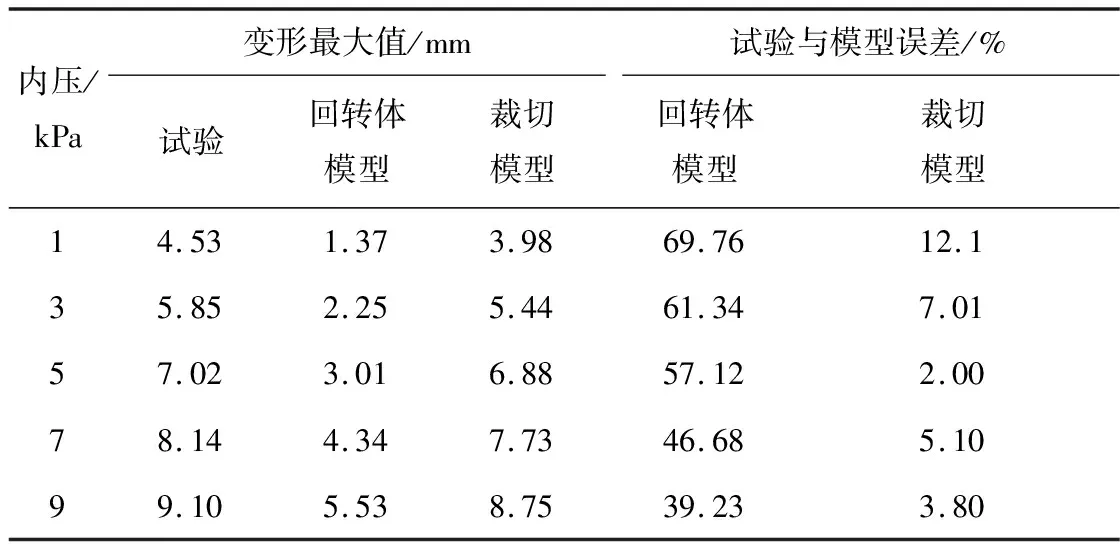
表1所示为不同内压工况下飞艇囊体数值模拟和试验结果中膜面变形最大值对比.可见，回转体模型分析结果中膜面变形最大值误差为40%～70%，主要原因在于回转体模型对于初始状态下囊体横截面假设不正确，所以充气过程中横截面并非均匀地向外扩张.考虑裁切效应模型膜面变形最大值的变化趋势与试验结果基本一致，当内压为1 kPa时，裁切模型的误差为12.1%，并且随着内压的增大，模型的误差逐渐减小，这是由于内部气压比较低时，囊体的刚度比较小，形态不稳定，试验模型的初始状态与有限元模型的初始状态存在偏差，数值模拟的结果误差较大；当内压增大时，囊体形态逐渐稳定，裁切模型和试验模型在高应力状态下变形基本一致，数值模拟误差逐渐减小.

表1 不同内压下试验与数值模拟变形最大值及误差

Tab.1 Maximum deformation and error of test and numerical simulation in different internal pressures

内压/kPa变形最大值/mm试验回转体模型裁切模型试验与模型误差/%回转体模型裁切模型14.531.373.9869.7612.135.852.255.4461.347.0157.023.016.8857.122.0078.144.347.7346.685.1099.105.538.7539.233.80