气动伺服弹性系统的自适应陷波器算法设计

王雨，崔茅，张公平，唐炜，＊

1.西北工业大学，陕西 西安 710129

2.中国空空导弹研究院，河南 洛阳 471009

3.航空制导武器航空科技重点实验室，河南 洛阳 471009

随着空中目标性能的不断提高，空空导弹的发展对射程、速度和机动性能提出了更高的要求，同时为适应四代机舱内高密度挂载的需求，新一代空空导弹外形设计趋于细长化[1]。有研究表明，当导弹长细比大于15时，其弹体的弹性特性凸显，且会对飞行安全造成负面影响[2]。这是因为大长细比空空导弹的刚度降低，其弯曲振动频率也随之降低，在其发射和飞行过程中，弹体易受到推力及气动力的影响而发生弹性振动。由于导弹的陀螺仪、加速度计等测量单元直接安装在弹体上，弹体的弹性振动信号将经这些测量单元被引入控制回路，造成自动驾驶仪的控制信号产生额外输出，进而导致伺服单元响应后进一步加剧弹性振动，严重时甚至会造成系统失稳，姿态或加速度跟踪控制发散，引起弹体结构破坏[3]。

针对这一问题，George[4]将导弹的弹性模态看作一种未建模不确定性来设计鲁棒控制器，实现对弹性信号抗扰动的姿态控制。然而鲁棒控制器设计过程较为复杂，控制器阶次一般较高，且控制性能对模型具有一定的依赖性。朱敬举等[5]的研究表明，使用二阶固定极点式陷波器可以有效消除导弹固定频率的弹性振动信号对控制回路的影响。然而，我们知道在导弹的飞行过程中，随着其所携带的燃料的不断燃烧，弹体的整体质量和刚度分布将不断降低，造成弹性振动频率不断下降，传统的固定极点式陷波滤波器无法满足在导弹的整个飞行过程中对弹性振动信号进行滤除。因此，迫切需要设计一种陷波中心频率能够随振动频率实时改变的自适应陷波器，对飞行中导弹的振动信号进行滤除，以保证控制系统的准确性和稳定性。Choong‐seok[6]基于Guass‐Newton算法对运载火箭的多阶弹性模态进行估计，取得了理想的效果，但这种方法只适用于模态频率变化缓慢的情况。陈光山等[7]利用消除记忆最小二乘法在线辨识弹性模态频率，实现了对弹性振动信号的自适应滤波，但该方法对弹性振动频率的辨识精度不高，不利于陷波器的设计。

本文利用最小均方（least Mean Square,LMS）算法对测量反馈信号进行迭代运算，实时估计弹性振动频率，并将此估计频率作为二阶ⅠⅠR数字陷波器的陷波中心频率的实时更新。仿真结果表明，设计的自适应陷波器能够准确估计振动信号频率并将其滤除，克服了固定极点式陷波器的缺点，保证了三回路自动驾驶仪对过载的准确跟踪。

1 弹性导弹数学模型

由理论和实践均可知，弹性导弹的一阶弯曲振动模态对其气动伺服弹性稳定性的影响最大[5]。因此，考虑弹性导弹在纵向方向上的刚体平动、刚体转动和弹体一阶弯曲振动的弹性导弹运动方程可表示为：

式中：q为广义坐标矩阵；q1，q2，q3分别为刚体平动、刚体转动和一阶弯曲运动的广义坐标；M为广义质量矩阵；m1，m2，m3分别为弹体质量、弹体转动惯量、一阶弯曲振动的广义质量；K为广义刚度矩阵；Q为广义气动力矩阵。

由于弹体的弹性特性，因此，考虑弹体弯曲振动引起的非定常气动力，这里主要考虑由弹体产生的广义非定常气动力Qα和由舵面产生的广义非定常气动力Qd，即：

Q=Qα+Qd（2)

本文采用气动导数法计算广义非定常气动力。基于定常流动的计算公式，假设弹体局部迎角α等于合成速度矢量与弹体纵向轴线之间的瞬时夹角，则此单位长度弹体的升力为：

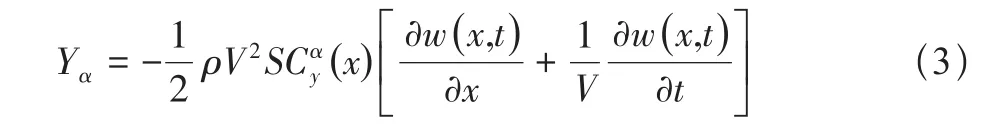
式中：ρ为大气密度；V为导弹飞行速度；S为气动参考面积；(x)为弹体任一点x处关于迎角的升力系数导数；w(x,t)为弹体任一点x处的纵向位移。

同理，舵面压心处的升力为：

式中：xe为舵面压心的位置；为舵面压心处关于迎角的升力系数；为舵面压心处关于舵偏δ的升力系数；wd(xe,t)为舵面压心的纵向位移。

本文将弹体沿弹体纵向轴线看作一段，则有：

式中：f1(x)，f2(x)，f3(x)分别为刚体平动、转动、一阶弯曲振动的模态振型；x1为全弹弹体压心位置；xr为舵面转动轴的位置。

根据广义力的定义，有：

2 弹性振动信号频率的估计与跟踪

2.1 频率估计

考虑如下二阶无限脉冲响应（ⅠⅠR）陷波器[6]：

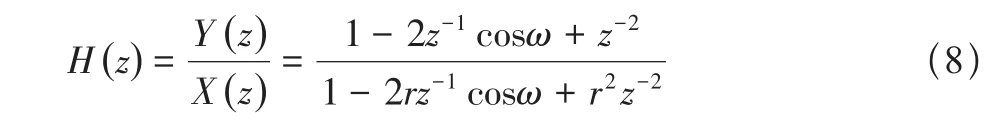
式中：ω=2πf/fs为陷波角频率，f为陷波频率，fs为采样频率，参数r决定陷波器带宽。

由于上述陷波器的零点位于z平面单位圆上，因此其陷波深度为无限深。

考虑一组叠加了一阶弹性振动信号的导弹姿态测量信号x(n)，如果忽略噪声的影响，一旦陷波器的陷波频率ω收敛到一阶弹性振动信号的角频率ω0（ω0=2πf0/fs），则这组测量信号通过该陷波滤波器后的输出y(n)≈0，即将测量信号通过不同陷波角频率（在区间[0,π]上取）的陷波滤波器，陷波器的输出的最小功率处所对应的ω即为估计的振动信号角频率。为此，引入均方误差（Mean Square Error,MSE）函数[7]：

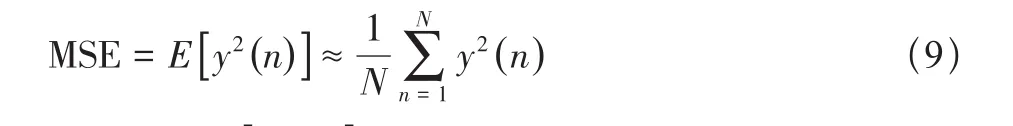
通过求得E[y2(n)]在区间[0,π]上的极小值所对应的角频率，即可获得所估计的振动频率。区间[0,π]取的间隙越小，则最后估计的振动频率越准确。

图1展示了一个使用该算法进行频率估计的例子：取一组振动信号频率为90Hz、采样频率为1024Hz、信噪比为-20dB的测量信号的40个采样数据，将[0,π]等分为50个点，取陷波器参数r=0.95。均方误差函数在ω=0.577rad（f=91.84Hz）处取得极小值，因此，根据该组测量数据所估计的振动信号频率为91.84Hz。

图1 均方误差函数随角频率的变化Fig.1 Mean square error function varying with radians

式中：μ为LMS算法收敛步长，且μ应当是一个很小的值（μ≪1）以保证算法的收敛性。

在振动信号的精确角频率处，MSE函数具有最大的偏差率，因此，利用LMS算法，不精确的角频率初值最终将收敛至MSE函数的全局最小值。

2.2 频率跟踪

导弹的弹性振动频率初值ω0可以通过2.1节中的频率估计算法进行估计，也可以由地面测试获得，并且该初值将用于下面的频率跟踪。

获得导弹不精确的振动频率初值以后，我们使用基于最小均方Least Mean Square（LMS）算法的角频率迭代获得期望的振动频率精确值。取式（9）的导数，并令其为零，可以得到：

其中，β(n)为梯度项，定义为：

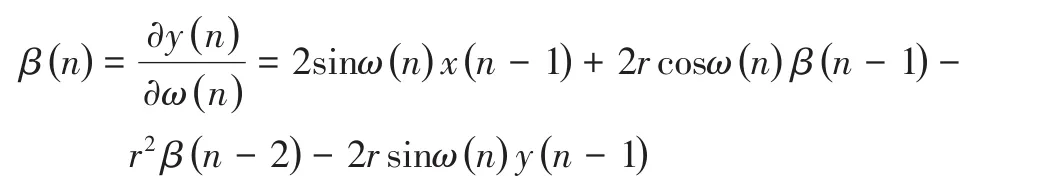
3 控制系统设计

导弹姿态/过载控制系统的作用是在导弹飞行过程中实现导弹过载/姿态的快速与稳定跟踪，并实现闭环系统一定的鲁棒性能。传统的导弹控制系统一般是基于导弹的刚体模型进行设计，而忽视了弹性振动的影响。在工程上，一般根据弹性振动频率设计陷波滤波器将振动信号滤除，避免其恶化控制系统的性能。针对弹性导弹的闭环控制系统框图如图2所示。

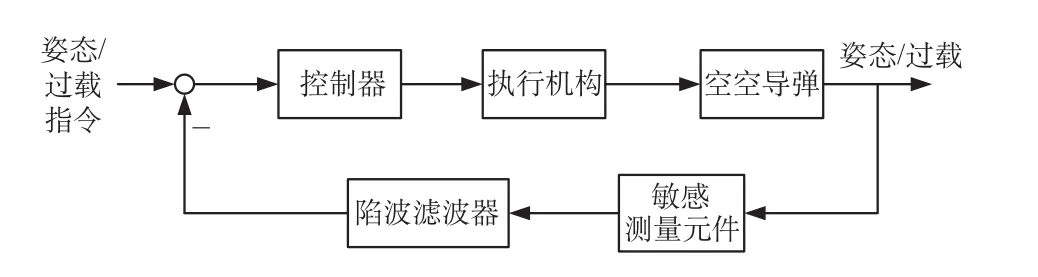
图2 弹性导弹闭环系统框图Fig.2 Flexible missile closed-loop block diagram

3.1 三回路自动驾驶仪设计

三回路自动驾驶仪作为一种经典的空空导弹过载驾驶仪，因其良好的控制性能和鲁棒性，得到了广泛的应用。此外，由于导弹飞行过程中迎角不能直接通过仪表进行测量，需要通过角速率陀螺仪或加速度计的测量信号近似计算得到，为解决近似迎角反馈而给传统三回路自动驾驶仪所带来的静差，伪迎角自动驾驶仪被提出[8]。三回路自动驾驶仪的本质是PⅠ校正网络，其原理主要是在低频处提供较大的增益，使闭环系统的增益趋近于1，消除控制回路的静差。

将第1节所述的弹性导弹数学模型进行的小扰动线性化，推导出刚性导弹和弹性导弹的俯仰运动模型。基于刚性导弹线性模型，我们设计了伪迎角三回路自动驾驶仪，其原理框图如图3所示。

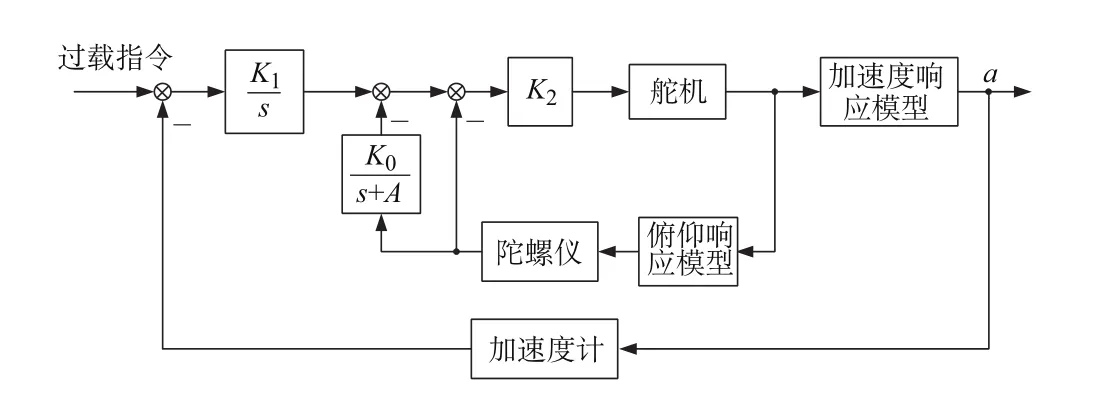
图3 伪迎角三回路驾驶仪原理图Fig.3 Schematic diagram of three-loop autopilot with pseudo attack angle feedback

由图3可知，伪迎角三回路驾驶仪由加速度反馈回路、伪迎角回路、阻尼回路构成。本文中，为保证闭环系统较快的响应速度和一定的鲁棒性，图3中三回路自动驾驶仪的4个参数取值分别为：

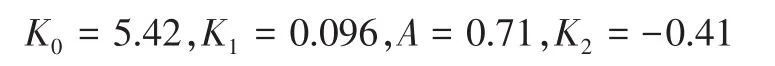
3.2 自适应陷波滤波器设计

传统陷波滤波器可以衰减某一固定频率处振动，削弱弹性结构与伺服机构之间的耦合关系，因而被广泛应用于飞行器气动伺服弹性增稳设计中。但是这种陷波器极点固定，直接应用于空空导弹这类飞行过程中燃料质量、温度会发生较大改变而造成其弹性特性变化的飞行器并不合适。为此，基于本文第2节所述的信号频率的估计与跟踪算法，设计了自适应陷波滤波器，其原理如图4所示。利用加速度计的测量反馈信号，对导弹实时的弹性振动进行频率估计与跟踪，并将该估计频率作为新的陷波器下陷频率。

本文中，滤波器采用式（8）所述的二阶离散陷波滤波器，陷波器带宽参数取值为r=0.999，采样频率为fs=1024Hz，陷波器下陷角频率ω随弹性振动频率估计跟踪算法的实时更新而变化；此外，式（10）所描述的频率跟踪算法的收敛步长取值为μ=0.0001。

图4 自适应陷波滤波器原理Fig.4 Schematic diagram of adaptive notch filter

4 仿真验证

为验证本文所提算法的有效性，本文对仿真做如下假设：设通过地面测试获得的弹性振动信号为f0=25Hz，即将本节所述的固定极点式陷波器的下陷角频率和自适应陷波器的下陷角频率均设置为ω0=0.1534rad。由于导弹飞行过程中燃料的燃烧，导弹质量变轻，造成导弹弯曲振动频率变小。

按照图2所示的连接关系构造仿真，将陷波器串入反馈回路，实现对导弹一阶弯曲振动信号的滤除，防止其被引入控制回路，恶化跟踪控制效果。此外，仿真中舵机的特性利用式（11）的三阶线性模型来描述，即舵机带宽为33.2Hz，并且将舵机的响应幅值和响应速度限制在[-0.35，0.35]和[-5.23，5.23]。仿真中设置的过载指令为20m/s2。

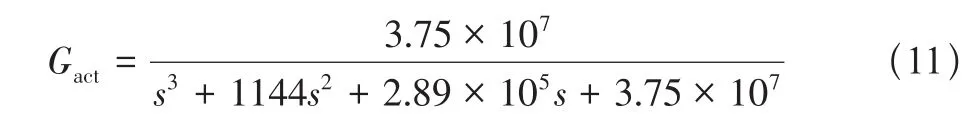
将参数如前述的固定极点式陷波器串入控制回路时，闭环系统的控制性能如图5所示。由于导弹弯曲振动信号降低，根据地面测试数据所设计的固定极点式陷波滤波器的下陷频率与实际导弹振动频率相差较大，固定极点式陷波器失去了其滤除掉振动噪声的作用。振动信息被引入到控制回路，造成控制器输出了额外的控制信号，舵机偏转产生了附加的气动力，从而影响了弹体的气动特性，弹性振动加剧，如此往复，导致了实际的纵向加速度跟踪响应逐渐发散，但由于舵机的物理限制，导致最终的响应在加速度为20m/s2上下进行等幅振荡。

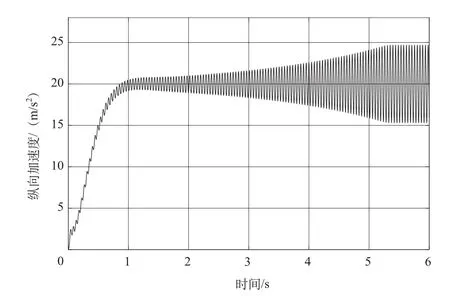
图5 反馈回路串入固定极点式陷波器的控制效果Fig.5 The tracking performance with offline notch filter

将仿真中的固定极点式陷波器换为第3节中所设计的自适应陷波器，此时过载的跟踪控制指令如图6所示，频率跟踪器的实时跟踪情况如图7所示。从图6可以看出，串入自适应陷波器的闭环系统的加速度跟踪效果一开始仍然存在一定程度的抖动，但大约2s后，控制效果趋于平滑，并保持在20m/s2。结合图7分析可得，这是由于刚开始时由于导弹真实振动频率与初始估计频率相差较远，而本文中的频率估计跟踪算法是通过逐次迭代更新来逼近真实振动频率的，该算法大约在1.9s处实现了对导弹振动频率的准确估计，从而根据该频率估计器估计频率设计的自适应陷波器准确地滤除了导弹的振动噪声信号，闭环系统实现了对过载指令的准确跟踪[9-11]。

图6 反馈回路串入自适应陷波器的控制效果Fig.6 The tracking performance with adaptive notch filter

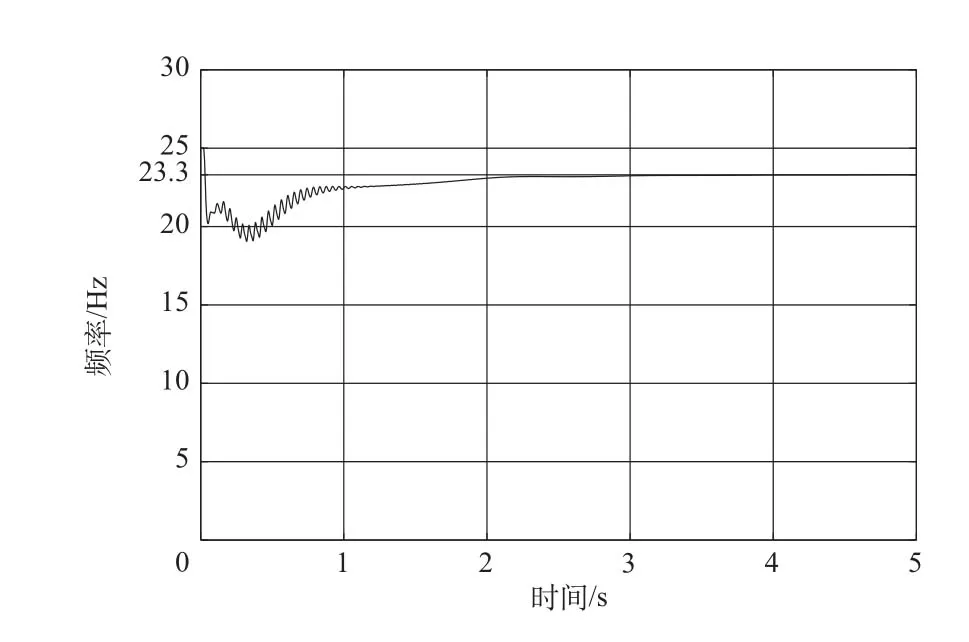
图7 弹性振动频率的跟踪Fig.7 The frequency tracking of the bending vibration

5 结论

本文针对大长细比空空导弹凸显的气动伺服弹性问题设计了一种可行的自适应陷波器，解决了导弹飞行过程中弹性振动变化而造成的固定极点式陷波滤波器失效的问题。基于LMS算法的迭代过程对振动信号频率进行实时估计，并且算法迭代过程中只有一个自适应参数，迭代过程快速且估计频率准确，因此，基于该算法的自适应陷波器在导弹过载跟踪控制中具有很好的仿真效果。