随机子空间颤振模态参数自动辨识方法研究
2020-04-07刘立坤闫轲
刘立坤*,闫轲
中国飞行试验研究院飞机所,陕西 西安 710072
颤振飞行试验是新型或结构重大改型的飞机都必须要经过的试验项目之一,其主要目的是确定飞机在设计包线范围内没有颤振现象的发生并具有足够的颤振裕度。该项试验高风险、高耗费和周期长的特点对信号分析提出了实时、准确的要求。由于颤振飞行试验存在激励力不足、测量点有限、试验环境复杂等特点,通过颤振飞行试验测量得到的试验数据往往具有信噪比低、模态密集、常夹杂谐波分量等特点[1]。工程人员常需要结合地面共振试验结果和个人主观经验剔除虚假模态,筛选出置信度较高、表示物理系统特性的模态参数辨识结果[2]。此外,目前国内颤振飞行试验模态参数辨识仍然以频域方法为主,模态参数辨识精度受限于频谱估计的准确程度。这些因素都会增加模态参数准确、快速辨识的难度,不利于颤振飞行试验过程中实时和准实时分析。
随机子空间方法(SSⅠ)是近年来发展起来的一种运行模态时域分析方法。与传统频域方法相比,该方法直接利用时域数据进行分析,不受频谱估计频率分辨率的影响,能够准确识别系统的模态参数。但基于SSⅠ方法的模态参数识别需要人为地对稳态图进行分析,存在人工分析工作量大、效率低,不能满足颤振飞行试验实时和准实时分析的需求,因此有必要针对颤振飞行试验研究高效准确的模态参数自动辨识方法。近20年来,人们开始逐渐开始关注模态参数自动识别方法的研究。Magalhaes等将分层聚类技术应用到模态参数自动识别方法中[3];姜金辉等提出了正交多项式和多参考点最小二乘复频域识别方法结合FCM(Fuzzy‐C)聚类技术的稳态图自动分析方法[4];汤宝平等提出了基于谱系聚类的SSⅠ自动识别方法[5];最近,郑沛娟等采用图论聚类方法对桥梁结构进行了监测,提出了基于图论聚类方法的模态参数自动辨识方法[6];宋明亮等对模态参数自动识别方法进行了回顾,并在文章最后以SSⅠ模糊聚类方法和频域分解方法结合模态置信准则(MAC)对一钢筋混凝土建筑成功进行了分析[7]。上述方法均能够进行模态参数自动识别,在土木工程等领域有一定的应用。但是基于聚类方法的模态参数自动识别仍存在一定问题,如kmeans聚类需要事先给定聚类数目[8],dbscan等密度聚类方法需要给定聚类领域半径[9],分层聚类需要设定分层树截断规则,非分层的模糊聚类则需要预先设定聚类数目和聚类中心等[10],这些因素都给模态参数自动识别带来了一定的困难。
本文以随机子空间法为基础,针对颤振飞行试验模态分析测量点少、常存在谐波分量的特点,结合扩展模态置信度准则、扩展峰度系数法,提出了一种模态参数自动辨识方法。分别以四自由度弹簧质量系统仿真算例和颤振飞行试验实测数据进行了验证。
1 随机子空间方法简介
假设大气湍激励条件下的n自由度飞机结构时域状态空间模型为:

式中:yk∈Rn×1为第一个测量点k时刻采集的响应信号;xk∈Rn×1为系统的状态矢量,n为系统阶次;A∈ Rn×n为状态矩阵;c∈ Rl×n为输出矩阵;wk∈Rn×1为过程噪声;vk∈Rl×1为测量噪声。
定义输出协方差矩阵Ri=E[yk+i·yTk],其中E表示数学期望。
构造Toeplitz矩阵如下:

将式(2)中Toeplitz矩阵分解得T1|i=OiTi,其中Oi为可观测矩阵,Ti∈Rn×li为扩展可控矩阵。对可观测矩阵Oi进行奇异值分解得:
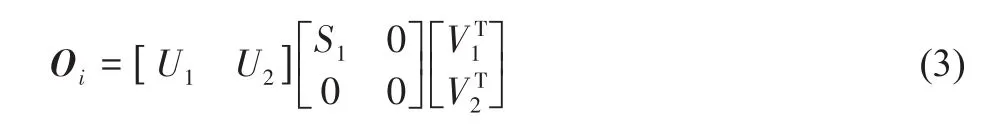
随机子空间方法根据不为零的奇异值个数确定系统阶次,再根据U1、S1计算出系统矩阵、输出矩阵,最终得出系统的模态参数。
2 虚假模态剔除指标
针对颤振飞行试验测量点少、响应信号信噪比低、常夹杂谐波分量等特点,虚假模态剔除指标除传统稳态图中各阶次模态频率误差Δf<1%、阻尼误差Δξ<1%、模态置信准则误差ΔMAC<1%等硬判据外,还增加了扩展模态置信度准则和扩展峰度系数检测法。
2.1 扩展模态置信度准则
扩展模态置信度准则(MACXP)最早由P.Ⅴacher等于2010年提出[11],其将传统模态置信准则扩展至复模态领域,并通过加权方式考虑了极点的影响。MACXP主要用于比较两个模态振型u1、u2之间的相关性,其定义如下:
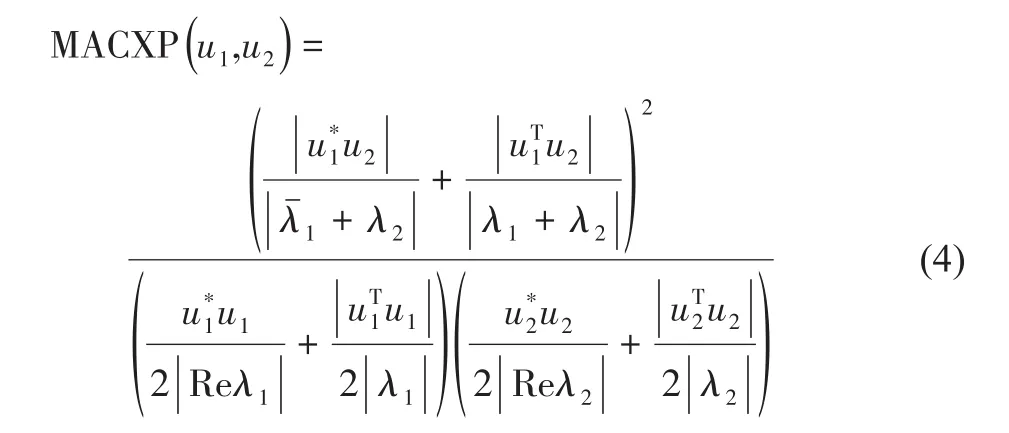
式中:λ1、λ2为对应于振型u1、u2的极点,MACXP ∈ [0,1],MACXP越接近1表明两个模态相关性越高。
2.2 扩展峰度系数检查法
扩展峰度系数法结合随机变量峰度系数的概念,主要用于检测信号中由旋转部件(如飞机螺旋桨发动机)引起的谐波分量。随机变量的峰度系数提供了一种表示概率密度曲线的平缓程度的方法。峰度系数定义为随机变量经均方差标准化后的四阶中心矩:
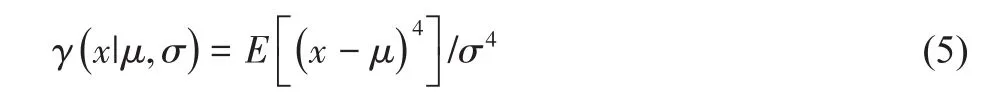
式中:μ为x的平均值;E为期望值。Jacobsen等指出单纯结构模态响应的概率密度函数服从正态分布,其峰度系数γ<3,而谐波分量的峰度系数γ≫3[12]。扩展峰度系数法以此为依据,对飞行颤振试验响应数据中的谐波分量进行剔除。
3 基于SSI的颤振模态参数自动辨识方法
基于SSⅠ的颤振模态参数自动辨识方法,首先采用随机子空间方法识别飞机结构模态参数,利用硬判据指标得出初步稳态图。然后,分别根据扩展模态置信度准则和扩展峰度系数法进一步剔除虚假模态,去除谐波分量的影响。图1为模态参数自动辨识流程。
然后,将剩余计算结果按照频率进行排序,定义模态i,j之间的距离为:
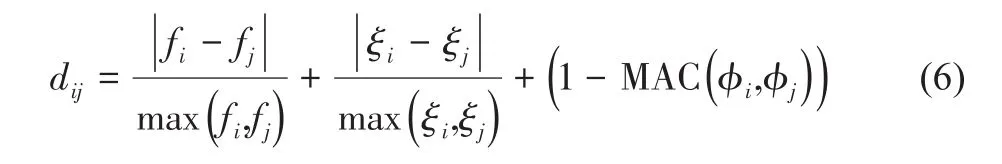
式中:f为模态频率,ξ为模态阻尼比,φ为模态振型。
按照距离稳定曲线拐点对剩余结果进行聚类,如图2所示,图中黑色方块为聚类节点的序号,并以Δf<1%,Δξ<1%,ΔMAC<1%进一步剔除聚类结果中的异常点并去除聚类数目小于5次的结果。
4 实例验证
4.1 仿真试验验证
假设一四自由度弹簧质量系统,其结构如图3所示,4个质量块质量均为10kg,弹簧刚度均为10000N/m,阻尼系数均为10N/ms。在Matlab中采用零均值高斯白噪声对该结构进行激励,设置采样率为50Hz,仿真时间300s,随机子空间辨识阶次为100阶。向响应信号中加入式(7)所示的谐波分量:

式中:fh=20Hz为谐波分量对应的频率。

图1 模态参数自动辨识流程Fig.1 Automatic identification process of modal parameters
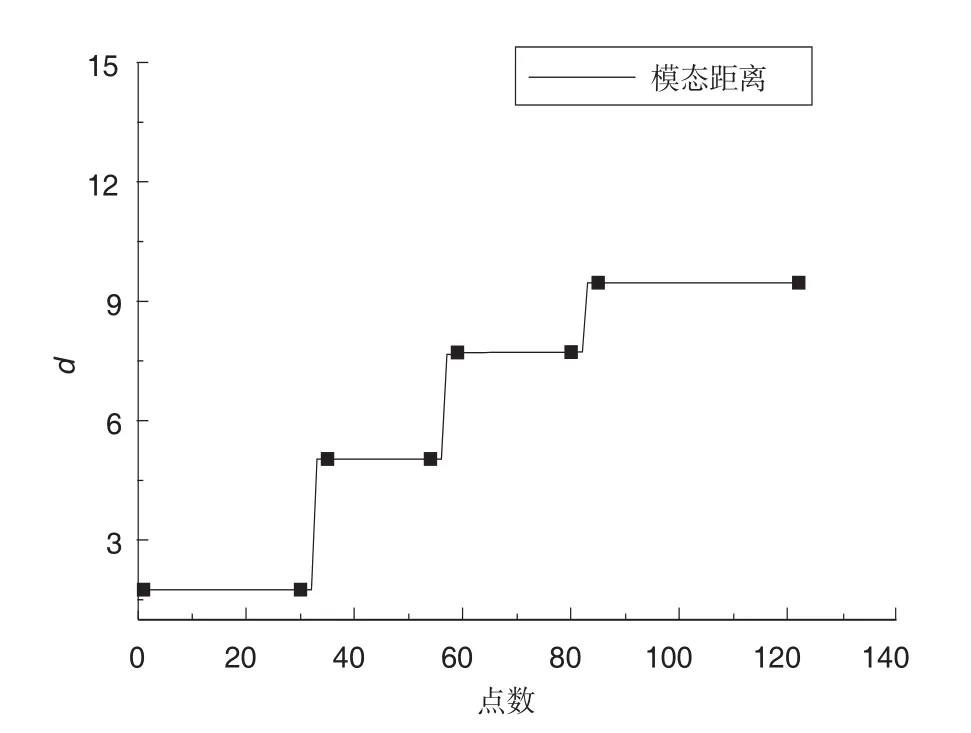
图2 模态间距离稳定曲线Fig.2 Modal distance stability curve

图3 四自由度弹簧质量系统Fig.3 Four degrees of freedom spring-mass system
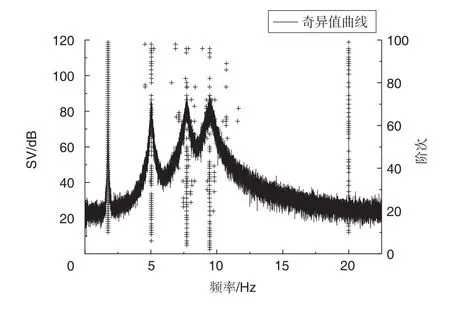
图4 经过硬判据MACXP筛选过的稳态图Fig.4 Stable diagram filtered by hard criteria MACXP
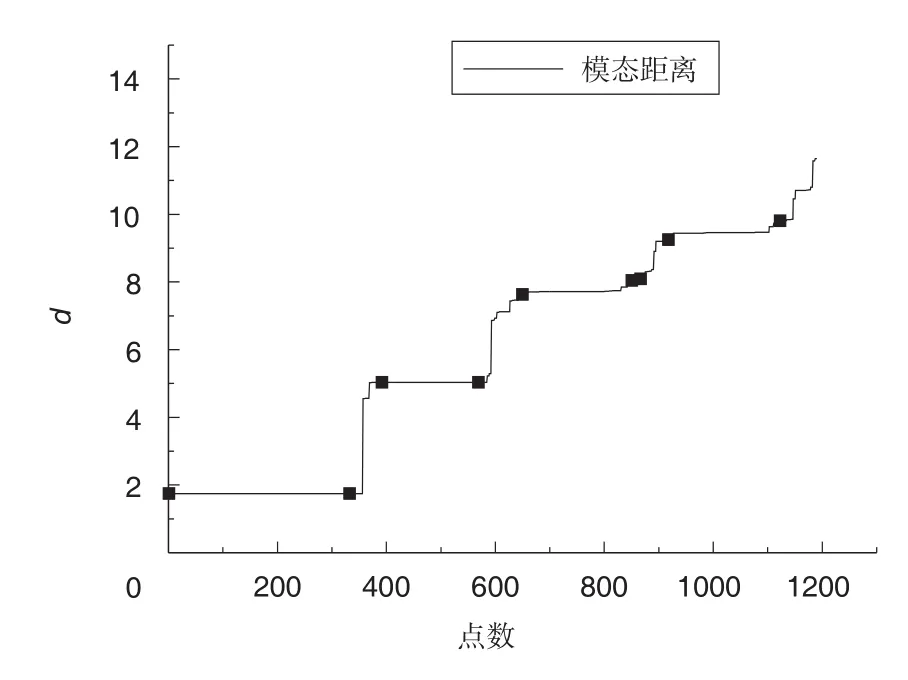
图5 模态间距离稳定曲线Fig.5 Modal distance stability curve
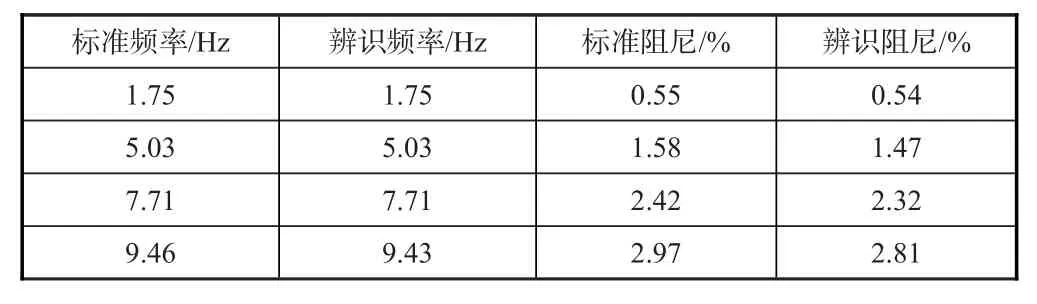
表1 模态参数自动辨识结果Table 1 Automatic identification results of modal parameters
图4~图6分别给出了经过MACXP指标的初步稳态图、距离稳定曲线和经过距离聚类后的稳态图。图中,SⅤ为奇异值。表1给出了模态参数自动辨识结果和真实频率阻尼的比较。
结果表明,MACXP判据由于结合了极点信息,运用该判据所得稳态图较为清晰,能够有效去除虚假模态。结合扩展峰度系数法去除了谐波分量的影响。按照距离稳定曲线进行聚类,进一步剔除了异常点,聚类后的频率和阻尼参数曲线较为稳定,得出的模态参数辨识结果与真实值一致性较好。

图6 去除谐波分量的稳态图Fig.6 Stable diagram after removing harmonic components
4.2 飞行颤振试验验证
某运输类飞机颤振飞行试验,在一高度保持稳定平飞60s,利用大气湍流激励对飞机结构进行激励,使用振动加速度传感器测量机翼、发动机、机身、尾翼等结构振动响应,测试采样率为512Hz,设置抗混叠低通滤波器截止频率为120Hz。表2给出了该飞机地面共振试验主要模态结果。根据设计厂家给出的相关资料,该飞机螺旋桨发动机一阶谐波分量约为36Hz。

表2 某运输类飞机地面共振试验结果Table 2 Ground resonance test results of a transport
选取机翼结构所安装的4个法向加速度传感器,分别使用人工频域分解法和基于密度聚类的SSⅠ自动辨识方法对大气湍流激励所得响应数据进行分析。图7为仅通过硬判据得出的稳态图。图8为模态间距离稳定曲线。图9给出了结合扩展峰度系数法后聚类稳态图。结果表明,扩展峰度系数法能够有效去除螺旋桨发动机引起的36Hz谐波分量,经过距离聚类后所得稳态图较为清晰,有利于工程人员对物理模态进行选取。表3给出了人工频域空间域分解法(FSDD)和SSⅠ模态参数自动辨识方法的结果对比,两种方法所得结果均能满足工程试验需求。两种方法模态参数辨识差异的主要原因是人工FSDD方法辨识精度受谱线估计准确程度、曲线拟合精度等人为因素的影响。
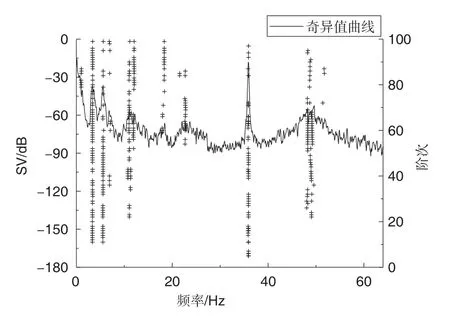
图7 硬判据MACXP筛选后的稳态图Fig.7 Stable diagram filtered by hard criteria MACXP

图8 模态间距离稳定曲线Fig.8 Modal distance stability curve
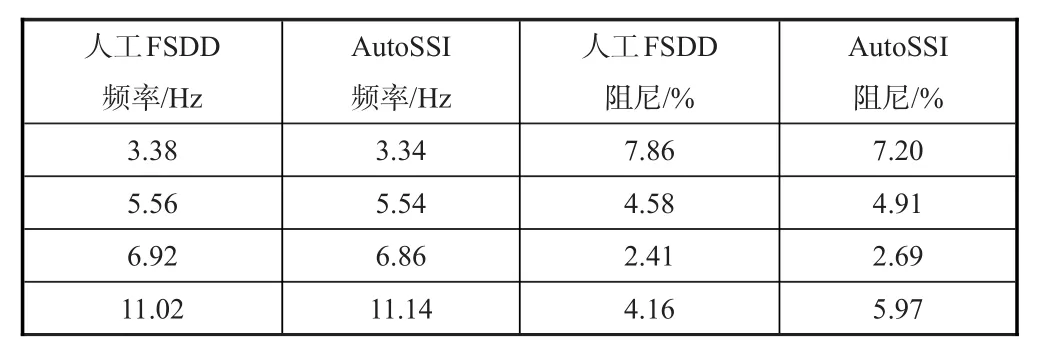
表3 模态参数辨识结果Table 3 Modal parameters identification results
5 结论
通过分析,可以得出以下结论:
(1)以随机子空间方法为基础,结合扩展模态置信度准则和扩展峰度系数法,提出了一种以距离曲线聚类的模态参数自动辨识方法。
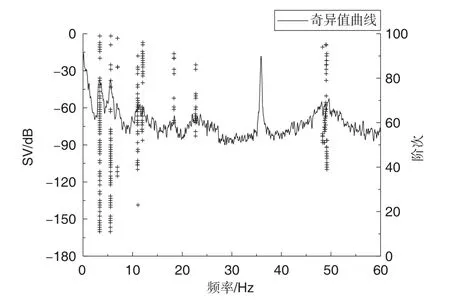
图9 去除谐波分量的稳态图Fig.9 Stable diagram after removing harmonic components
(2)仿真试验和颤振飞行试验结果表明,该方法能够自动识别模态参数,MACXP准则所得稳态图较为清晰,扩展峰度系数法能够有效去除谐波分量的影响。与传统人工模态参数方法相比,其所得模态一致性较好,可用于飞行颤振试验过程中的实时和准实时分析。
