调频式钢轨阻尼器安装偏差对钢轨振动衰减率的影响

李政 杨龙才 周新 赵磊 金浩

（1.同济大学道路与交通工程教育部重点实验室，上海 201804；2.上海市轨道交通结构耐久与系统安全重点实验室，上海 201804；3.中国铁道科学研究院集团有限公司铁道建筑研究所，北京 100081）

为降低城市轨道交通环境振动给居民生活、古建筑和精密仪器等带来的影响，往往采取使用减振扣件、减振轨道等措施［1］。调频式钢轨阻尼器是一种应用于振源处的轨道减振降噪措施，能够显著增加钢轨阻尼，达到减振降噪目的，目前被广泛应用。

Thompson［2］通 过 现 场 测 试 发 现 ，钢 轨 的 一 阶Pinned⁃pinned（PP）共振是引起钢轨辐射噪声和钢轨波磨的主要原因，可采用钢轨阻尼器控制钢轨的一阶PP共振。Maes等［3］研究发现双调谐轨道阻尼器能够加强PP共振频率范围内的衰减率。通过研究总结钢轨振动特性，Croft等［4］研发出调频式钢轨阻尼器（Tuned Rail Damper，TRD）。此后，各种TRD被应用于轨道结构的减振降噪中。

文献［5］通过参数分析研究了TRD的质量、调谐频率、列车运行速度等参数对轨道结构振动的影响。文献［6］通过有限元计算和理论推导分析TRD对钢轨振动的影响，发现当TRD相对较长时，其一阶弯曲共振可能会影响轨道的振动特性。文献［7］发现TRD的刚体运动会导致轨道振动的能量耗散，因此弹簧质量模型能够满足分析要求。文献［8］基于傅里叶变换方法，研究了轨道结构动力学特性受钢轨阻尼器参数的影响。

文献［9］通过试验对约束型阻尼钢轨的振动进行分析，发现安装约束型阻尼器后钢轨高频范围内的振动衰减率明显大于未安装约束型阻尼器的振动衰减率。文献［10］利用室内消声测试方法对安装有迷宫式约束阻尼钢轨的振动和噪声特性进行了研究。文献［11］对安装TRD的钢轨振动衰减率进行了测试，认为TRD大大提高了钢轨特定频段内的振动衰减率。

既有TRD对振动衰减率影响的研究主要集中在TRD参数选取方面，而关于TRD安装位置对振动衰减率影响的研究较少。本文基于谱元法，建立计算模型，结合谱传递矩阵得出钢轨振动衰减率，研究调频式钢轨阻尼器安装位置对钢轨振动衰减率的影响。

1 计算方法

1.1 简化模型

钢轨用Timoshenko梁模拟，扣件视为弹簧-质量-弹簧系统［12］，TRD被简化为悬挂在钢轨单元节点处的质量-弹簧系统，计算模型见图1。其中：Ku，Kd分别为轨下垫板、减振器的刚度，kN/mm；Cu，Cd分别为轨下垫板、减振器的阻尼；ms为铁垫板质量，kg；K1，K2，K3为阻尼器刚度，kN/mm；m1，m2为阻尼器质量，kg。

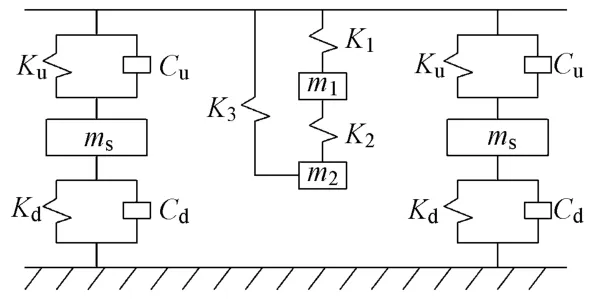
图1 计算模型

1.2 谱传递矩阵

材料均匀一致的等截面自由振动的Timoshenko梁运动方程为

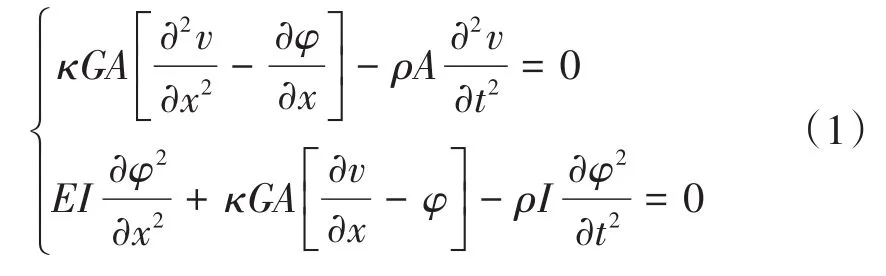
式中：v为梁横向位移，m；φ为梁截面转角，rad；E为杨氏弹性模量，GPa；I为截面惯性矩，m4；G为剪切模量，GPa；A为梁横截面面积，m2；ρ为梁密度，kg/m3；κ为剪切矫正因子，无量纲。

式（1）的解写成谱分量形式为

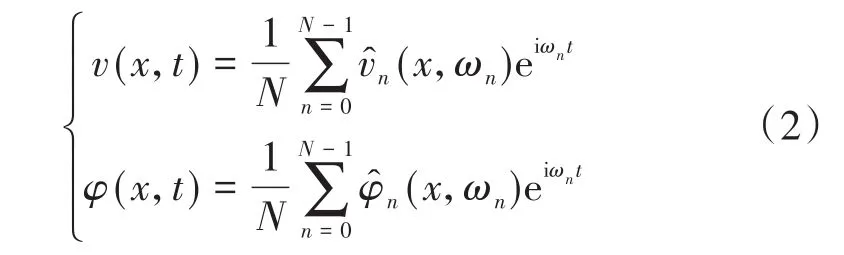
式中：N为时域采样点数；ωn为圆频率；t为时间。

将式（2）代入式（1），得

式（3）的一般解为

式中：v0，φ0为系数；k(ωn)为波数。

为方便表达，用k指代k(ωn)，用ω指代ωn。

将式（4）代入式（3），可得Timoshenko梁自由振动时的特征值问题，即

令式（5）中矩阵的行列式等于0，得频散关系

解式（6）可得波数k的4个解

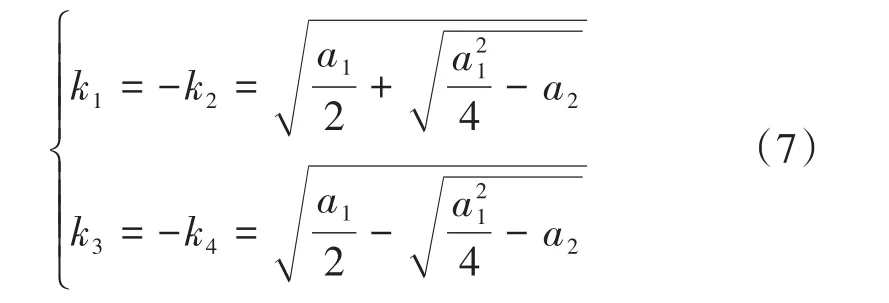
由式（5）可得v0和φ0幅值比

综上，式（3）的解为

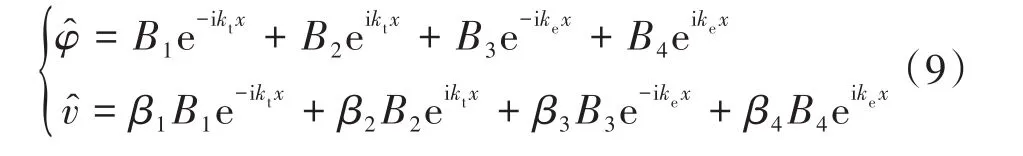
式中：B1，B2，B3，B4为待定系数项；kt=k1=-k2，含 kt的项表示往右传播的波；ke=k3=-k4，含ke的项表示往左传播的波。

根据谱元法，将相邻轨枕间的钢轨划分为1个Timoshenko梁单元，梁单元长为P，钢轨梁两端轨枕节点相当于梁单元的边界。谱节点位移向量和荷载向量分别为

对于自由振动的Timoshenko梁单元，梁内部横向剪切力V和弯矩M表达式分别为V= κGA(∂v/∂x- φ)，M=EI∂φ/∂x。

综上，谱元法钢轨单元的节点位移和结点力的关系为

式中：D（ω）为谱元法钢轨单元的谱刚度矩阵；d为谱单元节点的广义位移向量；f（ω）为广义力向量。

为方便推导，将梁单元的所有节点自由度分成3部分：左端（L）、内部（Z）和右端（R）。下文中下标中的L，R分别代表左端、右端。

谱刚度矩阵D（ω）可以表示为

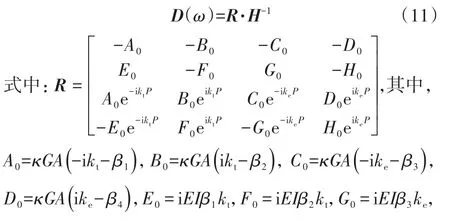
由于梁单元内部自由度不受外力，故f（Z）=0。

式中：Ti1为第i个元胞的谱传递矩阵；，分别为第i个元胞中钢轨左、右两边的状态向量。

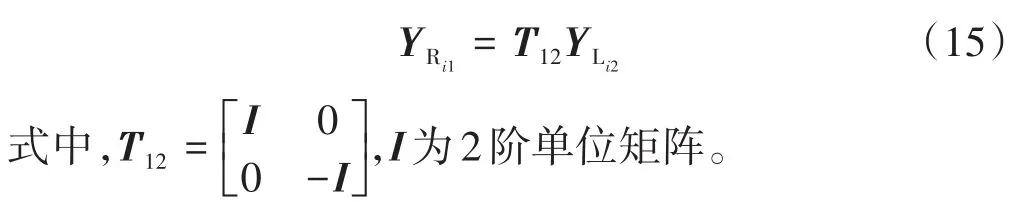
综上，可得钢轨单元的谱传递矩阵为

利用上述关系，可以得到钢轨元胞模型左右两端状态向量的传递矩阵为

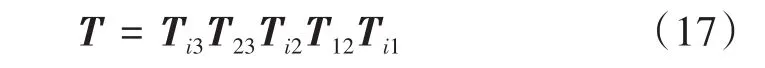
考虑到TRD的稳态动力学特性可用附加动刚度来描述，TRD单元对钢轨梁的附加动刚度Dr表达式为

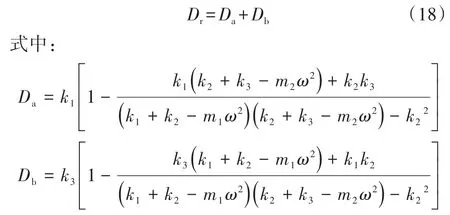
考虑附加质量-弹簧系统仅与钢轨单元的垂向位移自由度耦合，所以其谱单元刚度矩阵为

此时，钢轨单元的动态运动方程为

在谱元法中，轨下支承单元的谱传递矩阵的推导方法与钢轨单元谱传递矩阵的推导方法类似。

1.3 振动衰减率计算方法

作为钢轨的动态参数，振动衰减率指钢轨振动沿钢轨前进方向能量（振幅）传递的变化率，单位为dB/m。如果在某一频率范围轨道衰减率较小，表示此频率范围内轨道系统的动态阻尼较低，钢轨振动不能得到有效抑制。

由BLOCH定理，把式（16）转换成标准矩阵特征值问题，即

式中：I为2阶单位矩阵；kx为一维BLOCH波矢。

对于图1所示的悬挂有TRD系统的轨道结构，T的表达式为

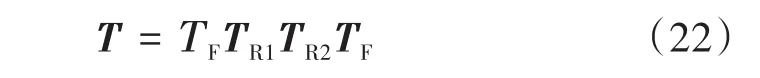
式中：TF为轨下支承的谱传递矩阵；TR1，TR2分别为TRD安装在右、左节点的钢轨单元谱传递矩阵。

对复波数k=kr+iki（ki为负数）的一个单波，每传播1 m，振幅减少exp（ki），衰减率可表示为Δ=-20lg[exp(ki)]=-8.686ki，即衰减率为波矢虚部的-8.686倍。因此求得波矢kx与频率ω的关系后，可通过Δ=-8.686Im(kx)求得钢轨振动衰减率。

本模型中，BLOCH波矢的解总以±kx的形式成对出现，分别反映同一种波沿相反方向的传播特性。

2 TRD对振动衰减率的影响

计算模型中各部件振动衰减率参数见表1。

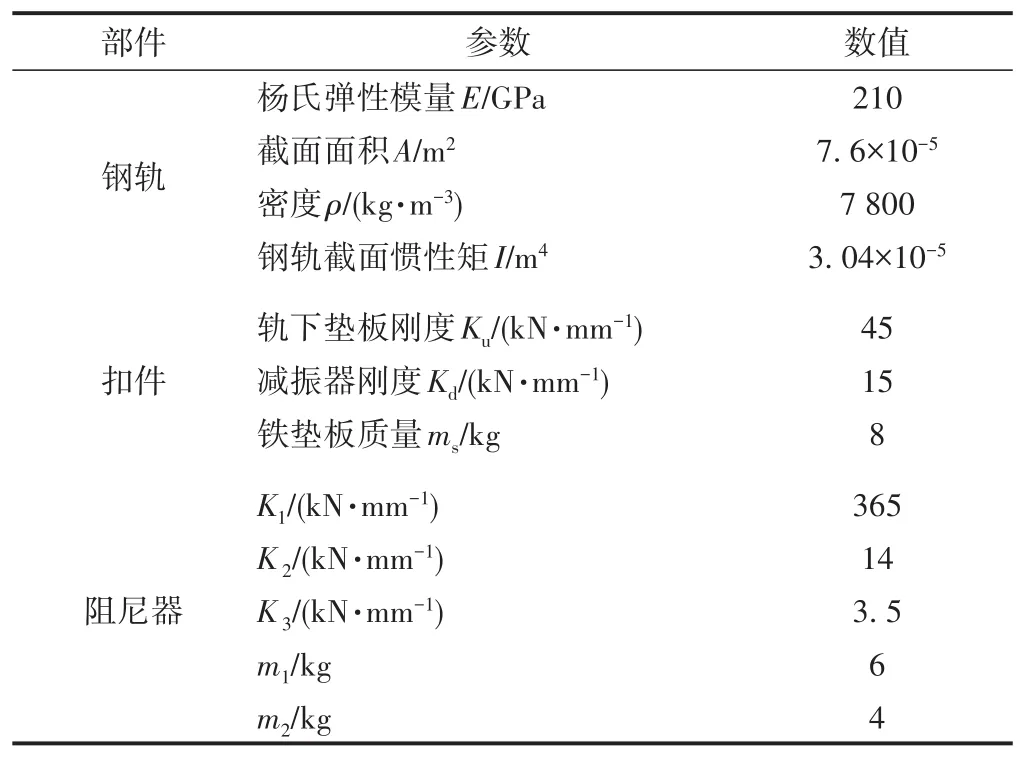
表1 振动衰减率参数

计算未安装TRD时振动衰减率，结果见图2。可知，轨道结构纵向存在2种形式的波。一种波在全频段都有较高的衰减率，只有在83，450 Hz附近小范围内衰减率低于10 dB/m，说明这种波很难沿着轨道结构纵向传递，称之为衰减波；相反，另一种波只在某些频段维持较高的衰减率，其余频段轨道衰减率接近0，称之为传播波。钢轨振动特性主要由传播波决定。在研究钢轨振动特性时，只需要考虑传播波的衰减率。

图2 未安装TRD时的振动衰减率

分别计算安装TRD前后钢轨的振动衰减率，其对比结果见图3。

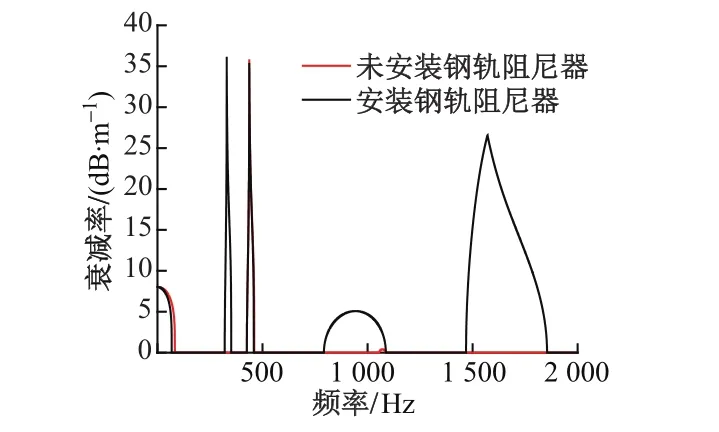
图3 安装TRD前后钢轨振动衰减率对比

从图3可知，TRD对振动衰减率影响很大。未安装TRD时，只有0～83 Hz及450 Hz附近衰减率较高。在1 000 Hz（钢轨的一阶PP共振频率）附近衰减率虽然也出现峰值，但相对较小，对钢轨振动的抑制效果不大。弹性波在沿钢轨纵向传播的过程中会在特定频段出现振动衰减率突然增大现象，表示此频率范围内轨道系统的动态阻尼较高，钢轨的振动得到有效抑制，这些特定的频率范围称为带隙。

安装TRD后，轨道结构在保持原有带隙基本不变的同时，在300，1 700 Hz附近均出现新的带隙。在钢轨一阶PP共振频率附近的带隙被大大拓宽，相应的衰减率峰值也得到提高，说明TRD能够在自身工作频率范围内有效抑制钢轨振动。

3 TRD安装位置偏差对振动衰减率的影响

工程中要求TRD对称安装于钢轨轨腰两侧。事实上TRD的安装位置会有一定偏差。为了研究TRD安装偏差对振动衰减率的影响，分别计算不同l取值下轨道的振动衰减率，见图4，其中l为从钢轨阻尼器中心到钢轨跨中距离的2倍。无偏差时l=0。

图4 不同l取值下轨道的振动衰减率

从图4（a）可以看出，l=0.001 mm时，曲线与l=0几乎重合，说明当l取值特别小时l的取值不会对振动衰减率产生影响。增大l的取值，当l=0.01 mm时，振动衰减率在1 400 Hz附近出现新的带隙，说明此时TRD的安装位置开始对振动衰减率产生影响。

继续增大l的取值，从图4（b）可以看出，随着l从0.1 mm增大到0.3 mm，新出现的带隙被不断拓宽，同时衰减率峰值也有一定程度增加，但两侧带隙变窄。l=0.3 mm时，新出现的带隙达到最宽，而相应的两侧带隙几乎消失。

从图4（c）可以看出，增大l至0.4 mm时，轨道衰减率出现了与之前相反的变化趋势，新出现的带隙开始变窄，相应的两侧带隙变宽。l增大至0.4，0.5 mm，新出现的带隙宽度持续减小。

从图4还可以看出，TRD安装位置发生变动时，振动衰减率仅在500 Hz以上有较大变动。

综上，可以认为TRD的安装位置偏差会对振动衰减率产生影响，且只体现在500 Hz以上高频部分，对于500 Hz以内的振动衰减率几乎不会产生影响。

4 结论

本文基于谱元法，建立了钢轨、扣件、调频式钢轨阻尼器（TRD）计算模型，结合谱传递矩阵，得出钢轨振动衰减率，并对TRD安装位置对钢轨振动衰减率的影响进行了分析，结论如下：

1）TRD能大幅度提高在自身工作频率附近的振动衰减率，合理选择TRD的参数能有效控制轨道结构的振动。

2）TRD的安装偏差会对振动衰减率产生影响，且主要体现在500 Hz以上的高频部分，对500 Hz以内的振动衰减率几乎不会产生影响。