缓和曲线过渡段长度对地铁车辆动力性能的影响

胡齐斌 罗世辉 马卫华

（西南交通大学牵引动力国家重点实验室，成都 610031）

线路的线型对铁道车辆动力学性能有较大影响，故在铁道线路的直线段和圆曲线段之间通常会设置缓和曲线，使得轨道的曲率及超高能够平稳过渡。在缓和曲线范围内，线路曲率由无限大逐渐过渡到与圆曲线相等，以利于行车平稳；外轨超高由0逐渐增加到圆曲线的超高值，从而使车辆向心力的增加和离心力的增加相匹配，以减小车辆通过突变点时轮轨冲击，增加车辆运行的安全性和乘坐舒适性［1-2］。对此，国内外学者分析了不同类型的新型及改善型缓和曲线［3-6］。

城市轨道交通线路多曲线且多为小半径曲线。在线路缓和曲线及其过渡段设计方面，Ansari等［7］对德黑兰的一条地铁线路进行了实地测量，确定了不同曲线上车轮磨损率；许国平等［8］对比研究了高速铁路不同缓和曲线线型始终点动力学参数的突变值。对于缓和曲线段与直线段及圆曲线段间连接处的研究，杨达鹏［9］提出了在超高顺坡始终点处设置竖曲线来改善行车的平稳性；俞友强［10］阐述了通过消顶补坑法来使缓和曲线线型更加平顺、合理；杨久川等［11］研究发现缓和曲线越短，竖曲线半径越小，关键点处的轮轨冲击振动越剧烈。

目前有少数地铁车辆在部分线路上运行时会出现高度阀偏离安装位置，甚至出现安装座断裂的情况。根据该情况，本文对地铁车辆在曲线段尤其是缓和曲线段与直线段和圆曲线段之间的过渡段进行动力学仿真分析。

1 影响车辆曲线通过性能的因素

根据外轨超高的顺坡形式，将缓和曲线线型划分为直线型和曲线型。

直线型超高顺坡缓和曲线在直缓和缓圆接点处存在折角，超高在缓和曲线始终点突变，从而使得车辆通过该处时骤然产生附加作用力和冲击。

直线型超高顺坡缓和曲线在垂直面内的变化如图1所示。其中：ZH代表直缓段；HY代表缓圆段；u（s）为轨道超高变化量；L为轨道长度变化量；h为直缓及缓圆连接点所在处的过渡段长度；l0为缓和曲线的长度；u0为轨道圆曲线处的超高值。

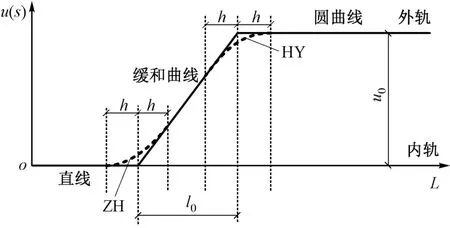
图1 直线型超高顺坡缓和曲线在垂直面内的变化

本文中缓和曲线段与直线段和圆曲线段之间的接点即直缓点、缓直点、缓圆点、圆缓点所在的区间，即为缓和曲线过渡段。

由于各过渡段连接点处存在超高角或折角，使得外轨为折角顺坡，折角越小，车辆通过时发生的冲击越大，所受的突变轮轨力越大。折角问题可通过将折角顺坡改为竖曲线顺坡或通过改变缓和曲线始终点的平滑程度来解决，即让过渡段更加平缓，使缓和曲线两端能较好地平滑过渡。

地铁线路空间较小，小半径曲线较多，故大多选用直线型超高顺坡缓和曲线或改善型缓和曲线。我国地铁车辆的行车速度一般在50～80 km/h，其轨道缓和曲线线型通常采用直线型超高顺坡三次抛物线［12］。本文针对这一缓和曲线线型进行研究。

2 动力学仿真分析

2.1 动力学模型

以SIMPACK软件为基础，采用时速100 km地铁A型车的结构及主要参数，借用同类地铁所用的无摇枕型动车转向架的结构参数，建立考虑了高度阀的动力学整车及轨道模型，见图2（a）。每个转向架设2个高度阀，1节车共4个，高度阀局部放大见图2（b），其中短臂与车体铰接，长臂与转向架铰接，短臂与长臂铰接，并对短臂和长臂的运动进行了约束，使得短臂只能绕x轴转动，长臂可绕x和y轴转动。

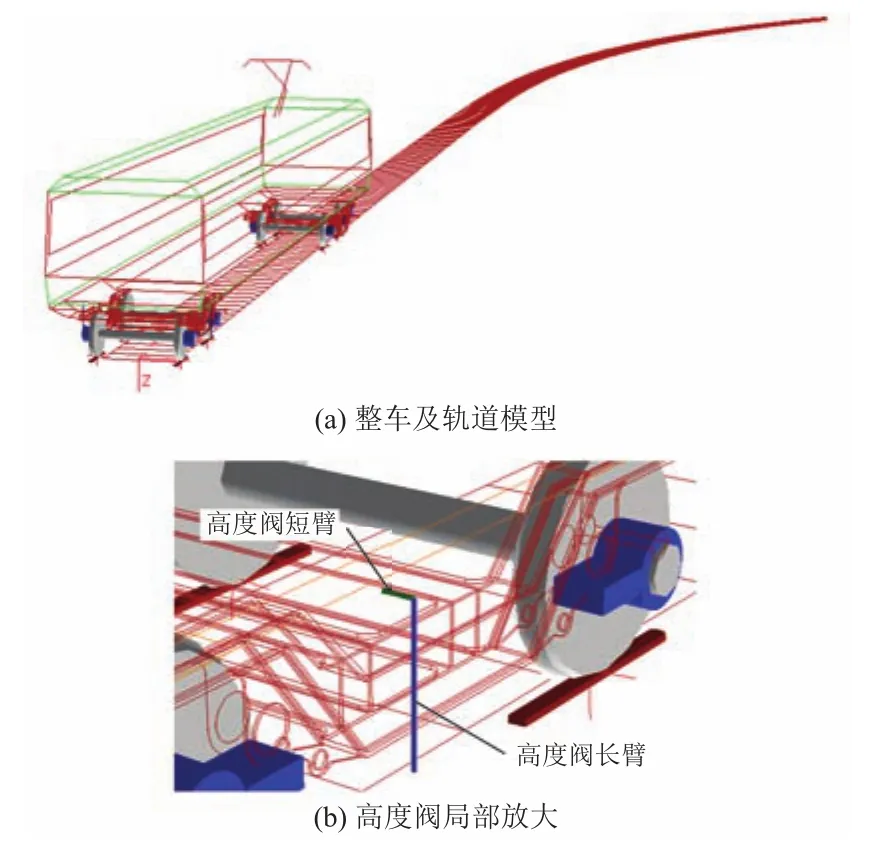
图2 SIMPACK动力学仿真模型

线路线型设置为直线-缓和曲线-圆曲线-缓和曲线-直线。第1段直线、缓和曲线和圆曲线长度分别为50，40和300 m，线路总长2 361m。由于空间用地等原因，为使结果更具代表性，将曲线段半径设置为400 m，并将曲线顺坡按较恶劣情况考虑，顺坡坡度取0.3%，超高取120 mm，轨底坡取1︰40，仿真计算时取1个完整的进出曲线过程。

整车模型部分参数见表1，高度阀刚体参数见表2。

表1 整车模型部分参数

表2 高度阀刚体参数 mm

2.2 分析方法

通过仿真高度阀偏离安装位置，观测其短臂和长臂的转动角度，并分析高度阀发生异常现象时其短臂与车体铰接处及长臂与转向架铰接处所受的横向力和垂向力，以及同一里程处的车辆轮轨力。

在SIMPACK软件中设置缓和曲线超高顺坡类型为直线型，通过考虑不同缓和曲线过渡段长度和不同车辆运行速度来进行动力学仿真分析。通过对比分析同一里程处不同参数条件下各项动力学性能参数的变化规律，得出问题的原因及解决问题的方法。

2.3 分析结果

2.3.1 过渡段长1 m时车辆的动力学性能参数

1）高度阀长短臂转动角度

车辆以20，40，60，80，100 km/h的速度通过过渡段长1 m的缓和曲线段时，分别对高度阀的短臂和长臂的转动情况进行观测。在速度60 km/h之后高度阀严重偏离安装位置，高度阀长臂最大转动角度均出现在绕x轴转动时，见表3。选取接近国内地铁车辆常用最高时速80 km/h时的情况进行详细分析。

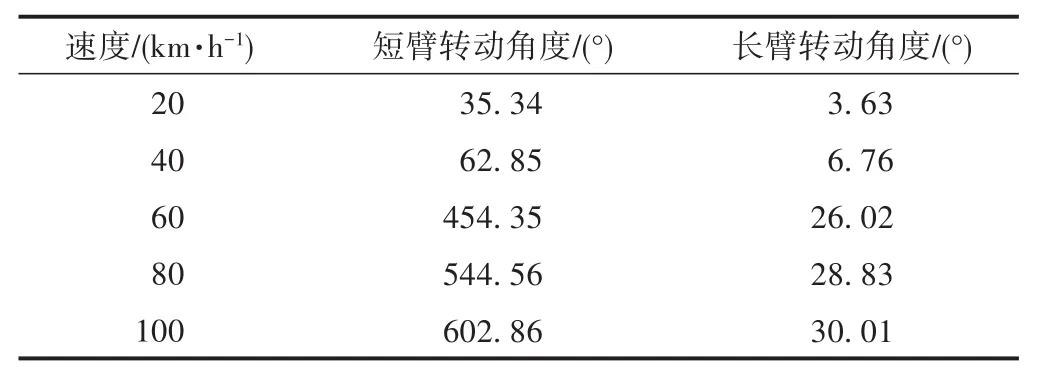
表3 不同车速下高度阀绕x轴的最大转动角度

在车速80 km/h、过渡段长1 m时前后转向架的左右侧高度阀转动角度变化曲线见图3。可以看出：①当车速80 km/h、过渡段长1 m，车辆进出缓和曲线时，前后转向架左右高度阀均发生了偏转；②高度阀短臂转动角度有超过360°的情况，即发生了翻转；③前转向架右侧位于低轨侧，车辆进出曲线时右侧短臂均发生了翻转，故其又回到了初始位置；④后转向架左侧位于高轨侧，左侧短臂只发生了1次翻转，而后继续同向转动，出曲线时保持偏转状态并未回到初始位置；⑤剩余的2处短臂只发生了偏转，并未翻转，出曲线后均未回到初始位置；⑥对于前后转向架高度阀的长臂，在车辆进出曲线发生了偏转之后，只有前转向架右侧的长臂重新回到了初始位置，剩余的3处长臂均保持偏转后的状态。以上状态与实际运行中出现的问题相符。

从图3还可以看出，在车辆通过直缓点、缓圆点、圆缓点和缓直点4处时，高度阀的短臂和长臂的转动角度均有较大波动且有突变的情况发生，这说明缓和曲线过渡段对车辆曲线通过性能有明显影响。

2）高度阀长短臂安装座受力

对车速80 km/h、过渡段长1 m时高度阀严重偏离安装位置作进一步分析。高度阀长短臂安装座受力见图4和图5。

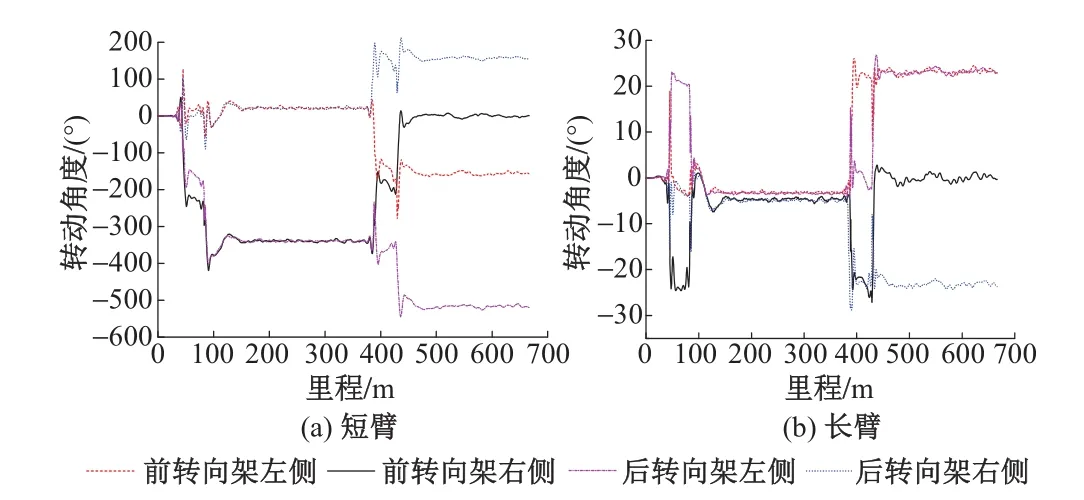
图3 车速80 km/h、过渡段长1 m时高度阀转动角度变化曲线

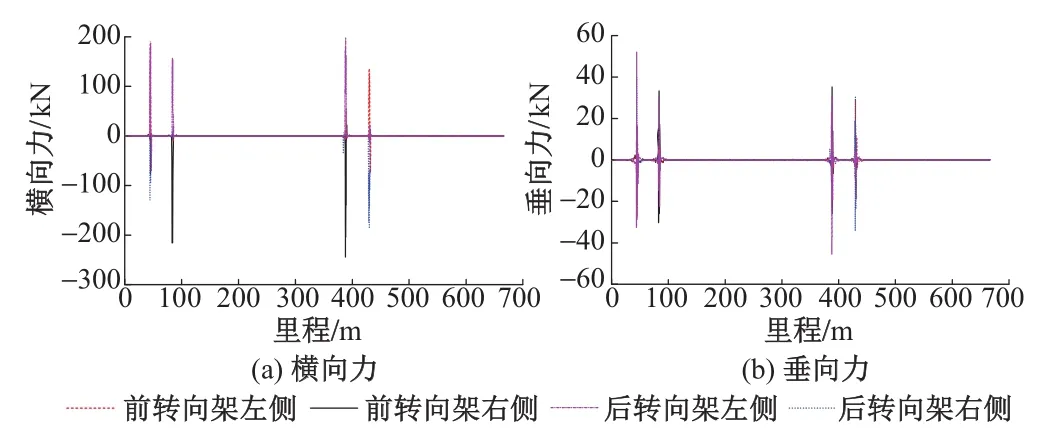
图4 高度阀短臂安装座受力曲线

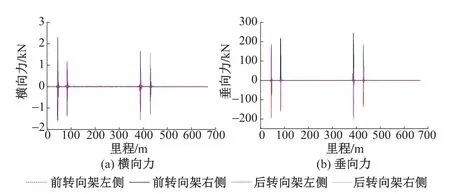
图5 高度阀长臂安装座受力曲线

由图4和图5可以看出：①在车辆通过缓和曲线过渡段时高度阀短臂和长臂的安装座受力均发生了突变。其中短臂安装座所受横向力突变值过大，且大于其垂向力突变值；长臂安装座所受垂向力突变值过大，且大于其横向力突变值。②短臂安装座固结于车体，而长臂安装座固结于转向架，说明车辆在通过缓和曲线过渡段时，车体与转向架之间突然产生的横向相对位移较大，致使转向架传递给高度阀的横向突变力较大。③由长臂安装座受力可知转向架传递给高度阀的垂向突变力也较大，这说明车辆通过缓和曲线过渡段时转向架明显受到冲击。由于转向架所受的力是由轮轨力传递来的，可知轮轨力在同一里程处发生了突变，并将突变力传递至转向架上。④高度阀长短臂安装座受力发生突变时的里程与高度阀长短臂转动角度突变时的里程一致，均发生在缓和曲线过渡段上，并由力的传递说明轮轨力也在同一里程处受到了缓和曲线过渡段的影响。

3）轮轨力

由上文分析可知，在车辆通过缓和曲线过渡段时，各转向架受力均发生了突变。选取前转向架的各车轮轮轨力进行分析。车速80 km/h、过渡段长1 m时前转向架轮轨力曲线见图6。其中：1L，1R为前轮对的左右车轮；2L，2R为后轮对的左右车轮。

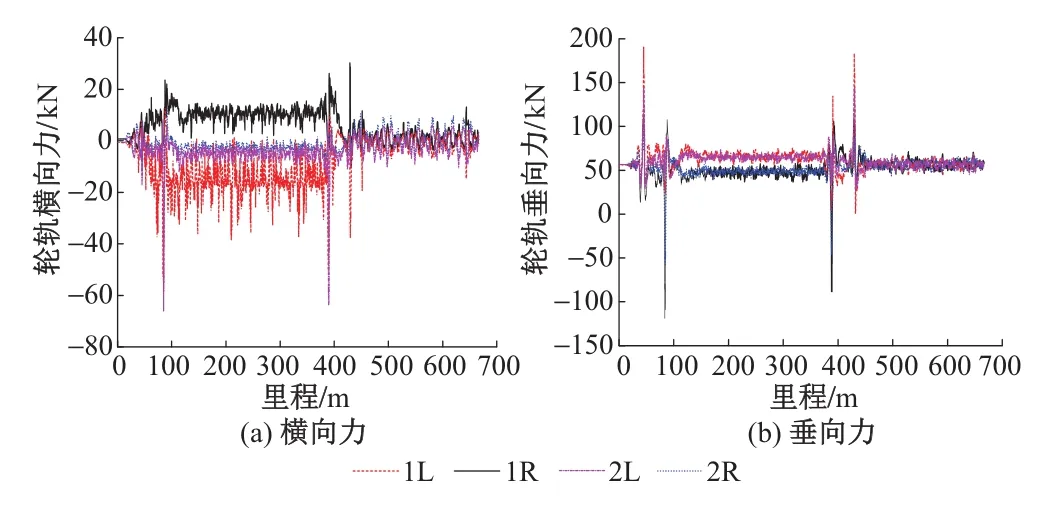
图6 车速80 km/h、过渡段长1 m时前转向架轮轨力曲线

从图6可以看出：在车辆通过缓和曲线过渡段时，在高度阀长短臂安装座受力发生突变的同一里程，轮轨横向力和垂向力均发生了突变，说明高度阀偏离安装位置是由于轮轨力突变，通过转向架将突变力传递至高度阀所致。因轮轨横向力和垂向力的突变值过大，由于力的传递转向架上如高度阀一类的零部件会受到过大冲击，且随着冲击次数的增多这些零部件会发生损坏。

从图6（b）还可以看出，曲线低轨侧（即转向架右侧）的轮轨垂向力突变时其为极大负值，说明此时车辆通过时车轮发生严重的瞬间抬起现象，已出现运行安全问题。

2.3.2 过渡段长2 m时车辆的动力学性能参数

车速不变，将缓和曲线过渡段长度加长至2 m，再次进行仿真，对比同一里程处、同一高度阀短臂的转动角度以及同一转向架各车轮的轮轨力。

车速80 km/h、车辆通过长2 m的缓和曲线过渡段时高度阀短臂转动角度变化曲线见图7，前转向架轮轨力变化曲线见图8。

图7 车速80 km/h、过渡段长2 m时高度阀短臂转动角度变化曲线

图8 车速80 km/h、过渡段长2 m时前转向架轮轨力变化曲线

从图7可以看出：在增加缓和曲线过渡段长度之后，高度阀偏转的问题得到很大改善，虽然在缓和曲线过渡段处仍有突变现象，但实际转动角度明显减小，其中短臂转动角度的最大值未超过45°，在高度阀正常工作范围内。

对比图6和图8可以看出：轮轨垂向力大大减小，最大值约为过渡段长1 m时最大值的1/2，轮轨横向力也有一定的减小，且突变现象也得到一定改善。

通过以上分析说明，缓和曲线过渡段长度对车辆轮轨力尤其是轮轨垂向力有较大影响，且对车辆通过缓和曲线过渡段时所受冲击力大小也有较大影响。缓和曲线过渡段长度越大，轮轨力减小的程度越大。因此，高度阀偏离安装位置或其安装座损坏主要是由于车辆通过缓和曲线过渡段时产生异常轮轨力及异常冲击所致，而究其根本原因是由于缓和曲线过渡段长度设置不合理，缓和曲线两端没有较好地平滑过渡。

2.3.3 缓和曲线过渡段合理长度的确定

前转向架上最大轮轨力随缓和曲线过渡段长度的变化曲线见图9。

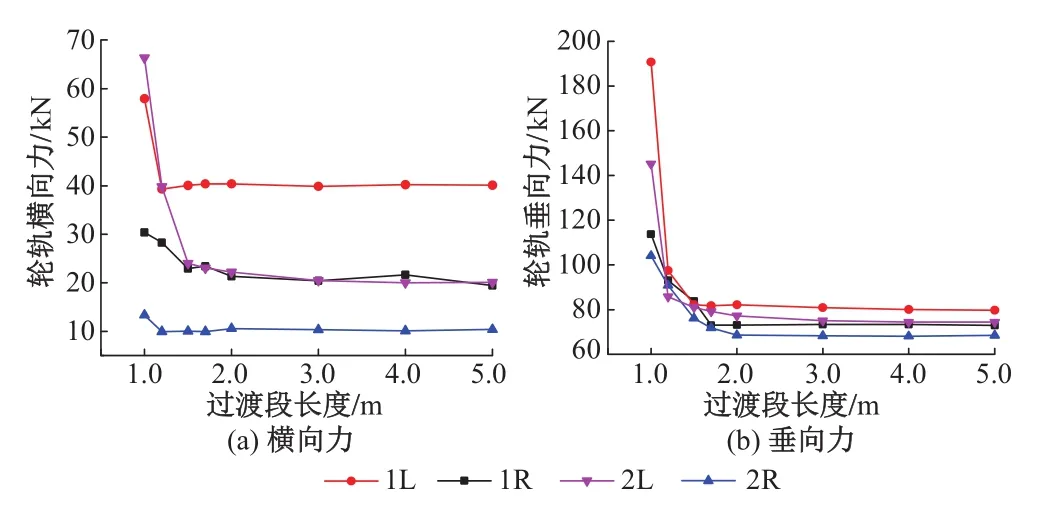
图9 前转向架最大轮轨力随缓和曲线过渡段长度变化曲线

从图9可以看出，轮轨力随着缓和曲线过渡段长度的增加而减小。缓和曲线过渡段长3 m时轮轨力基本不再变化，说明缓和曲线过渡段长度并不是越长越好，同一车速下其改善效果具有极值。

车速80 km/h时前转向架各车轮脱轨系数和轮对轮重减载率随缓和曲线过渡段长度变化曲线见图10。

图10 车速80 km/h时前转向架各车轮脱轨系数和轮对轮重减载率随缓和曲线过渡段长度变化曲线

从图10可以看出：在线路其他条件不变的情况下，随着缓和曲线过渡段长度的增加，脱轨系数和轮重减载率均明显减小，过渡段长2 m时两者均趋于稳定。这也说明在同一车速下，通过增加过渡段长度来改善车辆动力学性能具有极限。

车速80 km/h时，缓和曲线过渡段长度h≥1.5 m的区间脱轨系数均小于1，轮重减载率均小于0.6，两者均满足规范［13］要求。结合图9可以得出，在脱轨系数和轮轨减载率满足规范要求的前提下，既要使轮轨间的受力得到最大改善又要平衡工程量和经济性，缓和曲线过渡段长度至少达到3 m。

3 结论

1）当地铁车辆通过直线型超高顺坡缓和曲线段时，各车轮所受轮轨力最大值出现在缓和曲线过渡段，即直缓段、缓圆段、圆缓段和缓直段的连接点处。

2）车辆通过缓和曲线过渡段时，各车轮因受冲击产生的轮轨力突变值会受到过渡段长度的影响，且缓和曲线过渡段处外轨对车轮的影响更大。随着缓和曲线过渡段长度的增大，轮轨力突变值会逐渐减小。同一车速下过渡段长度达到一定值后轮轨力基本不再变化，即对轮轨力突变的改善效果具有极值。在实际工程中应结合实际车速适当设置过渡段长度。

3）对于地铁车辆，受运行条件限制，可通过优化线路设计来改善车辆的曲线通过性能。