基于量子力学的单分子弹性理论模型研究

2020-04-02解枭雄王俊元

机械设计与制造工程 2020年2期

解枭雄，成博，刘峰，王俊元

(中北大学机械工程学院，山西太原 030051)

近年来，随着纳米技术的发展，基于原子力显微镜的单分子力谱由于其高灵敏度和可操作性，已经成为纳米尺度上测量各种分子内、分子间以及界面间相互作用力的有效工具[1-3]。经过近20年的发展，基于单分子力谱的实验研究方法已经广泛应用在各个方面，包括高分子链的本征弹性、超分子结构的相互作用力、固-液界面间的解吸附力以及分子马达的组装力等[4-8]。尤其在单分子纳米力学研究中，测定单个聚合物链的纯弹性力学性能可以被用来揭示其分子的构象转变、链结构形态以及聚集态形态等诸多行为的内在机理[9-12]。与逐渐成熟的单分子实验研究相比，相应的弹性理论模型研究却进展缓慢，而这对于人们更进一步地理解单分子链弹性行为非常重要。到目前为止并没有一种准确的数学模型被用来描述单个聚合物分子链的理论弹性行为。

之前，基于Flory等[13]的工作，自由结合链(freely jointed chain，FJC)模型、自由旋转链(freely rotating chain，FRC)模型和蠕虫状链(worm-like chain，WLC)模型作为3个基本的弹性理论模型被用来描述高分子的单链弹性行为。然而，随着单分子实验技术的发展，发现这3种理论模型并不能很好地描述高分子链的弹性行为，这是因为该理论模型仅考虑熵弹性对分子链弹性的影响，并没有考虑焓弹性(键长和键角的改变)对其的影响[14-17]。2005年，Hugel等[16]通过采用基于量子力学(quantum mechanics)的从头计算法(ab-initio calculations)对几种典型高分子的重复单元进行了理论弹性计算，通过对STO-6G、TZV和MP2/TZV等3种基组算法进行比较，发现MP2/TZV理论能够更准确地描述高分子的焓弹性。结合MP2/TZV理论的量子力学计算结果，Cui等[17]在此基础上，将焓弹性引入到3种基础模型中，进而发展了3种新的模型，即基于量子力学计算的QM-FJC模型、QM-FRC模型和QM-WLC模型。近年来他们进行了一系列高分子的单分子力谱实验，结果已经证明这些模型可以很好地描述一些聚合物单个分子链的本征弹性，比如含C-C骨架的聚合物、天然纤维素、DNA、蛋白质等高分子[8,18-19]。但是，这3种模型对于各类高分子的适用性却鲜有报道。

1 单分子力谱实验

材料和样品准备：左旋聚乳酸与实验中所用试剂(分析纯)，均购自西格玛奥德里奇中国公司；蛋白质I278是由8个I27(肌联蛋白的第27个结构域)聚合而成，购自美国雅典娜环境科学公司。在进行单分子力谱实验之前，首先将样品(PLLA和I278)溶解于相应的溶剂(二氯甲烷和水)中并稀释，最终配置成浓度为1 μg/ml的稀溶液，然后取少量样品溶液置于新鲜基底(石英片或金片)上物理吸附0.5 h，最后使用去离子水对其进行冲洗，去掉吸附不牢固的分子，完成制片。

所有的单分子力谱实验均在原子力显微镜(MPF-3D,Asylun Research, CA)上完成。实验前在原子力显微镜针尖与样品之间加入少许壬烷，以保证针尖处于液相环境中，当针尖压向基底表面捕捉到样品分子时，针尖与基底会形成分子桥，接着随着针尖从基底上远离，分子链被拉伸直至断裂。在针尖的整个运动过程中，固定针尖的微悬臂与针尖的运动位移被记录下来并且最终转化为拉伸力与拉伸长度相关的曲线图。实验所使用的针尖为氮化硅针尖，拉伸速率为2 μm/s。

2 结果与讨论

本文选取两种典型高分子左旋聚乳酸(PLLA)和聚蛋白质(I278)作为研究对象，测得其在非极性有机溶剂壬烷中的单分子弹性曲线，再分别利用QM-FRC、QM-FJC以及QM-WLC 3种模型来拟合所得实验曲线，并且通过计算拟合曲线和实验曲线之间的平均力值偏差来比较和分析3种模型对于高分子的适用性。

众所周知，当一个高分子链处于非极性有机溶剂中时，由于分子链与溶剂分子之间除了存在范德华相互作用并无其他特殊的相互作用，这可以用来近似模拟理论计算中的真空环境，因此高分子链在非极性有机溶剂中的单分子力谱通常可以表征其本征弹性[7,14]。

首先笔者利用原子力显微镜测得左旋聚乳酸(PLLA)在非极性有机溶剂——壬烷中的单分子力谱。从图1中可以看到这是一个典型的力-距离拉伸曲线(简称力曲线)，当分子链拉伸超过其轮廓长度之后，开始表现出它的弹性，随着分子链长度的不断伸长，力随着拉伸长度也在增加，直到分子链与基底或者针尖之间的分子桥断裂，拉伸力骤减为0。由于每次拉伸实验过程中不同分子链的拉伸距离不同，因此无法进行统一的比较和分析，需要将曲线进行归一化处理[14]。如图2所示，经过对实验曲线进行归一化后，发现这些曲线都可以很好地重合在一起，表明所得到的力曲线是PLLA在非极性有机溶剂中的单链拉伸行为，也就是单个PLLA链的本征弹性。

图1 多个PLLA单分子链(不同长度)在非极性有机溶剂(壬烷)中被拉伸所获得的力曲线(不同的轮廓长度)

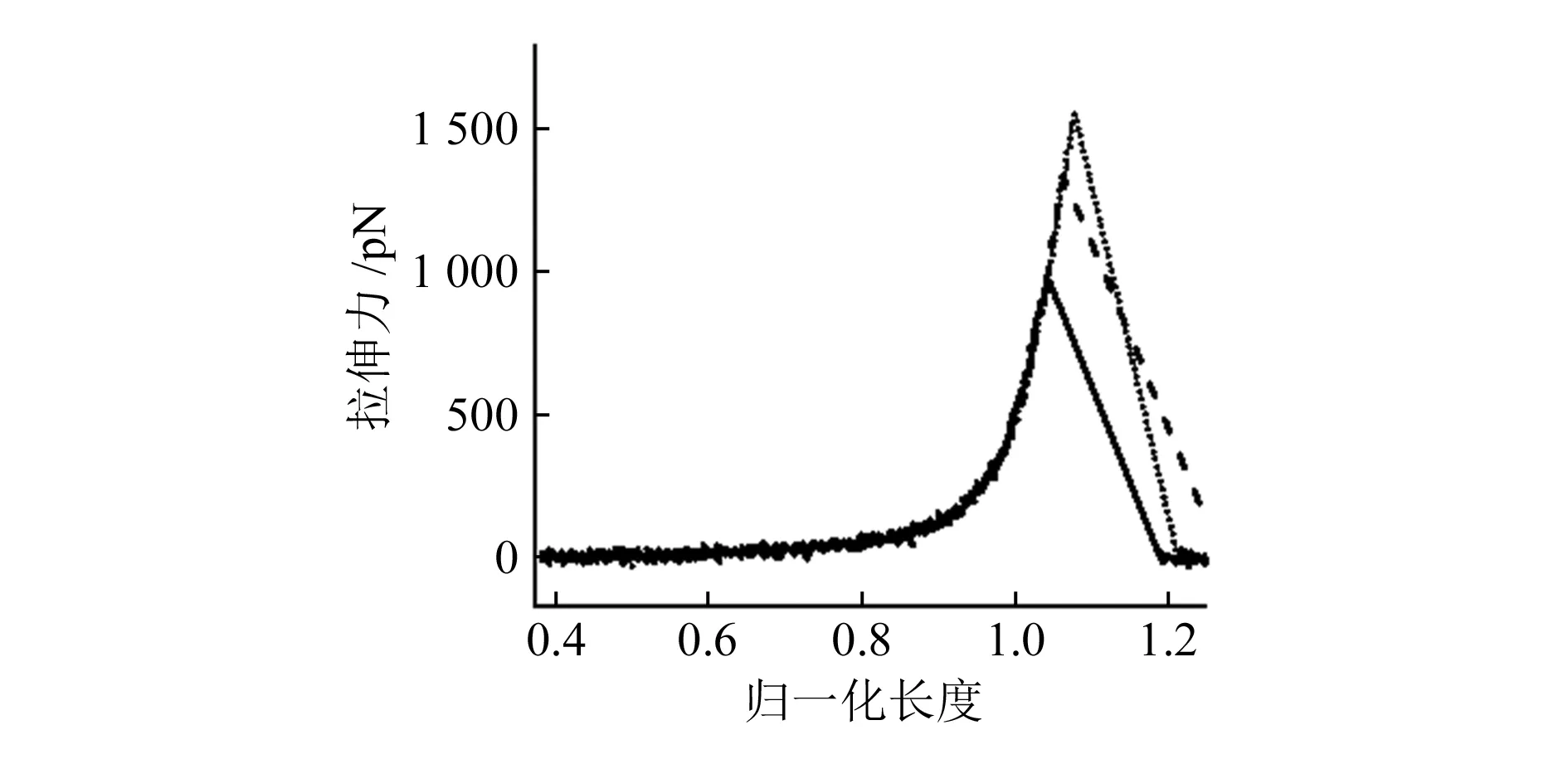
图2 归一化后的不同轮廓长度力曲线

接着笔者以FJC、FRC以及WLC模型作为基础，利用量子力学的从头计算法，基于MP2/TZV理论，分别计算出这两种高分子单个重复单元的理论焓弹性，进而将两者结合发展成为新的基于量子力学计算的QM-FJC、QM-FRC以及QM-WLC模型。

FJC模型的数学表达式：

(1)

FRC模型的数学表达式：

(2)

WLC模型的数学表达式：

(3)

式中：R为在力F作用下高分子链末端距；F为高分子链端所受到的拉伸力；L0为分子链在自由状态下(即F=0)的轮廓长度；LF为分子链在力F作用下的轮廓长度；kB为波尔茨曼常数；T为绝对温度；lk为库恩长度；lb为旋转单元长度；lp为持续长度。

基于MP2/TZV理论的量子力学计算结果为：

(4)

式中：γn为多项式系数，其中γ1为线性弹性模量，其余的为非线性修正系数，n为多项式阶数，用来修正非线性弹性模量的重要物理量，与量子力学计算结果有关。PLLA与聚蛋白的量子力学计算结果见表1。

表1 PLLA与聚蛋白的量子力学计算结果 nN

通过将3种基本模型与量子力学计算结果相结合，从而得到3个新模型，即QM-FJC、QM-FRC以及QM-WLC模型。在这3个新模型中，每个模型仅有一个变量(lk,lb,lp)，当给定一个确定值时，就可以产生一条相应的理论拟合曲线。

使用这3种新模型分别去拟合所得到的实验曲线[8,14]。为了找到最佳的拟合参数值，计算实验曲线与理论模型拟合曲线的力值平均偏差ΔF:

(5)

式中：Fexp为实验曲线上某数据点处的拉伸力；Ffit为模型拟合曲线上该数据点处的拉伸力值；n1为曲线上数据点的数量。

经过拟合后，从图3可以发现，当lb=0.36 nm时，QM-FRC模型拟合曲线与实验曲线的力值平均偏差最小(ΔF1=11.957 22 pN)，因此lb=0.36 nm是QM-FRC模型拟合PLLA分子链本征弹性曲线的最佳值。经过与实验曲线对比(如图4所示)，发现两者可以在整个力值区间内很好地重合，而且0.36 nm正好是PLLA单个结构单元的长度[20]，说明该参数与结构相关。当lk=0.72 nm时，QM-FJC模型拟合曲线与实验曲线的力值平均偏差最小(ΔF2=11.934 16 pN，如图5所示)，因此lk=0.72 nm是QM-FJC模型拟合PLLA分子链本征弹性曲线的最佳值。通过将此值所对应的QM-FJC模型拟合曲线与实验曲线对比(如图6所示)，可以看出两者可以很好地重合，而且lk=0.72 nm正好是lb=0.36 nm的2倍，这也表明该模型是个与结构参数相关的模型。

图3 不同lb值下的QM-FRC模型拟合曲线与实验曲线之间的力值平均偏差示意图

图4 PLLA在壬烷中获得的力曲线(实线)与QM-FRC模型最佳拟合曲线(虚线)对比图

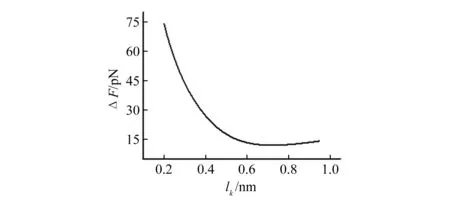
图5 不同lk值下的QM-FJC模型拟合曲线与实验曲线之间的力值平均偏差示意图

图6 实验曲线(实线)与QM-FJC模型拟合曲线(虚线)对比图

将QM-FJC和QM-FRC模型拟合曲线与实验曲线的力值平均偏差进行比较，发现其差距仅有0.015 6 pN。为了进一步理解该现象，笔者将QM-FJC与QM-FRC拟合曲线进行比较，如图7(a)所示，可以发现这两条曲线并无较明显差别，基本可以很好地重合，仅在15 pN以下有些不同(如图7(b)所示)。然而由于单分子力谱实验曲线在15 pN以下的范围内分辨率并不高，因此QM-FJC与QM-FRC模型拟合曲线的差距可以忽略，说明这两种模型都可以描述单个PLLA链的本征弹性行为。而对于QM-WLC模型，当lp=1.37 nm时，拟合曲线与实验曲线的力值平均偏差最小(ΔF3=24.131 9 pN，如图8(a)所示)。对拟合曲线和实验曲线进行比较，如图8(b)所示，发现在大多数力值区域内两者可以很好重合，但是在中低力区却不能很好重合。这说明虽然此模型也可以用来描述其单个PLLA链的弹性行为，但是相比于QM-FRC和QM-FJC模型在中低力区还是有明显的差距，也就是说，QM-WLC模型并不能够准确描述PLLA单分子链的自身弹性行为。

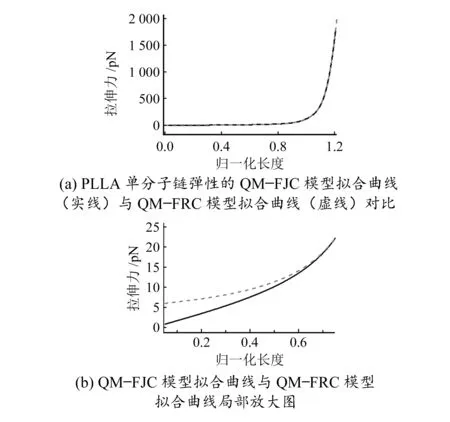
图7 QM-FJC与QM-FRC模型拟合曲线对比

图8 PLLA实验曲线与QM-WLC模型拟合曲线对比

随后，笔者又测得了另一种高分子——聚蛋白质在壬烷中的单分子力谱(如图9所示)，并利用这3种模型拟合了单个解折叠的蛋白质链的单分子本征弹性行为，发现当lp=0.38 nm时，QM-WLC模型拟合曲线与实验曲线的力值平均偏差最小(ΔF4=27.611 6 pN，如图10(a)所示)，即此值为最佳拟合值。通过与实验曲线对比，如图10(b)所示，发现当lp=0.38 nm时，QM-WLC模型拟合曲线与实验曲线可以在整个力区内很好地重合，说明该模型可以用来描述单个解折叠蛋白质链的本征弹性行为。另外，0.38 nm正好是解折叠蛋白质链的一个结构单元长度[21]，说明该参数与结构相关。当lb=0.11 nm时，QM-FRC模型拟合曲线与实验曲线的力值平均偏差最小(ΔF5=42.227 01 pN，如图11(a)所示)。当lk=0.22 nm时，QM-FJC模型拟合曲线与实验曲线的力值平均偏差最小(ΔF6=42.182 23 pN，如图11(c)所示)。将它们与实验曲线分别进行对比，如图11(b)和图11(d)所示，可以看出，无论是QM-FJC还是QM-FRC模型，都是在高力区可以重合，低力区不可以重合。这说明QM-WLC模型比较适合于描述单个解折叠蛋白质链的弹性行为，而QM-FRC和QM-FJC模型并不能够准确描述单个解折叠蛋白质链的本征弹性。

图9 不同轮廓长度的蛋白质单分子链在壬烷中获得的归一化后的力曲线

图10 蛋白质实验曲线与QM-WLC模型拟合曲线对比

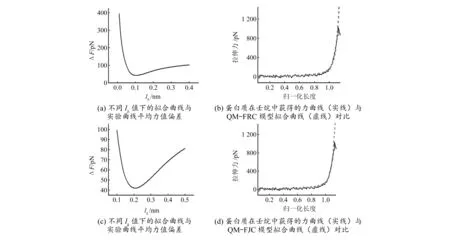
图11 蛋白质实验曲线与QM-FJC和QM-FRC模型拟合曲线对比

由于是在非极性有机溶剂中得到的力曲线，而且分子链与溶剂分子之间并没有明显的相互作用，仅仅存在范德华力的作用，因此其单分子力谱可以表征其本征弹性，所以此种拟合结果的差异应该归因于其分子链本身的分子结构。解折叠的蛋白质分子链内存在酰胺键，PLLA的分子链内存在酯键，由于酰胺键相对于酯键而言更加稳定一些，且链内旋转也受阻，因此可能会表现得更加刚性。QM-WLC模型是以WLC模型作为基础，可能更加适合描述较刚性一些的高分子的单链弹性行为，而QM-FJC和QM-FRC模型则更加适合描述较柔性一些的高分子的单链弹性行为。