无级变速装置的传动系统高精度控制设计

滑 娟，翟二宁

(1.咸阳职业技术学院机电学院，陕西 咸阳 712000)

(2.西北机电工程研究所四室，陕西 咸阳 712000)

传动系统是无级变速装置的关键组成，汽车的稳态行驶是依靠无级变速装置的传动系统完成的[1]。汽车发动机的转速与转矩主要通过无级变速装置进行调节，因此其行驶性能的优劣一定程度上取决于无级变速装置[2-3]。由此可知，改善无级变速装置中传动系统的控制精度，是提升汽车行驶性能的重要手段。目前，阈值控制是一种常用的边界控制方法，该方法的逻辑符合人脑思考过程，很好地解决了控制对象不确定的问题[4-5]，比较适用于非线性控制对象[6]，因此阈值控制方法在无级变速装置的传动系统控制方面得到了广泛应用。但是，一旦存在较大干扰，该方法很难确定准确的参数阈值。本文采用模糊控制方法添加参数自适应调整功能，设计参数自调整模糊-PI控制器(proportional integral controller)，以提升系统的控制精度为目标，通过探究无级变速装置结构可知，该结构自身存在的缺陷导致接触区产生自旋现象，影响传动系统精度，为此采用参数自调整模糊-PI控制方法，设计了模糊控制器以实现参数自调整。仿真结果证明，本文方法可实现对无级变速装置传动系统的高精度控制。

1 无级变速装置的传动系统高精度控制

1.1 无级变速装置相关参数计算

无级变速装置传动比i的方程为：

(1)

式中：ain，aout分别为动力输入与输出轴转速；ainM，aoutM分别为内、外摩擦轮转速；IinM，IoutM分别为内、外摩擦轮直径；rinZ，routZ分别为内、外圆锥滚轮工作直径。

无级变速装置内摩擦轮与内圆锥滚轮接触区、外摩擦轮与外圆锥滚轮接触区牵引系数比的计算方法如下：

(2)

式中：φout，φin分别为外摩擦轮与外圆锥滚轮接触区牵引油生成的牵引系数、内摩擦轮与内圆锥滚轮接触区牵引油生成的牵引系数。

由式(1)、(2)可得不同接触区域牵引系数与无级变速装置的传动比关系：

(3)

设置摩擦副接触表面速度差与卷吸速度的比为滚轮比，以探究无级变速装置的相对运动关系，滚轮比计算公式如下：

(4)

式中：eout为外摩擦副接触表面速度差与卷吸速度生成的滚轮系数；ein为内摩擦副接触表面速度差与卷吸速度生成的滚轮系数；Qout，ΔQout分别为外摩擦轮与外圆锥滚轮接触区的卷吸速度及两者速度差；Qin，ΔQin分别为内摩擦轮与内圆锥滚轮接触区的卷吸速度及两者速度差；cinZ，coutZ为内、外圆锥滚轮在接触区的线速度；cinM，coutM为内、外摩擦轮在接触区的线速度。

无级变速装置结构自身存在的缺陷导致接触区产生自旋现象，从而影响传动系统的精度[7-8]，内、外摩擦副接触区自旋表达式为：

gins=gzsinα=gouts

(5)

式中：gz，α分别为结构对应转速与对应半锥角；gins，gouts分别为摩擦副接触区的输入与输出。

为克服无级变速装置结构自身缺陷产生的接触区自旋现象，采用参数自调整模糊-PI控制方法设计控制器，以实现传动系统的高精度控制[9]。

1.2 参数自调整模糊-PI控制器设计

在计算出相关参数后，采用参数自调整模糊-PI控制方法提升传动系统控制精度，在考虑无级变速装置接触区中的内、外摩擦副接触区自旋的基础上构建模糊控制器。

通常误差与误差变化率是模糊控制器的输入量，则模糊控制器的输入变化量的表达式为：

Δu(t)=F[e(t),ec(t)]

(6)

式中：Δu(t)为模糊控制器的输入变化量；e(t)，ec(t)分别为误差与误差变化率；F表示映射关系,F[e(t),ec(t)]为误差与误差变化率的模糊映射关系；t为控制时间。

控制对象系统的输入表达式如下：

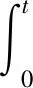
(7)

式中：u(t)为模糊控制器的输入量；Ku为比例因子。

采用离散方法构建传动系统控制器的表达式为：

Wu(t)=KuTF[e(t),ec(t)]

(8)

式中：Wu(t)为在一定控制时间t内的模糊控制输出；T为采样周期。

无级变速装置的传动系统处于平衡状态时，e(t)=0，u(t)=u0，其中u0为模糊控制量[10]。若使稳态误差控制在极小区域内，需令T值不变、Wu极小，然而这会导致无级变速装置的传动系统动态响应速度减缓、耗时较长。为解决该问题，对模糊控制器输出和控制对象添加比例项[11-13]，同时考虑无级变速装置接触区内、外摩擦副接触区自旋现象，进一步提升无级变速装置的传动系统控制精度，此时模糊控制器输出形式如下：

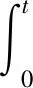
(9)

式中：Wl，WP分别为比例项增益量与积分项增益量。

在传动系统的动态与静态时期，输入量化因子We，Wec与输出比例因子存在差异，导致定值参数不能适应动态与静态的过程，获取的动态与静态特性不符合标准[14]。为了优化传动系统的模糊控制性能，需要调整控制器参数，参数的调整以传动系统误差与误差变化等数据为依据[15]，调整规则如下：若误差与误差变化较大，减小We，Wec值，增大Wl，WP值；若误差与误差变化较小，则执行相反操作。

设计的参数自调整模糊-PI控制器如图1所示。

图1 参数自调整模糊-PI控制器示意图

图1中模糊控制表是常规模糊控制器，输入模糊集合为e=ec={负(H),零(L),正(F)}，输出模糊集合为U={负大(HD),负小(HK),零(LO),正小(FK),正大(FD)}，输入与输出模糊变量归一化范围是[-1,1]。

参数自调整模糊-PI控制器依据模糊控制方法进行控制，参数调节器输入模糊变量集合为E=DE={负大(HD),负小(HK),零(LO),正小(FK),正大(FD)}，同样以[-1,1]作为归一化区间，将三角函数作为隶属度函数，放大倍数N的语言变量模糊集合为N={大放(GD),中放(GM),小放(GK),不变(BM),小缩(JK),中缩(JM),大缩(JD)}，设置N的论域为(1/8,1/4,1/2,1,2,4,8)。图2为模糊变量N的隶属度函数，表1为参数调整规则。

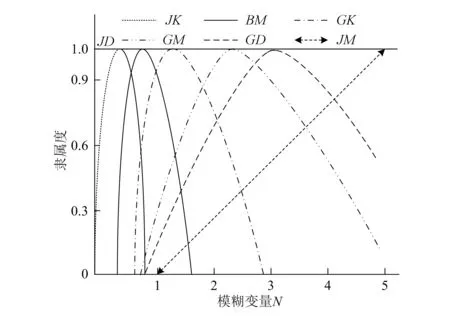
图2 模糊变量N的隶属度函数图

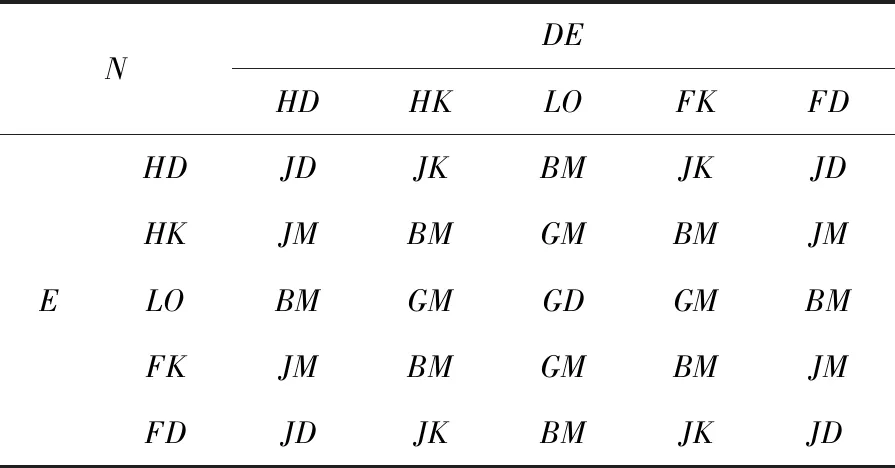
表1 参数调整规则表

2 测试与应用分析

2.1 测试参数设置

为验证参数自调整模糊-PI控制方法在无级变速装置传动系统控制方面的有效性，进行测试分析。通过仿真平台进行控制效果测试，定义起步、加速以及爬坡连续工况，将新型双锥无级变速装置作为实验对象，采用本文方法控制传动系统，得到的输入转矩与输出转矩关系如图3所示，传动系统主要参数见表2。实验对比控制方法为补偿控制方法、神经网络PID控制方法。

由图3可以看出，当输入转矩为150 N·m时，输出转矩为1 200 N·m；当输入转矩为1 350 N·m时，输出转矩出现峰值并稳定在2 900 N·m。输出转矩总体呈直线上升趋势，说明新型双锥无级变速装置的承载能力较强。

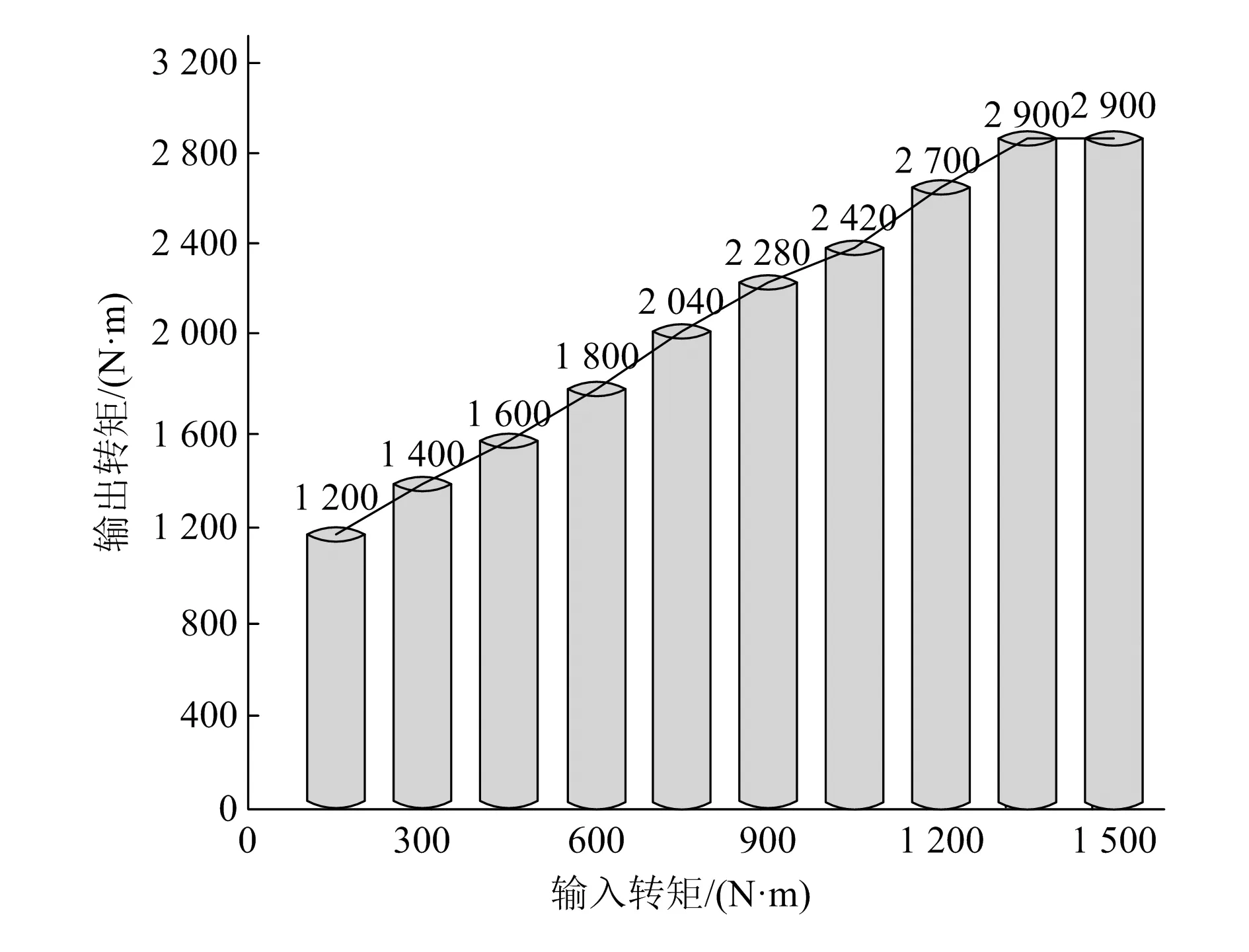
图3 新型双锥无级变速装置输入转矩与输出转矩关系

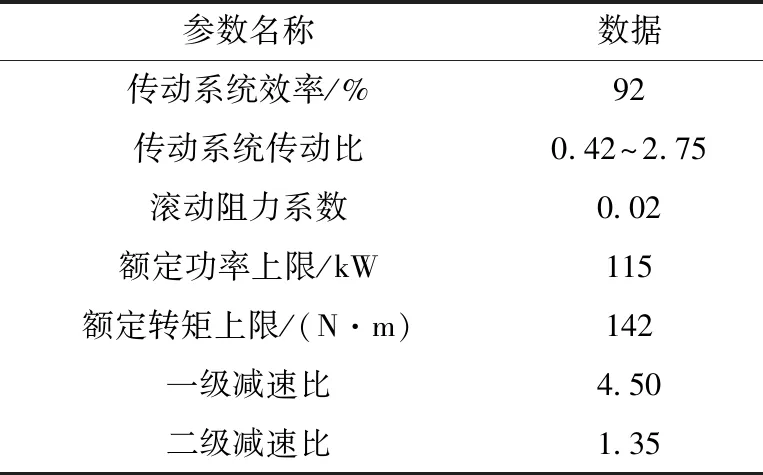
表2 无级变速装置传动系统主要参数

2.2 动力影响分析

从动力影响角度分析在不同方法控制下无级变速装置传动系统的性能，记录车辆等速行驶一定时长后加速过程的动态响应情况，如图4所示。

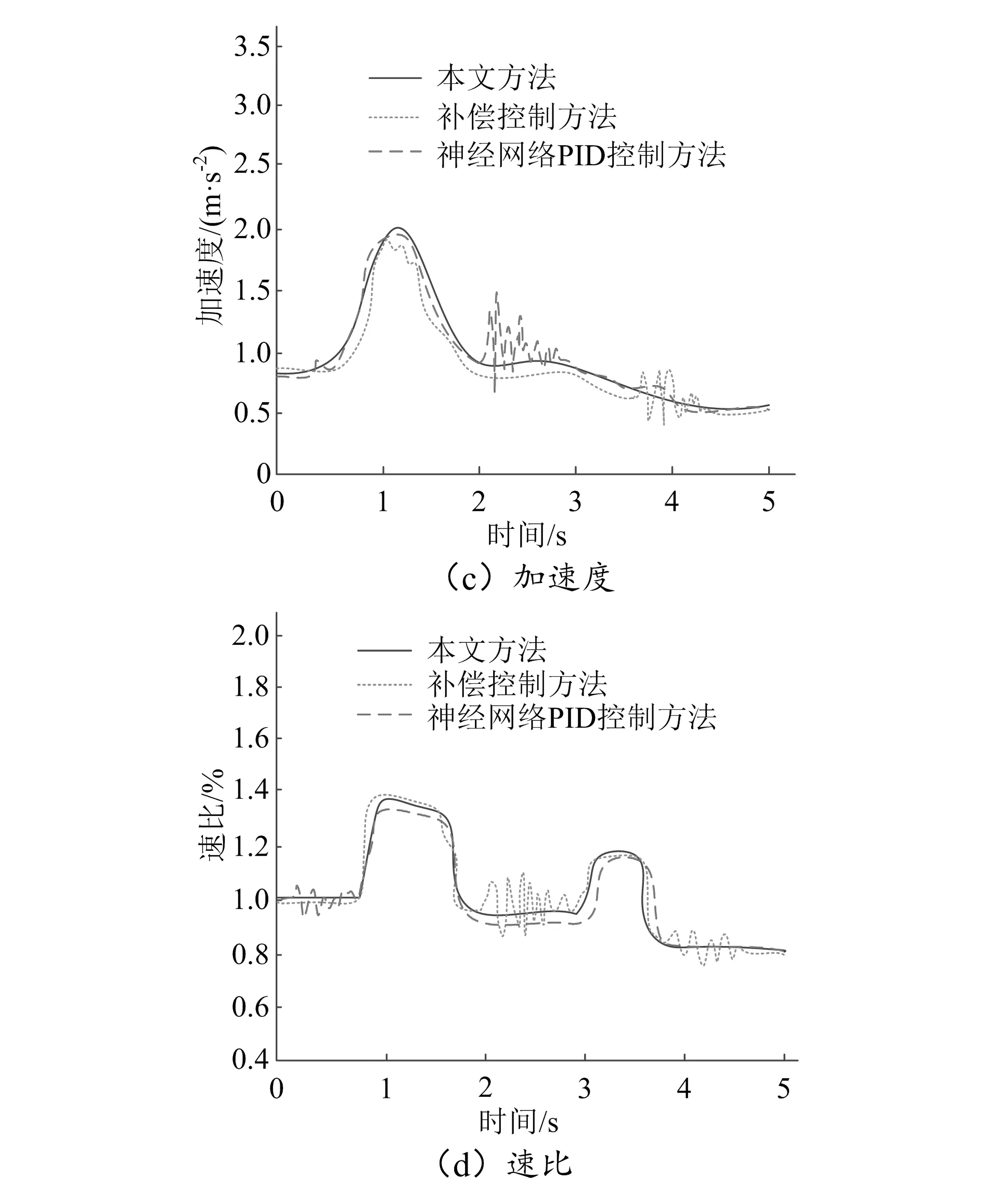
图4 不同方法控制下动态响应曲线

分析图4可知，在不同方法控制下，无级变速装置传动系统的动态响应曲线各不相同。补偿控制方法、神经网络PID控制方法的动力响应曲线均波动较大，补偿控制方法在速比响应曲线中表现显著，神经网络PID控制方法在车速、加速度响应曲线中表现显著，说明这两种方法在控制传动系统的过程中动力性变化大，控制效果较差。本文方法动力响应曲线均光滑、平缓，波动较为平稳，说明采用本文方法控制的传动系统动力性变化小，控制效果好、精度高。

2.3 传动比分析

3种方法在连续工况下的传动比跟踪结果如图5所示。

由图5可知，本文方法与目标传动比发展方向基本一致，重合度高，证明在本文方法控制下传动系统的传动比与目标值接近，传动性能优；相对而言，补偿控制方法、神经网络PID控制方法与目标传动比曲线走向差异大、贴合度较低，说明这两种方法控制的传动系统性能较差，由此突出采用本文方法控制无级变速装置传动系统的有效性与优势。

2.4 控制误差分析

为验证本文方法能够实现无级变速装置的传动系统高精度控制，并具有显著优势，进行6次不同工况的控制测试，工况分为起步、加速以及爬坡三阶段，难度相当，记录不同方法的控制误差，见表3。

图5 连续工况传动比跟踪结果

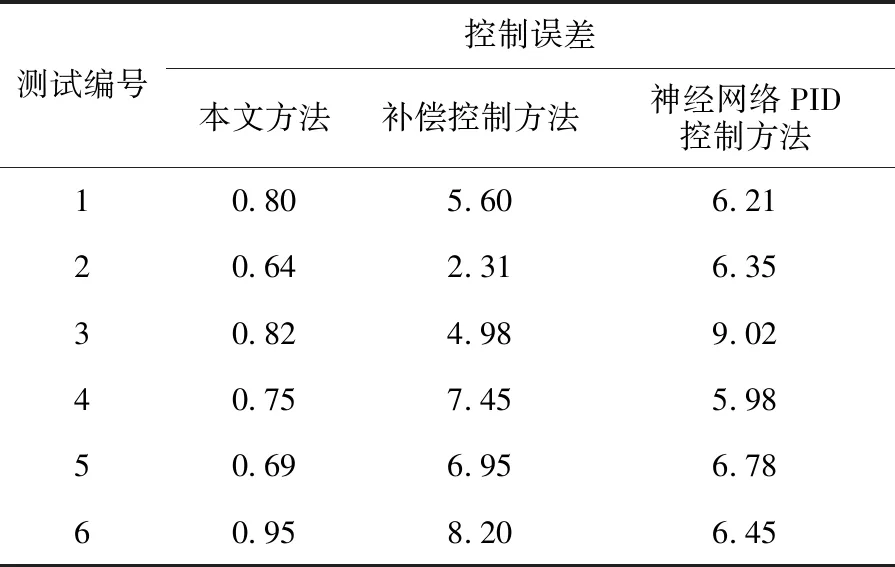
表3 不同方法的控制误差 %

由表3可知，本文方法控制误差均低于1%；补偿控制方法控制误差最高可达8.20%，在测试2中，控制误差最低为2.31%，但是大部分测试中控制误差仍然较高，不符合高精度控制标准；神经网络PID控制方法误差在5.98%～9.02%，同样不能实现高精度控制。根据上述分析结果可知，本文方法控制无级变速装置传动系统的误差小、精度高，符合高精度控制标准。

3 结束语

本文采用参数自调整模糊-PI控制方法设计模糊控制器，实现对无级变速装置中传动系统的高精度控制。常规模糊控制器控制精度较低的原因体现在两方面：一是未考虑无级变速装置结构自身缺点，导致内、外摩擦副接触区有自旋现象，控制精度低；二是常规控制器输入量化因子与输出比例因子在传动系统动态与静态时期存在差异，导致定值参数不能适应这两种状态，获取的动态与静态特性不符合标准，控制精度低。

本文从这两个角度出发提升传动系统控制精度，设计参数自调整模糊-PI控制器，依据参数调整规则表自调整参数，在起步、加速以及爬坡连续工况下进行仿真实验，结果证明本文方法符合无级变速装置的高精度设计需求，为无级变速装置传动系统高精度控制开发了新手段，同时为提升车辆承载力、保障车辆稳态行驶奠定了基础。