高压双动断路器冲击动力学仿真

刘亚培，王之军，杜迎乾，张 豪，张 博，郝相羽

(平高集团有限公司，河南 平顶山 467001)

作为电网系统中的控制保护执行设备，断路器的设计涵盖了机械、电、热、流体、电磁场以及自动控制等多个学科。对断路器机械性能的研究，常采用多体动力学方法来研究其传动系统的运动特性，由于把零件处理成刚体，忽略了结构的变形能，因此无法评估各个零件在冲击过程中的应力水平[1-2]。也有一些研究采用冲击动力学方法，但多集中在单独的传动机构[3-4]或弹簧机构[5]，鲜有对整机模型进行详细的仿真模拟，而且对于模型中次要的传动结构多进行了有限元模拟方式的简化，比如铰链采用1D梁单元进行模拟等，这种处理方式简化了建模和分析过程，但也忽略了传动副本身的变形。

本文采用LS-DYNA软件，旨在尝试建立断路器整机的详细仿真模型，同时考虑接触、摩擦引起的能量损失和各零件的弹性变形，研究各个结构的瞬态应力-时间曲线等冲击特性，最后通过试验验证了仿真方法的可行性和仿真结果的准确性。

1 仿真模型的建立

1.1 断路器结构介绍

高压双动断路器结构主要由弹簧机构和断路器本体两个子结构组成，其结构如图1所示。弹簧机构(图1左端)是高压双动断路器的动力来源；断路器本体传动系统(图1右端)将弹簧机构的动作传递到高压开关的触头上。

图1 断路器整机模型

区别于传统的动、静触头，灭弧室内的两侧触头都可以运动，通过触头联动实现合、分闸，即双动。双动结构(如图2所示)只需要较少的能量就可以得到单动结构同样的开断间距，因而更有利于降低弹簧机构的操作功，进而提高断路器的机械可靠性。

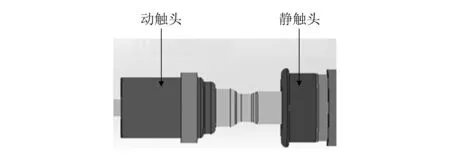
图2 双动触头

断路器合闸-分闸操作是一个涉及摩擦、间隙、碰撞、柔性等多因素的过程[6]。弹簧机构合闸-分闸结构示意图如图3所示。弹簧机构工作过程如下[7]。

合闸过程：合闸掣子在重力作用下转动，与锁扣分离，合闸弹簧释放能量，飞轮齿轮在合闸弹簧作用下转动，同时凸轮转动，带动合闸磙子转动，拐臂随之转动，同时拉动分闸链条，分闸链开始储能，拐臂通过内花键带动花键转动，拐臂转动的同时，缓冲器被拉开，合闸动作完成，分闸弹簧储能完毕。

分闸过程：分闸一级掣子松开，分闸二级掣子释放，分闸弹簧释放能量，花键、拐臂等在分闸弹簧作用下转动，实现分闸。分闸的同时，拐臂带动活塞杆运动，缓冲器将分闸能量缓冲掉。

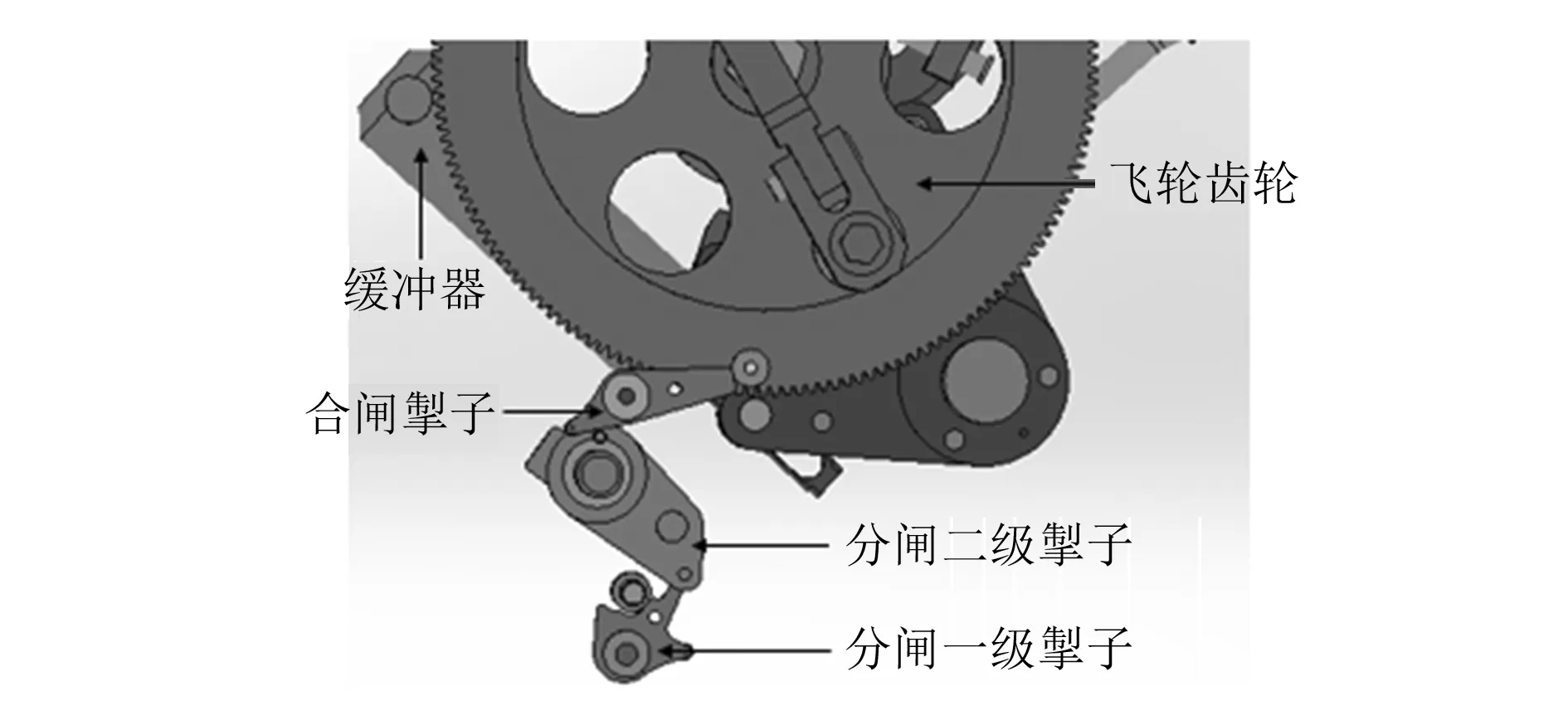
图3 弹簧机构结构示意图

断路器的合闸、分闸过程一般在几十毫秒以内，动作过程时间短、冲击大，属于典型的冲击问题。

1.2 网格划分

模型的前处理工作在Hypermesh中进行。综合考虑仿真精度和效率，整体网格尺寸控制在2～ 3 mm；为了相对精确地模拟接触，对于轴销类的柱面接触，接触面网格尺寸控制在1.5～2.0 mm，以减少由接触的数值模拟引起的接触面的初始间隙和轻微穿透对结果的影响；对于单元类型，总体上采用精度较高的线性六面体单元进行网格划分，对于个别的难以进行六面体网格划分的结构，如动端固定座等，采用四面体单元进行网格划分。断路器的整体网格模型如图4所示，共划分2 040 000个单元，2 070 000个节点。

图4 断路器网格模型

1.3 分析设置

高压断路器的机械可靠性要求材料在弹性范围内工作，因此材料模型不考虑塑性。针对仿真涉及的材料，分别定义其密度、弹性模量和泊松比3个物理量。

接触采用LS-DYNA软件中适应性较好的自动接触，软件的关键字为*contact_automatic_single_surface。

时间步长(time step)设置为2E-07 s，计算的终止时间(termination time)为180 ms。采用高级质量缩放功能，将最小稳定时间步长增大至2E-07 s，从而提高计算效率。在16核工作站上执行一次完整分析需要50 h。后续仿真结果表明，质量缩放引起的动能增加占总能量的百分比小于1%，满足精度要求。

1.4 仿真结果

连杆作为双动断路器结构的关键传动零部件，根据以往的产品开发经验，应重点关注连杆处的应力分布。连杆处的Mises应力峰值出现在分闸过程中，应力峰值为568 MPa，如图5所示。连杆的材料为35CrMo，经过热处理工艺，其屈服极限为913 MPa。

图5 应力结果

2 试验介绍

仿真模型上的连杆标号如图6所示，试验样机贴片位置如图7所示，测试采样频率为10 kHz，采用测试软件自带的巴特沃斯滤波器进行数据处理。参数设置如下：低截止频率1 000 Hz、高截止频率2 000 Hz、阶数5、通带波动0.1 dB、阻带衰减120 dB。

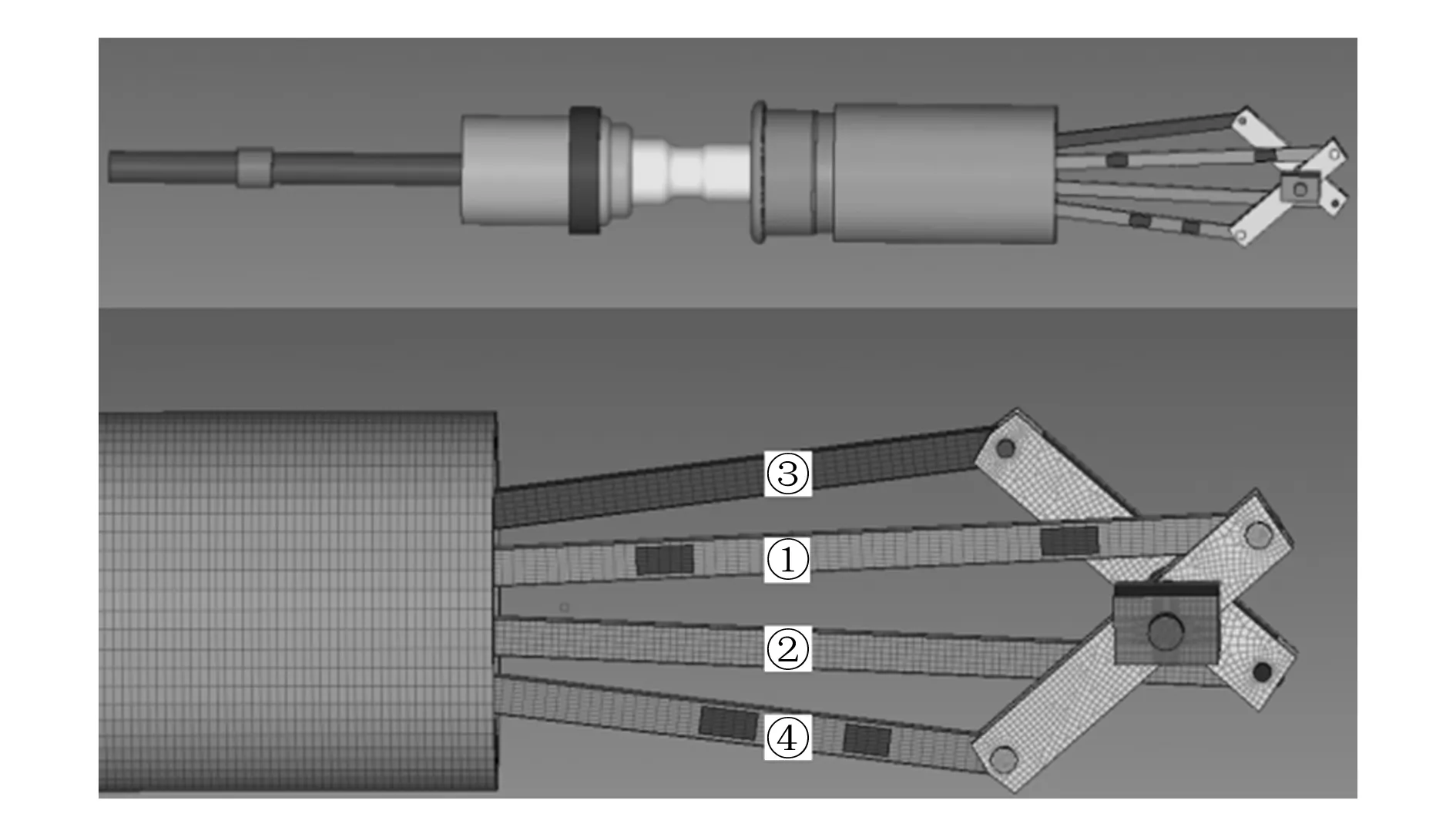
图6 仿真模型的应力提取位置

为了更准确地提取仿真模型上测点位置的表面应力，与试验数据进行对比，在网格模型上的测点位置建立膜单元，膜单元厚度为1E-06 mm，保证其不会对原结构力学性能产生影响，膜单元应力结果输出时间间隔为1 ms，应力-时间曲线未做滤波处理。

图7 应变片位置

3 对标与分析

整体模型的高应力区域出现在连杆位置，其中3号和4号杆的应力要高于1号和2号杆，符合以往的产品开发经验。仿真和试验结果都表明，分闸过程的应力峰值要高于合闸过程，因此重点比对了分闸过程3号杆上部(图8)、3号杆中部(图9)和4号杆上部(图10)的仿真结果和试验结果。

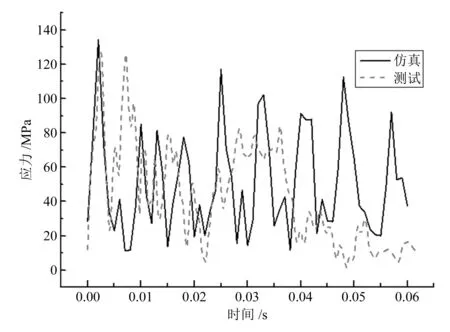
图8 3号杆上部应力结果

图9 3号杆中部应力结果

仿真模型的峰值应力出现在3号杆上部，为134.38 MPa，此处实验测量的应力峰值为125.89MPa，相对误差为6.74%；其他测点的应力峰值和相对误差见表1。

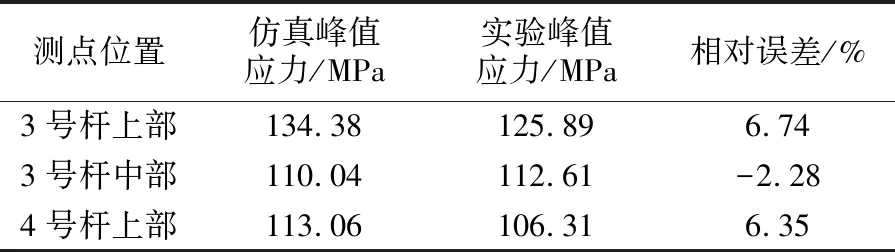
表1 应力结果对标

影响仿真应力结果精度的因素有很多，比如计算方法、网格密度、模型简化等：

1)受显式计算方法所限，仿真模型的单元类型为一阶六面体单元，相对于高阶单元，同样的网格密度，一阶单元的精度较低，而二阶全积分单元虽然精度高，但会大大增加计算成本，目前主流的显式计算方法并不支持高阶单元。

2)网格的密度是影响求解精度的主要因素。尤其对于接触面处的网格，由于有限元网格离散导致接触部位不可避免地会出现一些“尖点”接触，甚至穿透，导致结果的震荡，尤其在轴销类等曲面接触中，会导致接触应力显著增大；如果关注接触面上的应力，则需要进一步细化网格。本文模型主要考虑求解效率，对接触面的网格仅进行了少量的细化，网格尺寸为1.5 mm。

3)曲线出现偏差主要是由于在能量的传递过程中，仿真模型未能精确地体现物理样机，比如在弹簧储蓄能量和释放能量的过程中，将弹簧模型简化为1D弹簧单元，可能会引起弹簧能量的损失。由于断路器整机结构的复杂性，很难建立考虑全面细节的仿真模型，这在很大程度上(尤其是弹簧机构的模拟)导致了能量的传递与时间的曲线存在一定的偏差。

4)摩擦系数根据材料的表面处理方式指定，可能与真实的摩擦系数有一定的偏差，这对于仿真结果会有一定的影响。

4 结束语

本文建立了高压双动断路器瞬态冲击动力学的仿真模型，提出了零件的单元尺寸设置、网格划分方法、接触模拟方法等模型建立方法，为今后同类型产品的冲击仿真模型的快速搭建提供参考；通过试验对比，验证了仿真模型和仿真方法的合理性。由图8可知：高应力区域应力峰值吻合度较好，最大相对误差为6.74%；仿真与试验的应力结果显示，曲线形状吻合度有一定的偏差，主要原因在于仿真模型过于复杂，而冲击动力学仿真涉及碰撞、摩擦、间隙、柔性等诸多因素，从而大大增加了仿真模型中应变传递的不确定性。