厦门岛海岸线分形特性演变规律的研究

林 松俞晓牮庄小冰李焱龙张 宇赵志庆

(1.厦门大学 海洋与地球学院,福建 厦门361005；2.闽南师范大学 生物科学与技术学院,福建 漳州363000；3.哈尔滨工业大学 建筑学院 寒地城乡人居环境科学与技术工业和信息化部重点实验室,黑龙江 哈尔滨150001；4.厦门大学 建筑与土木工程学院,福建 厦门361005)

海岸带是海洋与陆地系统交叉作用、相互影响的地理单元,是研究滨海城市发展的重要平台,海岸线是海岸带与海洋边界的重要标识,人们常以多年平均大潮高潮时的水陆分界痕迹线来指代海岸线。海岸带的环境变化会影响海岸线的空间形态,研究海岸线的变迁对海岸带环境演变研究具有重要意义[1]。近年来,港口建设、填海造陆等海岸带经济开发活动日益频繁,数据表明[2],仅在1979—2014年,中国的填海造地面积就高达2 156.77 km2,严重改变了海岸带的生态环境,加剧了海岸线的变迁过程。因此,监测海岸线变化反映海岸带的动态过程,对于制定填海造陆、港口开发等海洋工程规划具有重大意义。

海岸线具有多重的凹凸复杂结构[3],它是典型的、具有自相似特性的系统,不能简单地用点、线、面等整维数的几何体来描述。1967年,Mandelbrot[4]研究英国海岸线中首次引入了海岸线分形的概念,并在后续研究中运用量规法模拟计算出包括英国、法国以及非洲等一系列区域海岸线的分形维数为1.2～1.3[5]。之后几十年,海岸线的分形理论逐渐发展成熟,不再局限于分形维数的模拟计算,而是利用遥感影像来计算海岸线的实际分形维数,运用的计算方法包括改进的量规法[6-8]、谱分析法[6]和盒子计数法[8-10]等。当前,国内外已有较多应用分形理论分析海岸线变迁的研究,例如:Jiang采用改进的量规法,分割计算了美国各海岸弧的分形维数,发现美国的大西洋海岸的分形维数要比太平洋海岸高得多,并将计算结果与海岸线复杂程度相联系,解释了沿海物种分布和多样性模式[7]；叶晓敏基于遥感数据,采用盒子计数法,计算了胶州湾[10]和渤海湾[11]历史岸线的分形维数,并分析了其演变特性,发现海湾岸线变迁的主要驱动因素是养殖场建造、围填海和港口建设等。可见,分形理论是描述海岸线几何特征有效工具之一,可以为滨海城市海岸线的复杂性演变研究提供重要的定量分析手段。

厦门岛是厦门经济特区的发祥地,是东南沿海地区经济发展最快速的区域之一。快速的城市化进程使得厦门岛的自然海岸几乎完全被人工海岸所取代,并且由于大规模的填海工程,岛屿面积从最初的110.80 km2,扩展到157.76 km2[12],这使得厦门岛海岸线的复杂程度大大降低。由此可见,厦门岛海岸线的变迁和岛屿的城市化进程存在一定的内在关系,通过对厦门岛海岸线分形特性演变规律的研究,能够反映厦门岛海岸带和海岸环境的变动,为岛屿的市政与海洋工程规划提供一定的参考。

选取厦门岛为案例区,利用1976—2018年厦门岛海岸带的Landsat卫星图像资料,结合改进的归一化水体指数(Modified Normalized Difference Water Index,MNDWI)和基于Canny算子的边缘检测法,以数字图像处理方式,提取研究期间厦门岛的海岸线图像。然后,根据提取出的海岸线图像,计算出各年间厦门岛海岸线的分形维数并分析其演变规律。最后结合研究期间厦门岛的填海造陆规划,探讨厦门岛海岸线变迁与其分形特性演变之间的内在关系。

1 研究区域与研究方法

1.1 研究区域概况

厦门岛(118°02'～118°13'E,24°25'～24°33'N),隶属于福建省厦门市,位于福建南部的海湾、九龙江口外侧,岛屿土地总面积约157.76 km2,它是典型的人口高度集中和经济高度发展的滨海区域,目前岛上已经高度城市化。由于海峡西岸经济区的建设,厦门岛经历过多次海洋工程,目前岛屿的淤泥质海岸出现严重退化。所以,厦门岛的海岸类型以人工海岸和基岩海岸为主,还保留少部分砂质海岸。

1.2 数据来源

数据来源于Landsat 2和Landsat 3卫星多波段扫描仪(Multi Spectral Scanner,MSS)影像、Landsat 5卫星主题成像仪(Thematic Mapper,TM)影像、Landsat 8卫星陆地成像仪(operational land imager,OLI)影像[13]。MSS影像数据包含4个波段(绿色、红色、波长不同的2个近红外波段),所有波段的分辨率均为60 m。TM影像数据包含7个波段(蓝色、绿色、红色、近红外、波长不同的2个中红外和热红外波段),其中,热红外波段的空间分辨率为120 m,其余波段空间分辨率为30 m。OLI影像数据在TM影像数据的基础上增加了气溶胶(分辨率为30 m)、全色(分辨率为15 m)和卷云(分辨率为30 m)波段,此外还缩小了近红外波段的波长范围。

为保证海岸线提取的精确性,我们对原始数据做了初步的筛选,以确保所研究的卫星影像中厦门岛的海岸带附近无云层覆盖,并且成像时间接近于当日的高潮时,因为高潮时岛屿的潮间带大部分或全部被海水覆盖,能较好地反映海岸线的信息。经过筛选,我们选取1976年和1981年的MSS影像,1987年、1995年、2000年、2005年和2010年的TM影像以及2015年和2018年的OLI影像作为研究对象(图1)。之后,对满足条件的卫星影像数据做系统辐射校正和大气校正,并且通过数字高程模型(Digital Elevation Model,DEM)进行地形校正,目的是消除大气、太阳高度角、视角和地形等对地面光谱反射信号的影响,以确保所提取的海岸线的精确度[12]。

图1 1976—2018年厦门岛卫星图像以及海岸线提取结果Fig.1 Satellite image and coastline extraction results of Xiamen Island from 1976 to 2018

2.3 研究方法

2.3.1 海岸线的提取方法

20世纪初,航空遥感技术的高速发展降低了实时获取高精度、大面积的海岸带影像的难度,促进了利用遥感影像提取海岸线技术的成熟。在这个时期,科研人员提出了三类提取海岸线的方法:1)简单利用水体和陆地图像灰度值差异或者根据水陆边界灰度值梯度值提取海岸线,例如神经网络分类器法[14]、边界跟踪法、基于小波变换和Snake算子边缘检测法等[15]；2)将卫星不同波段图像叠加成红-绿-蓝三原色(RGB)图后,增强水陆边界色彩差异性后提取海岸线,例如边界直方图法与波段组合法[14]；3)对原始图像做模糊增强变换,得到模糊特征数据,再映射回原始图像上,增强边界差异性的基于模糊信息处理的边缘检测法[16]等。在这三类方法中,边缘检测法因算法简单,能直接获取边界图像,使用率最高,但是对于水陆边界差异性不明显的遥感影像,该方法提取的海岸线精度却不高；波段组合法虽然能够增强水陆边界差异性,提高提取精度,但不能直接获取海岸线图像。因此,本研究先利用波段组合法中的常用的归一化水体指数(Normalized Difference Water Index,NDWI)或改进的归一化水体指数(MNDWI)对原始卫星影像做预处理,以提高水陆边界灰度级梯度,再进行基于Canny算子的边缘检测,以能够高精度地提取厦门岛在各年份厦门岛高潮时的水边线。高潮时,岛屿的水边线可以近似看作与岸线位置一致,因此在后续的计算分析中,我们用高潮时的水边线代替海岸线计算分析分形维数,这相较于传统的、通过历年的地图和海图来直接提取高潮时的水边线具有实时性、精度高、针对性和可自动化处理等优势(下文所提及的海岸线,均为高潮时的水边线)。

归一化水体指数(NDWI)是Mc Feeters提出的一种利用不同地类在不同波段中的波谱特点,利用比值计算快速提取水体信息的方法[17],NDWI定义公式为式中:RGREEN为影像中不同地类在绿光波段的反射率,RNIR为在近红外波段的反射率。

经过NDWI计算可以降低影像中植被、土壤的灰度级,将其与灰度级较高的水体区分开,但是在很多情况下,用NDWI提取的水体信息中仍然夹杂着较多非水体信息,特别是在提取人工地类与周边水体方面效果很差。因此,为了更好地提取人工地类中的水体信息,徐涵秋将NDWI公式中不同地类在近红外波段的反射率替换为在中红外波段的反射率,提出了改进的归一化水体指数(MNDWI)[18],MNDWI的定义公式为

式中:RMIR代表影像中不同地类在中红外波段的反射率。经过MNDWI计算,不仅降低了影像中植被、土壤的灰度级,还降低了影像中人工地类、阴影的灰度值,因此能更好地将人工海岸和水体区分开。

在研究中采用MNDWI对TM与OLI影像进行预处理,采用NDWI对MSS影像进行预处理,这是由于MSS影像中没有中红外波段。将经过预处理后的卫星图像导入编写的Canny边缘检测程序[19],边缘检测程序的思路是采用多路径检测,计算图像上每一点的梯度和边缘方向,根据边缘点在梯度方向上强度最大的特点,将所有的边缘点提取出来,连接边缘点后就可以得到高精度的厦门岛的海岸线。采用MNDWI或NDWI和Canny算子相结合的方法提取的海岸线和岛屿的轮廓线贴合程度高,能较大程度地保留海岸线信息。

2.3.2 分形维数的计算方法

盒维数是一种被广泛应用的分形维数,在分形理论的应用研究中被提出的许多维数的概念都是盒维数的变形,并且由于盒维数是由相同形状集的覆盖确定的,可以进行程序化的计算,因此研究中将厦门岛海岸线的盒维数作为分析的对象。

盒维数的计算方法就是使用不同边长的正方形盒子去覆盖待测海岸线图像,当正方形盒子的边长l发生变化时,包含海岸线图形的盒子数目N(l)也会发生变化,根据分形理论[3],N(l)∝l-D,对公式两边同时取对数,可以得到:

式中:C为待定系数,D为待测海岸线的盒维数。取不同边长的盒子去覆盖海岸线图像,得到对应的N(l)值,再开展拟合分析,即可得到盒维数D。为实现盒维数的计算,本研究编写了相关的Matlab软件程序,程序计算的具体过程为:1)对海岸线图像进行背景扩充,使图像的长宽相等；2)对扩充完的图像进行二值化处理,使得海岸线在图中显示为黑色,在相应的图像矩阵中表示为0；3)用行数和列数均为l的矩阵对海岸线图像进行盒子覆盖,得到一系列覆盖盒子数,即包含海岸线图像点(像素点为0)的盒子数和盒子大小的数据对(N(l),1/l)；4)将所有数据绘制在双对数坐标系中,并进行线性回归分析,如能得到一条拟合直线,则输出拟合直线的斜率以及拟合优度R2,拟合直线的斜率即为海岸线的盒维数。

为在保证足够的数据量的同时降低程序的运算量,研究中设计了一个递增的盒子大小的序列(l0=0):

为了验证分形维数计算程序的准确性,对已知分形维数的几何图形(圆形、Koch曲线、Apollonian垫片等)与经典海岸线(挪威海岸线、英国海岸线)的盒维数进行了计算和比较(表1),结果表明:对于圆这一类细节较少、分形维数为1的平滑曲线,其相对误差仅为0.21%,而对于Koch曲线、Vicsek分形和Sierpinski三角等具有较多细节的分形图形,相对误差略大一些,这是由于分形图形具有无限的细节,而所使用的图片分辨率是有限的,无法展示分形图形的所有细节,为计算结果带来了一定的误差。但总体来看研究中所设计的程序,无论对经典分形图形还是对经典海岸线分形维数的计算,相对误差均低于5%,具有较高的精度。

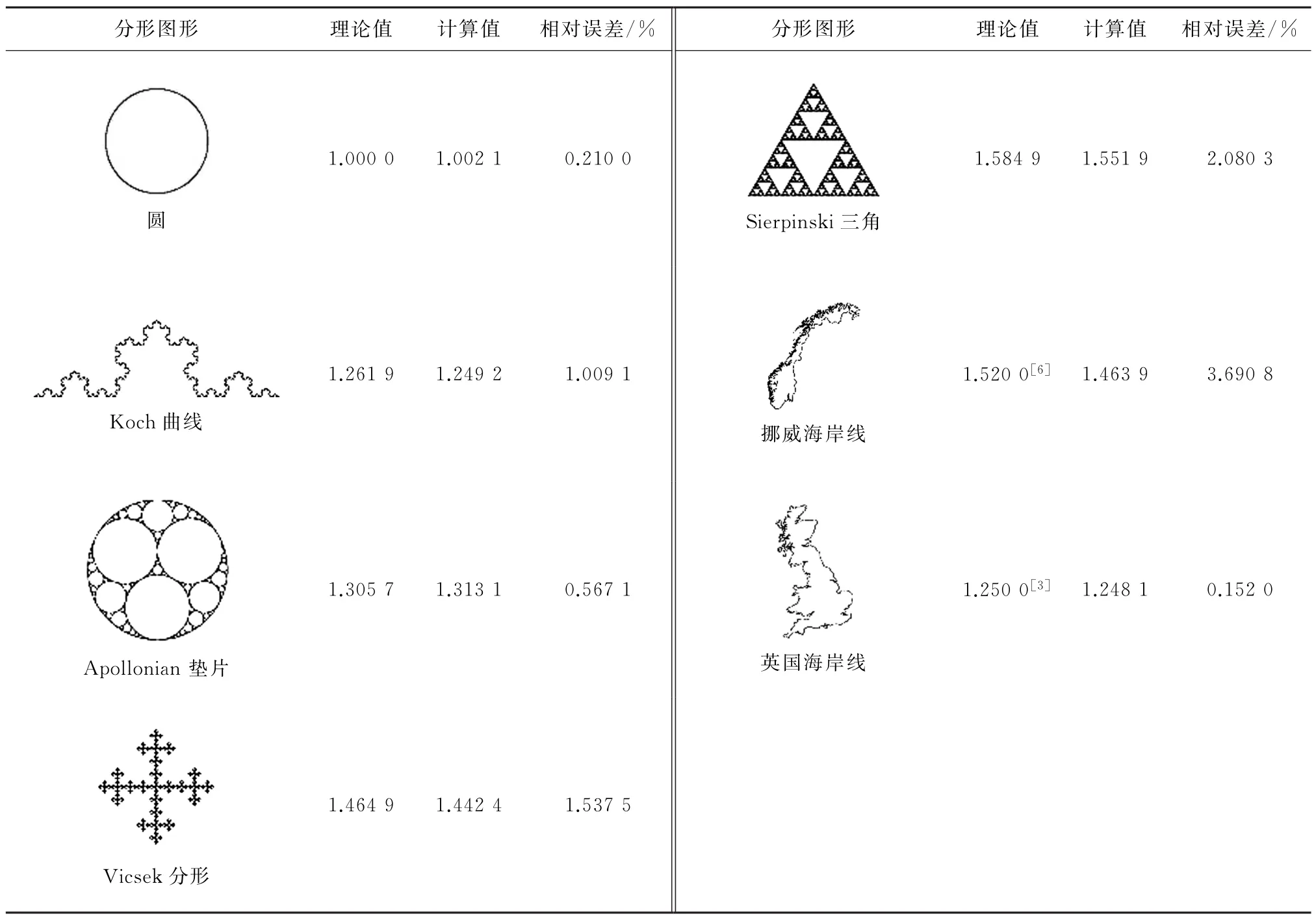
表1 分形图形盒维数计算结果Table 1 Fractal dimension of fractal images

3 结果与分析

3.1 厦门岛海岸线提取结果

从通过Canny边缘检测程序提取的1976—2018年厦门岛海岸线结果(图1)可以明显地看出:厦门岛海岸线具有不规则性和复杂性,这类似于经典的分形海岸线(如英国、挪威等)[4,7]；厦门岛海岸线表现了一定程度上整体与局部的空间相似性,这种自相似是分形的重要特性,因而可以用分形理论来描述厦门岛复杂海岸线。

从提取效果来看,对于基岩和人工海岸,采用MNDWI(NDWI)和Canny算子相结合的方法提取的海岸线基本贴合岛屿轮廓,但是对于砂质和淤泥质海岸,提取的结果和岛屿轮廓会有所偏差。以2018年厦门岛卫星图像数据的海岸线提取结果(图2)为例:对于岛屿北部人工海岸,所提取的海岸线基本贴合海岸轮廓；但是对与岛屿东南部的沙滩,仍有小部分海岸线没能完全贴合海岸轮廓,这是因为砂质海岸边缘灰度值梯度小,边缘探测精度不够高[20]。厦门经济发展带来的高度城市化使得岛屿的砂质、淤泥质海岸退化严重,进而致使整座岛屿以基岩、人工海岸为主,因此,从整体来看,所提取出的海岸线基本贴合整座岛屿,对厦门岛盒维数的计算与分形特性演变规律分析影响不大。

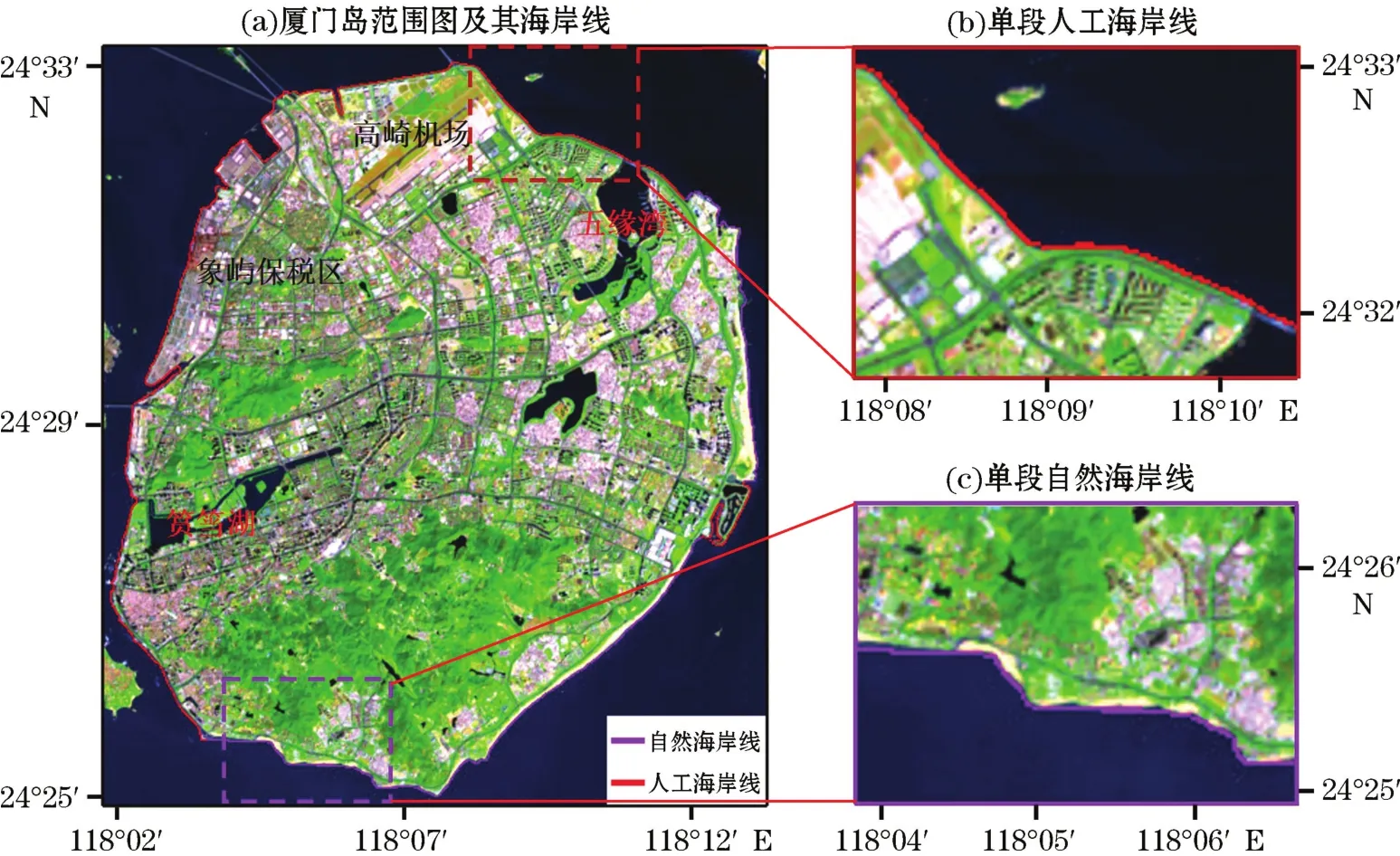
图2 2018年厦门岛人工海岸线 (岛屿北部)与砂质海岸线 (岛屿南部)提取效果对比Fig.2 Comparison of the extracted coastline along the artificial coast(northern island)and sandy coast(southeastern island)of the Xiamen Island in 2018

3.2 厦门岛海岸线分形特性

分形维数计算程序计算了厦门岛1976—2018年海岸线的盒维数值(表2),发现其历史海岸线的盒维数为1.098 9～1.118 1。可以看出,由于厦门岛历史海岸线复杂程度的不同,计算出的盒维数也不同。其中,厦门岛在1976年的海岸线盒维数值最大,而在2010年的海岸线盒维数值最小,结合厦门岛在这2个时期的海岸线图像(图1a和图1g),相比于2010年,1976年的厦门岛的存在大量的海湾,海岸线显得更加复杂,由此可见盒维数的大小和海岸线的复杂程度有关,海岸线复杂的岛屿的盒维数较大,海岸线简单的岛屿的盒维数较小。此外,由表2可知lnN(l)与的拟合优度均在0.997 9以上,可见厦门岛各个时期海岸线的分形特性是客观存在的。综上所述,分形维数可以作为表征厦门岛海岸线随时间变化的特征参数。

表2 1976—2018年厦门岛海岸线盒维数和拟合度Table 2 Fractal dimension of coastline of the Xiamen Island from 1976 to 2018

根据表2的结果,绘制出厦门岛海岸线1976—2018年间的盒维数演变曲线(图3),结合表2和图3的结果,可以看出,厦门岛海岸线的盒维数总体呈下降趋势。其中,1976—1981年,厦门岛海岸线盒维数呈现出急剧降低的趋势,仅在5 a间,盒维数下降了12‰；1981—1995年盒维数呈现升高的趋势,在14 a间增加了8.95‰；在1995—2010年盒维数呈现快速降低趋势,在15 a间下降了13.23‰；而2010—2018年,盒维数不再有大幅度的变化,变化幅度都在1.4‰以内。

由于海岸线的盒维数与其复杂程度有关,本研究根据海岸线提取结果绘制了1976—2010年厦门岛海岸线变迁图(图4),分阶段探讨厦门岛海岸线盒维数变迁的原因。

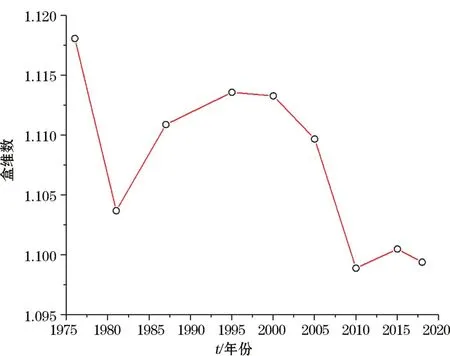
图3 1976—2018年间厦门岛海岸线盒维数的变化Fig.3 Box dimension variability of the Xiamen Island from 1976 to 2018

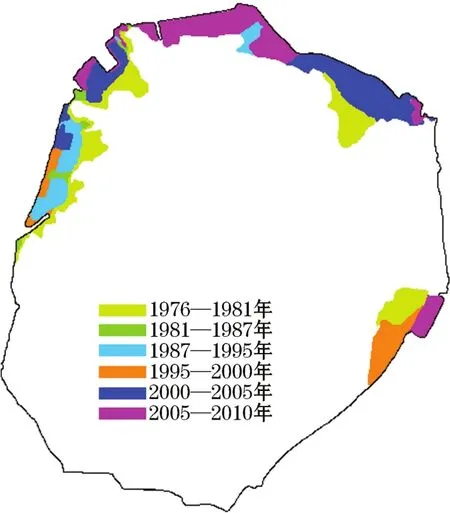
图4 厦门岛1976—2010年海岸线变迁阶段图Fig.4 Stage map of coastline changes in the Xiamen Island from 1976 to 2010

1)1976—1981年,厦门岛海岸线盒维数急剧下降,从1.118 1降低至1.103 7,这主要是因为岛屿西北部象屿保税区的大规模填海工程使得西北部的天然海湾大量消失,弯曲的岸线变得平直,直接导致盒维数的降低。此外,岛屿东部的填海造田工程,也降低了厦门岛东岸的海岸线的复杂程度,从而使总的海岸线盒维数减小。

2)1981—2000年,厦门岛海岸线盒维数出现较大幅度的增加,从1.103 7增加至1.113 3。在此期间,厦门岛的填海工程依旧集中在岛屿西北部的象屿保税区,在原有的基础上向外扩建,此外还修建了码头与港口,造成了人工海岸线的增加,提高了海岸线的复杂弯曲程度,造成了海岸线盒维数的上升。

3)2000—2010年,厦门岛海岸线盒维数再次急剧下降,从1.113 3降低至1.098 9。在此期间,岛屿北部的五缘湾地区进行了大型的填海工程,使得北海岸的岸线复杂程度大大降低,导致了盒维数的下降。值得注意的是:2005—2010年厦门岛的海岸线盒维数急剧降低,5年间下降了9.73‰,这主要是因为高崎机场的建成,使得原本曲折不平的自然海岸线变成了平直的人工海岸线,大大降低了海岸线的复杂程度,从而使总的海岸线的盒维数急剧降低。

4)2010—2018年,厦门岛海岸线的盒维数变化开始变得缓慢,在1.100 0左右波动。盒维数的变化主要是自然过程造成的,例如五缘湾的泥沙淤积、海水侵蚀等。

由此可见,填海造陆工程是影响海岸线盒维数的最主要原因。通过分析不同年份之间的盒维数的变化,我们就可以评估填海工程对海岸线复杂程度以及海岸带的影响。一般情况下,只要在研究期间出现了盒维数的大幅下降,就意味着这一时期填海工程的主要区域为海湾地带,使得海岸线变得平直；而在研究期间出现盒维数的上升,则说明这一时期的填海工程主要是为了建设新的码头或者港口,使得海岸线变得复杂。

对于整个厦门岛来说,1976—2018年,其整体海岸线分形维数呈总体下降的趋势,这说明期间对海岸线的填海工程使得厦门岛的整体海岸线趋于平直。而若将厦门岛海岸线二等分,可以发现其填海工程主要集中在岛屿的西北部,而南部在1976年以后几乎没有很大的开发计划,这种明显的对海岸线的填海工程的空间分布特征非常值得对海岸线分段并做进一步的分形分析。

4 结 论

本研究提出基于卫星遥感影像的厦门岛海岸线分形维数分析方法,获得了厦门岛1976—2018年的海岸线盒维数,在此期间,厦门岛海岸线的盒维数先后经历了急剧降低(1976—1981年),增加(1981—2000年),再迅速降低(2000—2010年),最后缓变(2010—2018年)四个阶段。分析表明,填海造陆工程是导致厦门岛海岸线分形特性变化的主要原因,盒维数的变化大小,直接反映了填海造陆工程对厦门岛自然海岸线的人为改造程度。滨海城市发展过程中,海岸线空间形态的分形定量研究有重要的理论和实践意义。对海岸线进行分形量化分析,能估计海岸线的具体变动,预估人类活动对海岸带生态环境所带来的影响,给海岸带资源开发、生态保护以及城市规划提供参考依据。

致谢：南京大学物理学院硕士研究生林懿然和厦门大学海洋地球学院工程师徐晓辉分别在盒维数算法和遥感数据处理方面提供了帮助。