青岛外海潮致第二模内孤立波的观测研究
2020-04-01杨光兵郭延良于龙陈
杨光兵郭延良于 龙陈 亮
(1.自然资源部第一海洋研究所 海洋环境与数值模拟研究室,山东 青岛266061;2.青岛海洋科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室,山东 青岛266237;3.中国海洋大学 海洋与大气学院,山东 青岛266100)
内孤立波经常能够在具有密度层结的流体中观测到[1-4],它能够引起等密面的剧烈起伏[5]并造成强烈的湍流混合[6-7]。其中,第一模内孤立波的出现几率更高,在两层流体中,如果上层较薄,这种内孤立波会使等密面下陷,形成下陷波;反之,在下层较薄时,这种内孤立波会使等密面上凸,形成上凸波。和第一模内孤立波相比,针对第二模内孤立波的研究[8],特别是观测研究,相对较少。第二模内孤立波出现在三层流体中,外凸型第二模内孤立波使上层等密面上凸并使下层的等密面下陷;另外一种内凹型第二模内孤立波则使上层等密面下陷并使下层等密面上凸。观测显示,虽然第二模内孤立波的能量只有第一模内孤立波的1%到1/10,但由于第二模内孤立波具有更复杂的垂直结构,它引起的湍流混合和第一模内孤立波接近[9],因而第二模内孤立波对海洋混合同样具有重要作用。根据此前的研究结果,主要的第二模内孤立波的生成机制包括[4,10]:1)第一模内孤立波向岸传播并进入破碎不稳定阶段(模式和实验室实验结果)[11];2)第一模内孤立波流经海底山(观测结果)[12-13];3)重力流头侵入三层流体(实验室结果)[14];4)流经负地形并且主跃层位于中部时(模式结果)[15];5)第一模内孤立波的反射(观测结果)[16];6)内潮模的非线性瓦解(模式结果)[17];7)内潮波束从密跃层下方的照射(模式结果)[18];8)Lee波机制(观测结果)[19]。这些结果更多来自模式研究,并且在第二模内孤立波生成过程中,局地层结状态基本保持稳定。
青岛近海海域为南黄海的一部分。在夏天,黄海的最重要水文特征即为黄海冷水团[20]。黄海冷水团是一个海盆尺度的低温水体并位于季节性跃层之下。它在前一个冬天受表层降温和强烈垂直混合作用而在局地形成。由于黄海冷水团的存在,夏季黄海的主要水文特征即为强温跃层和强温度锋面。在这种水文条件下,青岛附近海域的内波活动获得了较多的研究关注并有较长的观测历史,郑全安等率先利用机载雷达图片研究了青岛附近海域的内孤立波[21],在2012年于青岛附近海域针对内波开展了2次现场观测,分别观测到了涨潮对第一模内孤立波极性变换的影响[22]以及台风通过改变层结对内波的影响[23-24]。
本文利用于2013年夏季在青岛附近海域开展的现场观测展开研究,结合温度链、CTD、ADCP等设备获得的观测资料,报道海区内的第二模内孤立波现象,并结合Kd V方程探讨所观测到的第二模内孤立波的产生机制。
1 现场观测
现场观测开展于2013-08-29。图1所示为观测站点位置、海区地形以及海区底层温度分布,由图可见观测站点(120°39'30″E,36°04'08″N)位于青岛附近海域,处于底层水温数据指示的黄海冷水团边缘温度锋面处。观测站点水深约27 m左右,附近地形比较平坦。观测设备包含温度链、CTD和ADCP。温度链包含8个温深传感器(TD),8个温深传感器分别布置在水深约3.0,5.5,9.0,12.5,15.5,17.5,20.5和22.5 m处,所有温深传感器的采样率为1 Hz,温度链观测时间从08:14至14:40。海流观测采用1 200 k Hz RDI Workhorse型四波束ADCP,观测时间从10:00至14:20,ADCP采样间隔为10 min,层厚为2 m,第一层深度为2.53 m。CTD采用RBR XR-620,分别在12:00,12:36,13:30,14:24开展全水深CTD剖面观测。
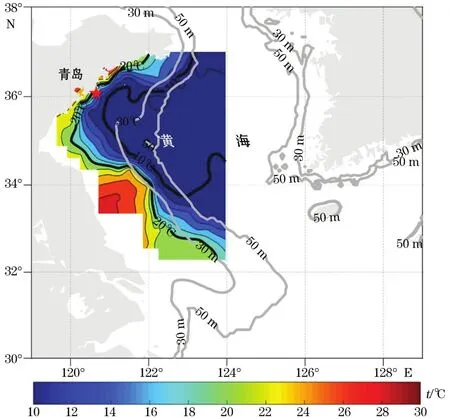
图1 观测海区Fig.1 Map of the observation area
2 观测结果
图2所示为潮流、等温线和ADCP相对后向散射强度观测结果。由图2a可见,12:30之前,正压潮流(ADCP观测流速剖面的深度平均)为西向(向岸)并处于涨潮阶段。由图2b可见,在涨潮阶段,从10:00开始,水体的等温线显著抬升(指示水温下降)。由于观测站点位于黄海冷水团的温度锋面,站点东侧的水温较低,西侧水温则较高(图1),并且此时正处于日照强度增强阶段,因此等温线的显著抬升(水温下降)应由于潮汐推动的温度锋面移动引起的。
观测站点水深相对较浅,盐度随深度变化很小,由等温线所刻画的内孤立波的变化可以划分为4个阶段(图2b),从9:00到9:30为阶段A,上凸式第一模内孤立波占主(称为IW A)。从10:48到10:57为阶段B,第一模内孤立波出现了极性反转,上凸式内孤立波变为了下陷式内孤立波(称为IW B),这一内孤立波极性变化现象和此前在崂山湾观测的结果类似[22]。然后,在10:57到11:12为阶段C,在这一阶段,由向相反方向起伏的等温线可知,此时出现了一个外凸式的第二模内孤立波。从10:27到12:00为阶段D,由于这一阶段对应周期较大的等温线起伏,因此这一段应不是一个单纯的内波过程,我们将这一段的大周期等温线起伏标记为IW D。图2c所示为相对后向散射强度,即将ADCP测得的回声强度数据进行了距离和吸收补偿,所得相对后向散射强度为与距离无关量,但由于没有针对ADCP具体声源特性进行修正(常数),因此所得结果为去掉一个常数的相对值。由ADCP的回声强度导出的相对后向散射强度数据同样清晰地刻画出了IW C和IW D的形状。由于ADCP的时域采样间隔仅有10 min,IW B的形状没有被ADCP的后向散射强度数据明显地体现出来。
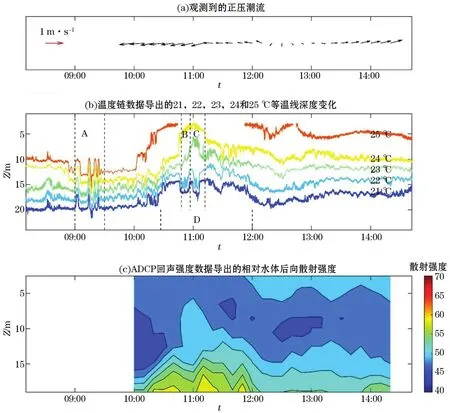
图2 潮流、等温线和ADCP相对后向散射强度观测结果Fig.2 Observed tide,isotherms,and relative backscatter strength of water column
3 理论模型
Kd V(Korteweg-de Vries)方程被经常用来描述内波的特征[25]:
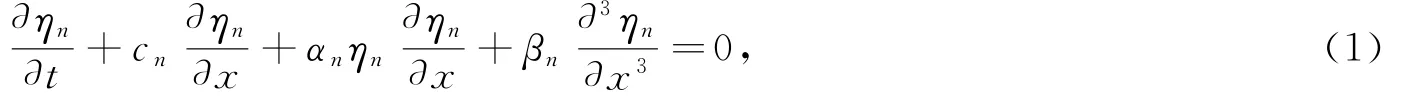
式中,角标n表示内孤立波的模态号数,ηn为层结界面的垂直起伏,c n为线性相速度,αn为非线性系数,βn为频散系数。ηn的解析解为平方双曲正割函数:
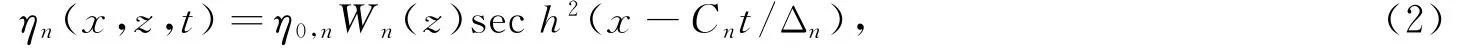
式中,η0,n为幅度,C n为非线性相速度,Δn为非线性特征宽度。图3a至3c为IW C和IW D用式(2)拟合的结果。可见,实测曲线和拟合结果非常接近。IW C基本位于IW D的顶部。
等密面起伏的垂直分布函数W n(z)由Taylor-Goldstein方程控制,在刚盖假设条件下,表示为

式中,N(z)为浮力频率。图3e为利用图3f所示的温度剖面计算得到的浮力频率剖面(由全水深CTD数据可知,盐度剖面垂直变化很小,温度链之上和之下的水温分别和顶部和底部的TD温度接近,因此,此浮力频率剖面由温度链在10:45观测到的温度剖面数据和CTD在12:00观测到的盐度剖面数据计算得到)。利用此浮力频率剖面进一步计算得到了等密面起伏的垂直分布函数(如图3f灰色曲线所示)。

图3 内波的水平和垂直结构Fig.3 Horizontal and vertical structure of the observed internal waves
利用温度守恒方程,并假设非线性作用以及水平平流可以忽略,垂直流速w通过温度链的温度数据导出[4,25]:

式中,Th(z,t)为30 min高通滤波后的温度,Tb(z,t)为30 min低通滤波后的温度。从11:03到11:07的温度链数据(即第二模内孤立波IW C的后半部分)被用来计算w。图3f所示即为第二模内孤立波理论的垂直结构W2(z)和计算得到的w(z)的比较。可见理论和实测的第二模内孤立波的垂直结构相当一致。
内波的非线性系数αn和频散系数βn与水深和层结有关,是描述内波特征性质具有代表性的参数[4],
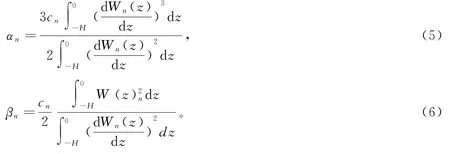
第一模态内孤立波在当α1发生变号时发生极性反转,即当α1为负时对应下陷波,为正时对应上凸波。计算得到的α1在10:30之前为正,对应上凸内孤立波IW A,然后α1变号成为负值,对应产生了下陷式内孤立波IW B。理论计算的α1的符号变化和实际观测的内波极性变化相一致。
Ursell数U n是αn和βn的比值,是内波波形的一个描述手段:

对于一个越小的Ursell数,波形越趋于正弦函数曲线。而当Ursell数越大时,波形越趋向于孤立波[4]。根据观测数据的计算结果显示,第二模内孤立波的非线性系数α2从10:24开始快速上升,而β2则显著下降,相应造成Ursell数也显著上升,对应此时第二模内孤立波(IW C)的形成。
在这些过程中,由于观测站点的水深和背景流几乎不变,因此起主要的作用的变量即为层结的变化。由第二部分的分析可知,层结的变化应主要由于潮汐推动锋面移动引起的,因此,我们推断这里观测到的内孤立波从第一模到第二模的变化主要是由潮汐推动锋面引起的层结变化导致的。
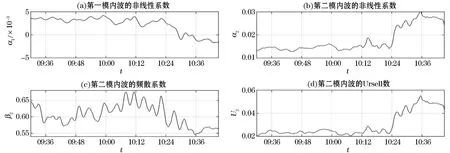
图4 计算得到的Kd V方程系数Fig.4 Calculated coefficients of Kd V equation
4 结 语
我们介绍了在青岛附近海域观测到的局地内孤立波模态从第一模态迅速变化为第二模态的过程。所观测到的第二模内孤立波的波面起伏和垂直结构和理论结果吻合良好。涨潮引起层结变化导致的内波环境函数(U n,αn,βn)变化能够良好对应于观测到的第二模内孤立波的产生。因此,我们推断所观测到的内孤立波模态从第一模向第二模的转化的原因可能为:由于涨潮推动温度锋面移动,引起层结快速变化并进而导致第二模内孤立波的生成。
层结对第二模内孤立波的生成至关重要。在深海,较深的层结较有利于这种内孤立波的生成。比如在南海,由于跃层从夏季到冬季不断加深,观测到第二模内孤立波的发生频率也不断增加[4]。在青岛附近海域的浅海地区,涨潮引起了温跃层的抬升,反而更有利于第二模内孤立波的生成。而且在2 h内发生的层结变化就足以引起内波模态的变化。之前有关内孤立波模态变化的研究主要集中在内波在向岸传播过程中,随着地形变化引起的层结变化对内孤立波模态的影响。本文介绍的观测结果则重点体现了局地层结的快速变化对第二模内孤立波生成的影响。
在黄海海域,潮流和内波引起的湍流混合非常强[7]。由于第二模内孤立波引起的湍流混合和第一模内孤立波接近,这里观测到的潮致第二模内孤立波可能在青岛附近海域的湍流混合具有重要作用。今后可通过开展更加细致的现场观测来深入了解这一过程,相关结果将可能提高区域海洋模式模拟水平。
