层理和裂隙对镐型截齿破煤的影响

李 立

(山西汾西矿业(集团)有限责任公司 双柳煤矿，山西 柳林 033300)

煤岩特性对煤岩开采具有显著的影响，因此深入研究煤岩中广泛存在的层理和裂隙、使采煤机故障率增加的包裹体和小断层等特性，建立与采煤机破煤过程相符的含煤岩特性的煤岩三维模型，使用动力学仿真软件模拟镐型截齿破煤过程，分析镐型截齿在截割含不同特性的煤岩时截割力的变化[1-4]。在煤岩开采机械化和煤岩开采向着大规模、高效率发展的当下，本课题的研究对预测和控制采煤作业中镐型截齿截割力的波动范围、降低采煤机故障率、提高采煤机工作的可靠性、增加煤矿企业的经济效益都具有十分重要的实际应用价值[5-8]。

现有的镐型截齿破煤过程的研究工作主要集中在镐型截齿结构的优化、安装参数的改变等方面，同时，大多数的研究是在直线截割的情况下和均质煤岩的基础上进行计算模拟，对镐型截齿进行动力性能分析，未考虑煤岩特性对镐型截齿破煤的影响，尤其还未考虑镐型截齿与煤岩间发生非连续冲击下的力学突变行为，因此探讨煤岩特性对镐型截齿截割载荷的影响，对完善本学科具有重要的理论意义[9-11]。

1 基于分形理论煤岩裂隙的研究

煤岩中裂隙的长度和密度等参数具有很大的随机性和偶然性。国内外许多学者在某种特定尺度使用抽样统计和试验分析等方法，对煤岩裂隙的密度和尺度进行测量和预测，但是这两种方法不能向更大或更小的尺度推广[12，13]。为此，本文运用分形理论对煤岩中的裂隙进行描述和研究。

1.1 煤岩中裂隙的分形统计

采集某煤矿同一煤层煤块若干，使用钻孔取芯机对煤块进行钻取，取出五块直径为50mm的煤样，然后使用锯石机分别将五块煤样锯成高度为25mm的圆柱体，最后用磨平机将煤样两端磨平。选定煤岩试件其中一个底面为观察面，使用白色粉笔分别将五块煤样的观察面涂满，之后把观察面上的粉笔痕迹擦除，白色粉笔末会存留于煤样观察面的裂隙之中，可以更为清晰的对煤岩裂隙进行观察。对处理后的五块煤样进行编号，其编号顺序为1至5号，如图1所示。

图1 煤岩试件

由于煤样的观察面为圆形，无法有规律地划分出若干个大小相等且面积也相等的图形，因此在五个观察面上分别选出35mm×35mm的正方形。由于硫酸纸具有良好的透明性，所以使用硫酸纸对煤样观察面的裂隙进行描摹。在硫酸纸上打印出边长为35mm×35mm的大正方形五个，且大正方形被64个小正方形均分，将硫酸纸上正方形置于煤样观察面上选定的正方形内，把观察面上正方形区域内的裂隙迹线描摹于硫酸纸上，印有裂隙迹线的硫酸纸如图2所示。

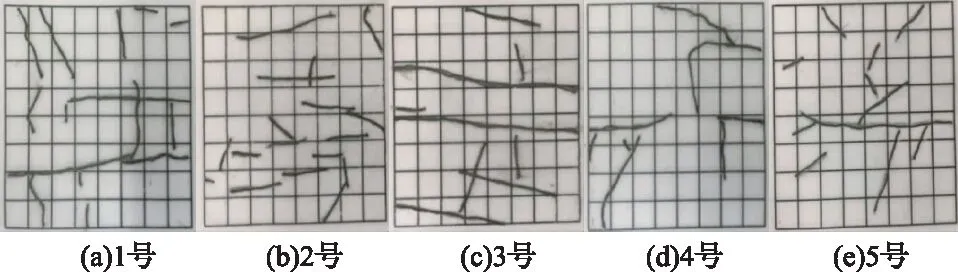
图2 煤岩试件裂隙迹线描摹图

裂隙不规则地、复杂地分布在煤岩中，在测量裂隙时难以分辨不同种类的裂隙，为方便测取数据，采用裂隙穿过网格尺度-视条数的分形测量方法测量煤岩中裂隙的长度和条数[3]。

对1至5号煤样的分形视条数进行统计，为使裂隙的分析结果更具有客观性，汇总数据求出相同网格尺度下裂隙视条数的平均值，见表1。

表1 煤样1至煤样5分形统计数据

1.2 分形直线的建立

以lnL为横轴，lnn(L)为纵轴，通过若干个点拟合出来的一条斜线，称为网格尺度-裂隙视条数的分形直线。对表1中的数据进行处理计算后可以得出拟合分形直线的A，B，C，D四个点[4，5]，见表2。

表2 分形直线拟合点

通过表2中的数据可以得到如图3所示的关于网格尺度和裂隙视条数的一条分形直线，图3中直线的斜率为裂隙迹线穿过尺度-视条数的分形维数d[6-8]。

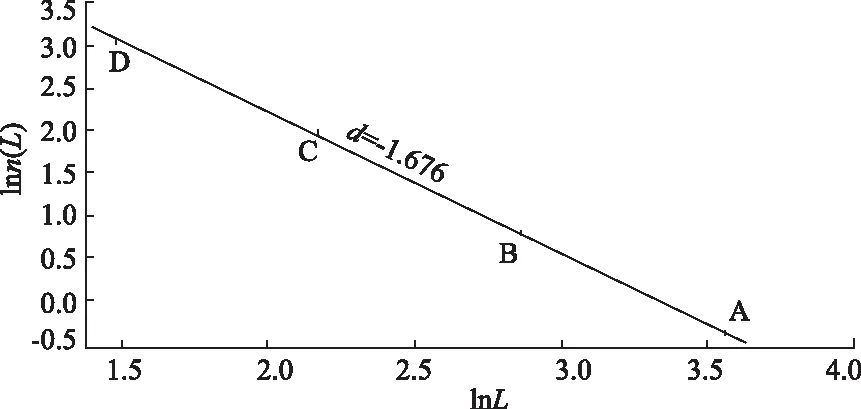
图3 网格尺度-裂隙视条数分形直线

分形直线的函数关系式为：

lnn(L)=-1.676lnL+5.581

(1)

1.3 煤岩中裂隙的长度与数量的关系

对式(1)进行简化，得出网格尺度L和裂隙视条数n(L)的函数关系：

n(L)=e5.581L1.676

(2)

根据式(2)可以得出裂隙视条数随网格尺度变化的关系曲线，如图4所示。

图4 网格尺度-裂隙视条数关系曲线

从网格尺度-裂隙视条数的关系曲线可以看出，网格尺度在1～3mm之间时，裂隙视条数迅速减小，但处于此区间的裂隙较多；随着网格尺度的增加，裂隙视条数以较小的幅度下降。网格尺度不小于5mm时，所统计的裂隙视条数见表3。

表3 裂隙视条数统计值

裂隙迹线通常为不规则的线条，因此裂隙的实际长度会略大于网格边长，为了方便后续建模，把裂隙看作为长度等于网格边长的直线。计算裂隙视条数时，会对同一条裂隙多次计数，因此，要确定煤岩内实际的裂隙数量，应仅保留最大穿过网格尺度时裂隙的数量。在35mm×35mm的方格内，裂隙的长度和数量统计见表4。

表4 裂隙的长度和数量统计

2 含层理和裂隙煤岩模型的建立

2.1 煤岩模型中层理和裂隙的假设

为了实现层理和裂隙对镐型截齿破煤影响的研究，考虑到层理和裂隙在煤岩中分布的特点，对煤岩三维模型中层理和裂隙的建立提出以下几点假设[9，10]：①煤岩中的次内生裂隙、第三级裂隙、第四级裂隙和接缝一般分布在两层理之间，具有较差的贯穿性且交叉分布在煤岩中，对镐型截齿破煤的影响较少，因此本文仅考虑主内生裂隙对镐型截齿破煤的影响；②上节中对煤岩裂隙的长度和条数之间的关系进行了分析，计算得出裂隙的最大长度为28mm，本文假设煤岩三维模型中所有裂隙长度均为28mm，且均匀分布在煤岩模型中；③设定煤岩模型中裂隙的宽度为0.5mm；④煤岩中层理为两个煤层间的弱结合面，但为使动态仿真过程中可以实现对层理的研究，假设层理为0.5mm宽度的裂隙。

2.2 模拟方案设计

1)对镐型截齿截割均质煤岩(不含特性的煤岩)进行模拟，通过对比说明煤岩层理和裂隙对煤岩截割的影响。

2)煤岩分布的多样性，致使不同工况下，镐型截齿截割煤岩中的层理与水平面呈不同角度，因此本文分别模拟层理与水平面的夹角α呈0°、30°、60°、90°时，层理和裂隙对镐型截齿破煤的影响。在Pro/E三维建模软件中对镐型截齿破煤三维模型进行层理和裂隙的划分。

3)在不影响仿真模拟的前提下，为减少前处理时划分网格的数量，以缩短计算时间，设定均质煤岩模型和含层理、裂隙煤岩三维模型的长度a均为1.2m。

3 模拟前处理

3.1 单元类型、材料模型与网格划分

煤岩和镐型截齿均为固体，因此采用只适用于显示动力分析中的三维实体solid164单元，solid164单元由8个节点组成，每个节点均具有9个自由度，即位移自由度UX、UY、UZ，速度自由度VX、VY、VZ，加速度自由度AX、AY、AZ。虽然全积分单元算法(Full Int)可以避免计算过程中产生的沙漏问题，但ANSYS/LS-DYNA的分析计算时间相对于单点积分算法(Const.Stress)会成倍数地增加，因此综合考虑本文动态仿真模拟采用单点积分算法[11-13]。

LS-DYNA材料库中含有100多种材料模型，能够满足绝大多数模拟仿真的需要。前文对煤岩性质进行了分析，选用*MAT_DRUCKER_PRAGER作为煤岩的材料模型，由于在ANSYS中进行前处理操作时，ANSYS中材料库中没有此模型，因此可以在前处理时任意设定煤岩的材料模型和材料参数，最终在生成的K文件中对煤岩的材料模型和材料参数进行修改。由于镐型截齿的强度远大于煤岩的强度，因此设定刚体模型(RIGID)为镐型截齿的材料模型，以加快求解计算时间。将镐型截齿的材料参数设定为：密度7800kg/m3，弹性模量270GPa，泊松比为0.3，同时设置镐型截齿的约束情况，镐型截齿破煤过程中有两个方向的自由度，X方向的位移自由度和绕Z轴方向的旋转自由度，对其他方向的自由度进行约束。

3.2 定义接触、约束及加载

模拟镐型截齿破煤过程中，镐型截齿的表面会穿过煤岩表面，因此定义煤岩和镐型截齿之间的接触为面面接触。定义镐型截齿和煤岩的接触之前，需定义接触面和目标面，设定接触面为镐型截齿Part1单元，目标面为煤岩Part2单元。由于镐型截齿破煤过程中，煤岩由于受到镐型截齿的截割作用而破碎，因此采用面面接触中的侵蚀接触算法，该算法在两个Part单元间接触过程中可以致使某个Part单元接触部分发生材料失效，但两个Part单元间的接触仍然会在剩余单元中继续。

在前处理操作中要合理地定义每个Part单元的约束条件，以保证可以实现仿真模拟。镐型截齿Part1单元的约束条件在3.1中定义镐型截齿材料时已完成设置，本小结不再赘述。对于煤岩Part2单元，首先在煤岩模型的表面施加无反射边界条件，模拟分布在地下的、无限大的煤层；其次，对煤岩模型的底部、背部和顶部添加全约束。

4 模拟结果分析

4.1 镐型截齿截割均质煤岩时的截割力分析

镐型截齿截割均质煤岩时截割力变化如图5中(a)所示，对应图5(a)中A、B、C、D四个时刻的镐型截齿破煤状态如图5(b)(c)(d)(e)所示。由图5(a)可知，截割力在镐型截齿破煤过程中呈现出不规则的波动，这是由于煤岩各向异性的性质和崩落煤块的大小不同；在镐型截齿破煤过程中所受到的截割力呈现出一组组峰值曲线，这是由于在密实核崩落之前，镐型截齿受到的截割阻力逐渐增大直到形成峰值，在密实核崩落的短暂的时间内，镐型截齿迅速减小至零，截割力从零到达峰值再减小至零，镐型截齿完成一次截割，仿真模拟结果与镐型截齿破煤原理相吻合；从整体上看，镐型截齿截割均质煤岩时所受到的截割力呈先增大后减小的变化趋势，这种现象产生的主要原因是镐型截齿破煤过程中截割厚度的变化导致的，镐型截齿刚刚进入破煤过程时镐型截齿截割煤岩的深度较浅，较小的截割力就可以将煤岩截割下来，在截割力变化曲线中表现为截割力峰值较小，随着截割厚度的增加，截割力的峰值也开始增加，在3500μs时刻左右，截割厚度达到最大值，但截割力最大值并未在此阶段产生，而是在4500μs时刻左右产生，这是由于此时镐型截齿破煤以挤压破坏为主、剪切破坏为辅对煤岩进行截割，而煤岩的抗压强度远大于抗剪强度。

由图5(a)可以看出，镐型截齿破煤过程中，会发生镐型截齿所受到的截割力为零或趋近于零的情况，这是由于煤岩硬脆性的性质导致的，当镐型截齿截割到A点，如图5(b)所示，镐型截齿开始截割煤岩，由于镐型截齿的剪切和挤压作用导致大块煤岩被剥落，被截割后的煤岩如图5(c)所示，由于煤岩崩落的块度较大，导致镐型截齿出现短暂的空载期，图5(d)为镐型截齿处于空载期的状态图，在空载期镐型截齿所受到的截割力为零，直到截割到D点开始镐型截齿开始下一次截割，截割状态如图5(e)所示。

4.2 镐型截齿截割 含层理、裂隙煤岩时的截割力分析

层理与水平面呈0°、30°、60°、90°夹角时镐型截齿所受到的截割力变化分别如图6(a)(b)(c)(d)所示。由图6可知，四种工况下截割力在总体上均呈现先增大后减小的变化规律，这是由于镐型截齿截割厚度的变化导致的。

虽然四种工况下，截割力变化的大体趋势相同，但由于煤岩模型中层理、裂隙分布的不同，每种工况截割力的变化情况有一定的差异。当层理与水平面呈0°和90°夹角时，截割力随截割厚度的变化而变化，且截割力的增加或减小较为稳定；当层理与水平面夹角呈30°和60°夹角时截割力变化较为复杂，在1000～7000μs之间镐型截齿截割力大多数的峰值在一定的范围内，截割力变化趋势与截割厚度变化的关系不明显，这是由于当镐型截齿截割层理与水平面呈30°和60°夹角时由层理和裂隙将煤岩划分成一个个菱形截面，越靠近煤岩顶底板，菱形截割面的面积越大，煤岩是沿着层理和裂隙破坏的，即使镐型截齿的截割厚度较小，但被剥落的煤岩的截割面面积较大，镐型截齿需要较大的截割力截割下煤岩，因此截割力呈现出较为复杂的变化情况。

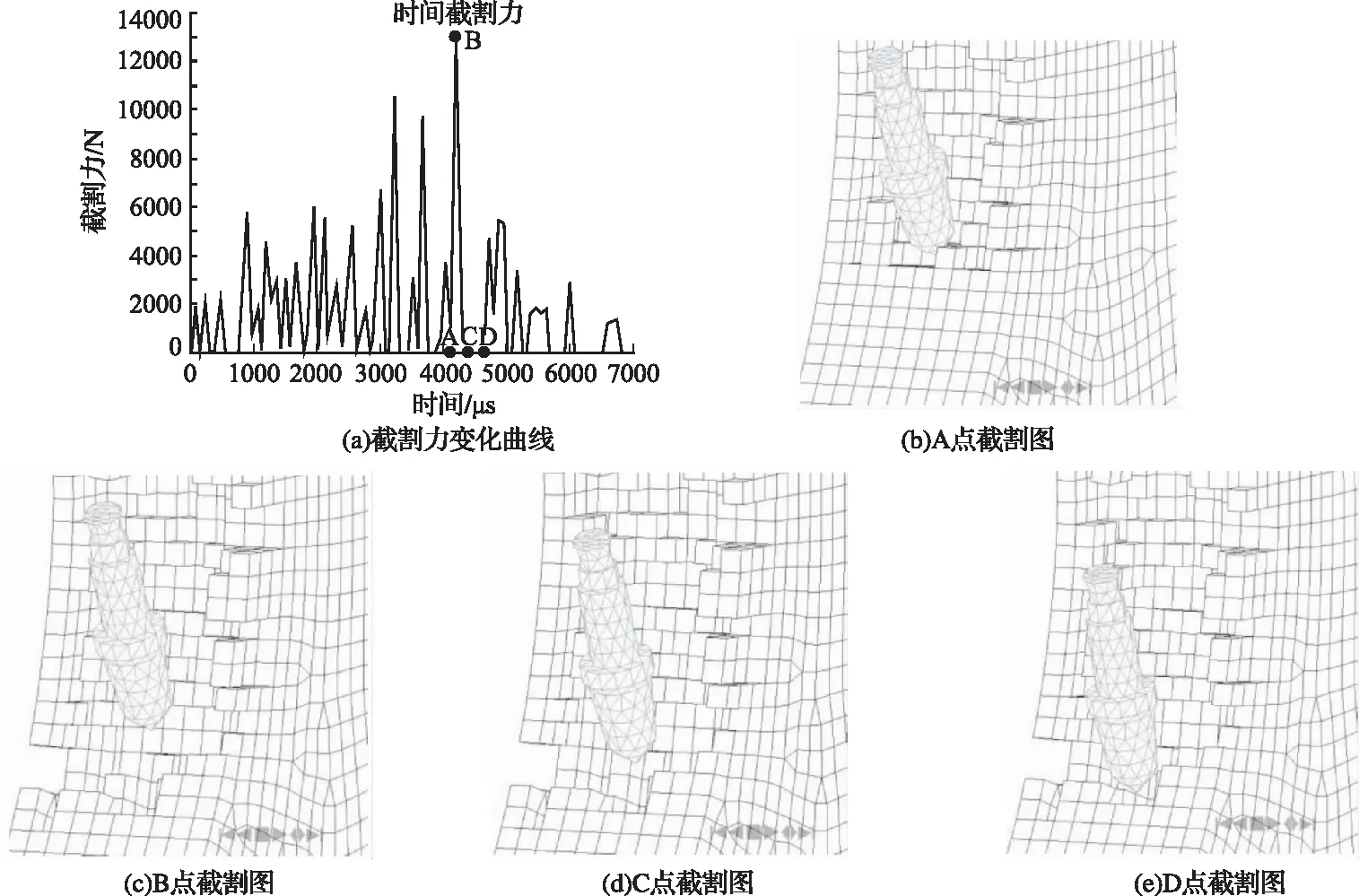
图5 镐型截齿截割均质煤岩过程及截割力变化曲线

图6 含层理、裂隙煤岩截割力变化曲线

由图6可以发现镐型截齿截割含层理、裂隙煤岩时，截割力的最大峰值不一定发生在截割厚度最大时，且最大峰值远大于其他峰值的情况，这是由于镐型截齿截割块煤体积越大，镐型截齿所受到的截割力越大，煤岩的脆性、非线性和煤岩沿着层理、裂隙剥落等原因，导致最大截割力不一定在最大截割厚度处发生。

对比镐型截齿截割均质煤岩时截割力曲线变化情况与截割含层理、裂隙煤岩时截割力曲线变化情况发现，后者镐型截齿出现空载次数明显少于前者，这是由于当镐型截齿截割均质煤岩时，煤岩出现随机性的大块崩落，如果崩落煤岩体积过大，就会出现截割力为零的情况；当镐型截齿截割含层理、节理煤岩时，煤岩沿着层理和裂隙崩落，崩落煤岩的体积不会过大，因此镐型截齿截割含层理、裂隙煤岩时，镐型截齿很少出现空载现象或空载现象持续时间较短。

上述通过对不同工况下镐型截齿受力曲线图来分析煤岩特性对镐型截齿受力的影响。将截割力数据从LS-PREPOST后处理器中导出，并在excel中进行处理后所整理出的不同工况下镐型截齿所受到截割力的平均值、最大值和均方差三个参数(见表5)，以进一步分析层理和裂隙对镐型截齿破煤的影响。

表5 不同参数下截割力统计值 N

从表5可以看出，镐型截齿截割均质煤岩时，所受到截割力的平均值、最大值和均方差均大于镐型截齿截割含层理、裂隙煤岩时所受到的截割力，与煤岩层理和裂隙有助于镐型截齿破煤的实际情况相符。均方差反映镐型截齿所受到截割力的波动性，截割力波动性越大，镐型截齿越容易失效，因此均方差越小越好，当层理与水平面夹角为0°时，镐型截齿受到的均方差最小且平均值最小，随之层理与水平面夹角的增加，三组参数均有所增加。

5 结 论

1)文中首先应用分形理论对煤岩体中的裂隙长度与数量的关系进行了分析，建立了三维模型，对某矿取出五块直径为50mm的煤样，通过煤岩中裂隙的分析统计，得出网格尺度L和裂隙视条数n(L)的函数关系：n(L)=e5.581L-1.676。

2)为了实现层理和裂隙对镐型截齿破煤影响的研究，考虑到层理和裂隙在煤岩中分布的特点，建立了含层理和裂隙煤岩模型，本文分别模拟层理与水平面的夹角α呈0°、30°、60°、90°时，层理和裂隙对镐型截齿破煤的影响。在Pro/E三维建模软件中对镐型截齿破煤三维模型进行层理和裂隙的划分。

3)模拟结果表明镐型截齿截割均质煤岩时，所受到截割力的平均值、最大值和均方差均大于镐型截齿截割含层理、裂隙煤岩时所受到的截割力，与煤岩层理和裂隙有助于镐型截齿破煤的实际情况相符。均方差反映镐型截齿所受到截割力的波动性，截割力波动性越大，镐型截齿越容易失效，因此均方差越小越好，当层理与水平面夹角为0°时，镐型截齿受到的均方差最小且平均值最小，随之层理与水平面夹角的增加，三组参数均有所增加。