基于等效弹簧斜撑的填充墙RCS组合框架结构抗震性能研究

倪伟杰, 潘志宏

(江苏科技大学 土木工程与建筑学院, 镇江 212003)

钢筋混凝土柱-钢梁组合框架结构(rein-forced concrete column and steel beams composite frame structure,RCS)是一种新型结构形式,即由钢筋混凝土柱和钢梁组合成的框架结构,它充分发挥了钢与混凝土材料的优点,钢材具有较好的抗拉强度与延性,混凝土具有优良的抗压强度和较大的刚度,并且混凝土提高了钢材的屈曲能力．目前国内外学者对于RCS组合结构的研究大部分集中于框架梁柱节点[1-2],然而对于框架整体以及考虑填充墙效应的抗震性能研究较少．历次震害研究表明[3],填充墙与框架是协同工作的,填充墙为框架提供了较大的侧向刚度,在地震中承担了部分剪力,耗散了地震的能量[4-5]．但是它自身的重量和承担的剪力也增加了整体结构吸收的能量,这对于结构来说是有害的．在2008年汶川8.0级地震中,砌体结构的破坏程度尤为严重,其中包括不少学校教学楼和医院等公共建筑,值得注意的是,由于墙板的约束作用,地震中很多框架结构发生“强梁弱柱”的破坏模式,与抗震设计预期不符;另外大量填充墙出现不同程度和形式的破坏甚至倒塌,严重影响了人员的生存空间和灾后救援工作,惨痛的教训提醒我们必须加强对框架中填充墙的影响作用的认识和研究．

2002年,我国台湾与美国、日本合作对一个3层3跨的实尺寸RCS组合框架进行了拟动力试验研究[6],现场图片如图1．此试验基于两个强震记录,依次选取代表多遇烈度(1个)、基本烈度(2个)、罕遇烈度(1个)的4个地震波进行推倒试验．推倒过程中,二层钢梁首先屈服,一、三层钢梁下翼缘局部屈曲,边梁局部屈曲较大,一层柱底轻微开裂,接着,钢梁从二层到一、三层大量屈服,下翼缘和腹板有较大屈曲,一层柱底混凝土开裂,保护层脱落,整体结构主要以梁铰屈服破坏为主,基本实现了现行规范要求的“强柱弱梁”[7-8]失效机制．现实生活中人们为了满足建筑物功能的需要,往往会出现一些对填充墙不合理布置的情况,导致了薄弱层的出现,例如,很多住宅、办公楼会在底层设置商店、停车场等,形成底部薄弱层;住宅装修过程中,中间层的住户有时会取消部分填充墙,在结构中部形成中部薄弱层;建筑物的上层有时会布置会议室和运动场所,上层的填充墙布置将减少,形成顶部薄弱层．这种因填充墙沿竖向布置不均匀而产生的薄弱层会对框架结构的抗震性能产生不利的影响．为了研究填充墙的布置方式对于RCS组合框架结构抗震性能的影响,文中将以文献[6]中的3层3跨的实尺寸RCS组合框架拟动力试验为基础建立一个3层4 跨×3 跨RCS组合框架结构计算模型,试验模型基于一个6跨×4跨的虚拟三维框架结构,如图2．利用SAP2000中的LINK单元建立填充墙等效弹簧斜撑模型,对不同填充墙布置方式的模型进行模态分析和pushover分析．

图1 现场图片Fig.1 Live picture

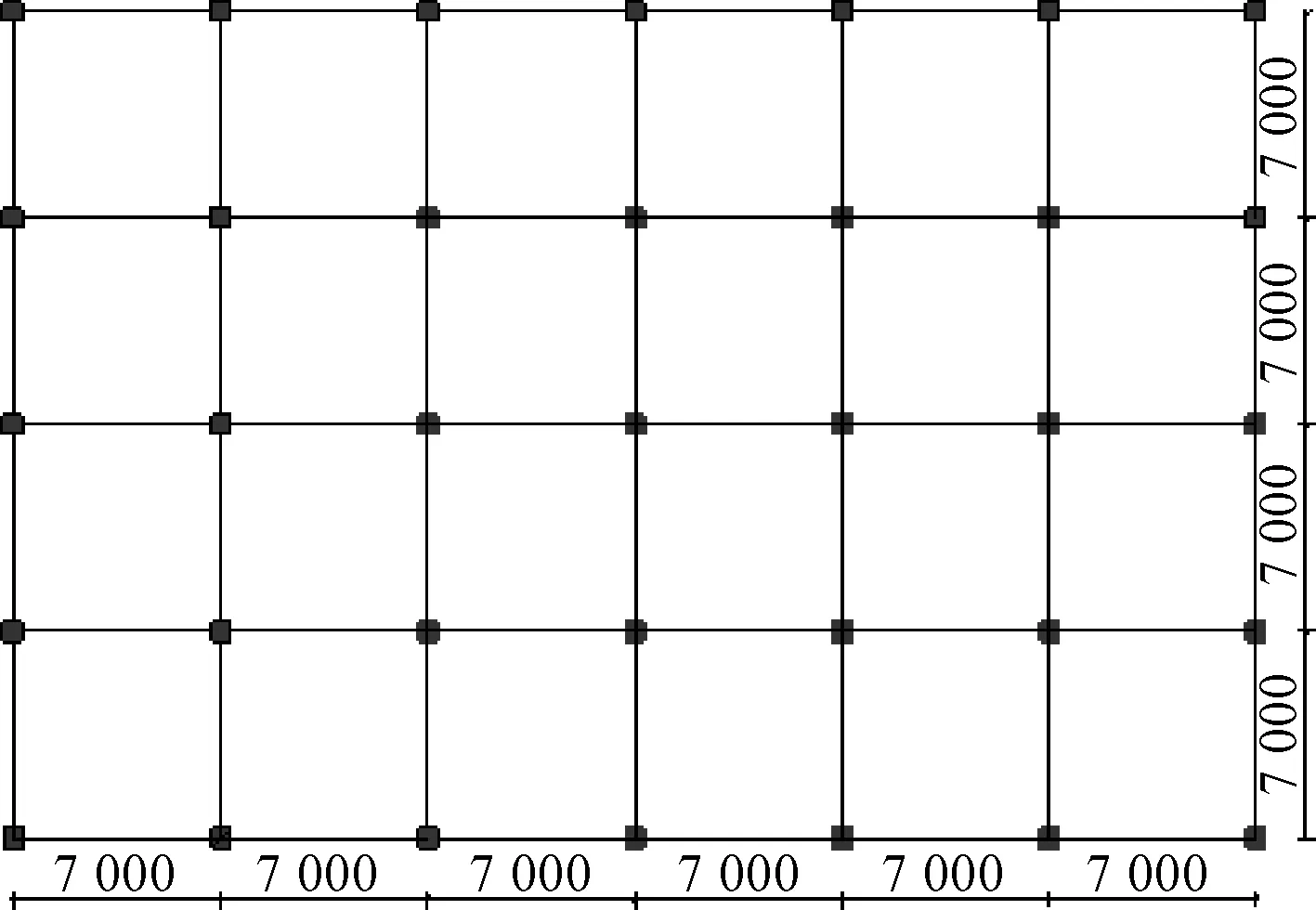
图2 虚拟三维框架结构平面图(单位：mm)Fig.2 Layout of the virtual three-dimensional framework(unit:mm)

1 填充墙等效弹簧斜撑模型

在关于框架的填充墙研究中,主要有墙-框并联模型、等效斜撑模型、填充墙元模型等,文中计算分析中填充墙的力学模型采用文献[9]推导出的填充墙等效弹簧斜撑模型,该模型的主要等效原则是:填充墙和非线性弹簧质量相等,抗侧刚度等效,填充墙质量以荷载形式施加在框架梁上．最终推导得到的等效弹簧的轴向刚度为:

式中:h、t、b分别为填充墙的高度、厚度和宽度;θ为等效弹簧斜撑与水平方向的夹角;Ew为砌体的弹性模量；Kw为填充墙的抗侧刚度；β为考虑到填充墙上有洞口时引入的洞口刚度影响系数,因为文中所研究的模型不需要考虑洞口的影响,即开洞率为零,根据文献[10],β一律取1代入计算．

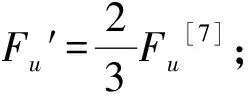
图3 填充墙的恢复力模型Fig.3 Restoring force model of infilled wall

2 工程概况

为了研究填充墙对RCS框架结构抗震性能的具体影响,以文献[6]中的3层3跨实尺寸RCS组合框架拟动力试验为基础建立了一个3层教学楼框架结构计算模型,整体的结构平面布置如图4,框架的梁柱尺寸取自文献[6]．

图4 结构平面图(单位：mm)Fig.4 Structure layout(unit:mm)

各层层高4 m,钢梁采用Q235钢材,每层钢梁横梁和次梁截面一样,1～3层分别取H600 mm×200 mm×11 mm×17 mm、H500 mm×200 mm×10 mm×16 mm、H396 mm×199 mm×7 mm×11 mm,1～3层框架柱分别为Z1、Z2、Z3,柱截面配筋如图5,板厚120 mm,板、柱混凝土强度等级C45,弹性模量为3.35×104MPa,填充墙厚240 mm,砖强度等级为MU10,M5砂浆,砌体弹性模量为2.4×103MPa,质量密度为19 kN/m3．受力筋和箍筋均选用HRB500钢筋,楼面活载为2 kN/m2,教学楼走廊活载为2.5 kN/m2．设防烈度为8度,Ⅱ类场地,设计地震分组为第二组．

3 有限元模型的建立与分析

3.1 有限元建模

实际工程中,设计人员会根据建筑使用功能来布置填充墙,为此采用SAP2000软件建立了5个模型以考虑不同填充墙布置对RCS结构的影响．其中模型一为纯框架结构,模型中仅考虑填充墙的质量,如图6(a);模型二为满布填充墙框架结构,如图6(b);模型三为考虑底层作为商业用途不布置填充墙,上面两层满布填充墙的框架结构,如图6(c);模型四为考虑中间层作为商业用途不布置填充墙,底层和顶层满布填充墙的框架结构,如图6(d);模型五为考虑顶层作为商业用途不布置填充墙,中间层和底层满布填充墙的框架结构,如图6(e)．

采用SAP2000中提供的LINK单元,建立填充墙等效斜撑模型,填充墙厚度t取240 mm,弹性模量为2.4×103MPa,根据力-变形关系定义LINK单元中U1方向的非线性弹簧,填充墙和非线性弹簧的具体参数如表1．连接类型选择MultiLinear Plastic,墙体的荷载直接施加在框架梁上．用模型二、模型三、模型四、模型五与模型一对比,分析加入填充墙及不同填充墙布置方式对RCS组合结构抗震性能的影响,主要是对塑性铰发展顺序的影响,用模型三、模型四与模型五相互对比,分析填充墙数量一样时,不同的填充墙布置方式对结构自振周期的影响．

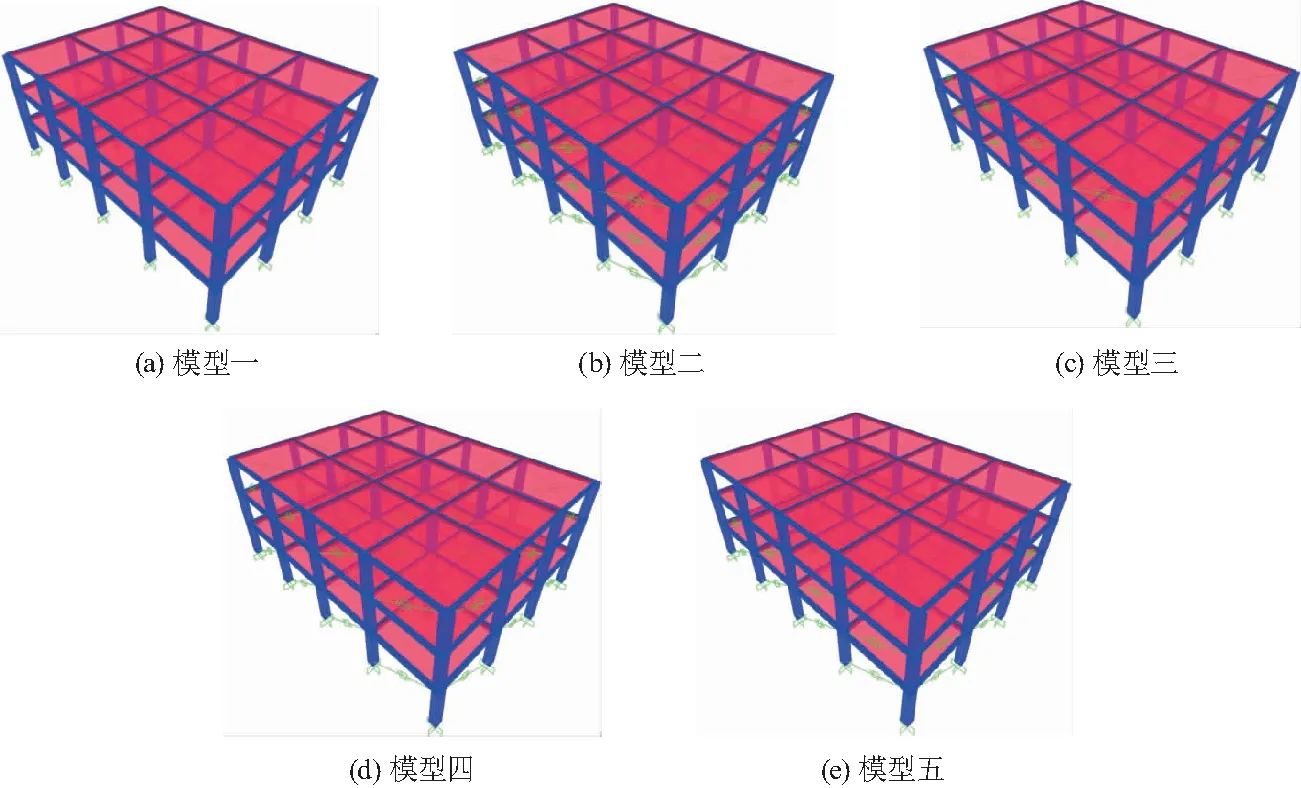
图6 填充墙等效模型Fig.6 Infilled wall equivalent model

表1 模型参数

3.2 模态分析

对5个模型分别进行模态分析,取以x向和y向平动为主的前2阶振型和以扭转为主的第3阶振型进行结果对比分析,得到的自振周期以及不同模型间周期对比如表2 ．由表2可知,模型二、模型三、模型四和模型五较模型一自振周期有了明显降低,周期折减系数在0.3～0.6左右,略小于我国《高层建筑混凝土结构技术规程》JGJ3-2010第4.3.17条第一款规定的框架结构周期折减系数0.6～0.7,这是因为在模型二中满布填充墙,填充率100%,模型三～五填充墙填充率66.7%,所选取得填充墙模型填充率较大,填充墙对框架的刚度贡献较大,模拟所得的自振周期折减系数较一般框架结构小,由此可知,规范规定的框架结构周期折减系数是较合理的．

表2 模型自振周期

3.3 Pushover分析

3.3.1 塑性铰本构模型

SAP2000中塑性铰的本构关系如图7,其中A为原点,B为塑性铰的屈服点,C点达到塑性铰的极限承载力,D点为塑性铰残余强度,E点为塑性铰失效．在BC段还有3个点IO(直接使用),LS(生命安全),CP(防止倒塌)代表塑性铰的3个能力水平．

Pushover分析的五组模型均是从整体结构中取一榀(轴线1-1方向)进行分析．在模型中,对梁两端指定M-3铰,柱两端指定 P-M2-M3 铰, Pushover分析的侧向力加载模式采用倒三角加载模式．推覆分析方法采用ATC-40能力谱方法,文中主要研究结构在8度罕遇地震作用下的反应,考虑P-Δ效应．按照8度罕遇地震计算,根据我国规范与美国规范中的反应谱对比,取修正系数CA=0.36,CV=0.405[12]．

图7 塑性铰本构模型Fig.7 Plastic hinge model

3.3.2 Pushover 曲线以及性能点分析

对5个模型进行 Pushover分析,得到5个模型的抗侧能力曲线,如图8．从图中可以看出,各模型的能力曲线经历了弹性、弹塑性以及塑性阶段直至破坏．由于填充墙的存在,明显增大了整体结构的刚度．在弹性阶段,基底剪力-顶点位移曲线的斜率即表示RCS结构的侧向刚度,由图8可知,满布填充墙的模型二斜率最大,结构侧向刚度最大．

图8 Pushover能力曲线型Fig.8 Pushover capability curve

根据能力谱法求得能力谱线与需求谱线的交点,即性能点．性能点处结构变形的分析反映了当地震作用为8度罕遇地震时的结构状态．在罕遇地震下,各模型性能点如表3,其中V表示基底剪力,D为顶点位移,性能点处层间位移角如表4,层间位移角直观值如图9．由图9和表4可知在罕遇地震下,模型一的3层层间位移角最大,其值为1/607,加入满布填充墙以后,模型二的最大层间位移角由原来的第3层变成第2层,其值为1/4 286,RCS结构的薄弱层由第3层变为第2层．模型三到五层间位移角最大值分别在第1,2,3层,其值分别为1/2 148,1/1 773,1/1 572,由此可知,填充墙的不利布置将导致竖向刚度不连续,侧向刚度产生突变,从而会造成薄弱层的先行破坏．由文献[13],RCS组合结构性能水平为防止倒塌对应的层间位移角限值为1/50．模型一到五的最大层间位移角均小于其限值,说明结构在罕遇地震下可以满足“大震不倒”的抗震设防要求．

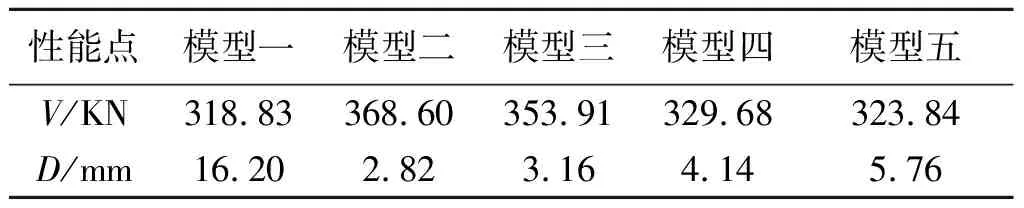
表3 结构的性能点

表4 各模型层间位移角

图9 层间位移角Fig.9 Inter-layer displacement angle

3.3.3 塑性铰的发展过程与分析

图10为RCS纯框架(模型一)塑性铰的发展过程．第2层钢梁首先屈服出现塑性铰(图10(a)); 随着侧向荷载增加,塑性铰向第3层梁和第1层梁蔓延,几乎所有梁端出现塑性铰后,底层柱开始出现塑性铰(图10(b)); 随着侧向荷载继续增加下部2层钢梁和底层柱的塑性铰达到承载能力极限状态,即将退出工作,结构将出现倒塌危险(图10(c))．塑性铰发展情况与文献[4]中的试验结果基本一致,基本实现了规范要求的“强柱弱梁”失效机制,验证了有限元模型的正确性．

图11为满布填充墙RCS框架结构(模型二)塑性铰的发展过程．该模型也是钢梁先屈服出现塑性铰,与模型一相比,钢梁先出现塑性铰的楼层由第2层变为第1层(图11(a));随着侧向荷载增加,底层柱和第2层钢梁开始出现塑性铰(图11(b));继续加载后,第3层钢梁和第2层底柱依次出现塑性铰,最终2、3层钢梁和2层底柱达到承载能力极限状态(图11(c)),与模型一相比,填充墙的加入改变了塑性铰的出铰顺序,加入了填充墙的RCS组合结构在2 层柱底也出现了较为密集的塑性铰,而模型一只出现在了底层柱底位置,分析可能是2层填充墙吸收了较多能量,发生破坏,退出工作,2层柱底因为填充墙的退出而承担较大剪力,故而出现了塑性铰．填充墙提高了结构整体刚度,起到了抗震第一道防线的作用．模型二也实现了规范要求的“强柱弱梁”失效机制．

图10 模型一塑性铰的分布Fig.10 Distribution of a plastic hinge of model one

图11 模型二塑性铰的分布Fig.11 Distribution of a plastic hinge of model two

图12为底层未布置填充墙的RCS框架结构(模型三)塑性铰的发展过程．塑性铰首先底层柱底,而布置填充墙的构件未出现塑性铰(图12(a));随着侧向荷载的增加,第1、2层梁端出现塑性铰(图12(b));继续加载,塑性铰向上层发展,底层柱底达到极限承载力, 即将失效破坏(图 12(c))．由于底层未布置填充墙,导致结构刚度在竖向不连续,底层较柔,使得结构变形主要由底层来承担,加剧底层成为整个结构最先破坏的地方．从该模型的塑性铰发展来看,不符合规范要求的“强柱弱梁”设计准则．

图12 模型三塑性铰的分布Fig.12 Distribution of a plastic hinge of model three

图13为中间层未布置填充墙的RCS框架结构(模型四)塑性铰的发展过程．塑性铰首先发生第1层梁端(图13(a));随着侧向荷载的增加,第2层梁出现塑性铰、底层柱底、第3层梁端依次出现塑性铰(图13(b)); 继续加载,2层柱底开始出现塑性铰,最终2、3层钢梁,2层柱底达到极限承载力,即将失效破坏(图 13(c))．模型四实现了规范要求的“强柱弱梁”失效机制．

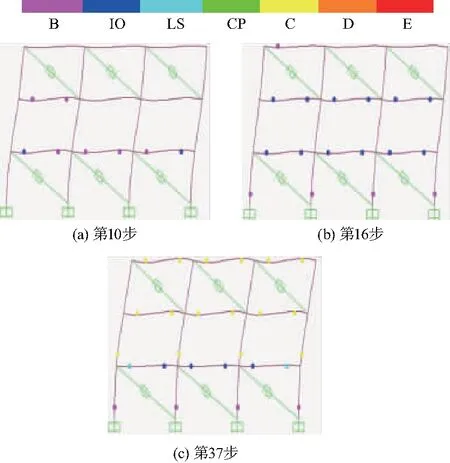
图13 模型四塑性铰的分布Fig.13 Distribution of a plastic hinge of model four

图14为顶层未布置填充墙的RCS框架结构(模型五)塑性铰的发展过程．塑性铰首先发生第2、3层梁端(图14(a));随着侧向荷载的增加,第1层梁出现塑性铰 (图14(b)); 继续加载,2层柱底和底层中间柱底开始出现塑性铰,最终2、3层钢梁,2层柱底达到极限承载力,即将失效破坏(图 14(c))．模型五实现了规范要求的“强柱弱梁”失效机制．对比模型四和模型五,虽然由于填充墙布置位置的不一样导致结构刚度在竖向分布存在较大的差异,但是它们最终达到极限承载力,失效破坏的结果比较相似,且此时底层柱底塑性铰都处于IO(直接使用)的能力水平,而模型一达到极限承载力时,底层柱底塑性铰处在C(强度极限)的能力水平,模型四、模型五这种失效模式相比较文中选取的RCS纯框架结构(模型一)更加合理,在需要按照建筑使用功能布置填充墙时可以考虑这两种布置方式．

图14 模型五塑性铰的分布Fig.14 Distribution of a plastic hinge of model five

4 结论

(1) 文中模拟的RCS纯框架结构塑性铰发展情况与试验结果基本一致,最终形成了“强柱弱梁”的失效机制,并以此为基础对结构施加不同布置方式的填充墙,分析填充墙对RCS组合结构抗震性能的影响,验证了所选模型以及模拟过程的真实性．

(2) 通过分析确定了RCS组合框架结构的填充墙周期折减系数在0.3～0.6左右,略低于规范规定的框架结构折减系数0.6～0.7,这是由于所选模型填充墙填充率高于一般框架结构,填充墙刚度贡献更大,基本验证了规范所给折减系数的合理性．

(3) 罕遇地震作用下,当RCS结构考虑填充墙时,底部薄弱层的出现使得“强柱弱梁”失效机制无法实现;中部薄弱层和顶部薄弱层不影响“强柱弱梁”失效机制实现,结构仍然具有较好的抗倒塌性能．在对RCS组合结构进行结构设计时,可以在楼层中部和顶部适当开设大空间以满足建筑物功能的需要,RCS结构空间利用度高,整体抗震性能优良．