权重完全未知犹豫模糊混合集成算子的群决策方法及应用

陕振沛,杨 倩,宁宝权,郭亚丹

(1.六盘水师范学院 数学与信息工程学院,六盘水 553004) (2.厦门大学 信息科学与技术学院,厦门 361005)

犹豫模糊集作为复杂决策信息表达的主要形式,自文献[1]中首次提出以来,该理论便受到广泛关注,国内外学者相继对此展开了一系列研究．通过梳理国内外文献资料发现,对犹豫模糊集的研究主要集中在决策分析方面,也有的应用在聚类分析、模式识别、机器学习等领域[2-4]．文献[5]中提出了一种新的灰色犹豫模糊集合及其灰关联加权与TOPSIS决策方法．文献[6]中提出了几种新的犹豫模糊集之间的距离和相似性度量．文献[7]中提出了新的犹豫距离集概念,对新型犹豫距离集的特点和经典犹豫距离进行了比较研究,并将其应用于城市道路交通状态的识别．文献[8]中提出了一种基于犹豫模糊交叉熵的协相关度与聚类方法．文献[9]中为解决由犹豫模糊数、直觉模糊数、区间数和实数4类基本数据组成的多源异类数据的融合识别问题,在犹豫模糊框架内,提出犹豫模糊集相关系数计算方法．文献[10]中提出了一种基于符号距离的犹豫模糊多属性决策方法．文献[11]中提出了基于犹豫模糊决策矩阵表示专家偏好的两种关于犹豫模糊多准则群共识决策的方法．犹豫模糊决策信息的集成算子和确定集结信息权重的方法研究是犹豫模糊决策研究的重要内容．国内学者在文献[12-14]中提出的一系列算子上进行推广,定义和构建了众多信息集成算子[15-16]．但是,现有的这些集成算子中绝大多数对决策信息本身或决策信息位置进行集结,同时针对这两者进行集结的犹豫模糊决策信息的集成算子并不常见．还有,通常在做群决策时,要么直接给出了属性权重和专家权重,或者属性权重和专家权重只给出其中的一个,需要求出另外一个,主观性比较强,不能很好地反映决策者的偏好及属性的相对重要性．目前针对权重完全未知的犹豫模糊环境下群决策问题的研究并不多见,因此,文中在犹豫模糊数环境下,提出了一种新的犹豫模糊决策信息的混合加权集成算子,该算子能同时对犹豫模糊决策信息的大小和位置进行加权处理．还给出了新的犹豫模糊熵和犹豫模糊指数熵公式．针对评价属性权重和专家权重信息完全未知的情形,构建了权重完全未知犹豫模糊混合集成算子的群决策方法．并将该方法应用在应急救援路径选择问题上,通过该算例的分析与研究,表明该模型和方法的有效性、合理性和可行性．

1 犹豫模糊集及其混合加权集成算子

犹豫模糊集作为模糊集的一种推广形式,允许元素到某个集合的隶属度用[0,1]中多个可能的取值来表示．这使得人们能够更好地表达对不同目标的偏好的犹豫度．犹豫模糊集的定义:

定义1[1]设X为一给定的集合,犹豫模糊集是从X到[0,1]的一个子集A的映射函数,可以用式(1)来表示,即

H={〈x,hA(x)〉|x∈X}

(1)

式中,hA(x)为[0,1]中几个可能的数的集合,表示x∈X属于X的子集A的可能的程度．

为方便起见,文献[15]中将h=h(x)称为一个犹豫模糊数,它构成了犹豫模糊集的基本组成部分．

有序加权平均算子自1988年Yager提出以来,便得到了广泛的推广和应用,出现了各种不同环境下不同类型的信息集成算子．Xia和Xu在Yager的基础上,依据犹豫模糊集的运算法则提出了犹豫模糊决策信息的一系列集成算子．下面给出犹豫模糊环境下推广最多且应用最为广泛的犹豫模糊加权算术平均(hesitant fuzzy weighted average,HFWA)算子和犹豫模糊加权几何平均(heistant fuzzy weighted geometric,HFWG)算子的定义．

(1) HFWA算子为映射HFWA:Hn→H,使得

(2)

(2) HFWG算子为映射HFWG:Hn→H,使得

(3)

假定犹豫模糊决策信息的权重向量β=(β1,β2,…,βn)T,现同时对犹豫模糊决策信息本身及其位置顺序进行加权,作标准化处理之后,则可以得到一种新的犹豫模糊混合加权算术平均(hesitant fuzzy hybrid weighteed average,HFHWA)算子．

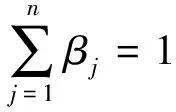
(4)

式中,ε:{1,2,…,n}→{1,2,…,n}为一个排列，使得hj为犹豫模糊数列hj(j=1,2,…,n)中第ε(j)大的元素．

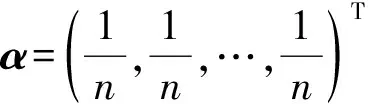
2 犹豫模糊集的熵与指数熵

对于不同的犹豫模糊数,它们中所包含的元素可能是杂乱无序的,另外,所包含元素的数目也可能不尽相同．文献[15]中首先假定犹豫模糊数中的元素按照从小到大的顺序进行排列,同时还假定所有的犹豫模糊数所包含的元素个数相同,基于这两个假设,文献[17]中在模糊熵定义的基础上给出了犹豫模糊熵的定义,即

定义4[17]设h={γσ(1),γσ(2),…,γσ(n)},h1={γ1σ(1),γ1σ(2),…,γ1σ(n)}和h2={γ2σ(1),γ2σ(2),…,γ2σ(n)}为给定集合X上的3个犹豫模糊数,且l=l(h)=l(h1)=l(h2),称实函数E:H→[0,1]为犹豫模糊熵,如果它满足以下准则:

(1)E(h)=0,如果h={0}或h={1};

(2)E(h)=1,如果对任意的i=1,2,…,l,有γσ(i)+γσ(l-i+1)=1成立;

(3)E(hc)=E(h);

(4)E(h1)≤E(h2),如果对任意的i=1,2,…,l,

① 当γ2σ(i)+γ2σ(l-i+1)≤1时,有γ1σ(i)≤γ2σ(i)成立;

② 当γ2σ(i)+γ2σ(l-i+1)≥1时,有γ1σ(i)≥γ2σ(i)成立．

文献[17]中的犹豫模糊熵是在假定所有的犹豫模糊数所含的元素个数相同的条件下给出的,这定义存在一定的不合理和缺陷．例如,倘若两个犹豫模糊数所含的元素个数不同,则只能根据悲观准则和乐观准则,添加一些元素使这两个犹豫模糊数的长度一致，具有相同的元素个数,这样操作本身就会影响犹豫模糊数的自身属性,改变原始的决策信息．因此,文中在文献[17]的基础上对犹豫模糊熵的定义进行改进,使其能够具有普适性,能处理犹豫模糊数具有不同元素个数的情形．

定义5设X为一给定的集合,令h(xi)={γi1,γi2,…,γili}为一个犹豫模糊数,其中,γik(k=1,2,…,li)为xi∈X到另一给定集合的可能的隶属度,li为h(xi)所含值的数目,则：

(5)

为犹豫模糊数h(xi)的犹豫模糊熵．

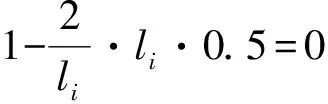
所以0≤E(h(xi))≤1．

证明E(h(xi))满足犹豫模糊熵准则(1～4).

准则(1)的充分性证明：

因此,当h(xi)={0,1}时结果显然成立．

准则(1)的必要性证明：

0≤| 2γik-1|≤1,则对∀γik∈h(xi)都有|2γik-1|=1,从而当γik=0或γik=1时,有:

h(xi)={0}或h(xi)={1}或h(xi)={0,1}．

准则(2)的充分性证明:

准则(2)的必要性证明:

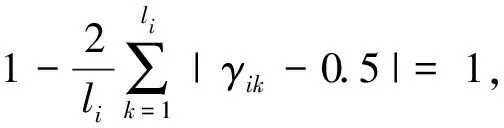
综上所述,E(h(xi))满足犹豫模糊熵的4条准则,从而得证．

因此,文中所定义的犹豫模糊熵E(h(xi))满足文献[17]中所给的犹豫模糊熵的所有准则．

犹豫模糊集的指数熵是在模糊集指数熵的基础上,将其拓展到犹豫模糊环境下,进行新的熵的测度．本文在文献[17]中出的犹豫模糊集指数熵定义的基础上,对其进行改进,提出一种新的犹豫模糊指数熵的公式．

定义6设X为一给定的集合,令h(xi)={γi1,γi2,…,γili}为一个犹豫模糊数,其中,γik(k=1,2,…,li)为xi∈X到另一给定集合的可能的隶属度,li为h(xi)所含值的数目,则犹豫模糊数h(xi)的犹豫模糊指数熵定义为:

(1-γik)eγik-1]

(6)

同样,文中所定义的犹豫模糊指数熵E1(h(xi))满足文献[17]中所给的犹豫模糊熵的所有准则．犹豫模糊指数熵相对犹豫模糊熵更能反映犹豫模糊数熵之间的差异,区分度更高．

下面通过一个例子来说明文中定义的犹豫模糊熵、犹豫模糊指数熵同文献[17]中定义的犹豫模糊熵、犹豫模糊指数熵间的差别．

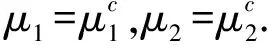
利用文献[17]中定义的犹豫模糊熵和犹豫模糊指数熵公式分别来计算μ1、μ2的犹豫模糊熵和犹豫模糊指数熵,得E(μ1)=E(μ2)=1,E1(μ1)=E2(μ2)=1．然而,从直觉上看,μ2的熵应该要大于μ1的熵,基于文献[17]中给的定义和计算公式不能把μ1与μ2区分开来．利用文中提出的犹豫模糊熵和犹豫模糊指数熵公式计算可得E(μ1)=0.600 0,E(μ2)=0.933 3,E1(μ1)=0.767 2,E2(μ2)=0.993 6,μ2的犹豫模糊熵和犹豫模糊指数熵都比μ1大,能够很好地把μ1、μ2区别开来．因此,当犹豫模糊数同它的补集相等时,文中所提的犹豫模糊熵、犹豫模糊指数熵间的定义和计算公式比文献[17]中所给的要优越,更加合理,能够很好地反映犹豫模糊数熵之间的差异．

3 权重完全未知犹豫模糊混合集成算子的群决策方法

3.1 决策问题描述

3.2 决策方法与步骤

权重完全未知犹豫模糊混合集成算子的群决策方法具体决策步骤如下:

②通过高分辨率卫星数据在生态清洁小流域建设规划审批中的应用，初步构建了遥感技术应用技术流程，对规划设计部门形成了有效的监督机制，为专家评审提供了科学、合理、严谨的参考依据，规范了治理工程的规划、设计、评审等技术环节，保障了生态清洁小流域治理工程设计的合理性。

步骤1:决策者和评价属性权重向量的确定．

(7)

(8)

利用熵最小化原则和犹豫模糊指数熵确定评价属性的权重向量[18],计算为:

(9)

i=1,2,…,m,j=1,2,…,n

(10)

(11)

步骤4:计算各总体值zi(i=1,2,…,m)的得分函数值s(zi)[15]

(12)

式中：lhi为zi中所含元素的数目．通过比较得分函数值s(zi)的大小，对备择方案Ai(i=1,2,…,m)进行排序和优选,得分函数值越大说明方案越优．

4 算例分析

突发事件应急管理是当前有待深入研究的热点问题．设某城市某地方突发大火,城市消防部门立马派出若干消防车辆和救援人员前去火灾现场救援．现有3条救援线路Ai(i=1,2,3)可到达火灾现场,现对这3条救援线路进行评价选择,确定出最优救援路线．所考虑的评价指标包括车辆行驶路程C1、车辆平均速度C2和交通畅通可靠程度C3这3个最主要因素．假设有来自不同部门的3位专家参与火灾应急救援决策,这里评价属性权重和专家权重信息完全未知,每位专家根据自己的专业知识、经验和掌握的资料信息给出每条救援线路对评价指标的犹豫模糊决策矩阵,结果如表1～3[19].

表1 第1位专家给出的犹豫模糊决策矩阵H(1)

注：C1为车辆行驶路程；C2为车辆平均速度；C3为车辆可靠程度.下同

表2 第2位专家给出的犹豫模糊决策矩阵H(2)

表3 第3位专家给出的犹豫模糊决策矩阵H(3)

分别利用式(5、6)求出3位专家给出的犹豫模糊决策矩阵中各救援路线下各属性的犹豫模糊熵和犹豫模糊指数熵,计算结果如表4～6.

表4 犹豫模糊熵与犹豫模糊指数熵矩阵EH1

表5 犹豫模糊熵与犹豫模糊指数熵矩阵EH2

表6 犹豫模糊熵与犹豫模糊指数熵矩阵EH3

根据表4～6求得犹豫模糊熵矩阵,将它们代入式(7)即可求得犹豫模糊决策矩阵的均熵,其值分别为E1=0.711 1、E2=0.688 9和E3=0.688 9．将E1、E2与E3值代入式(8)可分别求出决策专家的权重,决策专家的权重向量为:

λ=(0.317 1,0.341 5,0.341 5)T

通过表4～6求得的犹豫模糊指数熵矩阵和求得的决策专家的权重向量可得到:

P1=0.927 4,P2=0.775 5,P3=0.901 0

将P1、P2和P3值代入式(9)可分别求出评价属性的权重,评价属性的权重向量为:

w=(0.183 3,0.566 8,0.249 9)T

分别计算群体犹豫模糊决策矩阵H=(hij)3×3中每行犹豫模糊数的得分函数,进而确定ε(ij)(i=1,2,3,j=1,2,3),依据犹豫模糊数得分函数式 (12)可得:

s(h11)=0.478 7,s(h12)=0.507 0,s(h13)=0.492 3

s(h21)=0.782 5,s(h22)=0.754 3,s(h23)=0.638 2

s(h31)=0.401 1,s(h32)=0.412 0,s(h33)=0.686 6

由上述可得:h12>h13>h11,h21>h22>h23,h33>h32>h31．于是有:ε(12)=1,ε(13)=2,ε(11)=3;ε(21)=1,ε(22)=2,ε(23)=3;ε(33)=1,ε(32)=2,ε(31)=3．

利用HFHWA算子对群体犹豫模糊决策矩阵H=(hij)3×3中每一行各不同属性值进行集结,这里各属性值集成相关的权重向量，记α=(0.4,0.3,0.3)T,根据式(11)计算各救援路线Ai(i=1,2,3)的总体值zi

z1={0.465 8,0.472 3,0.473 8, 0.480 2, 0.483 4,0.489 7, 0.491 2, 0.497 3, 0.503 4, 0.509 4, 0.510 9,0.516 8, 0.519 8, 0.525 6,0.527 0,0.532 7}

z2={0.679 6, 0.685 3,0.686 9, 0.692 5,0.695 4, 0.700 8,0.702 4, 0.706 1,0.707 7, 0.711 4,0.712 9, 0.718 0, 0.720 6, 0.725 6,0.727 0, 0.731 9, 0.756 1,0.760 4, 0.761 7,0.765 9,0.768 1, 0.772 2,0.773 4, 0.776 3, 0.777 5, 0.780 3,0.781 4, 0.785 3, 0.787 3, 0.791 1,0.792 2,0.795 9}

z3={0.463 6, 0.468 4, 0.468 8, 0.473 5, 0.480 8,0.485 4, 0.485 9, 0.490 4, 0.491 7, 0.496 2, 0.496 6, 0.501 1,0.508 0, 0.512 3,0.512 8, 0.514 6, 0.517 1,0.518 9, 0.519 4, 0.523 6, 0.530 2, 0.534 4, 0.534 8, 0.538 9, 0.540 0, 0.544 1, 0.544 5, 0.548 5, 0.554 8,0.558 8, 0.559 1,0.563 0}

分别计算zi(i=1,2,3)的得分函数值s(zi)(i=1,2,3),根据犹豫模糊数得分函数式 (12)可得:

s(z1)=0.500 0,s(z2)=0.741 5,s(z3)=0.515 0

由s(z2)>s(z3)>s(z1)可知,z2>z3>z1,因此,A2≻A3≻A1,救援线路A2为最优路径选择,A3次之．

下面对表3中第3位专家给出的犹豫模糊决策矩阵H(3)中救援线路A2在属性C1、C2、C3下的值做一下变动,对应的属性值分别变为{0.6,0.8}、{0.7}、{0.6,0.7},其他各值不变,按照同样的方法和步骤计算得到s(z1)=0.508 6,s(z2)=0.751 2,s(z3)=0.523 5．因为s(z2)>s(z3)>s(z1),所以可得A2≻A3≻A1,这与上面得出的结论完全一致．也就是说,虽然第3个决策者稍微改变了他的偏好,但是决策结果仍能保持一致,该算法在实际应用中具有鲁棒性．

采用文献[16] 中提出的拟犹豫模糊有序加权算术平均算子得到的排序结果为A2≻A3≻A1,与文中结果一致.在决策信息集结过程中，文中提出的方法计算量比拟犹豫模糊有序加权算术平均算子小．采用文献[20]中提出的最大一致性模型确定专家的权重信息,利用TOPSIS方法对方案排序择优的结果仍为A2≻A3≻A1．但最大一致性模型需要属性权重已知,而文中得出的综合评价值之间差异相对要小些,具有良好的区分度,更能体现决策者行为特征和决策过程中的柔性．

5 结论

文中旨在犹豫模糊环境下,针对评价属性权重和专家权重信息完全未知的情形,提出一种合理有效的群决策方法,在决策方法及理论上有所创新,文中主要做了以下几个方面的工作:

(1) 提出了一种新的犹豫模糊决策信息的混合加权集成算子,它能够同时对犹豫模糊决策信息本身及其顺序位置进行加权;

(2) 提出了一种新的犹豫模糊熵和犹豫模糊指数熵公式,分别用来确定决策者和评价属性的权重向量．通过查阅文献资料发现,通常在做群决策时,要么直接给出了属性权重和专家权重,或者是属性权重和专家权重只给出其中的一个,需要求出另外一个,主观性比较强,相比文中求取权重方法更加合理,更加合理地描述决策者的偏好及属性的相对重要性,适用性和应用性更强;

(3) 将权重完全未知犹豫模糊混合集成算子的群决策方法应用在应急救援路径选择问题上,丰富和发展了应急决策理论与方法．