基于电子地图的改进蚁群算法及其车辆路径寻优

刘庆华,汪 晶

(江苏科技大学 计算机学院, 镇江 212003)

随着科学技术和经济迅猛发展,现实生活中车辆普及率越来越高,汽车私人拥有量也快速增加.交通事故、交通拥堵等问题频繁出现,使得出行者迫切需要正确的出行路径来尽可能避免类似事情发生.因此，路线规划问题成为了国内外学者研究的一项重要课题[1]．国内外学者对路径规划问题进行了大量研究,早期研究主要集中在理论及算法方面,具有重要应用价值,比如在旅游业和物流业等行业中，合理的路线规划能够为商家节约成本,创造更高价值[5]．

文献[7]中首次提出了物流配送路径优化问题,之后,便引起了计算机应用等诸多领域的研究者们的高度关注,且迅速成为了运筹学和组合优化领域的研究热点和前沿问题，从而使得学者们对上述问题进行了大量理论研究和实验分析,并获得了较大的进步和成果．文献[8]中提出了蚁群系统(ant colony system,ACS),它是一种应用于旅行商问题(travelling salesman problem,TSP)的分布式算法,也就是通过ACS算法研究路径规划问题,通过ACS算法和模拟退火算法等进行比较，表明ACS算法理论上能更好解决TSP问题．文献[9]中针对大型货柜在建筑工地及购物区堆积大量垃圾,提出了一种滚动式废物收集车辆路径优化问题．文献[10]中研究了冷藏车和一般车辆在多种类易腐食品运输过程中的路线规划问题．文献[11]中做了基于仿真的交通拥堵车辆路径规划问题研究,将交通拥堵转化为非确定性动态模型,首次将上限置信区间算法(upper confidence bound apply to tree,UCT)应用在动态交通问题之中,并与蚁群算法进行了比较,为文中方法的跨域适用性带来了希望．文献[12]中建立了带约束条件的物流配送问题的数学模型, 运用蚁群算法解决物流配送路径优化问题, 同时将遗传算法的复制 、交叉和变异等遗传算子引入蚁群算法, 以提高算法的收敛速度和全局搜索能力．文献[13]中提出了一种改进的蚁群算法，应用于物流网络中,并通过澳大利亚邮政数据进行选址仿真实验,验证了该算法模型在应用中的求解效率和计算稳定性．文献[14]中针对救援关键期内应急物资可能供应不足的特点,考虑适当的优化目标,建立了随机需求环境下应急物流车辆路径问题的优化模型,并基于遗传算法设计了模型的求解方法．

对于车辆路径优化问题求解,上述研究以节点之间的线性距离之和最短作为最优解,但是在实际的道路中节点之间会存在诸多因素(如道路单向行驶、道路弯曲等)，使得以节点之间的线性距离最短作为求解结果难以运用在实际需求之中．文中以镇江市实际物流配送路径合理规划为出发点,通过高德电子地图提供的对应API接口来获取各个节点之间的实际道路导航距离,然后通过改进蚁群算法进行优化求解,从而将理论与实际物流配送路径结合,具有高度的可行性和实用性．

1 物流配送数学模型

1.1 配送过程介绍

物流配送过程可以描述为从物流配送站通过一定数量的车辆分别向若干个客户节点派送货物,车辆配送完货物后则返回物流配送站．每辆车辆的载货量有限,为了节约成本以及提高派送货物的效率,则必须合理规划车辆配送路线,使总行驶路程最短．

1.2 数学模型建立

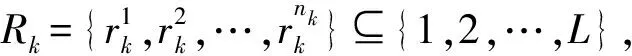
(1) 某一个节点的货物需求只能由一辆车辆来配送;

Rk1Rk2=Φk1≠k2

(1)

(2) 任意一条路径上的节点需求总量之和不能超过汽车的载重量Qk;

(2)

(3) 所有节点都必须完成配送

0≤nk≤L

(3)

(4)

(5)

因此,文中的物流配送问题需要达到的最优路径理论目标值为:

(6)

2 基本蚁群算法

2.1 基本原理

蚁群算法是受自然界蚂蚁觅食行为启发而产生的一种自然模拟进化算法[15]．文献[16]中首次阐述了蚁群算法,并对其数学模型做了分析解释．蚂蚁从蚁穴到目的地的觅食过程描述如下:起初，蚂蚁随机选择路径,后来路径选择会根据觅食过程而搜索新路径,原因在于蚂蚁会在它们经过的地方释放一种化学物质(信息素),而这种化学物质的浓度与路径长度有关,走过路径越长,它的浓度相对越低,同时路径上的该化学物质的量也会随着时间的流逝按照一定的比例逐渐减少,因此对于较短的路径上蚂蚁释放的信息素浓度会更高,如此反复形成正反馈效应,直到最后所有的蚂蚁都会走信息素浓度最高的那条路径,也就是最短路径．关于蚂蚁觅食过程的简要流程图如图1．其中(a)表示所有蚁群都在起点处,路径上尚未有信息素；(b)表示蚁群开始分别以相等的概率向不同的方向觅食；(c)表示走较短路径的蚁群首先到达觅食终点；(d)表示蚂蚁返回起点过程中由于较短路径上信息素浓度较高,所以蚂蚁选择较短路径的概率要大于较长路径的概率,最终根据正反馈效应蚂蚁都会集中在较短路径上[17]．

图1 蚁群觅食行为(单位：m)Fig.1 Ant colony foraging behavior map(unit:m)

现实生活中，人工蚁群算法根据蚁群觅食的正反馈过程实现,在自然界的蚁群算法上作了改进.原始自然界中，蚁群是没有记忆功能的,而人工蚁群算法具有一定记忆功能,它会记住已经访问过的节点．另外，人工蚁群算法会根据算法规律去选择下一条最短路径,它并非无目的性地选择下一条路径．

2.2 求解模型

当蚂蚁在客户点i时,它在t时刻由客户点i向客户点j转移的概率为:

(7)

式中：ηij，τij分别为某时刻客户点i到客户点j的可见度以及i到j路径上的信息素浓度,且ηij=1/dij;α为信息启发因子,β为期望启发因子,大小分别对应蚂蚁对信息素量和路线距离长短的敏感程度;由于每只蚂蚁每次巡回只能访问客户节点一次,所以用tabu(k)表示第k只蚂蚁已经访问过的节点,allowed(k)=R-tabu(k)表示第k只蚂蚁还没有访问的节点．

当所有的蚂蚁完成一次配送循环后,需要根据各个蚂蚁遍历的好坏程度,更新相关路径上的信息素,因为信息素是影响文中算法收敛性的重要因素,相关路径上信息素的更新规则:

τij(t+n)=(1-ρ)τij(t)+Δτij(t)

(8)

(9)

式中：ρ为信息素挥发系数,0≤ρ<1,1-ρ为信息素残留系数;Δτij(t)和τijk(t)分别为这一次循环过程中i到j路径上所有的信息素增加量和第k只蚂蚁留在路径上的信息素数量;m为该循环过程中蚂蚁数量;τij(t+n)和τij(t)分别为对应时刻路径上的信息素数量．最后在上述基础上得到蚁群算法的基本求解模型:

(10)

式中：Q为常数,表示信息素强度,它在一定程度上会影响算法的收敛速度;Lk为第k只蚂蚁在本次循环中走过的路径总长度[18]．

3 蚁群算法改进及其物流配送

3.1 客户节点选择策略改进

如图2,假设蚂蚁经过A,B,C点运动到了D位置,在D位置蚂蚁可以选尚未去过的E,F,G中任意一点作为下一个访问节点,且D点到E,F,G这3点的距离/信息素分别是2/2,5/2,3/3．根据式(7)，在α=1,β=2的条件下可计算得到从D点到E,F,G这3个节点的概率分别为24%,60%和16%．因为D到F的概率值大于D到其他点的概率值,所以蚂蚁自然选择F点作为下一个访问节点,同样，在蚂蚁选择其他节点时也会出现类似情况,这样全部蚂蚁选择的路径是相同的,使算法陷入停滞状态．采用轮盘选择策略可以很好解决这一问题,首先在[0,1]之间随机取一个数R,然后用R减去D到E路径上的概率,倘若得到的结果≤0，则E点即为下一个访问节点,否则将得到的结果继续减去D到F路径上的概率,以此类推直到得到的结果≤0时将对应的点作为下个一访问节点．通过采用这种策略可以有效避免算法停滞或陷入局部最优解,因为这种方式在蚂蚁选择下一个访问节点时不会总往概率大的路径上走,而是向概率大的路径上走的可能性更大,但是依然有可能向概率小的路径上走．

图2 蚂蚁简略寻迹Fig.2 A simple trace of ants

3.2 信息素挥发系数ρ取值改进

信息素挥发系数ρ是一个常量,它的取值直接影响算法的求解结果,若ρ值过小,则影响算法的收敛速度,取值过大,则会使没有被搜索过的路径被选择的概率减小,影响算法的全局搜索．所以在求解过程对ρ值进行调整,在算法初期为了尽快找到较优解，ρ值应比较大;到了后期当算法停滞不前就可以将ρ值减小,减小信息素对蚁群的影响,取得更优解．ρ值调整公式如下:

(11)

式中：r为循环次数;rmax为一常量;μ∈(0,1),也是一个常量,用来掌握ρ的衰减速度;ρmin为ρ的最小值,确保ρ不会因为过小而影响收敛速度．这里当r达到设定的rmax时就减小ρ,然后对r重新计数,反复循环,直到ρ达到最小值ρmin为止[19]．

3.3 改进客户节点间距离计算方式

本算法中计算最优路径时去掉基本的蚁群算法通过传统方法来计算任意两个节点间距离,而是通过程序调用高德地图Web服务API接口，返回任意两个节点间实际导航距离，求得最优解．

程序中计算任意两个节点距离的接口服务地址为https:∥restapi.amap.com/v3/distance?parameters.接口的请求参数包括key(请求服务权限),origins(出发点),destination(目的地),type(路径计算的方式和方法),output(返回数据格式类型xml或json,文中取json),callback(回调函数).文中，上述请求参数tpye直接取缺省值,表示驾车导航距离．返回结果参数包括status(0表示请求失败,1表示请求成功)、info(返回状态说明)、result(距离等信息列表)．这里得到的任意两个客户节点之间的距离是实际道路之间的有向距离,而不是传统方式所采取的根据勾股定理来计算的直线距离,而且通过接口在不同时间段取得的值不同,因为服务接口中考虑了实时路况,躲避了交通拥堵等．

3.4 物流配送流程

物流配送的具体流程如下：首先，确定车辆数以及客户点信息；随后，计算车辆下一时刻对每条路径的选择概率，从而确定下一个即将访问的客户点，并根据规则对前文中的ρ值进行改进，满足条件后返回，依次遍历每辆车；最后，根据每辆车的最优选择结果得出最合适的配送方案.流程图如图3.

图3 物流配送算法流程Fig.3 Algorithm flowchart of logistics

4 实验结果与分析

4.1 问题描述

物流配送以镇江市实际道路点为基础,分别向本市10个不同的客户点进行物流配送,寻求最优的配送路径．这里以镇江站位置为物流配送中心,以十里长山、镇江南站、江苏大学、江科大东校区、大港中学、明都大饭店、金山公园、中医院、江大附属医院、八佰伴为客户点位置．物流配送中心车辆充足,且每辆车载质量为8 t,10个客户点的需求量qi如表1,现在要求合理安排车辆及规划路线,使配送过程的总路程最短．由表1可知10个客户节点总需求量为29.4 t,而每辆车的载质量为8 t,初始估计配送车辆为4辆．

表1 客户点需求量

另外上述算法中参数α值过大，搜索路径的随机性会减弱,过小的话会陷入局部最优;β值过大容易选择局部最短路径,过小算法收敛速度太低,通过计算分析文中信息启发因子α和期望启发因子β的取值，分别定为1和2;初期为了尽快找到最优解，信息素挥发系数ρ取0.95,算法后期根据实际情况对ρ值进行调整;迭代次数为200．

4.2 结果与分析

通过高德地图服务API得到的物流配送中心与各个客户点以及客户点和客户点之间的实际道路距离如表2．其中(0,0)表示物流配送中心,1～10表示10个客户节点,由表2中可知dij和dij距离不相等,这是因为表2中所有节点之间的距离都是根据API接口取得的实时驾车导航距离,而不是传统的道路节点之间的直线距离．另外程序在取得道路节点间的实际距离时可以根据接口传参考虑诸多因素,如实时路况,是否躲避交通拥堵路段,还是不考虑路况直接走最短路线路段,以及不走高速且避开收费等,通过高德地图API取得实际道路距离后，再使用蚁群算法求得最优解．

表2 各节点之间的实际道路距离

物流配送路径的优化结果对比如表3,表中列出了具有代表性的10次配送路径、对应的根据传统方式得到的节点间直线行驶路程和根据实际道路行驶得到的行驶路程．由表3可知节点间最小直线行驶路程的最优解为62.598 km,但是与其对应的节点间的实际道路行驶路程却不是最小的,而表中第5行所对应的路径得出的实际道路行驶路程89.378 km才是最小值．这充分说明了在实际应用中,最优路径求解过程中根据节点间的直线距离来计算最小路程是难以解决实际问题的,应该根据文中提出的由实际道路节点距离来计算最优路径,这样才能得到实际的最优解．这里由于文中提供的客户点较少且距离比较近,所以不同路径所对应实际道路行驶路程相差不是太大,但是在客户点较多或客户点之间相距比较远时,这种差距就会十分明显,且更能体现由实际道路距离作为最优路径求解结果的正确性与优越性．

在算法收敛性方面,文中的最优解在迭代40次以上基本上已经趋于稳定,迭代过程中平均路径长度和最短路径长度如图4．

表3 路径优化求解结果对比

图4 路径优化结果收敛Fig.4 Convergence graph of path optimization result

最后,在实验中根据传统蚁群算法和文中改进的蚁群算法，同样在迭代200次的基础上，以及在相同约束条件下,对比直线最短路程、平均路程和最大路程，如表4．可知文中改进算法相比于未改进之前增强了算法的正反馈机制,避免了算法停滞现象,对路径规划问题具有较好的适应性和实用性．

表4 算法改进前后数据对比

5 结语

文中从物流配送路径优化问题出发,以镇江市实际道路节点为基础,通过改进的蚁群算法来求得配送过程中所走的实际道路节点的最短路程．在前人研究基础上,文中求得的最优路径并非通过节点间直线行驶最短距离来求得,而是通过高德API服务接口获取各道路节点之间的实时导航距离，并由改进的蚁群算法求得最优解．实验结果证明,传统求解方式难以应用于实际,而文中提出的求解方式在实际应用中具有更好的应用价值,实用性更高．