单折线体外索对简支钢梁自振频率的影响
2020-03-30李红明唐柏鉴
王 飞,李红明,唐柏鉴.3,陈 淞
(1.江苏科技大学 船舶与海洋工程学院, 镇江 212003) (2.江苏科技大学 土木工程与建筑学院, 镇江 212003) (3.苏州科技大学 土木工程学院, 苏州 215009)
体外预应力技术是后张法预应力技术的重要分支之一,采用体外预应力技术不仅能减小构件截面尺寸、降低用钢量,还能提高结构承载力,因此应用越来越广泛[1-2].目前,对体外预应力钢结构的静力性能研究较多,但对其动力性能的研究还不够深入.研究体外预应力梁振动特性的目的,主要是因为预拉力会影响结构自振频率,在设计预应力结构时,为防止共振影响使用,需要确定合理的预拉力参数.
通常,将预应力索看成作用于梁端的一对压力F,根据经典理论得到简支梁弯曲振动时的自振频率[3]为:
(1)
式中:i=1, 2, 3,…;l为梁的跨长;E为钢材弹性模量;I为钢梁截面惯性矩;m为单位长度梁的质量.对比无预拉力时简支梁的自振频率公式可见,预拉力的存在使梁的弯曲自振频率减小,称为“压缩软化效应”[4-6].但是通过对预应力混凝土梁的研究发现,体外预应力梁不同于体内预应力梁,体外索作为结构中一个独立构件,振动时受到梁体的约束较少,对体外布索梁,把预应力系统等同于作用在梁端的轴压力这一做法值得商榷[7].文献[8]通过试验和有限元计算发现预应力索的预拉力、偏心距和布置都对钢梁自振频率有影响.很多学者分别采用刚度修正法[9]、非线性动力分析法[10]、等效刚度法[11]等方法探究了预应力参数对自振频率的影响.值得注意的是,人工神经网络的应用[12]也为探索梁的动力性能提供了一条新的路径.
为方便工程设计时确定体外单折线布索预应力钢梁的自振频率,文中从预应力系统作用机理的角度出发,采用能量法推导了简支梁的自振频率计算公式,后用ANSYS有限元软件对典型单折线布索钢梁的自振频率进行数值计算,并将计算结果与公式得到的结果对比,以验证公式的正确性.此外,还探究了索预拉力大小、偏心率和截面积三者对此类预应力钢梁自振频率的影响规律.
1 基于预应力系统作用机理的钢梁自振频率理论分析
1.1 体外预应力系统的作用机理
在预应力钢结构体系中,预应力系统由预应力及施加预应力的载体组成.体外预应力钢结构中的预应力系统其作用机理主要概括为以下三种[13]:
(1) 为结构构件提供反向力及变形且影响结构频率,如拉索拱结构、张弦梁结构等.
(2) 预应力拉索增加结构整体刚度.预应力索自身有轴向抗拉刚度,该刚度与预拉力大小无关,是结构刚度的重要组成部分,如索支撑结构、斜拉结构等.但柔性拉索无轴向抗压刚度.当拉索拉力为零,轴向抗压刚度也为零,此时,结构整体刚度发生突变.预拉力的存在可使拉索推迟退出工作.
(3) 为结构构件提供弹性约束支承,并增加结构整体稳定性.当预应力拉索发生垂直于索轴线的变形时,结构产生附加内力,形成轴力的二阶效应,此二阶效应为拉索提供刚度,如点支式幕墙结构、弦支结构等.
1.2 体外预应力钢梁自振频率的计算公式
基于上述机理,现从能量角度推导单折线布索预应力钢梁的自振频率.推导过程中采用的基本假设与经典结构动力学一致,且为满足能量法的使用条件并使公式尽量简化,增加以下三条假设:(1) 简支梁第i阶振型的振动方程与经典结构动力学中解析解形式一致,设为yi=y0isin(iπx/l)sin(ωit+φi),i=1,2,3,…(以钢梁左端为原点,梁轴线为x轴,y0i、ωi和φi分别为圆频率振幅和相位角).(2)忽略梁的轴向变形.(3)施加预拉力后梁为直线.
为了不失一般性,设钢梁为工字形截面,预应力索除在梁两端锚固(偏心距为e)外,在跨中与钢梁下翼缘附件锚固使拉索呈折线状态,此外不与钢梁接触,如图1,图中θ为预应力拉索与水平方向所成的夹角,F为索的预拉力大小,在小变形振动中忽略其值的变化.

图1 单折线布索钢梁示意图Fig.1 Prestressed steel beam with fold-line tendons
第i阶振动中,梁体的最大动能为:
(2)
式中:mB为单位长度梁体质量.因跨中拉索锚固点的竖向运动速度即为此处梁的横向振动速度,忽略拉索自身的微小横向振动,任意时刻位置x处拉索的竖向速度可近似为:
(3)
则拉索最大动能为:
(4)
式中:mT为单位长度索的质量.预应力梁的最大动能为梁体和索两者最大动能之和.
当梁挠度最大时,其势能最大,势能包括梁体弯曲势能、索作为弹性支座的拉伸势能及梁跨缩短所引起的索势能减小.微小变形时,将拉索近似为偏心距(e+e′)/2的直线索,如图2.

图2 单折线布索钢梁的横截面Fig.2 Cross-section of prestressed steel beam with fold-line tendons
忽略梁体和索两者弹性模量的差异,定义预应力梁截面的等效惯性矩为:
(5)
式中:I0为梁体截面惯性矩,AT为索截面积.梁体等效弯曲势能最大值为:
(6)
由于索、梁在跨中耦合,与不耦合的布索方式相比[14],拉索会产生垂直于索轴线的位移使其势能增大.将拉索及锚固附件看成设在梁跨中的弹簧支座,并忽略索拉力二阶效应造成的刚度,得其刚度贡献为:
(7)
值得注意的是,当为偶数阶振动时,跨中梁截面的挠度为零,此时索为梁体提供的支承刚度k也为零.因拉索起支承作用而产生的弹性势能最大值为:
(8)
预应力钢梁跨长缩短引起的拉索势能增量最大为:
(9)
不计阻尼,预应力梁的最大动能总等于它的最大势能,结合式(2)、(4)、(6)、(8)及(9),得到方程:
(10)
解此方程得自振频率为:
(11)
其中,

2 有限元法验证
为验证上述公式,用有限元法计算一典型单折线钢梁的自振频率.有限元分析采用的钢梁模型尺寸及布索方式如图3(a),跨长4 m,截面高250 mm,宽120 mm,梁翼缘、腹板均为6 mm厚.为便于固定拉索,在梁两端及跨中设加劲肋,两端加劲肋厚20 mm,跨中加劲肋厚10 mm.拉索呈折线状态,在跨中与梁通过加劲肋耦合,锚固点距梁下翼缘15 mm.采用高强度钢绞线作为预应力索,梁体材料为Q345B钢,材料属性如表1.

图3 预应力钢梁的布索方式及其有限元模型(单位:mm)Fig.3 Elevation of prestressed steel beam and its finite element model(unit:mm)

表1 梁体和预应力索的材料属性
采用ANSYS有限元软件建立预应力钢梁计算模型.钢梁体(包括加劲肋)采用Solid 95实体单元,每根预应力索采用两个Link 10单元模拟,通过节点自由度耦合方法模拟锚固作用,网格划分采用映射方法,如图3(b),令实体单元大小控制在20 mm×20 mm×20 mm以内.模型梁两端简支.梁和索均采用线弹性材料模型.动力分析时,结构刚度应采用有预拉力作用时的结构刚度,因此,采用降温法施加预拉力后先进行静力分析.模态分析中索取不同预拉力、偏心距和截面积,分析它们对梁一阶自振频率的影响,并将计算结果与由式(11)得到的理论值对比.
3 自振频率影响因素分析
3.1 预拉力对自振频率的影响
计算时拉索截面积取139 mm2,偏心距取0,即无偏心.预拉力在0~1 000 kN之间变化,梁的一阶自振频率理论值与模拟值的对比见表2.可见,钢梁一阶自振频率随预拉力增大而减小.当预拉力从0增至1 000 kN时,一阶频率的理论值和模拟值分别降低了5.40%和3.31%.不同预拉力下,理论值与模拟值相比,最大误差仅2.22%.

表2 不同预拉力下预应力钢梁一阶自振频率值
3.2 偏心距对自振频率的影响
分析中预拉力取800 kN,拉索截面积仍为139 mm2.不同偏心距下得到预应力钢梁一阶自振频率理论值及模拟值见表3.从表3可知,预应力钢梁的一阶自振频率随偏心距增大而增大.当偏心距达110 mm时,自振频率理论值相比无偏心时增大了4.53%,而模拟值增大了5.39%.不同偏心距下公式计算结果相对有限元结果误差最大为0.52%,即两者基本吻合.
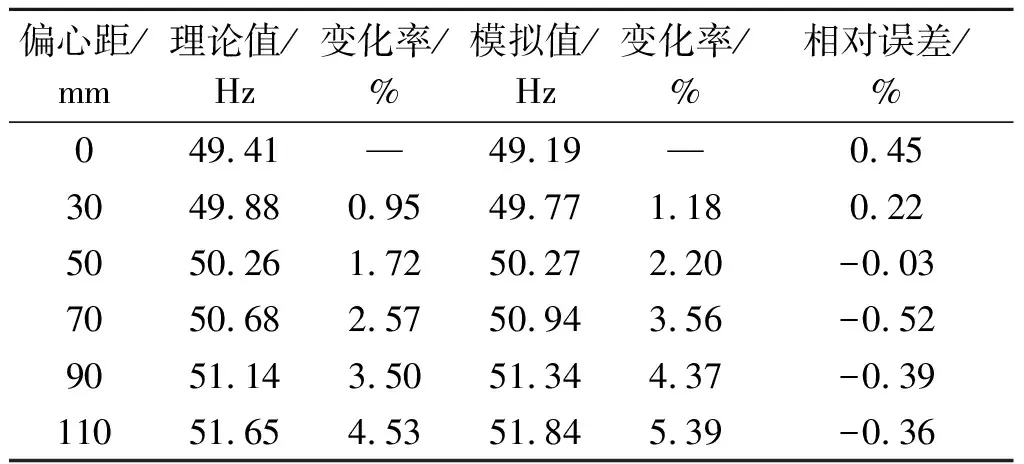
表3 不同偏心距时预应力钢梁一阶自振频率值
3.3 拉索截面积对自振频率的影响
采用不同截面规格钢绞线作为预应力索进行分析,索预拉力取800 kN,偏心距取70 mm,得到预应力钢梁一阶自振频率的理论值及模拟值如表4.表4说明梁一阶自振频率随索面积增大而增大.

表4 不同索截面时预应力钢梁一阶自振频率值
当索面积从54.8 mm2增加到285 mm2,理论值增加了8.79%,模拟值增加了3.81%.可见,索截面积对钢梁一阶自振频率影响较预拉力和偏心距更大.不同索截面积下自振频率理论值与模拟值相比,误差最大仅为2.59%.
4 结论
(1) 用能量法推导的单折线型预应力钢梁自振频率计算公式能简单、快速得出频率值且该公式所得到的一阶频率值与有限元结果基本一致,不仅具有良好的计算精度,且各部分物理意义明确,能为工程应用起到一定参考作用.
(2) 索预拉力、偏心距与截面积三者对单折线型预应力钢梁自振频率均有一定程度影响,因此,可改变这些参数调节梁的自振频率,避免共振.具体来说,钢梁的自振频率随预拉力增大而减小(奇数阶时),随偏心距和截面积的增大而增大.其中,预拉力对自振频率影响最小,偏心距其次,截面积的影响最大.
