基于高分辨率拉东谱的逆时偏移角度域共成像点道集提取

赵 磊,杨勤勇

(中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)

角度域共成像点道集是偏移速度分析和AVA分析的有力工具。传统的计算逆时偏移角度域共成像点道集的方法主要包括局部平面波分解[1-2]、频率-波数域角度分解[3-4]、扩展成像条件类方法[5-8]和坡印廷矢量类方法[9-12],扩展成像条件类方法和波场分解类方法需要耗费巨大的计算和存储资源。

XIE等[1]在时空域对地震波加窗,假设在一定尺度范围内,曲面波近似平面波,将曲面波进行平面波分解得到角度域共成像点道集;YAN等[2]进一步将该方法应用于逆时偏移成像,获得了逆时偏移角度域共成像点道集。SAVA等[7]通过逆时偏移生成偏移距域共成像点道集,然后将偏移距域共成像点道集转化为角度域共成像点道集;李振春等[4]分别利用单平方根算子和双平方根算子波动方程偏移方法提取了偏移距域共成像点道集,并应用插值法将偏移距域共成像点道集投影到角度域,获得角度域共成像点道集;该类方法在三维情况下需要对偏移距域共成像点道集做一个五维傅里叶变换,计算量庞大。XU等[3]提出将逆时偏移中的地震波场保存下来,将其转换到频率-波数域做角度分解求取反射角和方位角以获得角度域共成像点道集,该方法需要巨大的计算量与存储量,实际应用困难。与前面几类方法相比,坡印廷矢量类方法可以高效率、低成本地生成角度域共成像点道集。

YOON等[9]将坡印廷矢量引入逆时偏移成像中,通过控制互相关波场的夹角去除逆时偏移的低频噪声;郭鹏等[13]使用基于坡印廷矢量的互相关成像条件压制层间反射对逆时偏移的影响。DICHENS等[10]利用坡印廷矢量计算炮点波场和检波点波场传播方向提取了逆时偏移角度域共成像点道集;VYAS等[11]和YOON等[12]利用炮点波场的传播方向和反射界面的倾角计算入射角度提取逆时偏移角度域共成像点道集;ZHAO等[14]利用偏移剖面预测反射界面法线方向,结合稳定的炮点波场入射方向计算入射角度提取角度域共成像点道集;王保利等[15]采用一阶波动方程计算坡印廷矢量,进一步减少角度道集提取的计算量;吴成梁等[16]将坡印廷矢量方法和局部平面波分解相结合,在提取角度道集的同时解决波前交叉的问题。

计算波场的入射角度是提取角度域共成像点道集的关键步骤,获得入射波方向、反射波方向和反射界面法线方向三者中的任意两个就能得到入射角度。通过坡印廷矢量方法或者对波场作用一个梯度算子,可以很容易地获得波场的传播方向[17]。由于炮点正传波场相对于检波点逆传波场信噪比更高,因此,我们通过炮点正传波场计算坡印廷矢量作为入射波方向。反射界面的法线方向由叠前深度偏移剖面得到,主要方法有瞬时波数方法[18]、局部倾斜叠加方法、梯度算子方法和希尔伯特变换方法等等。使用这些方法的前提是地下反射界面真实存在,对于无反射界面区域能量投影的问题则无法解决,无反射界面区域不存在反射界面法线方向,计算得出的法线方向是不合理的。

本文提出了一种基于高分辨率拉东谱和反射界面法线方向概率分布的角度域共成像点道集提取方法,使得对于有反射界面的区域其能量能够正确投影,而无反射界面的区域其能量随机叠加压制,从而解决了基于炮点入射波矢量方向和反射界面法线方向提取角度域共成像点道集时无反射界面区域能量投影不准确的问题。

1 方法原理

逆时偏移的成像条件为:

(1)

式中:I(x)为地下各点的像;x为矢量(x,y,z),表示地下各点坐标;Ws(x,t)和Wr(x,t)分别为炮点波场和检波点波场;t表示时间。成像条件中并没有角度相关信息,为了获得逆时偏移角度域共成像点道集,需要对成像条件进行修改,加入角度相关信息,修改后的成像条件为:

(2)

式中:θ(x,t)为地下点x在t时刻的入射角信息。为了获得地下任一时刻的地震波的入射角度θ(x,t),需要计算地震波的入射方向ps、反射方向pr和反射界面法线方向pn中的任意两者。入射方向ps的计算依赖于炮点正向外推的模拟波场,反射方向pr的计算依赖于检波点逆向外推的地表波场,反射界面法线方向pn可以由叠前深度偏移成像剖面获得。

通过入射方向ps和反射界面法线方向pn计算地震波入射角度的方法有以下优点:一是ps通过模拟波场计算得到,模拟波场信噪比高,计算得到的ps准确、稳定;二是pn由偏移成像剖面得到,具有相当高的可信度。相对应地,pr由检波点波场计算得出,而检波点波场是通过地表记录作为边值条件逆时重构得到的波场,只有地表一侧的波场用于检波点波场重构,因此重构之后的波场信噪比低,会影响pr计算的稳定性和准确性。由ps,pn计算的入射角要比由ps,pr计算的入射角更稳定和准确。但是,对于无反射界面区域,pn不存在,直接计算pn不可行,因此本文通过计算地下各点反射界面法线方向的概率分布prob(x,pn)来代替直接计算pn,解决无反射界面区域角度道集的噪声问题。

1.1 炮点波矢量方向的计算

对于地下任一点,单炮波场,其主能量的入射方向是固定的,并且在时间上有一定的延续度,主要是和子波长度相关联。由于我们只需要在主能量到达时附近进行相关成像,可以认为在这个时间区间里,地震波的入射角度是固定不变的,在进行角度投影时,地下每一点只需要计算波场主能量入射该点时的传播方向。

要得到炮点波场主能量的传播方向,一个简单而有效的办法是通过计算坡印廷矢量来获得:

(3)

波场入射到地下某一点时,在主能量到达时刻的一定时间范围内,入射方向不会发生变化,由于震源子波的时间对称性和延续性,在主能量到达时刻之前和之后的半波长范围内,波场的传播方向不会发生改变。也就是说,我们只要叠加主能量到达时刻之后的半波长范围内的坡印廷矢量就可以得到波场对地下各点的主能量入射方向,这样就解决了坡印廷矢量计算的稳定性问题和坡印廷矢量的存储问题,在实际应用中,我们使用公式(4)进行计算。

(4)

式中:ps_cal(x)表示地下各点稳定的主能量入射方向,用于入射角度计算;ps(x,t)表示地下各点t时刻主能量入射方向;tdomi表示主能量到达时;T为子波周期。

1.2 反射界面法线方向概率分布的计算

地下反射界面法线方向概率分布是基于叠前深度偏移剖面的高分辨率拉东谱获得,首先对叠前深度偏移剖面(本文中使用逆时偏移剖面)提取高分辨率拉东谱。

1.2.1 高分辨率拉东谱的提取

为了便于分析拉东谱能量分布的特点,进而提高拉东谱分辨率,我们给定一个子波w(t),对其进行傅里叶变换和余弦变换:

(5)

式中:a(f)表示w(t)的频谱;f表示子波频率;[-fN,fN]为频率积分区间。

对子波w(t)进行一个时移t0得到信号s(t):

s(t)=w(t-t0)

isin[2πf(t-t0)]}df

(6)

接下来,我们构造一个线性信号g(t,x),在坐标原点处其时移量为t0,其传播方向为p0,根据公式(5)和公式(6),该线性信号可表示为:

g(t,x)=s(t+p0x)

isin{2πf[(t-t0)+p0x]}}df

(7)

下面给出线性信号g(t,x)的拉东谱r(τ,p):

{cos{2πf{[(τ-px)-t0]+p0x}}+

isin{2πf{[(τ-px)-t0]+p0x}}}df

(8)

式中:[-X,X]表示x的积分区间,由选定的倾斜叠加范围决定。

公式(8)中,[(τ-px)-t0]+p0x=(τ-t0)-(p-p0)x,当拉东谱上点(τ,p)靠近能量团中心点(t0,p0)时,有:

(isin{2πf{[(τ-px)-t0]+p0x}}≈0

sin[2πf(τ-t0)]≈0

sin[2πf(p-p0)x]≈0

因此,在能量团中心点(t0,p0)附近,公式(8)可以近似地表示为:

(p-p0)x]}df

cos[2πf(p-p0)x]df

(9)

由公式(9)发现,拉东谱能量在一定范围内,在以能量团中心为原点的坐标轴内对称分布,因此我们给出如公式(10)的能量聚焦滤波器作用在拉东谱上,即:

r(τ+τ′,p-p′)·r(τ-τ′,p+p′)·

r(τ+τ′,p+p′)dp′dτ′

(10)

式中:wt、wp分别表示τ、p方向窗的大小。由于公式(9)中拉东谱对称性成立的条件是在能量团中心点(t0,p0)附近,因此窗wt和wp的选取不能过大。能量聚焦滤波器filt(τ,p)作用在拉东谱上,能使拉东谱能量向能量团中心点(t0,p0)收敛,有效地提高了拉东谱的分辨率。

1.2.2 反射界面法线方向概率分布与角度域共成像点道集的生成

本文通过以下几个步骤获得地下反射界面法线方向概率分布:

1) 将逆时偏移成像剖面做线性拉东变换以获得拉东谱;

2) 将能量聚焦滤波器作用于拉东谱以得到高分辨率拉东谱;

3) 利用公式(11)计算地下各点反射界面法线方向概率分布。

(11)

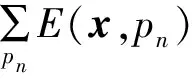
(12)

具体实现时,我们进行了3次波场重构。首先重构炮点正向波场,将炮点波场正向外推至时间最大值,在炮点波场正向外推的同时,实现:①保留边界波场,用于逆时重构炮点波场,以解决波场存储问题;②记录地下各点地震波主能量到达时并使用公式(4)计算主能量入射方向。然后同时逆时重构炮点和检波点波场,利用炮点波场正向外推时记录的地下各点主能量入射时间和计算的入射方向以及由公式(11)得到的地下反射界面法线方向概率分布,用公式(12)提取角度道集。

从方法的实现过程可以发现,本文方法在计算炮点波场主能量传播方向时不需要进行波场存储,因此对波场外推计算效率影响较小。与基于入射方向和反射方向获取角度域共成像点道集的方法相比,本文方法只增加了计算高分辨率拉东谱的工作量。

2 数值实验与分析

为了检验本文方法的正确性,采用带有一个高速岩体的二维鲸模型进行数值实验。模型大小601×201,网格间距为10m,如图1所示。图2是模型逆时偏移成像剖面。图3a为图2在x=3000m处的拉东谱。图3b为能量聚焦滤波器作用后的高分辨率拉东谱,可以看出,经能量聚焦滤波器作用后,拉东谱的性质发生了很大改变,能量团更集中,分辨率更高,能准确反映反射界面法线方向,为生成角度域共成像点道集提供了有效的基础数据。图4是采用3种不同方法提取的x=3000m处的角度道集,图4a是采用炮点波场和检波点波场分别计算入射方向和反射方向投影得到的角度域共成像点道集,张角范围为0～180°,间隔为1°;图4b是采用炮点波场计算入射方向、利用偏移剖面计算反射界面法线方向投影得到的角度域共成像点道集,半张角范围为0～90°,间隔为1°;图4c是采用本文方法得到的角度域共成像点道集,半张角范围为0～90°,间隔为1°。图5、图6和图7 分别是与图4中3种方法对应的浅层角度域共成像点道集。

图1 鲸速度模型

图2 逆时偏移成像剖面

图3 初始拉东谱(a)和能量聚焦后的拉东谱(b)

图4 采用不同方法得到的角度域共成像点道集a 基于ps,pr; b 基于ps,pn; c本文方法

不难看出,采用本文方法得到的角度域共成像点道集(图4c),明显好于基于ps,pr(图4a)或基于ps,pn(图4b)得到的角度域共成像点道集。由于通过检波点波场计算的坡印廷矢量不够稳定,使得投影得到的角度道集能量分布不连续,特别是由于边值条件不完备造成的绕射波在浅层发育明显,使得浅层能量投影不准确,严重影响角度道集(图5)的质量;而基于ps,pn得到的角度道集(图6)比基于ps,pr得到的角度道集(图5)有一定的改善,但是因为在无反射界面区域pn不存在,这直接导致了无反射界面区域能量投影不准确。本文方法用反射界面法线方向的概率分布替代pn,得到的角度域共成像点道集(图4c和图7)能够使有反射界面区域能量相干加强,无反射界面区域能量相互抵消,改善了道集的质量。

图5 采用基于ps,pr方法得到的浅层角度域共成像点道集

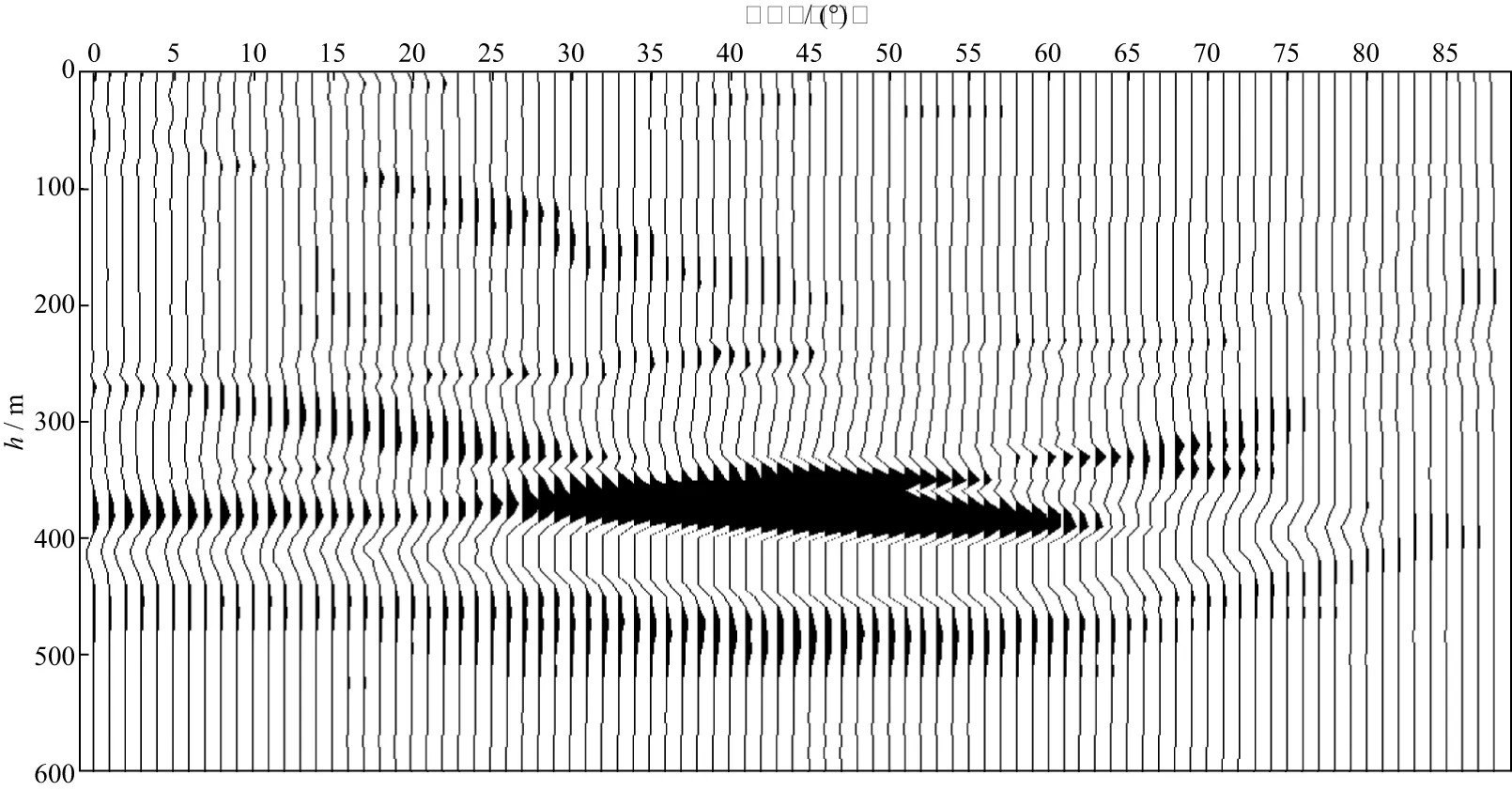
图6 采用基于ps, pn方法得到的浅层角度域共成像点道集

图7 采用本文方法得到的浅层角度域共成像点道集

3 结论与讨论

本文提出了一种能在消耗较少计算资源时就可以提高拉东谱分辨率的方法,并基于该高分辨率拉东谱获取了地下反射界面法线方向概率分布,用以替代单一的地下倾角值计算。提出了利用地下反射界面法线方向概率分布和入射波方向提取逆时偏移角度域共成像点道集的方法,使用该方法获得的道集相比于同类型基于坡印廷矢量类的角度域共成像点道集提取方法没有显著增加计算量和存储量,生成的道集在精度和噪声压制方面都有明显的提高。数值实验结果表明,采用该方法获得的角度道集能量投影更准确,道集更合理。从二维向三维拓展应用时,通过计算两个正交的二维反射界面法线方向概率分布,即可得到三维地下反射界面法线方向概率分布,进而得到三维角度域共成像点道集。