基于行波分解的绕射波成像方法研究

朱万怡,王华忠,吴成梁,徐 鹏

(波现象与智能反演成像研究组WPI,同济大学海洋与地球科学学院,上海200092)

2000年以来,随着国内外老油田的勘探程度逐步加深,油气地震勘探的目标发生了显著的变化,主要是由以横向缓变的层状介质为主的构造油气藏逐渐转向复杂、小尺度的构造油藏以及隐蔽油气藏。该类油气藏的勘探原则上需要一套新的思路,使得地震波偏移反演成像的结果满足岩性储层识别与解释的需求[1-3]。

地震勘探所面对的地下介质可以抽象为横向缓慢变化的广大沉积层中分布着由于火山活动、后期地质构造运动和其它地球动力运动所产生的小尺度速度异常体。断层、裂缝、地层尖灭、粗糙界面、孔洞等(大)小尺度的地质异常体是常见的油气运移通道和(或)储集体,对它们的刻画和描述是油气勘探的重要目标[4-5]。在常规的地震处理方法中,大部分算法都侧重于利用来自层状界面的反射数据,而来自反射界面以外的同相轴(比如绕射波)通常都被忽视。然而,绕射波数据中也包含着地下介质的丰富信息,对绕射波成像非常必要。早在20世纪50年代,诸多学者就认识到了绕射波在地震勘探中的重要性[6-7],KREY[6]指出绕射波是地下非均质地质体最直接的响应,使用绕射波信息可以提高地震资料处理的分辨率。但是由于绕射波能量往往比反射波能量弱很多,从而导致了即使将其偏移归位,通常也会被反射体所掩盖[8]。因此必须考虑如何单独对绕射波数据进行偏移成像,突出地下介质中的小尺度地质异常体。

根据绕射波和反射波在运动学和动力学特征上的差异,可以分别在数据域和成像域中利用两者的特征差异分离反射波与绕射波,从而实现对绕射波场单独成像的目的[9-10]。因此,绕射波成像方法主要分为:数据域绕射波成像方法与成像域绕射波成像方法。数据域中的分离方法有:基于绕射波旅行时方程构建绕射波时间剖面的D-Section分离方法[11-12];聚焦-反聚焦(Focusing-Defocusing)方法[8],其利用反射波具有固定镜像虚震源而绕射波在伪深度剖面上发散的特点,将聚焦的反射波切除再反聚焦从而在全波场中去除反射波;平面波域中的绕射波分离方法[13],其基本思想是在平面波入射的情况下,地下层状反射界面的地震记录为线形,而地下绕射点的地震记录为双曲形,利用滤波的方法滤去线性的反射波从而得到主要含绕射波成分的剖面;另一些数据域分离方法如CRS技术分离方法[14]及Multi-focusing方法[15],其实质为建立零偏移距剖面的方法。数据域中的分离方法大多基于射线理论,利用反射波与绕射波在传播旅行时上的不同特征进行分离,然而射线理论本身并不足以表达复杂地质条件下出现的波现象,因而这些方法在复杂介质情况下的适用性降低。成像域中的绕射波分离方法主要是在角度域成像中进行。根据反射能量集中在第一菲涅尔带而绕射能量较发散的特点,MOSER等[16]和KOZLOV[17]提出了修改Kirchhoff偏移积分公式中的加权函数从而压制反射波能量的反稳相绕射波成像方法,但由于其使用的是积分类偏移方法实现角度域成像,绕射波的收敛和聚焦效果都不如波动方程类的偏移方法。基于反射波和绕射波在倾角成像道集上的特征差异,许多学者提出在倾角成像道集中利用平面波滤波等方法分离绕射波并进行速度分析[18-21]。

由地下反射界面产生的反射波可以看成不同绕射点的绕射叠加过程,反射波与绕射波的区别在于反射波遵循Snell定律,具有方向性,而绕射波无方向性。因此可以根据地震波传播过程中的传播方向区分绕射波和反射波。在波场传播过程中分解不同方向的波场,并采用合适的成像条件提取绕射波进行成像是可行的,但是需要在每个波场外推过程中,进行波场分解提取对应的波场方向,计算量巨大,无法高效和精确地实现。为了避免波场外推中波场分解带来的计算量,可以分别将来自某一特定方向的地震波进行成像(例如可以分别对左行波和右行波进行成像)。根据绕射波和反射波的方向差异性,针对地下某一成像点,反射波只在满足Snell定律的方向上才能成像,而在其它方向上无法成像,但是绕射波在所有方向上均可成像。基于此,本文提出一种基于行波分解的绕射波逆时偏移成像方法,该方法首先利用解析时间波场外推及波场分解的方法,在逆时偏移的每一个时间片外推过程中得到震源端及检波点端的下左行波和下右行波,然后通过修改RTM零延迟相关成像条件,使用下左和下左行波相关、下右和下右行波相关,得到“正倾角反射层+绕射体”以及“负倾角反射层+绕射体”两种成像结果,最后将两种成像结果进行相关并得到最终的绕射波成像结果。该方法旨在较好地压制反射波能量,有效增强绕射波能量,实现绕射波成像的目的。最后利用数值实验和实际资料验证该方法的有效性。

1 行波分解理论

波场分解可通过傅里叶变换在频率-波数域实现[22-24]。利用傅里叶变换可以将地震波场分解为上下、左右行波,以震源端波场为例,关于时间和空间的傅里叶变换可表示为:

dtdxdz

(1)

式中:us表示震源端波场;Us是us的傅里叶变换形式。将震源端波场us和检波点端波场uR进行上、下行波分解[25-26]:

(2)

式中:上标up代表上行波,down代表下行波。在频率-波数域,震源端和检波点端的上、下行波可定义为[26]:

(3)

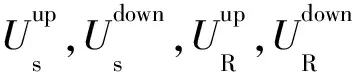
(4)

(5)

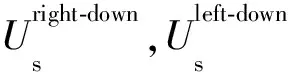
为了实现上述分解,需要对全波场进行高维傅里叶变换,因而需要巨大的计算量及存储量。另外一种有效的方法是采用希尔伯特变换构建解析波场[27-28],其实部为波场本身,虚部为波场在时间方向上的希尔伯特变换结果,在解析波场中仅包含正频率信息,因此可以通过空间波数的正、负来判断波场的方向。以震源端为例,震源端的解析波场为:

(6)

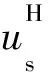
(7)

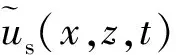
(8)

同理,检波点端波场的反传公式为[27]:

(9)

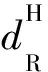
得到解析时间波场后,就可以在解析波场外推的每个时间层上进行空间傅里叶变换,将时间-空间域的波场转换到频率-波数域,从而利用(5)式来实现波场的下左和下右行波分量的分解了。图1为源检端下左、下右行波的分解结果,由图1可以看出,该方法可以较好地对波场进行下左和下右的方向分解。

图1 左、右行波分解结果a 原始波场快照; b 下左行波分解结果; c 下右行波分解结果

2 基于行波分解的绕射波逆时偏移成像方法

ZHANG等[30-31]提出在时间-空间域通过构建波场的希尔伯特变换对正、负倾角反射层分别进行成像,从而实现分离反射波、提取绕射波并对其单独成像的目的。该方法的核心思想是利用绕射波与反射波的方向性差异,在两次成像中,反射层只存在单一的成像剖面中,而绕射体在两次成像的剖面中都存在。由于该方法无法区分垂直向下传播的波场,在下左行波和下右行波分量中均含有垂直向下传播的波场,因此水平反射层会作为干扰留在绕射波成像结果中,并且该方法需要存储虚部波场,对硬盘存储和I/O均有较高的要求。本文提出通过构建解析时间波场,在时间-波数域通过傅里叶变换进行波场方向分解,并对分解的方向波场分别成像,然后将成像结果进行相关,从而实现绕射体成像的目的。该方法不需要存储虚部波场,并且可以灵活地选择波场方向范围,通过对波场传播角度的控制,消除垂直向下传播的波场,有效压制了水平反射层的干扰。

2.1 传统逆时偏移成像方法

逆时偏移(RTM)技术在20世纪80年代由MCMECHAN[22]、BAYSAL等[32-34]提出并取得了一系列的发展。基于波动理论的逆时偏移,由于其不受倾角和偏移孔径的限制,可以有效地处理纵横向剧烈变化的地球介质物性特征(如速度、密度等),是现行偏移方法中最精确的一种成像方法。传统的RTM零延时互相关成像条件公式可以表示为:

(10)

式中:nt代表时间采样点数;nshot为炮数;I为成像结果。直接采用(10)式作为成像条件会引起成像假象和低频噪声,为避免成像假象和低频噪声,LIU等[26]提出将波场进行上、下行波分解,利用震源端和检波点端同向传播的波场进行相关成像,成像条件变为:

=I1+I2

(11)

式中:I1为震源端下行波场与检波点端下行波场相关成像结果;I2为震源端上行波场与检波点端上行波场相关成像结果。在宏观速度纵向梯度较大,且存在高陡构造时,I2成像分量才有显著贡献,在不存在高陡构造的情况下,可以忽略震源端上行波和检波点端上行波相关成像的结果。因此,若只采用震源端下行波和检波点端下行波相关进行成像,则修改后的成像条件变为:

(12)

2.2 绕射波逆时偏移成像方法

绕射波是由于地下地质异常体的尺度小于地震波波长而产生的,绕射波与反射波在运动学特征上存在一定的差异,绕射波的能量通常比反射波低一到两个量级。如图2所示,反射波的传播符合Snell定律,即入射角等于反射角,地震波入射到反射体后,反射波只沿着符合Snell定律的方向发生反射,因此反射波具有方向特征。根据入射波场与反射波场的方向,可以计算反射层的倾角,相应地,特定的反射层的入射射线与反射射线的方向与该反射层的倾角有关。而绕射波的传播不符合Snell定律,地震波入射到绕射体后,绕射波会向各个方向出射,并由地面的检波器接收,绕射波的传播不具有方向特征。这一特征差异可被用于反射波和绕射波的分离成像。

图2 反射波(a)和绕射波(b)传播示意

将(12)式中的下行波分解成下左行波和下右行波,则(12)式可以写成:

(13)

式中:

(14)

(15)

(16)

(17)

其中,Irr为震源端下右行波和检波点端下右行波相关成像结果,如图3a所示;Ill为震源端下左行波和检波点端下左行波相关成像结果,如图3b所示;Irl为震源端下右行波和检波点端下左行波相关成像结果,Ilr为震源端下左行波和检波点端下右行波相关成像结果,如图3c所示。反射层可以根据法向向量方向分为正倾角与负倾角两种反射层,如图4所示,本文定义正倾角反射层为朝向地面的法向向量与向右的水平线夹角为锐角(0～90°)的反射层,负倾角反射层为朝向地面的法向向量与向右的水平线夹角为钝角(90°～180°)的反射层。

图5为正倾角反射层成像原理示意图。由图5可见,在震源端入射波场为下右行波的情况下,由几何关系可知,检波点端出射波场必定为下左行波(图5 中红色实线所示),也即不可能为下右行波,因此Irr的成像结果中没有正倾角反射层的像;在震源端波场为下左行波时,检波点端出射波场可能为下左行波(图5中绿色实线所示),因此Ill的成像结果中含有正倾角反射层的像。同理,Ill的成像结果中没有负倾角反射层的像,而Irr的成像结果中含有负倾角反射层的像。而绕射波由于不符合Snell定律,波场入射到绕射体上,绕射体向各个方向出射绕射波,因此绕射体在Irr、Ill中均成像。此时可以认为Ill代表了正倾角反射层和绕射体的像,Irr代表了负倾角反射层和绕射体的像,由于正、负倾角的反射层都只在Irr或Ill其中一项中成像,在另一项中不成像,而绕射体在两项中均可以成像,对两项结果进行相关,即可以将正、负倾角的反射层的像都去除,突出绕射体的像。具体的成像公式如下:

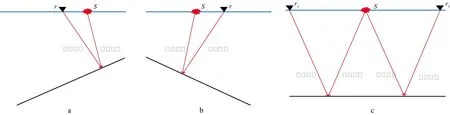
图3 不同方向行波相关成像示意a 震源端下右行波与检波点端下右行波相关成像; b 震源端下左行波与检波点端下左行波相关成像; c 震源端下左行波与检波点端下右行波相关成像以及震源端下右行波与检波点端下左行波相关成像

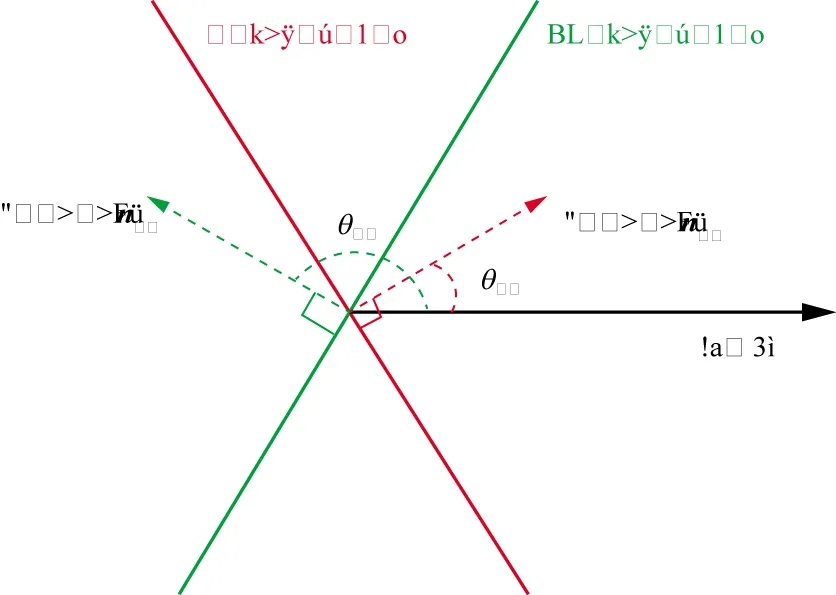
图4 正、负倾角反射层定义示意

Idiffraction=Irr·Ill

(18)

式中:Idiffraction为绕射波成像结果。

图5 正倾角反射层成像原理示意

在水平反射层或地层倾角较小的情况下,波场分解的过程中,由于垂直向下传播的波场既在下左行波分量中存在,也在下右行波分量中存在,因此水平反射层(包括小倾角反射层)既在正倾角反射层的像中存在,也在负倾角反射层的像中存在,利用(18)式无法压制水平反射层的能量。为了解决这一问题,在频率-波数域提取不同象限的波场进行波场分解时,可以在每个象限的边界处设置衰减窗函数,这样就可以灵活地分解得到特定角度范围的下左和下右行波分量。在下左和下右行波分量中都去除垂直向下传播的波场(以及沿小角度传播的波场),从而实现压制水平反射层(小倾角反射层)能量的目的,而去除一定角度范围的下左行波和下右行波分量对绕射波成像的影响很小。在时间-空间域通过卷积进行希尔伯特变换从而实现波场分解的方法无法去除沿特定角度范围传播的波场,因此选择利用傅里叶变换在频率-波数域实现波场分解对压制反射层的能量更加有效。

3 数值试验

3.1 模拟数据

首先采用“凹”形模型验证本文方法的有效性。图6a 为速度模型,该速度模型存在一个正倾角的反射层、一个负倾角的反射层以及4个绕射点;图6b为常规的RTM成像结果;图6c和图6d分别为Ill与Irr的成像结果,分别代表了“正倾角反射层+绕射体”的像和“负倾角反射层+绕射体”的像;图6e为利用本文方法得到的绕射体成像结果。对比图6c与图6d可见,在Ill的成像结果中只存在正倾角的反射层与绕射体的像,其中两个绕射体清晰可见,但依然有两个绕射体被正倾角反射层掩盖,难以有效识别;在Irr的成像结果中只存在负倾角的反射层与绕射体的像,与Ill的结果正好相反。因此利用公式(18)进行相关后可以有效压制反射层的像,增强绕射体的成像结果。

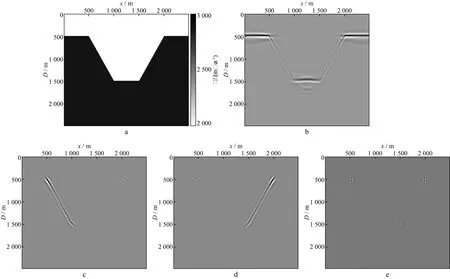
图6 “凹”形模型成像结果a 速度模型; b 常规偏移结果; c “正倾角反射层+绕射体”成像结果; d “负倾角反射层+绕射体”成像结果; e 绕射体成像结果

进一步地,为了验证复杂模型下本文方法的有效性,采用Sigsbee模型进行测试。图7a为Sigsbee偏移速度模型,速度模型以层状反射地层为主,并发育数组断层,此外,该模型还存在大量由粗糙界面引起的绕射点,第一炮在x=0处激发,共50炮;图7b为常规RTM成像结果;图7c和图7d分别为Ill与Irr成像结果;图7e为采用本文方法得到的成像结果。由图7可以看出,常规RTM成像中,绕射体被能量更强的反射界面掩盖,难以识别,而采用本文方法得到的结果,可以有效地对绕射体进行识别,并更加清晰地指示了断层的位置。为验证本文方法对速度误差的敏感性,采用不同的偏移速度模型进行成像,实验结果如图8所示。其中图8a为采用95%真实Sigsbee速度模型平滑之后的偏移速度模型;图8b为采用80%真实Sigsbee速度模型平滑之后的偏移速度模型。受偏移速度误差的影响,常规成像结果中成像位置发生变化,绕射体的成像不再聚焦,但采用本文方法仍然可以有效地压制反射波,较好地突出绕射波成像,识别绕射体的相对位置。

3.2 实际地震数据

采用某工区二维实际地震数据测试本文方法的有效性,该数据包含130炮,每炮间隔150m,时间采样为4s,采样间隔为0.5ms,双边观测,最大偏移距为1976m。图9a为实际地震资料常规逆时偏移成像结果;图9b为采用本文方法得到的绕射波成像结果。在浅层地区,反射波同相轴表现为水平层状,上、下反射界面分界明显,同相轴的分辨率较高。在横向位置1.0km和1.8km处出现了明显的断层,该断层延伸至深度1400m左右的不整合面上。从图9可以看出,在常规成像剖面中,断层和绕射体被掩盖掉,无法识别;而在本文方法的成像结果中,几乎没有连续的反射层的像存在,断层和绕射点可以清晰地识别。由于本文方法可以灵活地选择波场方向,不存在垂直向下传播的波场无法区分的问题,因此浅层地区的水平层状反射层几乎完全被去掉。实际资料应用结果说明了本文提出的绕射波成像方法的有效性。

图7 sigsbee模型成像结果a sigsbee速度模型; b 常规偏移成像结果; c 正倾角反射层+绕射体成像结果; d 负倾角反射层+绕射体成像结果; e 绕射体成像结果

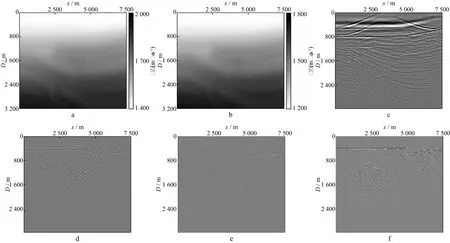
图8 不同速度误差下的成像结果a 减速5%的sigsbee速度模型; b 减速20%的sigsbee速度模型; c 图8a的常规成像结果; d 图8b的常规成像结果; e 图8a的绕射体成像结果; f 图8b的绕射体成像结果

图9 实际资料RTM成像结果(a)与绕射波成像结果(b)

4 结论与讨论

绕射波成像对油气勘探具有独特的价值,本文发展了一种基于波场方向分解理论的绕射波逆时偏移成像方法。该方法基于反射波和绕射波传播方向的特征差异,采用波场方向分解理论构建了针对绕射波成像的逆时偏移成像条件,最终实现了绕射波成像的目的。为了在逆时偏移过程中高效便利地进行波场方向分解,采用了基于解析时间波场方向分解的波场传播方法。基于波场方向分解成像条件获得“正倾角反射层+绕射体”及“负倾角反射层+绕射体”两种成像结果,基于绕射波传播角度特征,将二者进行相关处理获得绕射波成像结果。凹陷模型和复杂模型数据的测试表明本文方法能够很好地获取绕射波成像结果,模型中断点的成像清晰。同时,在速度存在一定误差的情况下,仍然可对绕射点的相对位置进行成像。本文方法在实际数据中的实验结果表明该方法能够很好地对断点及潜山顶界面不连续位置进行成像,体现出一定的实际应用潜力。

数值试验表明:本文方法在速度存在一定误差情况下仍能获取绕射点的相对位置成像结果,但其成像位置不准确。在实际数据处理中,为了精确定位绕射体,仍然需要高精度的偏移速度模型。本文方法仅使用下行波进行成像,与单程波偏移类似,对于缝洞较为发育的探区存在的多次绕射及多次波无法很好地利用,将该方法拓展到双程波的情况下是进一步研究的方向。此外,在波场方向分解中为了消除水平层的影响,去除了少量绕射波信息,也会对绕射波成像振幅存在一定的影响。对于复杂波场,如何准确估计其传播方向仍然值得进一步研究。

致谢:感谢中石油勘探开发研究院及西北分院、中海油研究院和湛江分公司、中国石化石油物探技术研究院和胜利油田分公司对波现象与智能反演成像研究组(WPI)研究工作的资助与支持。